基于H∞最优灵敏度的串级控制研究与应用
2016-04-27岳婷婷石红瑞曹南
岳婷婷,石红瑞,曹南
(东华大学 信息科学与技术学院,上海 201620)
基于H∞最优灵敏度的串级控制研究与应用
岳婷婷,石红瑞,曹南
(东华大学 信息科学与技术学院,上海 201620)
摘要:串级控制系统中,副回路采用内模控制器,可以快速、有效地消除二次干扰;主回路以最优灵敏度为设计指标,由H(∞)最优控制理论得到主控制器整定参数,并简化为标准的串级控制结构。将所设计的整定方法通过嵌入WinCC全局脚本文件,使用S7-300 PLC作为控制器,应用于“THJFCS-1型现场总线过程控制系统实验装置”,对双容水箱的液位进行控制。实验结果表明: 运用该算法有较快的响应速度,超调量较小,对设定值的跟踪表现也符合要求。
关键词:内模控制最优灵敏度串级控制系统神经网络
Study and Application of Cascade Control Based on H∞Infinity Optimal Sensitivity
Yue Tingting, Shi Hongrui, Cao Nan
(College of Information Science and Technology, Donghua University, Shanghai, 201620, China)
Abstracts: Quadric disturbance can be eliminated effectively and rapidly by using inner model controller in secondary loop in the designed cascade control system. Minimum sensitivity is used as the design objective in primary loop. Regulating parameters of primary controller can be obtained by H∞optimal control theory, and is simplified into standard cascade control structure. The proposed regulating method is applied to THJFCS-1 fieldbus system process control experimental device to control the liquid level of double-holding with embedded into global script of WinCC and using S7-300 PLC as controller. The experimental results show faster response speed and smaller overshoot can be obtained by using this algorithm. The set point tracking performance also meets the requirement.
Key words:internal model control; H(∞ )infinity optimal sensitivity; cascade control system; neural networks
在过程控制的发展过程中,前馈反馈控制、自适应控制、Smith预估器、神经网络控制、多变解耦控制以及串级控制等都是比较可行的能够满足生产要求的高级过程控制系统[1]。其中串级控制系统由于能有效地解决延迟时间较长、扰动变化剧烈以及非线性系统的控制问题而得到广泛的应用。
串级控制系统由2个回路组成,可以快速消除二次干扰的内部副回路,用来完成“粗调”的任务;可以改善输出效果的外部主回路,在控制过程中起着“细调”的作用,以确保最终的输出值达到预期的要求。对串级控制的参数整定以及改进已经成为国内外控制领域研究的热点。很多研究人员将先进的控制算法与串级控制结构相结合,可以有效地提高系统的性能和鲁棒性。
文献[2]提出了一种三自由度的串级控制设计结构,若要实现则需在原有标准串级结构上增加额外硬件开销,笔者在此基础上提出: 可以化为标准结构串级控制系统,从设定值跟综、负载扰动抑制和系统鲁棒性三个系统指标进行设计。设计的串级控制系统如图1所示。

图1 串级控制系统示意注: C1——主回路控制器;CIMC——副回路内模控制器;P1,P2——主、副控对象;D1,D2——主、副回路上的干扰;P2m——P2的模型
1控制器的设计
假设P1和P2均是实际过程控制中出现的最为广泛的具有时间延迟的一阶系统,即:
(1)
式中:K1,K2——增益;T1,T2——时间常数;τ1,τ2——延迟时间。对于e-τs这个时滞环节,采用一阶泰勒公式展开处理,即e-τs=1-τs。
1.1副回路控制器C2
将图1中的副回路简化为简单的单回路,如图2所示。

图2 副回路等效回路示意
图2中副回路控制器C2为
(2)

(3)
(4)
1.2主回路控制器C1
将图1的主回路简化成简单的单回路,如图3所示。
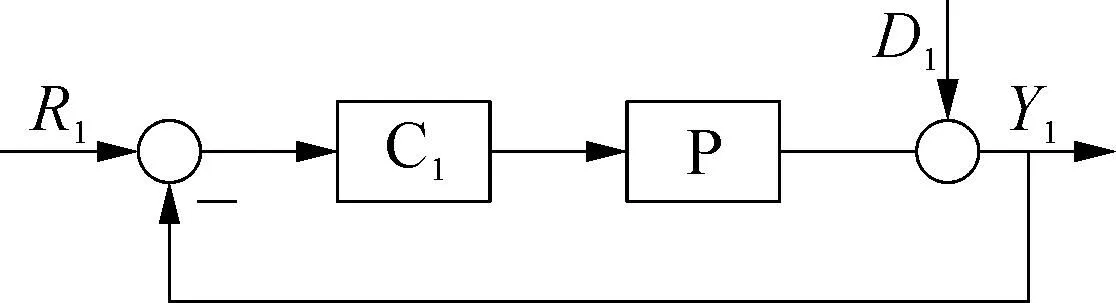
图3 主回路等效回路示意
由图1和图3可知:
P(s)=P1(s)P2(s)CIMC(s)=
(5)
经过IMC等效、化简为图4所示的框图。

图4 化简后的主回路结构示意
假设模型匹配,Pm(s)=P(s),根据图4可以得到:
(6)
(7)
定义灵敏度函数S(s)为
1-P(s)Q1(s)
(8)
将最优灵敏度min||W(s)S(s)||∞作为控制系统的设计指标,其中W(s)为权重函数,由于控制系统的输入通常为单位阶跃函数,则令W(s)=1/s[3],得到:
||W(s)S(s)||∞=
||W(s)(1-P(s)Q1(s))||∞≥
(9)
要想满足min||W(s)S(s)||∞,则需要W(s)(1-P(s)Q1(s))=τ1+τ2,得到:
(10)

(11)
(12)
2控制算法的实际应用
2.1系统建模
笔者采用S7-300 PLC,将PIW256和PIW258 2路模拟量输入连接到“THJFCS-1现场总线过程控制系统实验装置”的上、中2个水箱的液位传感器;PQW256模拟量输出调节电动调节阀开度[4]。
通过试验法建模可以得到水箱的数学模型:
(13)
根据上面控制器的推导公式可以得到C1(s)及C2(s)的传递函数:
(14)
其中α均取0.5。由于PLC内部的数据处理都是数字量,因而要对式(14)进行离散化。

带入参数得到:
C1(s)=53.864 0+0.261 8/s
(15)
采样周期取T=1s将式(15)离散化,可得到:
u(k)=u(k-1)+54.125 8e(k)-
53.864e(k-1)
(16)
同理,副控制器C2传递函数为
u(k)=u(k-1)+
72.4e(k)-72e(k-1)
(17)
2.2算法设计
SIMATIC WinCC6.0集成了脚本功能,通过全局脚本编辑器进行C语言编程,然后调用该函数。其算法设计流程如图5所示。

图5 算法设计流程示意
其中Avalue是由PLC在现场获得与WinCC进行数据传递的变量,而e2,e1,u1,u2会在下一次触发周期被刷新。
在文中,采样周期取T=1s,意味着在全局动作中添加一个周期为T=1s的触发信号,即每隔1s调用一次识算法。图6给出了中水箱液位随着时间变化的曲线图,其中液位设定值为10cm,初始时液位为0,系统超调量约为5%,上升时间约为200s,稳定时间约为260s。

图6 中水箱液位趋势曲线
3结束语
提出了一种基于内模控制和最优灵敏度的二自由度的控制器设计方法,以双容水箱为控制对象,将设计的控制算法嵌入到WinCC脚本函数中,利用WinCC与S7-300 PLC通信,将复杂的数学运算通过C项目函数来实现,提高了数据处理速度和算法效率。通过WinCC实时监控水箱的液位曲线,证明该算法在实际的水箱系统中有较快的响应速度,较小的超调量,实际控制效果明显。
参考文献:
[1]HANG C C, LOH A P, VASNANI V U. Relay Feedback Auto-tuning of Cascade Controllers[J]. IEEE Trans. on Control Syst. Tech., 1994, 2 (01): 42-45.
[2]尹成强,王洪涛.一种三自由度串级控制的仿真研究[J].计算机仿真,2012,29(01): 127-130.
[3]张卫东,徐晓鸣.典型不稳定时滞对象的基于最优灵敏度控制[J].上海交通大学学报,2001,35(09): 1303-1305.
[4]刘剑,奚邦庆,杨杰传.脚本在WinCC中的应用[J].中国高新技术企业,2010(27): 80-81.
[5]江春红.基于PLC的液位模糊控制系统设计[D].合肥: 合肥工业大学,2008.
[6]石红瑞,刘玺,刘勇,等.二次开发WinCC嵌入模糊控制算法[J].石油化工自动化,2002,38(01): 39-41.
[7]樊厉,林红权,高东杰.过程控制常用连续模型的直接辨识法与应用[M].控制工程,2006,13(04): 310-313.
[8]YONGHO L, SUNGOOL OH, SUNWON P. Enhanced Control with a General Cascade Control Structure[J]. Eng Chem Res, 2002, 41(11): 2679-2688.
[9]ALFARO V M, VILANOVA R, ARRIETA O. Robust Tuning of Two-Degree-of-Freedom (2-Dof) PI/PID based Cascade Control System[J]. Journal of Process Control, 2009, 19(10): 1658-1670.
中图分类号:TP273
文献标志码:B
文章编号:1007-7324(2016)01-0035-03
作者简介:岳婷婷(1992—),女,东华大学控制科学与工程专业在读硕士研究生,主要从事过程控制方面的研究。
稿件收到日期: 2015-09-13,修改稿收到日期: 2015-10-22。
