生物启发式算法求解多模态优化问题研究

钱乾，芮坤坤　(安徽商贸职业技术学院电子信息工程系，安徽 芜湖 241002)

程美英　(合肥工业大学管理学院，安徽 合肥 230009；南洋理工大学计算机工程学院，新加坡 639798)



生物启发式算法求解多模态优化问题研究

钱乾，芮坤坤(安徽商贸职业技术学院电子信息工程系，安徽 芜湖 241002)

程美英(合肥工业大学管理学院，安徽 合肥 230009；南洋理工大学计算机工程学院，新加坡 639798)

[摘要]实际生活及工程应用中的诸多问题均可归结为多模态优化问题，研究多模态优化问题的目的在于找出问题的所有全局极值解或有意义的局部极值解。从算法的“完全收敛性”出发，探讨了目前生物启发式算法(如遗传算法、蚁群算法、萤火虫算法、鱼群算法、粒子群算法等)求解多模态优化问题存在的问题和缺陷，并得出其在求解多模态优化问题时必须满足的条件：种群的多样性及种群分布的均匀性。随后概括并总结了目前求解多模态优化问题而保持种群多样性及均匀性的若干策略，着重研究了通过生物启发式算法并结合改进小生境技术在多模态优化问题求解中的研究进展，最后评述了今后一些有意义的研究方向及主要研究内容。

[关键词]多模态优化问题; 生物启发式算法；完全收敛性;小生境技术;种群多样性

多模态优化问题(Multi-Modal Optimization)或多峰函数优化问题(Multi-hump Function Optimization，MFO)[1]自提出至今，得到了众多学者的广泛关注。相对于解决其他形式的优化问题，求解多模态优化问题既要避免算法陷入局部极值解，又要让不同的极值解在种群中都有出现的机会，以便找到更多的优秀解。传统的解析方法或数值优化算法,如牛顿法、DFP变尺度法、梯度下降法、Hooke-Jeeves方法、混沌法以及改进的Powell方法等在目标函数较为简单或者说较少峰值的多模态优化问题中表现较好、求解精度较高，但对目标函数有较强的限制性要求、依赖初始值的选择、缺乏通用性以及求解时间难以忍受等缺陷限制了这些传统算法的广泛应用。生物启发式算法，如遗传算法、蚁群算法、粒子群算法、萤火虫算法等，因只需根据相应的启发式信息指导搜索方向，操作简单而受到学者的广泛研究。但易陷入局部最优(即算法的早熟收敛)、不能搜索到所有全局最优解(或局部最优解)等缺陷在上述启发式算法中依然存在。下面，笔者从多模态优化问题的数学模型和完全收敛性入手，探讨了近些年运用生物启发式算法求解多模态优化问题的若干策略以及今后的一些主要研究方向。

1多模态优化问题

问题描述如下：

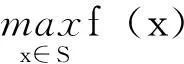
其中，x∈Rn称为时变量；S∈Rn称为参数搜索空间；f:S→R称为目标函数；S={x|x∈Rn;li≤xi≤ui,i=1,2,…,n}，通常S是一个n维长方体。

定义1设x*∈S，若存在δ>0，使得当x∈S且‖x-x*‖<δ时，总有f(x)≤f(x*)，则称x*为f在S上的局部极值解，f(x*)称为一个局部极值。

定义2 设存在x*∈S，使得对任意x∈S都有f(x)≤f(x*)，则称x*为f在S上的全局极值解，f(x*)称为一个全局极值。

定义3已知f*是f在S上的全局极值，若存在且仅存在一个x*∈S，使得f(x*)=f*，则称函数f(x)是一个单峰值函数。

定义4已知f*是f在S上的全局极值，若存在互不相同的x1,x2,…,xm∈S，使得f(xi)均为全局极值或局部极值，则称f(x)是一个多峰函数，也即多模态函数。

多模态优化问题(或多模态函数)是相对于单模态函数而言的，其目标旨在求出所有全局最优解或多个有意义的局部极值解。

2生物启发式算法求解多模态优化问题的完全收敛性

不同于单峰函数优化问题中涉及的“全局收敛”的概念,多模态优化算法的收敛性应理解为随着进化代数的增大,算法最终能够以概率1找到定义域内所有的极值解，称之为完全收敛(Complete Convergence)[2]。

定义5对于多峰函数f(x)，在定义域中共有m个峰，这m个峰的极值点分别记为φ1,φ2,…,φm，t代时的种群记为Z(t)，当且仅当：

(1)

则称算法是完全收敛的。

2.1遗传算法完全收敛性

遗传算法(Genetic Algorithm，GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，最初由美国Michigan大学J.Holland教授于1975年首次提出，并在同年，J.Holland提出了基于小生境的遗传算法这一思想，1987年Goldberg和Richardson基本实现了这一想法。文献[3]以马尔科夫链为分析工具，证明了基本小生境遗传算法不能停留在完全峰值状态中，即简单遗传算法不能完全收敛。

2.2蚁群算法完全收敛性

蚁群算法(Ant Colony Optimization, ACO)是一种用来在图中寻找优化路径的概率型算法，由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁寻找食物过程中发现最短路径的行为。因蚁群算法主要依靠信息素吸引其他的蚂蚁，随着算法的迭代，几乎所有的蚂蚁都会聚集到同一条路径上，这就使得ACO算法不适合求解多模态优化问题[4]，但此部分没有相关的理论证明。2006年熊伟清等[5]将二进制编码与ACO算法相结合，提出了二进制蚁群进化算法(BACO)，2009年严彬等[6]从理论上证明在BACO算法中，因蚂蚁每次只需从面前的2条路径进行选择，随着迭代次数的增加，蚂蚁几乎全部集中在其中一条路径上，即每次运行只能保证求解到问题的一个最优解，单一种群所对应的单一二元网络不能给出多模态优化问题的全部最优解。

2.3萤火虫算法完全收敛性

萤火虫算法(Glow warm Swarm Optimization, GSO)是由印度学者Krishnanand 和Ghose于2005年提出的一种模仿萤火虫群发光行为的群智能算法。在萤火虫算法中，每只萤火虫个体有不同的搜索范围，即决策域，每只萤火虫个体在决策域范围内朝比自身亮的萤火虫靠近，若感知范围内没有比自身优秀的个体，则停止不动，最终所有的萤火虫个体分别聚集在不同的全局(局部)极值点上[7]。

上述讨论的遗传算法、蚁群算法等的主要思想都是基于全局最优点和如何避免算法计算过程中种群多样性缺失速度太快的问题，人工萤火虫群优化算法在同时获得多模态函数的所有极值点的同时，可以不需要任何记忆，具有自由的梯度和不依赖任何全局信息等优点，是研究处理多峰函数优化问题的新方法[8]。2008年，Krishnanand和Ghose为特殊形式下的萤火虫群算法建立了理论基础，证明了每个子群的个体将分别收敛于所在子群的极值点，即完全收敛[9]。

此外，粒子群算法、鱼群算法等其他生物启发式算法在多模态优化问题上均有应用，如拉伸粒子群算法[10]、物种粒子群算法[11]、小生境粒子群算法[12]、小生境人工鱼群算法[13]及基于量子理论的小生境人工鱼群算法[14]等，但都没有在理论上对这些算法求解多模态优化问题的“完全收敛性”进行分析，这一部分有待于后续学者的完善。

3生物启发式算法与小生境技术相结合求解多模态优化问题

目前的多模态优化算法大多是基于生物启发式算法的多模态寻优过程。在用生物启发式算法求解多模态优化问题时，对群体的控制必须满足以下2点：①保持种群的多样性；②保持种群分布的均匀性。然而，绝大多数生物启发式算法本身的特性决定了其往往将精力集中在某一最有优势的优秀解上，只适用于搜索单一的全局最优解，当需要同时找到全局最优解或一些有意义的次优解时则显得无能为力。1917年Grinnell根据生物学中特定环境的组织功能衍生出小生境(niche)[15]的概念，在自然界中往往特征、性状相似的物种相聚在一起组成一个个小环境(子种群)，它们可以在种群内部繁殖，但不能和种群之外的个体繁殖。小生境技术的出现，为生物启发式算法求解多模态优化问题保持种群多样性提供了一种新颖的方法，而如何形成小生境则成为首要解决的问题。

3.1小生境的形成

在多模态优化问题中，每一个极值解可以看作一个小生境，子群体居住在小生境中参与竞争协作，因而小生境技术能使普通的优化算法具有发现多个最优解的能力，在很多领域的多模态优化问题中得到研究应用。实现小生境优化需要解决的2个重要问题是：①小生境的判断问题，即判断新发现的极值解是否与新产生的极值解属于同一小生境；②小生境保持问题，即如何将一些较优的不同小生境在后续的进化过程中稳定的保存下来。 纵观小生境的各种实现方法，其基本思想为：将连续的、无限的搜索空间划分为离散的、有限的小生境区域；在此基础上各种各样的小生境技术层出不穷。下面，笔者将介绍一些有代表性的小生境技术，为实际应用提供一些有效的参考设计依据。

图1　等区间分割小生境示意图

1)等分区间小生境生物在进化过程中之所以能形成千变万化物种，主要是因为物种有分化小种群的能力，各个小种群沿着不同的方向进化，逐渐分化成不同的物种。隔离主要是地理上的隔离，进而产生生殖、生态或行为上的隔离，由于隔离后的子群体彼此独立，因而对各子群体的控制相当灵活。

最简单的小生境技术是将整个搜索区间等分成几个小的子区间(或称小生境)，每个子区间相互隔离，独立进化，互不干涉(即互不交互信息)，最后综合各子区间的所得解，即为问题的所有最优解，如图1所示。基于区间分割的小生境技术又分各区间参数设置一致或不一致2种情形。

文献[16]将区间分割的小生境技术引入二元蚁群算法中，根据目标解的个数决定小生境的个数，若有m个解，则将搜索空间等分成m个子区间，每个子区间产生一个种群，各种群参数的设置完全一致，每个子种群并行独立搜索。仿真实验通过对Branin Rcos 函数(3个不同全局极小点)、six-hump camel back 函数(2个全局极小点)、shubert函数(18个全局极小点)进行测试，均能找到搜素空间的所有极值点。上述区间分割技术，一般来说，问题有多少个最优解，即设置相应数量的种群，但遗憾的是，在大多数实际问题中，事先并不知道解的数量和分布。叶青等[17]改进了上述问题空间的划分方法，针对一个具有n个自变量的多目标优化问题，将每一维自变量按其取值范围分割为d(d≥2)份，从而将问题空间划分成dn个子区域，d一般取值较小，以免时间代价过高。

基于区间分割的小生境技术在峰值较少的情况下基本能搜索到所有的极值解，但是事先必须知道解的大致分布和最优解的个数，这必然导致区域的划分不够灵活。

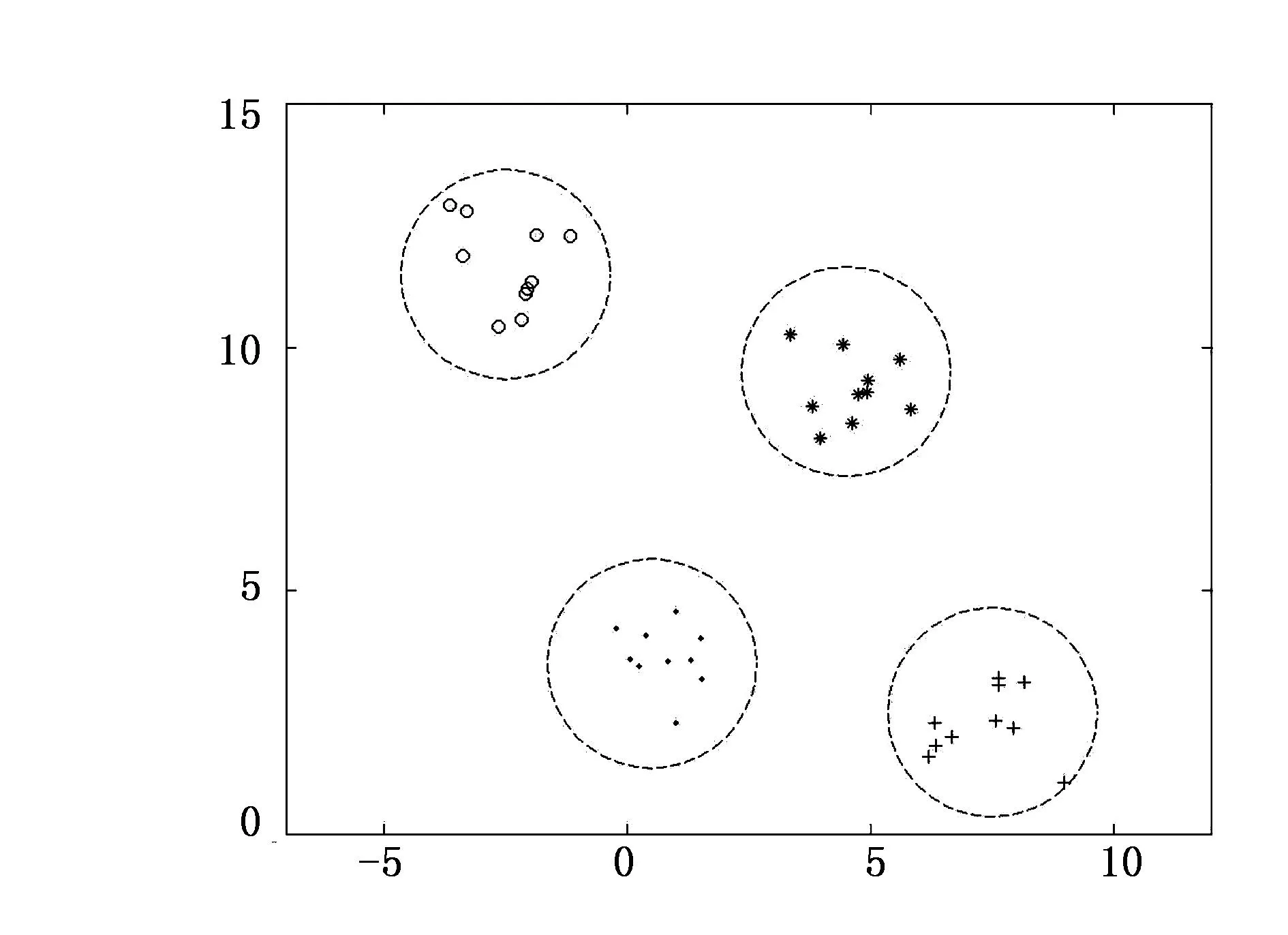
图2　聚类小生境示意图

2)聚类小生境采用上述等分区间的方式形成的小生境拓扑结构相对比较固定，但控制不够灵活，且初始解的分布不符合自然界“物以类聚，人以群分”的思想。随后研究者将数据挖掘中“聚类”的思想引入种群中，通过计算个体i,j之间的距离dij(如欧式距离、海明距离等)，若dij小于某一指定半径r，则这些个体归属同一类，处于同一个小生境中，最终形成一个个类似球体的超球面，如图2所示，称之为基于聚类分离的小生境形成技术。当然，上述等分区间的小生境属于基于聚类分离小生境的一种特例。

上述基于聚类的小生境空间划分方法被引入到多种启发式算法中，形成多个子种群(即小生境)，但是这种划分方法面临着一个重要的问题，即如何确定聚类的数目，而在算法的运行过程中自动确定聚类的数目是一个很困难的问题。文献[18]提出了一种基于适应度-距离相似度模型的概念(FDPSO)，打破了传统算法中只将个体之间的距离作为聚类的依据，而是将个体的适应度和距离相似度共同作为聚类的依据，使得具有更相近的适应度值和更近距离的2个个体属于同一个小生境的概率更高,也就是说,如果2个个体的适应度值相差很大,并且空间距离同样很大,那么这2个粒子很可能属于不同的小生境。通过对该算法的复杂度进行分析，FDPSO具有更低的计算量。

3.2生物启发式结合小生境技术求解多模态优化问题

目前生物启发式算法结合小生境技术求解多模态优化问题的主要代表为基于排挤模型的小生境技术和基于适应值共享的小生境技术以及后续学者在这2种模型上的若干改进。

1)适应值共享小生境技术及其改进1987年，Goldberg 和Richardson提出了一种基于适应值共享机制的小生境技术(SH: sharing fitness)[19],通过定义群体中个体的共享度,采用适应值非线性标度变换调整个体的适应值,使得群体同时保持多个高阶模式，其中小生境半径r是影响算法搜索性能的关键因素，该算法为了维持大量的小生境，必须有较大的种群规模，并且其中一部分小生境可能是无用的。随后，Petrowski等[20]提出一种特殊的适应值共享模型——清除模型，共享半径内的所有个体比较适应值，最佳的若干个体存活，其余死亡，清除模型的缺陷与上述适应值共享模型大体一致。

1993年，Beasley基于共享的小生境技术的不足，提出了序列小生境技术(sequential niching)，依次搜索多个全局最优解。其不足在于阻断了不同最优解位串之间模式信息的继承关系,交叉操作产生大量无效个体浪费计算资源,同时也存在着复杂的参数选择问题。

多模态优化问题一般存在多个局部极值解，局部极值解处适应值的大小很大程度上影响了它们被算法搜索到的概率。文献[21，22]通过分析基因池遗传算法的无限种群动力系统，从理论上证明了双峰函数局部极值解的适应值差与不动点之间的解析关系，并对该理论进行扩展，提出了适于求解多模态优化问题的两阶段遗传算法(FAGA)：对于一般的多模态函数,保持函数在某个阈值以下的各点的函数值不变,通过式(2)由拉伸效果的函数标度变换增大函数值在这个阈值以上的各点的适值差,就可以增加那些函数在阈值以上的局部极值解(包含全局最优解)的被搜索概率。相反，通过式(3)保持阈值以下的各点的函数值不变，通过有压缩效果的函数标度变换减小阈值以上的各点的适值差，减小那些阈值以上的局部极值解(含全局最优解)的被搜索概率，相应增加各阈值以下的局部极值解的被搜索概率。

假设变换前的原函数f(x)>0，若f(x)<0，先作如下处理：令f′(x)=f(x)+N，N≫max{0-f(x)}然后对f′(x)按式(2)、式(3)进行变换：

F1(f(x))=f(x) f(x)≤f(x')f(x)-1+T|f(x)-f(x')| f(x)>f(x'){

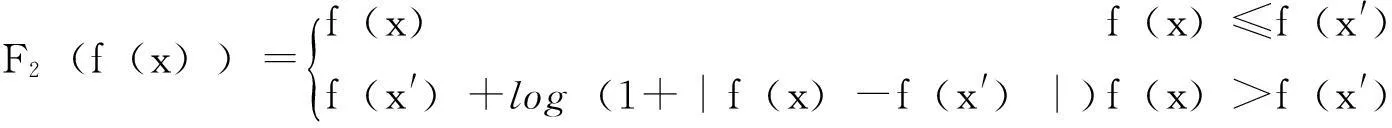
(2)

(3)

式中，F1(f(x))为具有拉伸效果的函数；F2(f(x))为具有压缩效果的函数。

通过对文献[22]中2个函数进行测试，结果明显优于PSO算法及基于小生境的适应值共享遗传算法。

2)排挤小生境技术及其改进1993年De Jong 提出的确定性排挤模型(deterministic crowding，DC)是一种维持群体多样性的选择方法[23,24]。在自然界中,当种群中的个体大量繁殖时,为争夺有限的生存资源,个体之间的竞争压力加大、个体消亡的概率升高、生存率下降。在采用DC模型时,新的子代个体仅仅替代与之相似的父代个体.然而,实验表明上述方法发现2个以上最优解的可能性极小[23,24]。 为此,在原有的基本操作方式的基础上,引入了概率排挤模型(PC: probabilistic crowding)[25],使之更加适合于多模态函数的求解。但是,仍然存在着已搜索到的最优解丢失的问题,而且CF参数(排挤系数)的选择与具体问题有关,很难事先确定合适的取值。

Harik借鉴联赛选择模型(tournament selection),提出了一种受约束的联赛保留策略，使得群体中构成以最优解点为核心的多个超球面小生境[26],对于给定的一类多模态函数的求解表现出了良好的性能。但是，需要事先指定各个小生境的核心、半径和数量,当不知道峰值点和峰距时,难以给定恰当参数。

文献[28]将混沌搜索、网络抑制、网络补充等机制相结合，提出了一种解决多峰函数优化的免疫混沌网络算法。该算法对一定数量的抗体进行混沌映射，产生混沌抗体群，将混沌抗体群中的抗体与父本比较，保留亲和度最高的抗体组成新抗体群，新抗体群组成免疫网络，通过混沌搜索不断提高抗体亲和度，当抗体群的平均亲和度无法提高时，利用抑制阈值消除相似抗体，其余保存在记忆池中。为了防止多峰函数的峰值大于预设的种群规模，需补充新抗体以调节种群的数量，如此循环迭代，直到整个网络达到动态平衡，最后记忆池中的抗体即为多峰函数的优化解。

文献[29]提出了一种基于隔离机制的动态小生境技术。该算法将初始群体分割成几个子群体，各子群体彼此独立，界限分明，子群体的规模同种群个体平均适应值相关，子群体平均适应值越高，则群体规模越大，并通过引入子群最大允许规模Smax、子群体最小生存规模Smin、幼弱保护政策、同种互斥以及新老更替政策等来保持种群的动态多样性。上述的这种小生境策略不仅使得子群体进化操作具有灵活性，子群体之间的相互竞争排挤给全局搜索具有导向性，且妥善解决了局部搜索和全局搜索的平衡。文献[6,30]分别将具有这种隔离机制的小生境技术应用于遗传算法、二元蚁群算法中，较好地应用于50个城市的TSP问题、多峰函数优化以及多重0/1背包选择问题。

文献[31]通过对克隆选择算法中记忆算子、抑制算子、重组算子等进行改进，并结合小生境技术，提出了一种求解多峰函数的小生境克隆选择算法。算法主要思想：随机产生N个抗体组成初始抗体群，对每个抗体计算其抗体-抗原亲和度，将抗体的亲和度评价值大于记忆阈值δn的抗体通过记忆算子添加到记忆库中(可防止在进化过程中优秀解被破坏)，并对其进行抑制算子操作；应用小生境适应值共享函数对初始抗体群中抗体的抗体-抗原亲和度进行调整(可以保证高、低峰同时被选中)；根据调整后的抗体-抗原亲和度，对每一个抗体进行克隆扩增和重组变异(包括抗体交换算子、抗体逆转算子、抗体移位算子，如图3～图5所示)，从而形成N个子抗体群；计算克隆扩增和重组变异后的抗体亲和度，从每个子群里选出一个最优抗体组成新的抗体群。此外，为了在整个搜索区域大幅度寻找抗体，随机生成 个新的抗体，替换新的抗体群中Ns个具有低亲和度的抗体。

图3　抗体交换算子　　　　　　　　　　图4　抗体逆转算子　　　　　　　　　图5　抗体移位算子

文献[32]受免疫系统中的记忆细胞机制启发，提出了免疫记忆策略。具体方法是：设计一个记忆算子，当种群中有优秀个体适应值超过一定阈值(称为记忆阈值)时，就迁移到记忆子群中；一旦个体迁移到记忆子群后，就删除原种群中与其相同的个体，然后再检查种群中是否还有优秀个体，如有则继续迁移，否则停止记忆操作。在记忆操作停止之后，检查种群中的个体数，如果小于原种群规模，则用随机产生的新个体补满，记忆子群中，一旦有新的优秀个体进入记忆子群，立即对该个体进行梯度进化,如Adaptive gradient descent(自适应梯度下降法)、Simulated Annealing(模拟退火)等，直到该个体到达所在的峰。然后，用进化完毕的个体与临时子群的其他个体逐一比较，去掉与之相似度大于一定阈值的个体(称为“相似性抑制”)，从而保持种群的多样性。

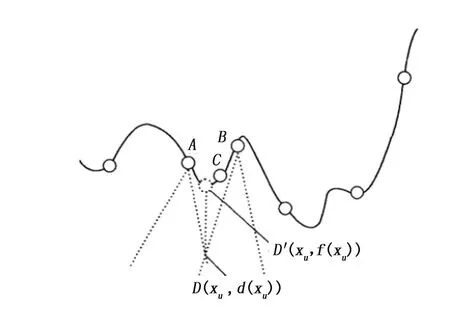
图6　基于局部抽象凸支撑面个体更新过程

邓勇军等[33]针对小生境半径难以确定及确定性算法复杂度高的缺陷，提出了一种提出了一种基于局部抽象凸支撑面的多模态优化算法(LAC)。在传统进化算法的框架下, 将目标优化问题转换为单位单纯形约束条件下的严格递增射线凸松弛问题。在更新环节利用新产生个体邻域信息构建下界低估支撑面, 通过引入主导个体思想, 寻找主导个体所属的支撑向量, 并利用该支撑向量的下降方向指导新个体更加高效的替换现有种群个体, 并减少替换误差, 避免出现早熟现象, 从而产生质量更高的新个体。假设C是一个trail个体(见图6)，寻找种群中离C最近的个体A，B，构建下界支撑面，得到下界函数极值点D(xu,d(xu))，若C在B主导的支撑面上，则B为主导个体，且C的适应值优于B，C取代B，循环此过程，完成一次种群的更新过程。

由上述可知：①基于空间分离的小生境技术必须对生物启发式算法的搜索行为施加必要的限制，通过定义搜索空间上的某种度量保持群体的多样性，并在群体中同时保留多个高适应值的高阶模式，防止某个高适应值的个体快速充满整个群体，使得优化算法可以搜索到多个全局最优解和局部最优解。②隔离机制的采用,使得种群中的个体被完全分隔成几个子群体,各子群体相互独立并行进化,不仅妥善地解决了局部搜索能力和全局搜索能力的矛盾,而且各子群体在整个进化过程中实际在不停的移动,最终遍历整个搜索空间,收敛在所有全局最优解上。

3.3小生境半径的选择

每个小生境由质心θ和半径r确定。以多峰函数为例，每一个峰所在区域是最准确、最合适的小生境范围，但是多峰函数的峰具有不同的高度、形状和面积，采用小生境技术时半径的设定是一个难点。

在种群的进化过程中，θ和r处于不断变化的状态。 r较大，有利于保持种群多样性，但进化速度缓慢；r较小，可加快算法的收敛速度，但种群多样性降低，算法容易陷入局部最优。在传统的小生境技术中，一般事先确定小生境半径r，这在实际问题中往往难以准确估计，并且若在进化过程中将各小生境半径设定统一值，往往会导致进化效果不佳。文献[34]根据种群适应度地形信息确定θ和r；Cho等[35]提出了一种种群规模和小生境半径r均可自动调整的小生境技术，在电机设计优化问题中得到了较好的应用；Dilettoso和Salerno等[36]提出了一种能够动态识别小生境和小生境半径技术，较好应用于电磁转杯设计优化问题中。文献[18]将粒子群算法中每个粒子在每一代找到与自己距离最近的粒子，并记录下这个最近距离,然后求出这个最近距离的平均值作为小生境半径r。

上述方法虽然能动态计算小生境半径，但计算方法相当复杂。文献[37]将“熵”的概念引入基于共享机制的小生境中，根据当前种群个体间的平均距离对半径r作自适应性调整。文献[38]针对多目标优化问题，在Pareto边界生成一颗最小生成树，将最小生成树的平均边长作为小生境半径。

然而，在小生境的生成过程中，存在某一个别个体，它不属于任何一个小生境，但其本质是单独存在的峰值，由于个体分布的不均匀，导致该个体周围缺乏邻居而不能构成一个单独的小生境，并且在划分小生境的过程中，还可能出现小生境半径r的交叉。为此，文献[39]引入标记策略，只采用小生境中心点和附近个体的距离信息描述函数的峰值形状，使得小生境划分更加准确,提高了小生境的划分效率,避免出现了无法划分的个体。

4生物启发式算法求解多模态优化问题的其他策略

多目标优化问题因存在多个相互冲突的目标，故其解为一组Pareto最优解集，因而多目标优化问题也可视为多模态优化问题。文献[40]通过目标空间变换方法，采用Pareto 前端在被称为平行格坐标系统的新目标空间中的分布熵及差熵评估种群的多样性及进化状态，并以此为反馈信息来设计进化策略,使得算法能够兼顾近似Pareto 前端的收敛性和多样性。同时,引入格占优和格距离密度的概念来评估Pareto 最优解的个体环境适应度,以此建立外部档案更新方法和全局最优解选择机制，最终形成了基于Pareto 熵的多目标粒子群优化算法。

文献[41]在DE(差分)群体进化算法基础上，利用群体中更新个体适应度信息构建多模态目标函数的广义凸下界估计模型，并对群体进行拓扑分类，综合考虑上下界偏差值提出一种表示种群拥挤程度的生境指标，从而保证形成协同进化的种群，进一步采用拓扑区域进化树更新策略来保证生境内部的局部搜索能力，仿真试验表明，该算法能够发现所有的全局最优解以及一些有意义的局部最优解。

近年来，还有众多学者融合多种策略求解多模态优化问题，吴建辉等结合Powell算法、免疫算法多子种群、协同进化、免疫优化、自适应杂交算子及邻域内非均匀变异算子及粒子群算法等众多策略,提出了2种解决多模态优化问题的3种新方法：合作-竞争多子种群粒子群免疫协同进化算法(MAPCPSOI)；基于串联混合方式的免疫云粒子群优化算法(PPSO)；基于串联混合方式的融合Powell搜索算法的粒子群优化算法(IPSO-P)等等[42～47]。

5总结与展望

工程及数学上的许多优化问题实质上均可归结为多模态优化问题(或多峰优化问题)，多模态问题进行多次优化技术，直到发现解的个数等于指定个数为止，然而多次优化并不能保证每次都收敛在不同的最优解上。笔者从小生境技术、种群多样性的保持等方面对多模态优化问题的求解策略进行综述，在研究过程中得出以下结论：

1)采用生物启发式算法求解多模态优化问题，重点在于保持种群的多样性和均匀分布，因而不管是采用小生境技术，还是采取其他策略，其最终的目的都必须对种群中的个体施加必要的策略，通过定义搜索空间中的某种度量来保持群体的多样性，并在群体中同时保留多个高适应值的高阶模式,防止某个高适应值的个体快速充满整个群体,使得算法可以搜索到多个全局最优解和局部最优解；

2)为了保证在算法迭代过程中优秀解不被破坏，在种群迭代过程中，需要采用相应的“记忆”机制，来保留进化过程中找到的最优个体；

3)不管是适应值共享小生境技术还是排挤小生境技术，它们之间其实并没有明显的界限，有时候可以相互交叉使用。

在研究的过程中，笔者发现以下有趣且尚待解决的问题：

1)因多模态优化问题的目的在于找出问题的所有全局最优解或多个有意义的局部最优解，小生境技术或多个种群的引入，实则具有隐含的并行性，如何将并行机制引入到多模态优化问题的求解过程中，势必能在很大程度上减少算法的运行时间；

2)目前的算法主要侧重于问题的应用，而相应算法的理论分析，尤其是算法的“完全收敛性”分析则研究并不多；

3)在实际应用过程，过度地将保持种群多样性的重任寄托在“小生境”身上，或者说小生境旧模型的改进或新模型的提出有时仍无法保证算法同时找到全部极值解，若让进化算法分担一部分保持种群多样性的任务，保证多模态优化算法整体运行的有效性，也是亟待解决的问题；

4)根据协同进化的理论，竞争和协作不仅存在于个体和个体之间，各子群体之间同样也存在着竞争和协作的关系，这也在一定程度上保持了种群的多样性,同时，个体的选择行为存在个体理性，群体的选择行为具有集体理性，如何实现各不同小生境之间的相互协作，实现信息交流，也是一个值得研究的问题；

5)目前对算法性能的测试主要是函数的应用，如何将企业、生产管理中的诸多问题抽象成多模态优化问题，以便给企业的生成管理提供多套备选方案，也是下一步准备研究的议题。

[参考文献]

[1]Basak A，Das S，Tan K C. Multimodal Optimization Using a Biobjective Differential Evolution Algorithm Enhanced With Mean Distance-Based Selection[J]. IEEE Transactions on Evolutionary Computation, 2013,17：666～685.

[2]杨孔雨,王秀峰.免疫记忆遗传算法完全收敛性研究[J].计算机工程与应用,2005,41(12):47～50.

[3]林焰,郝聚民,纪卓尚,等. 隔离小生境遗传算法研究[J].系统工程学报,2000,15(1) :86～91.

[4]Meng X Y, Huang S. A new method to design section area curve of ship based on niche ACO[A].Proc of the 8th World congress on Intelligent Control and Automation[C]. 2010:3230～3235.

[5]熊伟清，魏平.二进制蚁群进化算法[J].自动化学报，2007，33(3)：259～264.

[6]严彬,熊伟清,程美英,等. 带拥塞控制的多种群二元蚁群算法[J].控制理论与应用,2009,26(4):387～394.

[7]倪志伟，肖宏旺，伍章俊，等. 基于改进离散型萤火虫群优化算法和分形维数的属性选择方法[J]. 模式识别与人工智能, 2013, 26(12): 1169～1178.

[8]Krishnanand K N, Ghose D. Multimodal function optimization using a glowworm metaphor with applications to collective robotics [A].Proceedings of the Second Indian International Conference on Artificial Intelligence[C]. 2005: 328～346.

[9] Krishnanand K N, Ghose D. Theoretical foundations for rendezvous of glowworm-inspired agent swarms at multiple locations[J]. Robotics and Autonomous systems, 2008:549～569.

[10]Parsopoulos K E, Vrahatis M N.On the computation of all global minimizers through particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004,8:211～224.

[11]Li X.Adaptively choosing neighborhood bests using species in a particle swarm optimizer for multimodal function optimization[J].Proceedings of Genetic and Evolutionary Computing, 2004, 3102:105～116.

[12] Brits A, van den Bergh F.A niching particle swarm optimizer[A].Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution Learning[C].2002：692～696.

[13]张梅凤,邵诚.多峰函数优化的生境人工鱼群算法[J].控制理论与应用, 2008,25(4):773～776.

[14]江铭炎, 袁东风. 人工鱼群算法及其应用[M].北京：科学出版社,2012.

[15]Wessing S,PreussM,Rudolph G. Niching by multiobjectivization with neighbor information: Trade-offs and benefits[A]. IEEE Congress on Evolutionary Computation (CEC), 2013: 103～110.

[16]王柳毅，熊伟清.并行二进制蚁群算法的多峰函数优化[J].计算机工程与应用，2006,22(4)：42～45.

[17]叶青，熊伟清,江宝钏. 基于二元蚁群算法的多目标订单分配问题求解[J].计算机工程,2011,37(3):175～182.

[18]吕明伟.基于相似度模型的多模态粒子群优化算法研究[D]. 大连:大连理工大学,2013.

[19]吕佳，熊忠阳.面向多模态函数优化的混沌免疫网络算法研究[J]. 计算机应用，2006, 26(2)：456～459.

[20]Petrowski A. A clearing Procedure as a niching method for genetic algorithms[A].Proeeedings of the IEEE Conference on Evolutionary Computation [C].1996:798～803.

[21]李航,李敏强,寇纪松.遗传算法求解多模态优化问题的动力性[J].自动化学报,2008,34(2):180～187.

[22]李敏强,寇纪松, 林丹, 等. 遗传算法的基本理论与应用[M]. 北京:科学出版社,2002.

[23] De Jong K A. Genetic algorithm s: A 25 year perspective[A]. In: Proceedings of the Fifth International Conference on Genetic Algorithms[C].C A: Morgan Kaufmann Publishers, 1993.

[24] Mahfoud S W. Crowding and p re-selection revisited[A]. Manner R, M anderick B (eds.).Parallel Problem Solving from Nature [C] . Berlin: Springer, 1992: 67～76.

[25] Meng S O J, Goldberg D E. Probabilistic crow ding: Deterministic crowding with probabilistic replacement[A]. Ban Z W et al. (eds.).Proceedings of th e Genetic and Evolutionary Computation Conference 1999 (GECCO-99)[C] . C A: Morgan Kaufmann, 1999:173～179.

[26]Harik G. Finding multi-modal solutions using restricted tournament selection[A].Eshelman L J. Proceedings of the sixth International conference on Genetic Algorithms (ICGA 6)[C]. CA:Morgan Kaufmann,1995:24～31.

[27]谭竹梅,余晓峰,郭观七.排挤小生态遗传算法的改进方法[J].控制理论与应用,2004,21(4):65～654.

[28]薛文涛,吴晓蓓,单梁.多峰函数优化的免疫混沌网络算法[J].系统仿真学报,2012,22(4):915～920.

[29]王巍,彭力. 嵌入隔离小生境技术的混沌粒子群算法[J].系统工程与电子技术,2008,30(6):1151～1154.

[30]严彬. 多种群蚁群优化算法的研究[D]. 宁波:宁波大学,2009.

[31]叶文,欧阳中辉,朱爱红,等.求解多峰函数优化的小生境克隆选择算法[J]. 系统工程与电子技术,2012,32(5):1100～1104.

[32]郑士芹,王秀峰.基于多模态函数优化的改进克隆选择算法[J].计算机工程与应用,2006,42(3): 15～20.

[33]邓勇跃,张贵军.基于局部抽象凸支撑面的多模态优化算法[J].控制理论与应用.2014,31(4):458～466.

[34]Liu C Y,Wu W H. Niche identification techniques in multimodal genetic search with sharing scheme[J]. Advances in Engineering Software,2002,33:779～791.

[35] Cho D H, Kim J K, Jung H K. Optimal design of permanent-magnet motor using autotuning niching genetic algorithm[J]. IEEE Transactions on Magnetics, 2003,39(3):1265～1268.

[36]Diletoso E, Salerno N. A self-adaptive niching genetic algorithm for multimodal optimization of electromagnetic devices[J]. IEEE Transactions on Magnetics,2006,42(4):1203～1206.

[37]郑金华,刘磊,刘盼,等. 一种自适应小生境分布性保持策略[J].电子学报,2012,40(11):2330～2335.

[38]梁昌勇,陆青,杨善林,等. 一种基于小生境熵的自适应混合遗传算法[J].中国管理科学,2008,16(2):115～121.

[39]陈彦龙，张培林，李胜，等. 面向多峰函数的自适应小生境量子进化算法[J].系统工程与电子技术,2014,36(2):404～408.

[40]胡旺, Gary G, 张鑫.基于Pareto熵的多目标粒子群算法[J].软件学报，2014,25(5)：1025～1050.

[41]张贵军,何样军,郭海锋,等. 基于广义凸下界估计的多模态差分进化算法[J].软件学报,2013,24(6):1177～1195.

[42]吴建辉. 混合免疫优化理论与算法及其应用研究[D]. 湖南大学博士学位论文,2013.

[43]吴建辉,章兢,李仁发,等.多子种群微粒群免疫算法及其在函数优化中应用[J].计算机研究与发展,2012,49(9):1883～1898.

[44]李敏强,寇纪松.多模态函数优化的协同多群体遗传算法[J].自动化学报,2002,28(4):497～504.

[45]于歆杰,王赞基.自适应调整峰半径的适应值共享遗传算法[J].自动化学报,2002,28(5):816～820.

[46]王湘中,喻寿益.多模态函数优化的多种群进化策略[J].控制与决策,2006,21(3):285～288.

[47]毕晓君，王艳娇.用于多峰函数优化的小生境人工蜂群算法[J].系统工程与电子技术，2011，33(11)：2564～2567.

[编辑]张涛

[文献标志码]A

[文章编号]1673-1409(2016)07-0040-09

[中图分类号]O224

[作者简介]钱乾(1983-)，男，硕士，讲师，现主要从事群智能算法、数据挖掘方面的教学与研究工作; E-mail:sparkqq@126.com。

[基金项目]安徽省教育厅自然科学研究项目(KJ2013Z089)；安徽省教育厅自然科学研究重点项目(KJ2015A373)；安徽省教育厅质量工程项目(2014zy117)。

[收稿日期]2015-10-17

[引著格式]钱乾，芮坤坤，程美英.生物启发式算法求解多模态优化问题研究[J].长江大学学报(自科版)，2016,13(7)：40～48.