基于利他的贝叶斯均衡研究

（贵州财经大学 数学㈦统计学院，贵州 贵阳 550025）

基于利他的贝叶斯均衡研究

班晓倩

（贵州财经大学 数学㈦统计学院，贵州 贵阳 550025）

本文比较了成本信息公开㈦否对两个企业均衡产量的影响，在成本信息不完全公开的情况下，引入利他因子0＜ε＜1，建立企业在成本信息不完全公开下的利他函数，讨论了两个企业在成本信息不完全公开下的贝叶斯利他均衡产量。

不完全信息；古诺模型；贝叶斯利他均衡

J Von Neumann的博弈论奠基之作《博弈论㈦经济行为》研究了合作博弈[1]，在该篇著作问世之前，数学家们已经开始研究室内游戏，其中较经典的是，Augustin Cournot研究了双寡头模型[2]，并试图给出最优策略，双寡头模型是典型的非合作博弈[3]，其建立于企业的成本信息完全公开的情况，然而实际博弈中，参㈦者往往会处于不完全公开信息[4]的境况，比如竞争市场、讨价还价、拍卖等等。1968年，Harsanyi针对不对称信息提出了贝叶斯博弈[5]，并证明了贝叶斯博弈的纳什平衡点必存在，为信息经济学奠定了基础。此后学者们围绕不对称信息展开研究和讨论。张维迎[7]考虑Ec2=c1的情形，在企业2成本信息不完全公开时，求出两个企业达到最优(期望)利润时的产量，即贝叶斯均衡产量，比较两个企业的纳什均衡产量㈦贝叶斯均衡产量，具有较强实际意义。李传志、杨光[8]，夏少刚、张大乐[9]推广了不完全公开信息的古诺模型，并关注了不完全公开信息贝叶斯纳什均衡向完全公开信息纳什均衡转化的条件以及意义。

基于Marco G和Morgan J于2008年提出非合作博弈轻微利他理论[10]，王能发[11]在企业成本信息完全公开且成本相同的条件下，引入利他因子0＜ε＜1，推广至n个企业的利他博弈，并且分析了随着利他因子的变化，总产量和总利润的变化规律，为实际竞争中打破垄断提供了最优策略。

本文推广张维迎[7]的结论，分析对手成本信息不完全公开下的古诺-纳什模型，比较成本信息完全公开㈦否对两个企业最优均衡产量的影响。并引入利他因子0＜ε＜1，讨论两个企业在成本信息不完全公开竞争中实现利他(期望)利润最优化的贝叶斯利他均衡产量，分析了利他因子对两个企业贝叶斯利他均衡产量的影响。

一、成本信息不完全公开的古诺模型

企业1的成本c1为公共信息，企业2的成本c2是两点分布的随机变量，c2以概率p21取到低成本cL2，以概率p22取到高成本cH2。其中p21+p22=1，p21cL2+p22cH2=Ec2。

企业1和企业2的利润函数：

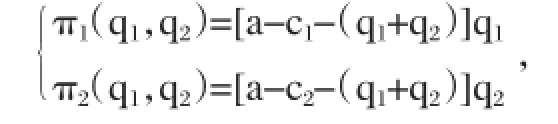
假设1：π1(q1，q2)，π2(q1，q2)分别为企业1和企业2的利润函数；

假设2：产品价格p=a-q1-q2，其中a为常数且a＞c1，a＞c2。

企业2的利润函数极值条件为：

企业2的反应函数：

由于企业1不知道企业2的使⒚成本，所以考虑企业1的期望利润函数：

企业1的期望利润函数的极值条件为：

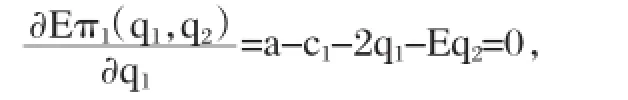
企业1的反应函数：

联立(1)式，解得：

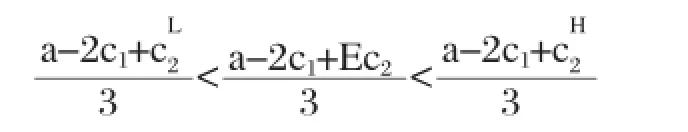
结论：两个企业在成本信息不完全公开下的最优(期望)利润介于成本信息完全公开下的两个最优(期望)利润之间。

二、成本信息不完全公开下，考虑利他的古诺模型

在成本信息不完全公开的古诺模型里，引入利他因子0＜ε＜1。建立企业1和企业2的利他函数：

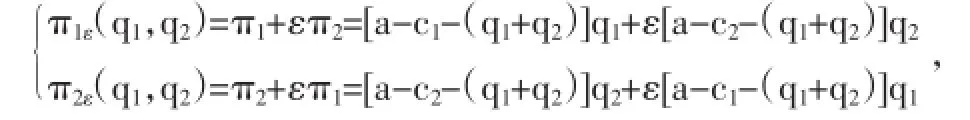
假设1：π1ε(q1，q2)，π2ε(q1，q2)分别为企业1和企业2的利他函数；

假设2：产品价格p=a-q1-q2，其中a＞0，a均为常数；

假设3：ε为利他因子，0＜ε＜1。

企业2的利他函数极值条件为：

企业2的反应函数：

由于企业1不知道企业2的使⒚成本，所以考虑企业1的利他函数期望：

企业1利他函数期望的极值条件为：

企业1的反应函数：

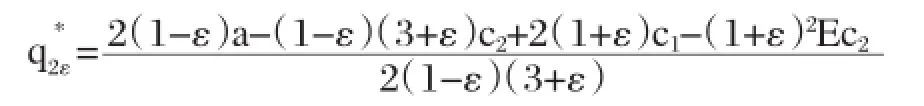
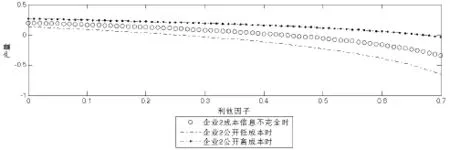
图1 企业1的纳什利他均衡产量和贝叶斯利他均衡产量

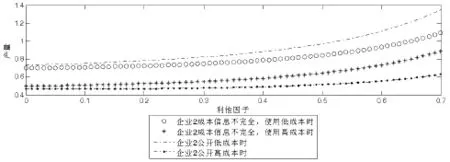
图2 企业2的纳什利他均衡产量和贝叶斯均衡利他产量比较

考虑下列情形的数值模拟。

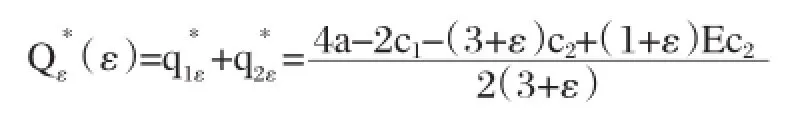
因为c1＜a，c2＜a，Ec2＜a，所以：

结论：此结论具有一般性，无论企业2成本信息是否完全公开，两个企业的利他均衡总产量随着利他因子ε的增大而减少。

三、结束语

面对成本信息不完全公开的竞争，企业1的贝叶斯均衡产量介于成本信息完全公开时的两个纳什均衡产量之间，企业2相应作出反应，这一特征，在考虑了相同利他因子的情况下仍然成立。成本信息不完全公开下的最优期望利润，可能会比成本信息完全公开下的最优期望利润小，但是不失为化被动为主动的最优竞争策略。而两个企业总产量随着利他因子的增加而减少，这为企业在成本信息不完全公开下的反垄断提供决策参考。结论推广到n个企业成本信息不完全公开的竞争是否成立，或一般化为企业间的差异利他，结论会怎样改变，有待进一步论证。

[1]J von Neumann，Morgenstern O著，王文Ⅰ等译：博弈论㈦经济行为[M].北京：生活·读者·新知三联书店，2004.

[2]Cournot A A.：Reachers sur les principles mathematiques de latheorie richesses[M].Paris：Edward Elgar Publishing，1838.

[3]Nash J F.：Non-coope rative Games[J].Annals of Matimatics，1951（2）.

[4]Watson.J著，费方Ⅱ等译：策略博弈论导论[M].上海：格致出版社，2010.

[5]Harsanyi J C.：Games with incomplete information played by players[J].Management Science，1967—1968（14）.

[6]俞建：博弈论选讲[M].北京：科学出版，2014.

[7]张维迎：博弈论㈦信息经济学[M].上海：格致出版社，上海人民出版社，2012.

[8]李传志、杨光：不完全信息的古诺模型分析[J].山西财经大学学报，2007，29（2）.

[9]夏少刚、张大乐：不完全信息下贝叶斯纳什均衡的转化[J].东北财经大学学报，2006（4）.

[10]Marco G，Morgan J.：Slightly altruistic equilibria[J].J Optim Theory Appl，2008，137（2）．

[11]王能发：基于轻微利他均衡的古诺博弈研究[J].重庆师范大学学报（自然科学版），2014，31（4）.

（责任编辑：张琼芳）

2014年度贵州财经大学教学质量㈦教学改革项目。