结合经验模态分解和Gabor滤波的高光谱图像分类
2016-04-25王立国宛宇美路婷婷杨月霜
王立国, 宛宇美, 路婷婷, 杨月霜
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
结合经验模态分解和Gabor滤波的高光谱图像分类
王立国, 宛宇美, 路婷婷, 杨月霜
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
摘要:针对传统实施于原始数据空间的纹理提取方法的不足,采用经验模态分解理论提取高光谱图像中空间结构明显的固有模态分量,并在提取出的分量上进行Gabor滤波操作,将传统纹理提取方式转移到变换域上进行,提出了一种基于二维经验模态分解融合空间信息的高精度纹理提取算法。对两个数据集进行仿真实验,实验结果表明改进算法有效地提高了高光谱图像分类精度且抗噪性能良好,提出算法性能明显优于传统Gabor-PCA算法,能够更大程度挖掘高光谱图像空间信息。
关键词:高光谱图像;图像分类;空间信息;经验模态分解;Gabor滤波
高光谱和空间分辨率遥感影像近几年受到越来越多的关注,这类高光谱数据被广泛应用于城市地区土地覆盖/土地利用制图上。为了广泛利用高光谱图像的空间结构以及光谱信息,国内外学者已展开了若干研究。其中Fauvel将光谱信息与提取的目标特征信息重构目标特征矢量,并通过分类实验验证了提出方法的有效性[1]。Camps-Valls在分类过程中分别构造谱域信息与空域信息的核函数,并且研究了几种核函数组合方式[2]。Tarabalka利用聚类算法分割高光谱图像,进而结合分割结果以及光谱特征分类结果,总体分类结果有一定提高[3]。
纹理分析在计算机视觉领域有着广泛的应用。研究表明,Gabor纹理信息能够很好地表示有用的空间信息,在纹理分割研究中展现了良好的应用价值[4]。文献[5]将Gabor纹理信息应用于面部图像的表示和识别。文献[6]讨论了在高光谱图像分类技术中引入Gabor纹理信息。
经验模态分解(EMD)是在1998年由N.E.Huang[7]提出的一种对于非平稳、非线性信号处理效果理想的方法,它能够将信号分解成有限个固有模态函数(IMF)和一个残差信号。EMD提取信号本质特征的方式是自适应的,对比小波变换,EMD表现出了更好的时频特性,在高光谱数据特征提取上的潜力和优势是十分明显的[8]。
在变换域上进行高光谱数据分析和处理已在分类、压缩、超分辨等方面广泛使用,具有减小信息冗余、降低噪声干扰等优点,显示出良好的效果[9]。针对现有Gabor纹理提取方法对高光谱图像空间信息提取不足的问题,提出一种基于经验模态分解的Gabor纹理提取算法。
1支持向量机分类算法
支持向量机(SVM)是一种快速,高效的机器学习算法,因其较好的分类性能而广泛应用于高光谱图像分类问题[10]。SVM基本原理介绍如下。
设样本数据为xi∈Rd,yi∈{+1,-1}为相应类别的样本标号,i=1,2,…,n。一般形式的线性判别函数为g(x)=〈ω,x〉+b分类面表示为〈ω,x〉+b=0。式中x=[x1x2…xd]T是d维特征矢量,权向量表示为ω=[ω1ω2…ωd]T。b为常数,称为阈权值。
当所要解决的问题是非线性时,SVM引入非线性映射φ(·)的方法,这样,原始空间不能线性分开的数据点就转化成了高维空间上的可分点。此时通过解决式(1)来获得最优分类超平面:
(1)
式中:ξi为松弛项,常值C>0,它代表对分类结果不正确样本的惩罚程度。约束条件为
(2)
为了求解问题(1),建立并求解其对偶问题,即最大化下式函数:
(3)

(4)
SVM是二元分类器,将其扩展到多类别问题通常是组合多个二值分类器。1-a-r(1-against-rest)多类分类器和1-a-1(1-against-1)多类分类器是2种常用的多类分类器结构。实验采用1-a-r型支持向量机来进行高光谱数据分类。
2空谱结合分类
2.1经验模态分解
经验模态分解(empiricalmodedecomposition,EMD)法是一种新型自适应信号时频处理方法[12],它能够将复杂数据表示成数量有限并且较少的固有模态函数(intrinsicmodefunction,IMF)分量的加和形式。固有模态函数满足如下条件[8]:
1) 函数的局部极值点和过零点数在整个时间范围内必须相等,或最多相差为一;
2) 在任意时刻,由局部最大值确定的上包络和由局部最小值确定的下包络的平均必须为零。
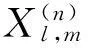
1) 找到当前波段上全部局部极大值点和局部极小值点;
2) 使用插值算法把局部极大值拟合成上包络面Emax(i,j),局部极小值拟合成下包络面Emin(i,j);
(5)
(6)
5) 检查结果是否符合迭代结束条件SD<τ,SD表示为
(7)

6) 当得到IMF函数后,更新残余量Rm(i,j)为
(8)
如果此残余量不含极值,此EMD程序终止。如果残余量含极值,将此残余量Rm(i,j)作为初始输入从步骤1)继续求解。
综上所述,光谱原始波段图像Xl(i,j)被所求得的IMF函数及残余量重构,表达式为
(9)
2.2Gabor纹理特征提取
Gabor函数形成的二维Gabor滤波器具有在空间域和频率域同时取得最优局部化的特性。因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性的局部结构信息[13]。在空域,一个二维的Gabor滤波器是一个正弦平面波调制的高斯核函数,一般表达式为
(10)
式中:图像中某点像素位置参数x和y,x′=xcosθ+ysinθ,y′=-xsinθ+ycosθ,f和θ各自表示Gabor函数的频率和方向,φ为Gabor函数相角,γ为空间宽高比,Gabor函数高斯因子的标准差是σ,σ的大小根据正实数带宽b(一般是1)改变。它们之间的关系为
(11)
式中:λ=1/f。
由于图像中各种纹理包含各自的带宽和中心频率,单独的Gabor滤波器并不能提取全部的纹理信息,因而对纹理图像滤波时,需要采用一系列包含不同带宽和频率的Gabor滤波器。实验中设置了5个尺度6个方向的滤波器组:

(12)
所得Gabor特征集通过输入图像与这30个滤波器组卷积而得到
(13)
2.3变换域的纹理特征提取及空谱信息融合分类
不同于原始Gabor纹理提取方法从原始高光谱图像中直接提取纹理信息的方式,提出一种结合二维经验模态分解的变换域纹理提取方法,并通过分类实验验证提出方法的有效性,实验流程图如图1所示。
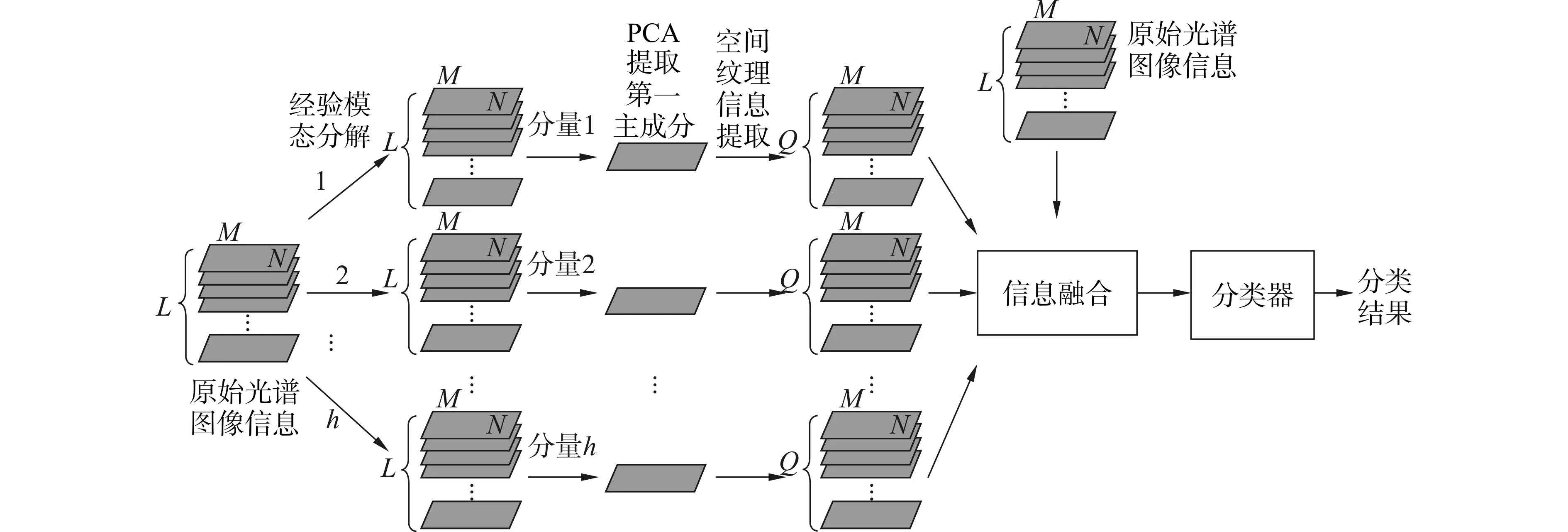
图1 纹理提取算法步骤Fig.1 Steps for texture extraction algorithm
图1中,以L波段高光谱图像为例,每一波段包含M×N个像素点;分量1、分量2、分量h分别表示第h个EMD变换域分量;Q表示Gabor滤波器组数。
首先,求输入信号X′的局部极值,利用插值算法求出上包络、下包络和均值包络。然后将输入信号减去均值包络,获得第一个分量D1(i,j),判断D1(i,j)是否满足终止迭代条件。如果满足则D1(i,j)是第1个IMF,如果不满足则把D1(i,j)作为初始信号开始重新迭代,直到满足终止条件,此时获得第1个IMF,并求得残余量R1(i,j)。判断残余量是否包含极值,如果此残余量不含极值,EMD程序终止。假如残余量含极值,以此残余量R1(i,j)当做初始信号继续求解下一个IMF和下一个残余量,当残余量不含极值,获得全部IMF,EMD程序终止。
由于固有模态函数的本质是信号在不同频率范围内原信号的本质特征,原信号噪声的集合表示为残差形式,所以提取信号的本质特征可通过保留IMF分量和丢弃残余量来实现。在改进纹理提取算法中,经验模态分解只保留低阶的IMF分量,高阶的IMF分量及残余量不予考虑。这样,就可以保证包含空间关系信息的低阶IMF分量被保留,而较高阶的IMF分量(通常缺乏空间结构信息)将被丢弃。
其次,经验模态分解之后,原始高光谱图像被表示为有限个IMF分量的集合,对各IMF集合利用主成分分析法(PCA)提取各集合数据的第1主成分。
最后,进行空间纹理滤波处理。空间纹理滤波建立在各主成分分析提取的第1主成分上。
针对改进的纹理提取算法,采用两种信息融合方式,并通过SVM分类算法验证结果的有效性。
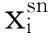
(14)
方法2:图像层融合,实验中采用原始高光谱图像经PCA提取前三维,与纹理数据进行重组,利用所得重组数据进行分类。
3分类实验及结果评价
3.1实验数据
实验选用2组常用来验证高光谱图像分类算法的高光谱数据,分别为印第安针叶林、帕维亚大学数据。
第1数据集为1992年6月由AVIRIS拍摄的印第安纳西北部农业区高光谱航空影像,像素信息144×144,200维波段。该数据光谱范围0.4~2.5 μm,空间分辨率20 m。在原始的16类样本数据中忽略小样本集数据,采用样本数量最多的9类地物进行分类研究。这9类样本类别及样本数量如表1所示。

表1 实验所用印第安针叶林数据
第2数据集是包含340×610像素和103维波段数据。该数据光谱范围是0.4~0.85 μm,空间分辨率为1.5 m。本实验选取数据包含8类地物的样本数据来验证文中所提方法的有效性,这8类样本及数量如表2所示。

表2 实验所用帕维亚大学数据
3.2参数设置
实验结果通过不同的训练样本数据率(training data rates,TDR)来进行证明。TDR为5%表示随机抽取每类样本数据的5%为训练样本,剩余样本做测试样本。二维经验模态分解部分,对于每一波段图像,以尺度100将图像镜像延拓;插值方式采用cubic三次多项式插值;τ取0.3。SVM采用高斯径向基核函数,并采用网格搜索法搜索最佳参数(数据集1中惩罚系数为1 000,高斯径向基核函数参数σ=1.8,数据集2中分别为700和1.2)。
3.3 结果与讨论
按照前文算法流程对高光谱图像进行分类实验,实验结果如图2所示。
图2(a)为原始高光谱图像;图2(b)为利用SVM对原始高光谱数据9类地物分类结果;图2(c)为对原始高光谱图像PCA降维后取第一主成分分量利用Gabor滤波器组提取纹理信息,与原始高光谱图像特征层融合经SVM分类结果;图2(d)为改进方法。从图2可以看出,改进方法进一步消除了“麻点”现象。


图2 印第安针叶林TDR为5%时的分类效果Fig.2 Classification results of Indian coniferous forest with TDR of 5%
图3为印第安针叶林9类地物各类别精度对比,可以看出,改进方法对各类地物分类精度较Gabor-PCA方法有不同程度的提高。

图3 印第安针叶林9类地物OA柱状图Fig.3 Histogram of OA on Indian coniferous forest datasets
利用整体精度(OA)和Kappa系数对实验结果进行表征,以此评价各方法的实验结果,各种方案分类评价结果如表3所示。

表3 各种方案分类评价
由表3分析得出,对于只应用SVM分类的结果来说,结合空间信息后分类精度已经有很大程度的提高。然而,由于原始高光谱图像存在噪声干扰、信息冗余等因素,直接对原始图像提取纹理信息并不能达到高精度分类的目的。改进方法在对原始图像经过自适应的二维经验模态分解之后,对于分解所得IMF分量分别提取纹理信息,去除掉部分冗余信息的同时也增加了可融合的纹理信息。在TDR为5%的情况下可使整体精度从91.05%提高到94.79%。总体分类精度得到明显提高。
表4 印第安针叶林不同IMF分量数对分类结果的影响
Table 4Effect of different IMF number on Indian coniferous forest datasets
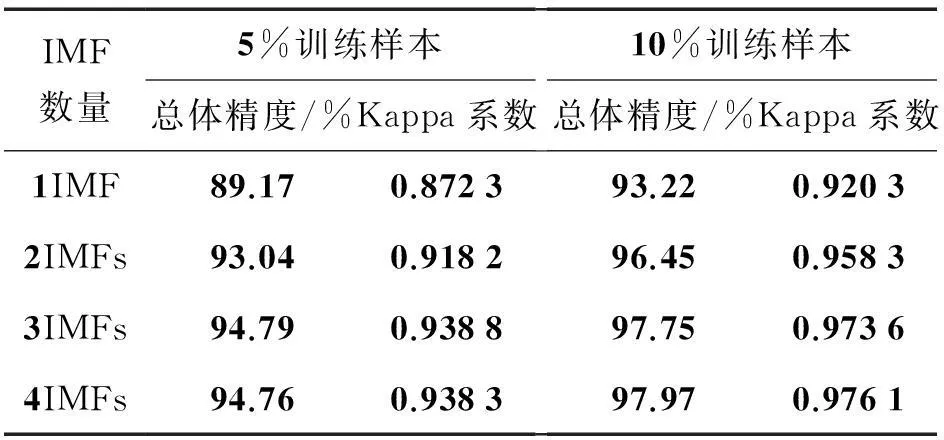
IMF数量5%训练样本总体精度/%Kappa系数10%训练样本总体精度/%Kappa系数1IMF89.170.872393.220.92032IMFs93.040.918296.450.95833IMFs94.790.938897.750.97364IMFs94.760.938397.970.9761
此外,从表4可以看出,随着融合信息的增加,精度的提高已经不是很明显了。特别的,在训练样本数量为总体5%时,融合前4个IMF对比融合前3个IMF的精度反而有下降。这是纹理信息冗余所导致的,因此,综合计算量及分类精度的折中考虑,只利用前3个IMF即可获得较好效果。
为了证明改进方法的有效性,利用帕维亚大学数据进行验证。此实验的信息融合方式采用图像层融合,TDR为5%,分类结果如图4所示。
精度评价结果如表5所示。由表5可得改进方法对于图像层融合方式同样有效。
表6给出针对帕维亚大学数据不同IMF分量数对分类结果的影响,可以看出在保留3个IMF分量时结果最优。
此外,为了验证改进方法对含噪声高光谱图像分类处理的有效性,对两数据集所有波段添加方差为σ2的白噪声,并利用所得噪声数据进行分类实验。数据集1中TDR为5%,数据集2中TDR为2.5%,采用整体精度OA和Kappa系数表征分类效果,精度评价结果如表7、8所示。


图4 帕维亚大学数据TDR为5%时的分类效果Fig.4 Classification results of Pavia university datasets with TDR of 5%
Table 5Evaluation of classification methods of Pavia university datasets with TDR of 5%

指标SVMGabor-PCA改进算法总体精度/%91.7297.2298.01Kappa系数0.87450.95800.9701
表6帕维亚大学不同IMF分量数对分类结果的影响
Table 6Effect of different IMF number on Pavia university datasets

IMF数量5%训练样本总体精度/%Kappa系数1IMF97.430.96132IMFs97.630.96443IMFs98.010.97014IMFs97.960.9692
将噪声数据分类精度评价结果以折线图方式表示,如图5、图6所示。从图中可以看到,噪声的加入对普通SVM分类结果的影响是很大的,当噪声方差在20~120变化时,两数据集SVM分类精度损失分别超过2%和1%。随着噪声的增大,此时的含噪图像在SVM分类方法下终将因为分类精度的降低而失去研究意义。而原始Gabor-PCA方法可以缓解噪声带来的影响,原因是PCA方法本身包含去除噪声和冗余的特点,经过空间信息融合之后分类精度有很大提高。改进方法也具有良好的抗噪声性能,经验模态分解根据信号本身的特点滤去包含噪声的高频IMF分量及残余量,这对接下来的处理提供了消噪数据。同时,IMF分量的有限性也保证了最大程度融合纹理信息的同时又不至于纹理信息融合过度。当噪声方差在20~120变化时,整体分类精度并没有随着噪声强度的增加而有明显的下降。在含噪图像测试下,改进方法对分类性能的提升仍优于原有Gabor-PCA方法,再次证明了该方法的有效性。

表7 印第安针叶林噪声数据对分类结果的影响
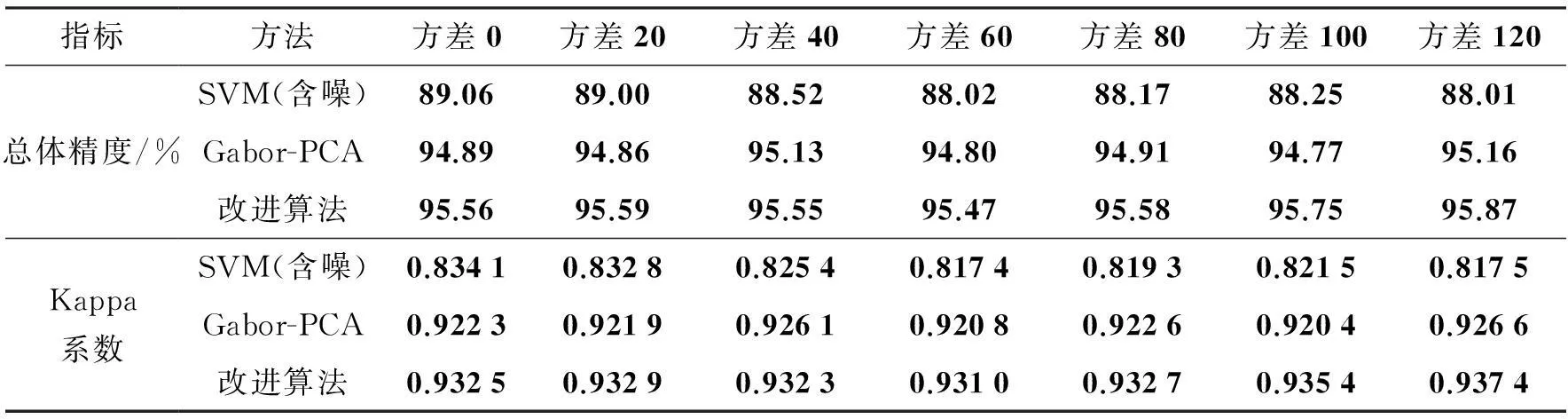
表8 帕维亚大学噪声数据对分类结果的影响

图5 印第安针叶林不同方差噪声数据对分类结果的影响Fig.5 Effect of noisy data with different variance on Indian coniferous forest datasets

图6 帕维亚大学不同方差噪声数据对分类结果的影响Fig.6 Effect of noisy data with different variance on Pavia university datasets
4结论
1)与传统的Gabor-PCA算法相比,该算法在精度上明显提高很多,而且在抗噪性能上也有优秀的表现。
2)与传统高光谱Gabor纹理提取方法研究思路不同,提出算法将滤波操作转移到变换域上进行,最大程度保留原始数据信息的同时更加高效地挖掘了空间信息,为高光谱图像的纹理提取开辟了新的思路。
3)经实验验证,该算法很大程度消除了分类问题中样本错分现象,而且精度很高,不受噪声影响,是一种优势明显的算法策略。
参考文献:
[1]FAUVEL M, BENEDIKTSSON J A, CHANUSSOT J, et al. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles[J]. IEEE transactions on geoscience and remote sensing, 2008, 46(11): 3804-3814.
[2]CAMPS-VALLS G, GOMEZ-CHOVA L, MUNOZ-MARI J, et al. Composite kernels for hyperspectral image classification[J]. Geoscience and remote sensing letters, 2006, 3(1): 93-97.
[3]TARABALKA Y, BENEDIKTSSON J A, CHANUSSOT J. Spectral-Spatial classification of hyperspectral imagery based on partitional clustering techniques[J]. IEEE transactions on geoscience and remote sensing, 2009, 47(8): 2973-2987.
[4]LI Chaorong, DUAN Guiduo, ZHONG Fujin. Rotation invariant texture retrieval considering the scale dependence of Gabor wavelet[J]. IEEE transactions on image processing, 2015, 24(8): 2344-2354.
[5]王科俊, 邹国锋. 基于子模式的Gabor特征融合的单样本人脸识别[J]. 模式识别与人工智能, 2013, 26(1): 50-56.
WANG Kejun, ZOU Guofeng. A sub-pattern Gabor features fusion method for single sample face recognition[J]. Pattern recognition and artificial intelligence, 2013, 26(1): 50-56.
[6]JIA Sen, SHEN Linlin, DENG Lin. Band selection-based Gabor wavelet feature extraction for hyperspectral imagery classification[C]//Proceedings of the 4th workshop on hyperspectral image and signal processing. Shanghai, China, 2012: 1-4.
[7]HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. London, 1998, 454: 903-995.
[8]沈毅, 张敏, 张淼. 基于互信息波段选择和经验模态分解的高精度高光谱数据分类[J]. 激光与光电子学进展, 2011, 48(9): 59-66.
SHEN Yi, ZHANG Min, ZHANG Miao. Mutual information bands selection and empirical mode decomposition based support vector machines for hyperspectral data high-accuracy classification[J]. Laser and optoelectronics progress, 2011, 48(9): 59-66.
[9]王立国, 赵妍. 基于MAP的高光谱图像超分辨率方法[J]. 光谱学与光谱分析, 2010, 30(4): 1044-1048.
WANG Liguo, ZHAO Yan. MAP based super-resolution method for hyperspectral imagery[J]. Spectroscopy and spectral analysis, 2010, 30(4): 1044-1048.
[10]KUO B C, HO H H, LI C H, et al. A kernel-based feature selection method for SVM with RBF kernel for hyperspectral image classification[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2014, 7(1): 317-326.
[11]张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32-42.
ZHANG Xuegong. Introduction to statistical learning theory and support vector machines[J]. Acta automatica sinica, 2000, 26(1): 32-42.
[12]DEMIR B, ERTURK S. Empirical mode decomposition of hyperspectral images for support vector machine classification[J]. IEEE transactions on geoscience and remote sensing, 2010, 48(11): 4071-4084.
[13]肖倩. 结合空间信息与光谱信息的高光谱图像分类研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 35-38.
XIAO Qian. Combination of spatial information and spectral information for hyperspectral imagery classification[D]. Harbin: Harbin Engineering University, 2013: 35-38.
Hyperspectral image classification by combining empirical mode decomposition with Gabor filtering
WANG Liguo,WAN Yumei,LU Tingting,YANG Yueshuang
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract:Considering the shortcomings of traditional texture extraction methods implemented in original data space, in this paper we use the empirical mode decomposition theory to extract the intrinsic mode components of a distinct spatial structure from a hyperspectral image, and perform Gabor filtering on these extracted components. We transferred the traditional texture extraction method to the transform domain. In this way, we propose using a high-precision texture extraction algorithm for decomposing and integrating spatial information based on two-dimensional empirical mode decomposition. We carried out simulation tests on two datasets, and the results show that the improved algorithm effectively improves the classification accuracy of hyperspectral images and has good noise suppression performance. The proposed algorithm is thus clearly superior to the traditional Gabor-PCA algorithm, and can mine hyperspectral image spatial information to a greater extent.
Keywords:hyperspectral image; image classification; spatial information; empirical mode decomposition; Gabor filter
中图分类号:TP751
文献标志码:A
文章编号:1006-7043(2016)02-0284-07
doi:10.11990/jheu.201411032
作者简介:王立国(1974-), 男, 教授, 博士生导师.通信作者:王立国, E-mail: wangliguo@hrbeu.edu.cn.
基金项目:国家自然科学基金资助项目(61275010); 国家教育部博士点基金资助项目(20132304110007); 黑龙江省自然科学基金资助项目(F201409); 中央高校基本科研业务费资助项目(HEUCFD1410).
收稿日期:2014-11-10.网络出版日期:2015-12-15.
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20151215.1141.022.html
