双断点塑壳断路器触头固有分断时间等计算分析与优化设计

周光照

（温州大学机电工程学院，浙江温州，325035）



双断点塑壳断路器触头固有分断时间等计算分析与优化设计

周光照

（温州大学机电工程学院，浙江温州，325035）

摘要：通过对双断点塑壳断路器触头机构的动作过程的受力与运动的详尽分析，应用SolidWorks软件创建了符合实际情况的物理模型与动力学模型，然后应用MATLAB软件，以双断点断路器触头机构相关参数如杠杆弹簧刚度、下连杆长度、动触头质量等多种参数的变化为实例进行优化设计，计算出对应的触头分断速度、固有分断时间、超行程等断路器关键技术数据，同时得到相应情况下的触点P的运动曲线图，为双断点断路器触头机构的优化设计或逆向工程提供依据和参考。

关键词：双断点；触头机构；分断时间

引言

塑壳断路器是低压断路器的一种，由于其结构紧凑、体积小、安装方便等原因而得到广泛应用。断路器触头机构直接影响断路器的分断性能，是断路器的关键部件。塑壳断路器根据触头的数量，可分为单断点与双断点塑壳断路器，而双断点塑壳断路器根据触头运动方式不同又可分为直动式和转动式。由于双断点塑壳断路器可以形成双电弧区，灭弧能力更强，因此相比于单断点断路器性能更好[1]。但由于旋转式双断点塑壳断路器（以下简称双断点断路器）相对单断点塑壳断路器内部结构更紧凑而复杂，所以设计起来也更加困难，其研究价值与应用前景也相对更大。

国内外针对单断点塑壳断路器（以下简称单断点断路器）触头分断机构的优化设计研究已取得不少成果：文献[2]首次提出了单断点断路器触头分断机构的分断动作过程是四连杆转化五连杆的运动，并对其做了全面的动力学分析，进而提出了一种定量计算触头分断速度的方法；陈德桂等人则采用ADAMS软件对其进行优化设计[3～4]；还有学者对虚拟样机软件进行二次开发，以便提高设计效率[5～6]。但针对双断点塑壳断路器（以下简称双断点断路器）的研究则相对较少，其中：文献[7]针对双断点触头分断结构进行了动态仿真以及优化，而其文中所依据的模型中的上下连杆轴的位置和分断时其死区的定位，尤其是触头分断速度的确定方法等，与文献[3～6]及其他文献一样都存在不少误解，这必然造成输入仿真软件进行分析和优化设计研究所形成的计算模型错误，故难以进行有效应用；其他文献则集中在对双断点断路器结构优缺点的分析[8]以及电动力对触头压力的影响方面问题的研究[9]，而对真正影响旋转式双断点断路器分断性能和使用寿命的固有分断时间和触头终压力等的分析与计算未见提及。本文将通过对双断点断路器的结构和受力特征分析，采用MATLAB软件进行定量计算双断点断路器固有分断时间等特性参数的方法，并以杠杆弹簧和触头弹簧刚度、下连杆长度、动触头质量等要素为设计变量，固有分断时间、触头终压力等为目标函数进行优化设计，从而为缩短双断点断路器的固有分断时间，即提高断路器分断能力提供有效的依据。

1　双断点断路器触头机构运动过程分析

断路器触头机构的动作分为合闸、分闸、分断、再扣四种。

双断点断路器（合闸状态）触头机构实物和简化模型如图1所示，其中，BC为上连杆、CE为下连杆。合闸动作是在跳扣固定不动，逆时针搬动手柄，杠杆弹簧力驱使转轴逆时针转动，轴C进入死区，实现动、静触头接触并压紧，最终位置是轴C在弹簧力与触头反力等作用下紧压在跳扣上，整个系统平衡即触头机构处于合闸状态，即图1所示状态。

图1　触头机构实物和简化模型

分闸动作是跳扣固定，顺时针搬动手柄，当杠杆弹簧越过BC连线，杠杆弹簧力及触头反力等驱使转轴顺时针转动，实现动、静触头分离，触头分断机构最终位置为分闸状态。

分断动作最为复杂：跳扣失去约束，杠杆弹簧力及触头反力等驱使跳扣和转轴逆时针快速转动。分断动作初时，轴C依然被压紧在跳扣上即上连杆与跳扣相对静止，故此时触头机构是由OE、CE、OD、CD组成的四连杆机构；动、静触头分离后，触头反力消失，当触头机构继续运动到一定位置时，B点与跳扣分离，于是系统变成由OE、CE、BC、BD、OD组成的五连杆机构，由于此时系统具有2个自由度，与手柄位置无关（故为方便分析起见，后文以带电操或手操的双断点断路器即杠杠位置不变的情况为例进行分析），且触头机构最终位置为自由脱扣状态，可见触头机构分断动作是一个四连杆变五连杆的过程。

再扣动作则是顺时针推动手柄使锁扣重新锁定，触头机构由自由脱扣状态恢复为分闸状态的过程。

2　双断点触头机构各杆件运动关系及受力分析

2.1双断点断路器触头机构的受力分析

如上所述，触头机构的分断过程是一个四连杆变五连杆的过程，并且在四连杆运动过程中，存在着动、静触头未断开与断开两种情况，因此应分别进行分析与计算。

分断动作初始阶段，轴C因杠杆弹簧力F作用被压紧在跳扣上，此时上连杆BC与跳扣无相对运动，故两者可视为杆CD，如图2所示（为简明起见，各轴的摩擦力偶未画出）。

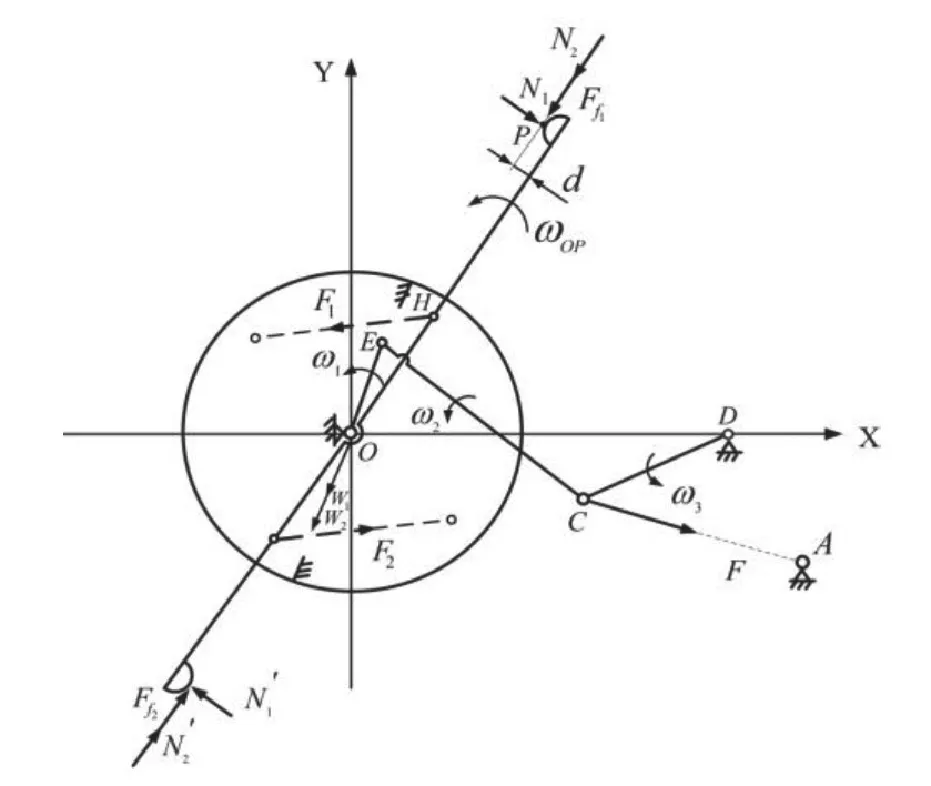
图2　动、静触头未分离状态下触头机构分断过程的运动与受力简图

由图2可知，由于此时动、静触头未完全分离，与单断点触头受力不同，此时的双断点动触头两端同时受到大小相等、方向相反的触头反力（包括摩擦力）作用，此时，触头杆受触头反力的作用，使其与转轴处于分离状态。由分析可知，触头弹簧两端分别与触头杆和转轴相连，故触头杆和转轴所受的触头弹簧拉力为内力，不必考虑。另外，由于转动式双断点两端分别受到垂直于触头杆的两个大小相等、方向相反的触头反力N1、N2作用和平行于触头杆方向上的分力N1′、N2′与摩擦力Ff1、Ff2的作用，因此，动触头所受力对O点的力矩和各轴摩擦力偶可归化为一个正力偶M1及两个阻力偶M2、M3。此外，虽然转轴与触头杆的质量相对与其他杆件较大，但因其结构对称，两者合力通过O点，故其对O点的矩为零。因此，整个触头机构的分断运动是在杠杆弹簧力和触头反力等及相关摩擦力作用下进行的。

通过进一步分析可知：触头机构在触头反力和杠杠弹簧力等力作用下继续运动到动、静触头分离瞬间，触头杆与转轴由分离状态变为压紧状态，即触头杆由原来受触头反力和触头弹簧力作用变至触头杆与转轴的接触压力，而在此过程中，触头反力由最大值逐渐变至零。当动、静触头完全分离瞬时开始，在触头弹簧力的作用下触头杆也随之完全压紧在转轴上，由于触头弹簧两端分别与触头杆和转轴相连，故触头杆所受的触头弹簧拉力和触头杆所受的转轴反力均为内力，整个触头机构只在杠杆弹簧力及相关摩擦力等作用下运动，如图3所示。

图3　分断过程中动、静触头分离状态下触头机构为四连杆时的运动与受力简图

当触头机构在杠杠弹簧力的作用下继续运动，直至触头机构由四连杆机构变为五连杆机构并继续运动，最终完成断路器的分断过程[10]，其运动与受力如图4所示。

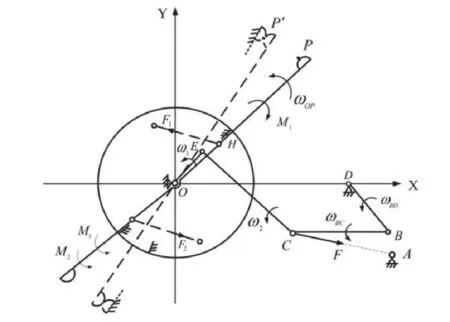
图4　分断过程中动、静触头分离状态下触头机构为五连杆机构时的运动与受力简图

由上文分析可知，E点虽不在触头杆上，但两者的角速度、角位移等具有一定的关联关系，只要通过机构的组成特点，便能计算出动触头及其他各部件的运动和力学等参量。因触头杆的动作是通过转轴来带动，故当触头连杆未接触转轴上之前，其一直保持与静触头接触即处于静止状态。综上分析，触头机构的受力与运动简图如图5所示。

2.2双断点断路器触头机构各杆件角位移关系求解

在图5中，令L1、L2、L3、L4分别为杆OE、CE、CD、OD的长度，根据复数矢量法可得矢量方程：

即：

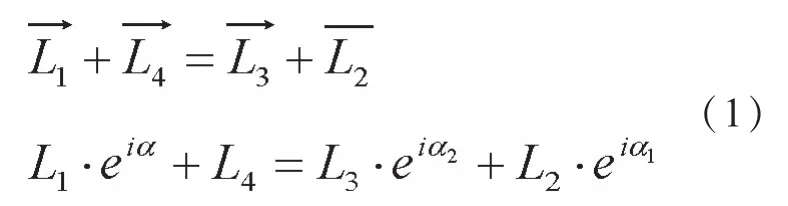
按欧拉公式展开得：

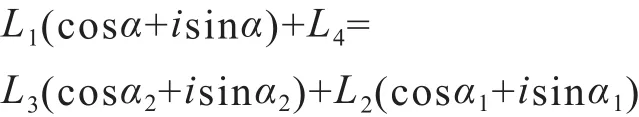
令虚实部分别相等，最终可解得：

其中：

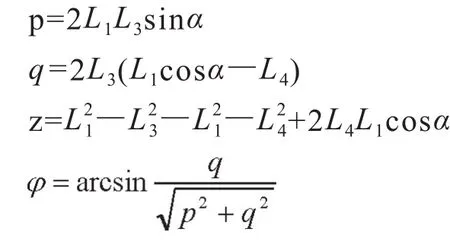
2.3双断点断路器触头机构相关杆件角速度关系求解

令ω1、ω2、ω3分别为杆OE、CE、CD的角速度，将式（1）对时间t求导得：

按欧拉公式展开，实、虚部分别相等得：

同理可得：

2.4双断点断路器触头机构相关杆件角加速度关系求解

令a2、a3分别为杆CE、CD的角加速度，将式（2）对时间求导得：

消去a3，并按欧拉公式展开，最终可得：

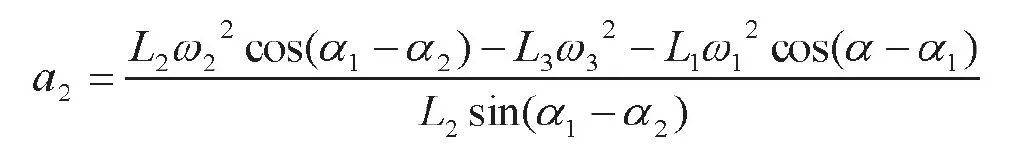
同理可得：

2.5双断点断路器触头机构等效力矩的求解

2.5.1触头反力及其摩擦力对O点的力矩

由图5可知，触头反力及其摩擦力对O点的力偶矩为：

2.5.2杠杠弹簧BA对O点的力矩

令l0为杠杠弹簧CA的自由长度，ln为BA任意时刻的长度，则：

F=K(ln－l0)

将F分解为沿CE、CD方向的两个力FCE、FCD，则杠杠弹簧力F对O点的力矩为：

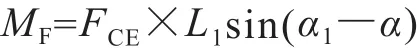
2.5.3触头机构等效力矩

触头机构的等效力矩等于触头机构中各杆上作用的力矩和力偶距的代数和：

式中M4为各铰链轴销处所受到的摩擦力偶距。

2.6双断点断路器触头机构等效转动惯量的求解

令V1、V2、V3分别为杆OE、CE、CD质心的速度，m1、m2、m3为各杆质量，J1、J2、J3为杆OE、CE、CD对其质心的转动惯量。等效杆为OE，等效转动惯量为Jv，则有：

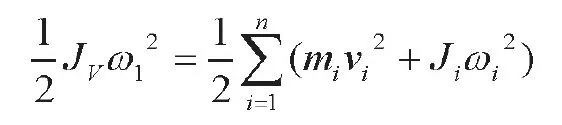
即：

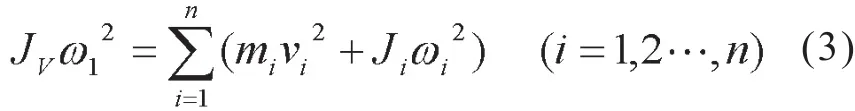
令l1、l2和l3分别为杆OE、CE和跳扣的质心到其转动中心的距离，则根据触头机构的几何结构和动力学关系，由式（3）可以得到：

其中：

2.7触头杆角速度及动触头接触点处分断速度求解

由以上分析知：等效力矩Mv，等效转动惯量Jv均为α的函数，因此可得：

从而求得杆OE即转轴的角速度 ：

其中：α0为杆OE的初始角位移。

由上文分析知：当触头杆与转轴上H点接触时，触头杆才开始运动，此时转轴转过的角度为β，则所需的时间即为双断点断路器的固有分断时间：

由于在t1时间内，触头杆一直保持静止状态，故触头杆的角速度ωOP可表示为：

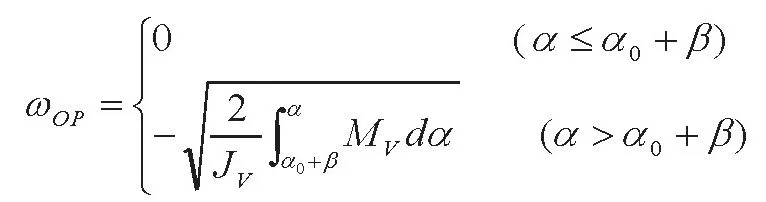
其中：α0+β为触头杆的初始角位移。

则触头杆点P处的运动速度vOP为：

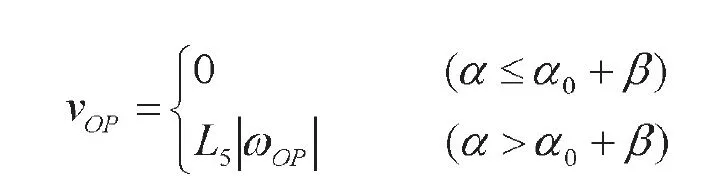
3　双断点断路器触头机构的优化设计

下文以某型100A双断点断路器为例，利用MATLAB软件对该断路器部分构件参数进行优化设计计算与分析，其主要结构件的有关参数为：L1=5 mm、L2=20mm、L3=20mm、L4=30mm、L5=20mm、m1=20g、m2=5g、m3=10g、杠杠弹簧刚度系数40N/mm、触头弹簧刚度系数7N/mm。

3.1杠杆弹簧的刚度对分断速度等的影响

杠杆弹簧是触头机构动作的主要驱动力，采用不同的杠杆弹簧刚度系数，动静触头分离瞬间的触头运动速度（简称分断速度）及固有分断时间等参数的计算结果如表1所示，触头接触点P的运动速度曲线如图6所示。

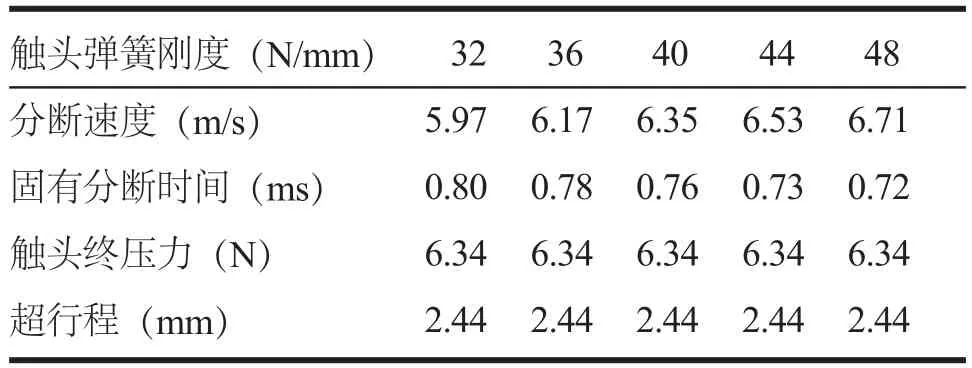
表1　杠杆弹簧刚度对触头分断速度的影响

图6　杠杆弹簧刚度对触点P的运动速度的影响

由表1和图6可知，增大杠杆弹簧刚度有利于提高分断速度和缩短固有分断时间，当然，增大杠杆弹簧刚度，会造成各杆件的受力增大，故要从优进行选择。

3.2触头弹簧刚度对分断速度等的影响

触头弹簧刚度大小的变化必然会影响分断速度、触头终压力等断路器主要性能，触头弹簧刚度变化对触头分断速度等的影响如表2所示，触头接触点P的运动速度曲线如图7所示。

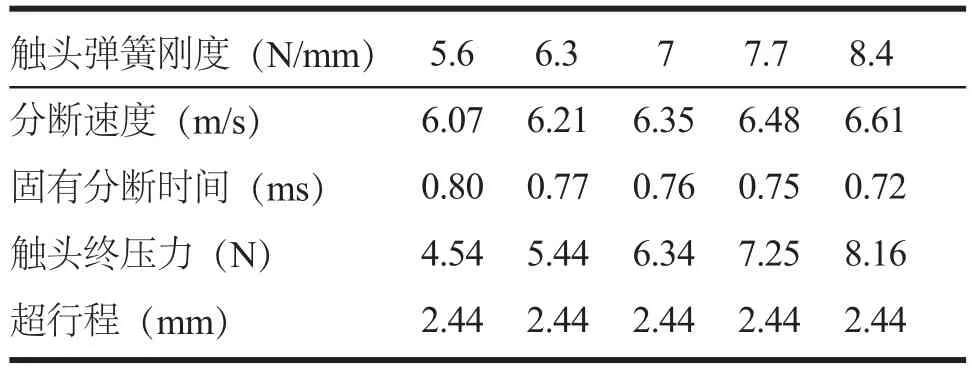
表2　触头弹簧刚度对触头分断速度的影响

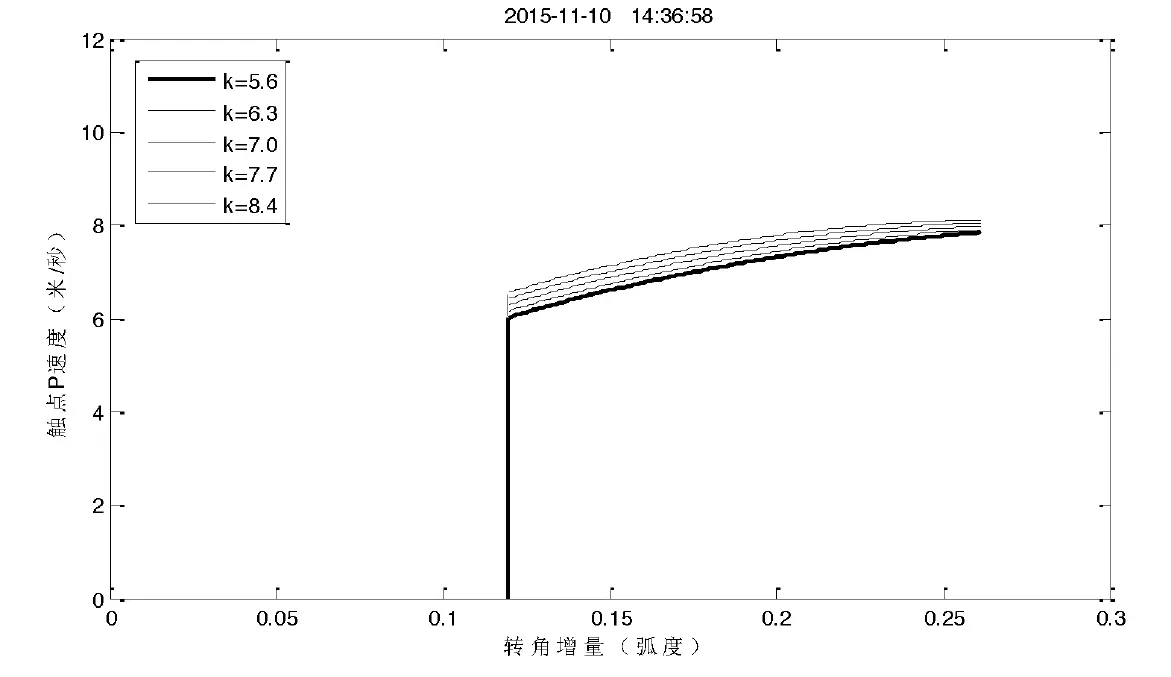
图7　触头弹簧刚度对触点P运动速度的影响

分析表2和图7可知，增大触头弹簧刚度有利于提高分断速度和缩短固有分断时间，但效果不很明显。当然，增大触头终压力，对降低触头温升有利，但合闸时动静触头的冲击力较大；反之如减小触头终压力，虽然合闸时动静触头的冲击力降低，但对降低触头温升不利。

3.3动触头质量对分断速度等的影响

显然，通过改变触头机构构件的形状和材料即改变构件的质量也可达到优化设计的目的，下面以改变动触头的质量为例，其大小变化对分断速度等的影响如表3所示，触头接触点P的运动速度曲线如图8所示。

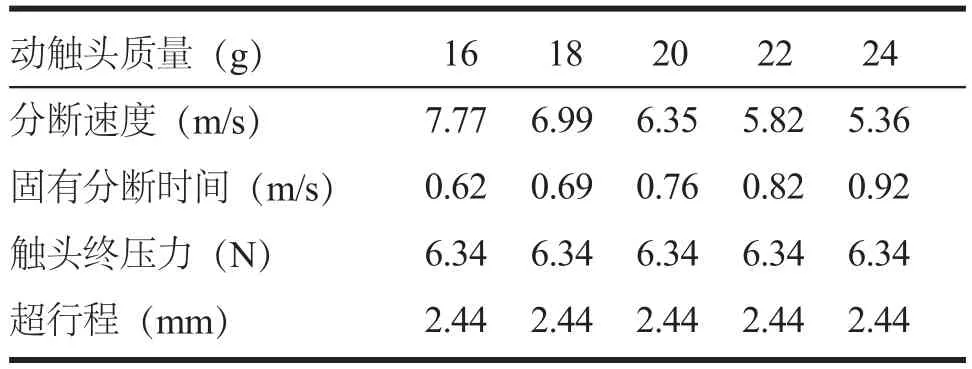
表3　动触头质量对触头分断速度的影响

图8　动触头质量对触点P运动速度的影响

由表3和图8可知，动触头质量越小分断速度越大，且影响明显，但动触头质量减小会带来强度不足的问题，从而降低断路器工作可靠性，故可通过限定其强度可变范围进行优化设计。

3.4跳扣质量对分断速度等的影响

改变跳扣的质量大小对分断速度等的影响如表4所示，点P的运动速度曲线如图9所示。

表4　跳扣质量对触头分断速度的影响

由表4和图9可知，跳扣质量变化对分断速度影响不明显，故优化设计可变范围较大。

3.5下连杆长度对分断速度等的影响

图9　跳扣质量对触点P运动速度的影响

改变下连杆长度对分断速度等的影响如表5所示，点P的运动速度曲线如图10所示。

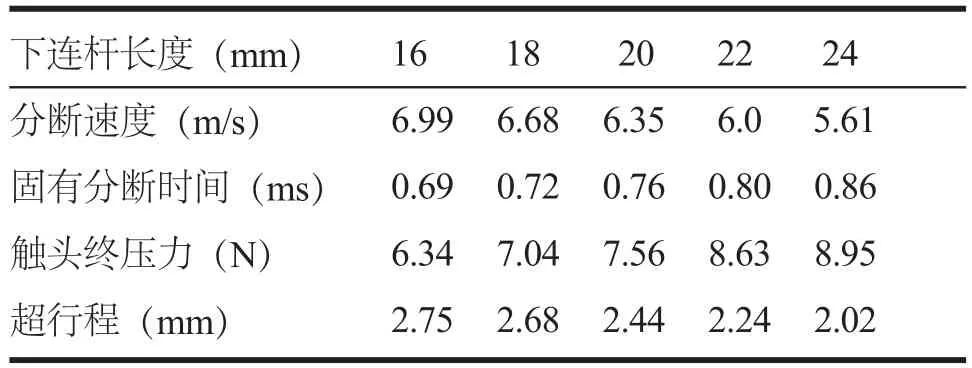
表5　下连杆长度对触头分断速度等的影响

图10　下连杆长度对触点P运动速度的影响

由表5和图10可知，下连杆长度变化对分断速度、固有分断时间、超行程、触头终压力都会带来较明显的影响，故优化设计时要注意建立合适的目标函数进行限制其变化范围。

3.6OD长度对分断速度等的影响

改变OD长度对分断速度等的影响如表6所示，点P的运动速度曲线如图11所示。

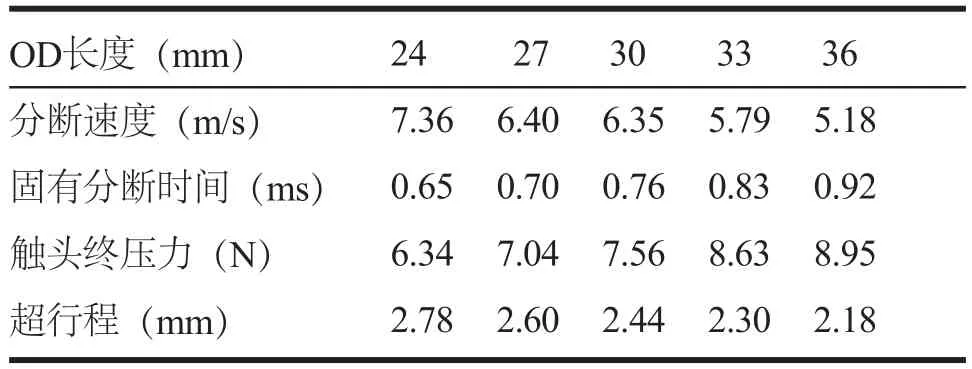
表6　OD长度对触头分断速度等的影响

图11　OD长度对触点P运动速度的影响

由表6和图11可知，OD长度变化对分断速度、固有分断时间、超行程、触头终压力都会带来影响，故优化设计时也要注意建立合适的目标函数进行限制其变化范围。

3.7同时改变杠杆弹簧与触头弹簧刚度对分断速度等的影响

同时改变杠杆弹簧和触头弹簧刚度对分断速度等的影响如表7所示，点P的运动速度曲线如图12所示。

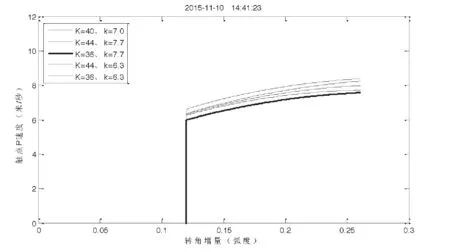
图12　杠杠弹簧、触头弹簧同时改变对触点P速度的影响

表7　杠杆弹簧与触头弹簧刚度同时改变对触头分断速度等的影响

由表7和图12可知，杠杠弹簧、触头弹簧同时改变对触头分断速度、固有分断时间会带来影响，故优化设计时应该结合两者的变化趋势建立合适的目标函数。

4　结束语

本文详细分析了触头机构的四种工作状态，利用SolidWorks建立相应的实际物理模型。同时根据双断点断路器触头机构在分断过程中受力与运动特点，建立符合实际分断工作过程的动力学模型，并对其进行全面的运动分析和受力分析，推导出计算触头机构的等效力矩、等效转动惯量以及相关杆件的角位移和角速度关系式以及定量计算双断点断路器触头机构的固有分断动作时间及各种有关特性数据的计算方法。然后应用MATLAB软件提供的各种优化算法(本文采用较常用的粒子群算法)，以双断点断路器触头机构相关参数如杠杆弹簧刚度、触头弹簧刚度、下连杆长度、动触头质量等多种参数变化为设计变量进行优化设计，根据计算结果，可直观看出各设计变量对目标函数的影响大小，从而可快速进行优化设计。此外，本文的算法简单、效果直观，并省却了采用ADAMS软件进行优化时必须对软件进行二次开发的过程，大大提高了优化设计的效率。

周光照(1990-)，硕士研究生。研究方向：产品数字化设计。

E-mail:734471388@qq.com

参考文献

[1]刘洪武,管瑞良等.双断点塑壳断路器性能特点的实验研究[J].电气开关.2009,3.

[2]叶忻泉.断路器触头分断特性的分析和计算[J].低压电器.1996,5.

[3]Liang Ji,Degui Chen.Analysis and Improvement of Linkage Transfer Position for the Operating Mechanism of MCCB[J].IEEE TRANSACTIONS ON POWER DELIVERY.2011,1.

[4]张敬菽,陈德桂等.低压断路器操作机构的动态仿真与优化设计[J].中国电机工程学报.2004,3.

[5]陈童.基于ADAMS的低压断路器操作机构仿真平台的设计研究[J].机械设计.2013.5.

[6]周宏明,沈艳等.塑壳式断路器操作机构的动力学模型及性能分析[J].计算机集成制造系统.2015,5.

[7]张波,陈德桂.旋转双断点塑壳断路器机构的动态仿真与优化[J].低压电器.2007,13.

[8]季晓明.双断点断路器结构技术特点分析[J].机电原件.2015,4.

[9]顾翔,简小刚等.双断点塑壳断路器触头接触平衡问题的研究[J].低压电器.2013,15.

[10]叶忻泉，赵荣祥等.塑壳断路器触头分断速度定量计算方法的研究[J].浙江大学学报.2006,3.

Analysis and Optimization of Inherent Breaking Time for Two-Breakers Molded Case Circuit Breakers Contacts

Guangzhao Zhou
(Wenzhou University of Mechanical and Electrical Engineering,Wenzhou,Zhejiang,325035,China)

Abstract:Through a detailed analysis of the force and motion of action about contact mechanism of the two-breakers molded case circuit breaker,creating a kinetic model in line with the actual situation using SolidWorks software,and then using MATLAB software,two-breakers circuit breaker contacts with institutions spring stiffness related parameters such as leverage,changes in the length of the lower link,the movable contact quality and other parameters to optimize the design for instance,calculate the corresponding contact breaking speed,inherent breaking time,travel and other ultra-breaker key technical data,at the same time the corresponding case of contact P of motion graph provide references for optimizing the design or reverse engineering double-break circuit breaker contacts institutions.

Key words:Two-Breakers;Contact mechanism;Breaking time

作者简介：

DOI:工业技术创新 URL:http//www.china-iti.com10.14103/j.issn.2095-8412.2016.01.018

中图分类号：TM561

文献标识码：A

文章编号：2095-8412(2016)01-644-09