海洋工程中吸力锚基础水平承载力特征

刘金龙，　陈陆望，　王吉利，　汪东林

(1.合肥学院　建筑工程系, 安徽　合肥　230601; 2.合肥工业大学　资源与环境工程学院, 安徽　合肥　230009;

3.中国科学院　武汉岩土力学研究所, 湖北　武汉　430071;

4.安徽建筑大学　土木工程学院, 安徽　合肥　230601)



海洋工程中吸力锚基础水平承载力特征

刘金龙1，陈陆望2，王吉利3，汪东林4

(1.合肥学院建筑工程系, 安徽合肥230601; 2.合肥工业大学资源与环境工程学院, 安徽合肥230009;

3.中国科学院武汉岩土力学研究所, 湖北武汉430071;

4.安徽建筑大学土木工程学院, 安徽合肥230601)

摘要：吸力锚可作为深海系泊系统基础，其水平承载力与系泊点位置有关。基于三维有限元方法，考察了吸力锚基础的水平承载特性，计算得到了变形网格、位移增量分布、位移等值面分布等结果，探讨了系泊点位置与水平极限承载力之间的定量关系。计算表明，系泊点位置沿着吸力锚基础顶部到底部变化过程中，吸力锚的破坏趋势由向前倾覆破坏过渡到平动破坏，再转变为向后倾覆破坏，水平极限承载力先逐渐增大后逐渐减小。吸力锚平动破坏时，其周边土体被动土压力区面积取得最大值，此时水平极限承载力取得最大值。实际工程中应根据具体条件进行确定吸力锚基础的最优系泊点。

关键词：吸力锚基础;水平承载力;系泊点;位移增量;平动破坏

吸力锚是一种顶部封闭、底部开口的圆柱形薄壁结构，通过真空泵抽水使锚内外形成压力差而贯入海床中，类似一个倒扣在土中的“水桶”。吸力锚基础自上世纪90年代首次在挪威海上油田中成功应用以来，得到各国工程师的重视与发展。我国在1994年曹妃甸1-6两点系泊系统中首次成功使用吸力锚基础[1, 2]。与传统桩基础相比，吸力锚具有安装速度快、施工费用低、可重复利用、不受水深限制等优点，已逐步应用于海上风机、浮式结构、张力腿基础和立柱式平台中[3]。

在不同的海洋工程中，吸力锚的受力与破坏机制不尽相同。张力腿平台的结构浮力大于结构的自重，剩余浮力通过张力筋腱作用于吸力锚基础上，海水平稳时吸力锚主要承担上拔荷载[4, 5]；在浮式生产储油卸油船(FPSO)多点系泊系统中，系泊锚链一般呈半张紧状态，锚链与泥面多成夹角，此时吸力锚主要承担水平荷载[6, 7]；在海上风机或海上平台通过导管架与吸力锚相连的基础工程中，吸力锚主要承担竖向荷载、水平荷载与弯矩的组合荷载[8]。吸力锚基础的变形与破坏机理，显然与外荷载的加载方向有关。

王建华等[9]通过模型试验与有限元分析研究表明，对于在最佳系泊点受倾斜荷载作用的吸力锚，当加载方向大于20°时，锚的破坏表现为竖向拔出的模式，且锚底以下土层的反向承载力是影响其极限承载力的关键因素。张其一等[10]基于有限元方法对深海吸力锚的水平极限承载力进行了数值分析，给出的前倾转动破坏模式、平移滑动破坏模式以及后仰转动破坏模式， 较为合理地反映了系泊点位置对吸力锚稳定性的影响。Deng W[11]、EI-Sherbiny[12]、王志云[13]等从不同方面对吸力锚进行了深入研究。总体上看，一方面室内模型试验受到小比例尺寸的限制可能与实际有一定的差别，另一方面基于三维有限元分析的研究成果不丰富。

为此，本文拟基于三维有限元分析方法，对吸力锚基础承受水平荷载下的变形与承载特性进行系统研究，考察不同系泊点位置对承载力的影响，为吸力锚基础的设计与应用提供参考。

1三维有限元计算模型

吸力锚基础模型如图1所示，其直径为D=4.0 m、高度为L=12.0 m、厚度为t(钢结构)，水平作用力Fx作用在离顶部ηL的位置处。

现基于大型有限元计算软件Plaxis 3D建立吸力锚基础的有限元分析模型，如图2所示。为了减小边界条件的影响，计算模型的长、宽取10D，模型的高度取5L。模型采用10节点的三维四面体单元进行网格剖分。

图1　吸力锚基础构型

图2　吸力锚基础三维有限元计算模型

桶体一般为钢结构制作可视为线弹性体，弹性模量取E=2.1×108kPa，泊松比取v=0.21，厚度t=0.05 m。海床土为饱和软黏土，采用莫尔-库仑理想弹塑性模型进行模拟，其参数为：黏聚力c=6.3 kPa，内摩擦角φ=0°，弹性模量E=3000 kPa，泊松比v=0.35，饱和重度γsat=17.88 kN/m3。桶体与海床土体之间的摩擦通过设置接触面单元来实现。接触面单元采用参数Rinter来反映两者相互作用的程度，Rinter=[0, 1.0]。Rinter的具体取值可通过与试验数据的拟合试算确定，本次计算中取Rinter=0.7。

本文计算中，假定吸力锚已被施工、安置于海床土体中，施工扰动对海床土体的影响已结束，海床土体已恢复其原始物理力学参数，即暂不考虑施工过程对吸力锚承载特性的影响。

可采用位移控制法或荷载控制法进行加载。一般地，采用位移控制法能准确地得到吸力锚基础的荷载-位移曲线，当荷载-位移曲线的斜率接近于零时，表明在荷载不变的情况下吸力锚位移持续增大，据此可认为此时的地基已达到极限状态，与此对应的荷载就是吸力锚基础的极限承载力[14]。当然，采用荷载控制法时，当不同吸力锚承受相同的荷载时，吸力锚周边海床土体发生的位移越小，表明该类型的吸力锚承载力越大。

2吸力锚水平承载力分析

采用位移控制法来确定吸力锚基础的水平极限承载力，即在吸力锚作用点处施加一个位移值S(作用于y=0平面内)，通过有限元计算即可得到桶形基础的P-S曲线。该位移值不能过小，本处计算取S=0.5L(当S值过大时，有限元计算在未达到S值时出现计算不收敛而中断，但其对极限承载力的确定基本无影响)。

计算得到了水平荷载作用点变化情况，吸力锚基础达到极限平衡状态时的变形情况，如图3所示(网格变形放大5倍)。可见，水平荷载作用点η≤0.5(ηL≤6.0 m)时，吸力锚的破坏趋势是沿荷载方向向前倾覆破坏，且水平荷载作用点越靠近桶顶，向前倾覆破坏越容易；当水平荷载作用点η=0.58(ηL=7.0 m)时，吸力锚基本属于平动破坏，即整个吸力锚沿着荷载作用方向近似水平移动；当水平荷载作用点η≥0.67(ηL≥8.0 m)后，吸力锚的破坏趋势是沿荷载方向向后倾覆破坏，且水平荷载作用点越靠近桶底，向后倾覆破坏越容易。

即随着水平荷载作用点沿着吸力锚基础顶部到底部变化过程中，吸力锚的破坏趋势由向前倾覆破坏过渡到平动破坏，再转变为向后倾覆破坏。η=0向前倾覆破坏时，吸力锚基本沿着距桶底1/4高度处发生转动，并随着η值的增加转动点逐渐下移；η=1向后倾覆破坏时，吸力锚基本沿着距桶顶1/4高度处发生转动，并随着η值的减小转动点逐渐上移。该特征也可从后文的位移增量图中得到佐证。结合破坏形态，可进一步分析得吸力锚周围土体的主动、被动土压力区域分布情况。

图3　吸力锚基础受水平荷载后变形示意

水平荷载作用点变化情况下，吸力锚内部及周边土体的位移增量分布情况见图4。结合图3分析可知，吸力锚向前倾覆破坏时，吸力锚内中上部的土体及外侧中上部被动土压力区的土体产生了较大的位移，吸力锚内中下部的土体发生了旋转位移；吸力锚平动破坏时，吸力锚内部的土体及外侧被动土压力区的土体产生了较大的位移增量，且沿吸力锚高度范围内位移增量数值基本相等；吸力锚向后倾覆破坏时，吸力锚内中下部的土体及外侧中下部被动土压力区的土体产生了较大的位移，吸力锚内中上部的土体发生了旋转位移。

一般地，可认为旋转位移增量的中心点(位移增量为0)即是吸力锚倾覆破坏的旋转点。如图4(a)可见，η=0时吸力锚内中下部土体旋转位移的中心点大概距桶底1/4高度处，此即为荷载作用于桶顶时吸力锚基础的转动点；如图4(f)可见，η=1时吸力锚内中上部土体旋转位移的中心点大概距桶顶1/4高度处，此即为荷载作用于桶底时吸力锚基础的转动点。水平荷载作用点位置变化时，吸力锚基础的旋转点位置也发生相应变动。

图4　吸力锚受水平荷载后土体位移增量分布

平荷载作用点位置不同时，海床地基土的变形情况必然不相同，通过地基土的变形情况窥察吸力锚的变形与破坏趋势。不妨以海床地基土体位移为0.3 m的等值面来进行分析，如图5所示。可见，水平荷载作用于吸力锚中上部时，吸力锚中上部周边被动土压力压缩区、主动土压力坍塌区发生的位移比较大；ηL=7.0 m时吸力锚基本属于平动破坏，沿吸力锚高度范围内的周边土体均发生了较大的位移；水平荷载作用于吸力锚中下部时，吸力锚中下部周边被动土压力压缩区、主动土压力坍塌区发生的位移比较大，而基础顶部附近土体变形较小。

图5　吸力锚受水平荷载失效时土体位移为0.3 m的等值面

进一步得到了y=0平面内土体位移为0.3 m的等值线分布情况，如图6所示。一般地，水平荷载作用侧的土体为被动土压力区，相应另一侧为主动土压力区。故图6中两侧曲线主动、被动土压力区变形为0.3 m的等值线。特别地，吸力锚基础的水平承载力主要由被动土压力区土体的抗力组成。

基于位移控制法，可确定吸力锚基础的水平极限承载力。本文所提的水平极限承载力，是指吸力锚基础的水平荷载-位移曲线中，随着位移的增加水平荷载逐渐达到的恒定值，即视该恒定值为水平极限承载力。如ηL=0.0 m时的水平荷载-位移曲线见图7，水平荷载逐渐达到其恒定值1274 kN，故该情况下的水平极限承载力为1274 kN。

图6　y=0平面土体位移为0.3 m的等值线

图7　ηL=0.0 m时有限元计算得到的荷载-位移曲线

计算得到了水平荷载作用点变化情况下，吸力锚基础的水平极限承载力变化趋势，如图8所示。可见，随着水平荷载作用点从基础顶部移动到底部，吸力锚基础水平极限承载力先逐渐增大后逐渐减小，在η=0.58(ηL=7.0 m)时取得最大值。需要指出的是，水平极限承载力在η=0.58时取得最大值是在地基土均质条件下得到的，当海床土为非均匀的成层土时，该值将发生变化。

ηL=7.0 m时的水平极限承载力是ηL=0.0 m时相应值的2.84倍。可见，水平荷载作用位置(系泊点)对水平极限承载力有重要影响。同样的吸力锚基础、同样的海床地质条件，因锚索系泊点的位置不同而水平承载力不同。在最佳系泊点时，吸力锚基础的水平极限承载力取得最大值。

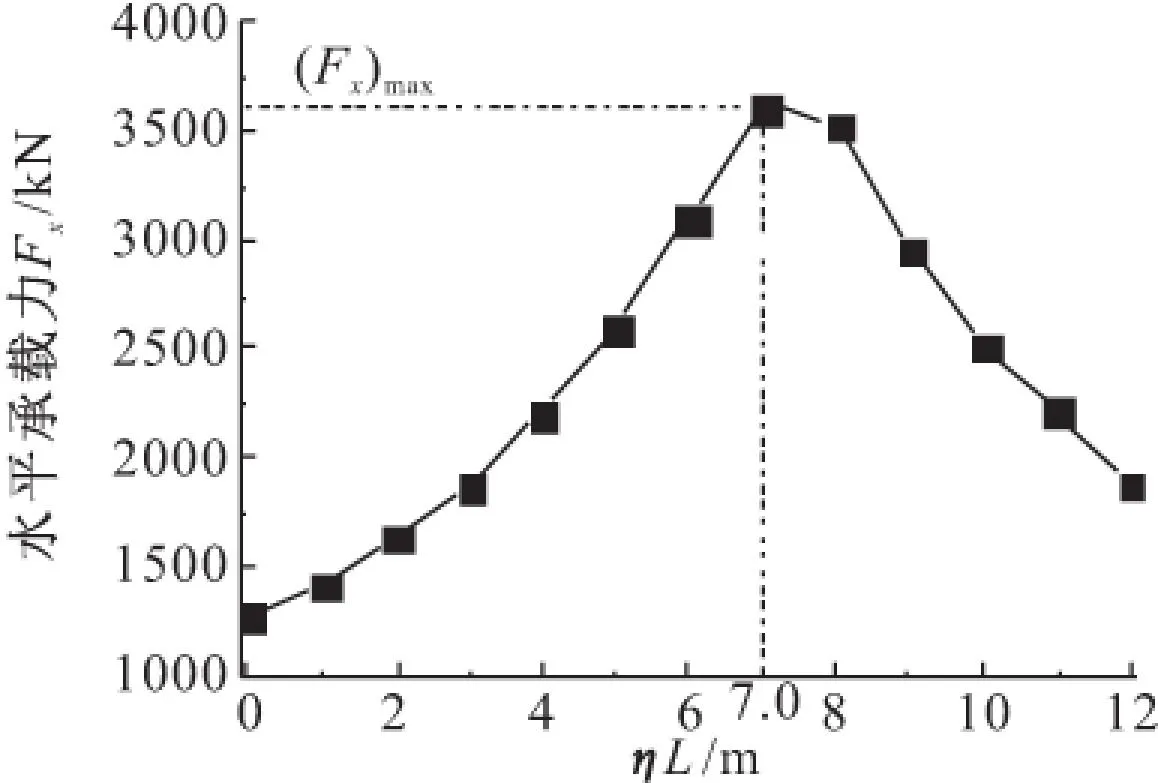
图8　荷载作用点对吸力锚水平极限承载力的影响

不同条件下的吸力锚基础的最佳系泊点位置也不尽相同。如韩智臣[3]等计算表明最佳系泊点在2L/3处，张其一[10]等研究表明最佳系泊点在(0.6～0.75)L处，本文算例表明最佳系泊点在0.58L处。工程中应根据具体条件进行计算，确定并选择承载力高的位置设置锚索系泊点。

现进一步分析最优系泊点时吸力锚的受力情况。根据图3(d)与图4(d)，本文算例最佳系泊点0.58L处吸力锚基础属于平动破坏，吸力锚内部及被动土压力区土体的位移增量基本相等。特别地，该情况下吸力锚内部全部土体基本属于被动土压力区，吸力锚系泊点一侧沿深度范围内的全部土体也基本属于被动土压力区，即平动破坏时被动压力区范围最大。桶基水平承载力主要由被动土压力区土体产生的抵抗反力构成，故被动土压力区面积大时其水平极限承载力也大。

吸力锚基础转动破坏时总有部分土体(旋转点附近)不属于被动压迫破坏(属于旋转剪切破坏)，如图4(a)与图4(f)所示，故其被动土压力区面积不是最大值。只有平动破坏时，吸力锚基础被动土压力区面积取得最大值。因此，寻找吸力锚的最优系泊点位置，实际上就是确定吸力锚基础处于平动破坏状态时的位置。即水平荷载位于最优系泊点时，吸力锚基础发生平动破坏。认识到这一点，对吸力锚基础的改进与发展有重要的促进作用。

鉴于问题的复杂性以及吸力锚基础的特殊性，本文上述研究成果还有待结合模型试验进行深入验证。或者说，模型试验可以在本文数值研究成果的基础上更好的设计与开展。

3结论

(1) 水平荷载作用点沿着吸力锚基础顶部到底部变化过程中，吸力锚的破坏趋势由向前倾覆破坏过渡到平动破坏，再转变为向后倾覆破坏。

(2) 吸力锚向前倾覆破坏时，吸力锚内中上部土体及外侧中上部被动土压力区的土体产生了较大位移，吸力锚内中下部土体发生了旋转位移；吸力锚平动破坏时，吸力锚内部土体及外侧被动土压力区的土体产生了较大位移增量，且沿吸力锚高度范围内位移增量数值基本相等；吸力锚向后倾覆破坏时，吸力锚内中下部土体及外侧中下部被动土压力区的土体产生了较大位移，吸力锚内中上部土体发生了旋转位移。

(3) 水平荷载作用点位置变化时，吸力锚基础的旋转点位置也发生相应变动。随着水平荷载作用点从吸力锚基础顶部移动到底部，吸力锚基础水平极限承载力先逐渐增大后逐渐减小。

(4) 水平荷载作用位置(系泊点)对水平极限承载力有重要影响。吸力锚平动破坏时，其周边土体被动土压力区面积取得最大值，此时水平极限承载力也取得最大值。故水平荷载的最优系泊点位置，就是吸力锚基础发生平动破坏的位置。

参考文献

[1]徐继祖, 史庆增, 宋安, 等. 吸力锚在国内近海工程中的首次应用与设计[J]. 中国海上油气(工程), 1995, 7(1): 32-36.

[2]徐继祖, 王翎羽, 陈星, 等. 从吸力锚到筒型基础平台——关于近海吸力式基础的工程经验和技术思考[J]. 中国海上油气(工程), 2002, 14(1): 1-5.

[3]韩智臣, 孙昭晨, 梁书秀. 饱和软黏土中吸力锚的承载能力数值分析[J]. 水运工程, 2013, (4): 162-167.

[4]董艳秋, 胡志敏, 张翼. 张力腿平台及其基础设计[J]. 海洋工程, 2000, 18(4): 63-68.

[5]Luke A M, Rauch A F, Olson R E, et al. Behavior of suction caissons measured in laboratory pullout tests [C]//ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2003: 839-847.

[6]张孝卫, 刘玉玺, 王江宏, 等. 用于FPSO系泊系统的吸力锚疲劳分析研究[J]. 船海工程, 2013, 42(6): 167-171.

[7]邹佳星, 任慧龙, 李陈峰. 极端海况下FPSO系泊系统安全性评估与分析[J]. 哈尔滨工程大学学报, 2015, 36(1): 104-108.

[8]Aubeny C P, Han S W, Murff J D. Inclined load capacity of suction caissons[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(14): 1235-1254.

[9]王建华, 刘晶磊, 陈文强. 加载方向对张紧式吸力锚极限承载力的影响分析[J]. 岩土工程学报, 2012, 34(3): 385-391.

[10]张其一, 董胜, 王青华. 深海吸力锚水平极限承载力研究[J]. 中国海洋大学学报(自然科学版), 2011, 41(5): 114-119.

[11]Deng W, Carter J P. A theoretical study of the vertical uplift capacity of suction caissons[J]. International Journal of Offshore and Polar Engineering, 2002, 12(2): 89-97.

[12]EI-Sherbiny R M. Performance of Suction Caisson Anchors in Normally Consolidated Clay[D]. Austin, TX: The University of Texas at Austin, 2005.

[13]王志云. 软土地基上吸力式沉箱基础的抗拔承载特性研究[D]. 大连: 大连理工大学, 2008.

[14]徐文强, 袁凡凡, 韦昌富, 等. 斜壁桶形基础承载特性的三维有限元分析[J]. 岩土工程学报, 2011, 33(s1): 485-490.

Horizontal Bearing Capacity of Suction Anchor Foundation in Ocean Engineering

LIUJin-long1,CHENLu-wang2,WANGJi-li3,WANGDong-lin4

(1.Department of Architecture Engineering, Hefei University, Hefei 230601, China; 2.School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China;3.Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China;4.School of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China.)

Abstract:Suction anchor can be used as the basis of deep sea mooring system, and its horizontal bearing capacity is related to the position of mooring point. Based on three-dimensional finite element method, the horizontal bearing capacity of suction anchor foundation in ocean engineering has been studied, the deformed mesh, incremental displacement, contour plane of displacement have been obtained, and the relationship between mooring point and horizontal ultimate bearing capacity of suction anchor foundation has been revealed. It is found that during the position of mooring point moving from the top of foundation to the bottom of foundation, the failure modes of suction anchor foundation changed from forward overturning to translational failure, and then backward overturning, and the value of horizontal ultimate bearing capacity of suction anchor foundation gradually increased firstly and then gradually reduced later. When suction anchor foundation reached the state of translational failure, the area of soil in passive earth pressure zone around suction anchor foundation reaches its maximum value, and the horizontal ultimate bearing capacity of suction anchor foundation reaches its maximum value. In engineering practice, the optimal position of mooring point of suction anchor foundation should be determined according to its specific conditions.

Key words：suction anchor foundation; horizontal bearing capacity; mooring point; displacement increment; translational failure

中图分类号：P754

文献标识码：A

文章编号：2095-0985(2016)02-0001-05

基金项目：国家自然科学基金(41306088); 安徽省自然科学基金(1308085ME61；1308085QE85)

作者简介：刘金龙(1979- ), 男, 江西宜丰人, 教授, 博士, 研究方向为岩土工程(Email: alnile@163.com)

收稿日期：2015-09-13修回日期： 2015-11-27