山区地形测绘中等高线的自动处理
2016-04-20于海乾王海波
于海乾 王海波
摘要:在山区地形测绘中我们需要对等高线进行计算机自动光滑与过滤处理,来提高作业效率。虽然我们日常使用南方公司基于AutoCAD二次开发的Cass软件有拟合与过滤功能,但它不能达到我们想要的效果,因此作者想到了另一种处理算法,下面我们来阐述这种算法。
关键词:等高线;光滑;过滤
一、等高线的光滑
光滑等高线有两个要求,第一是要保持等高线的原来位置不变,第二是不能有尖角。这是两个相互矛盾的要求,要满足这两个要求我们需要分两步走:
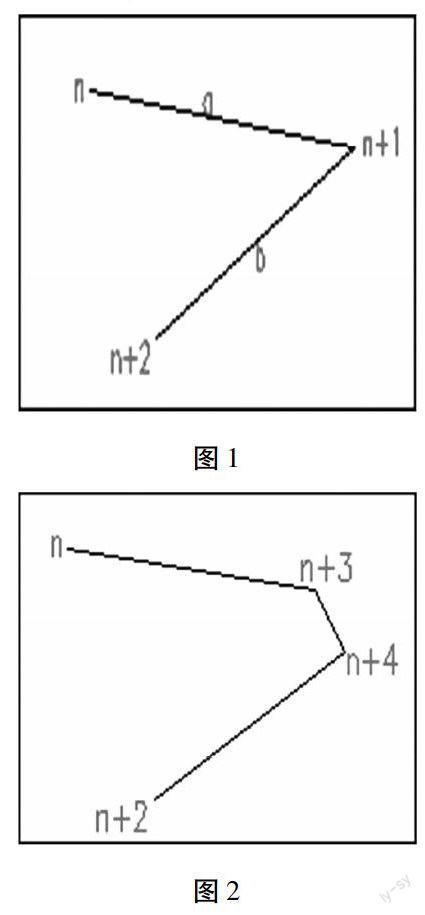
第一步:例如图1所示,我们还从等高线的当前点出发,设当前点为n,第二个点n+1,第三点n+2,设n点坐标X0,Y0;设n+1的坐标为X1,Y1;设n+2的坐标为X2,Y2;要把n+1点处的尖角去掉,取a边和b边中距离短的一边的四分之一(Dis),用这个距离作为参数求出n+1点附近处的两个点n+3,n+4。设n+3的坐标为X3,Y3;设n+4的坐标为X4,Y4.求n+3,n+4点坐标的公式如下:
X3=X0+(X1-X0)*dis/a
Y3=Y0+(Y1-Y0)*dis/a
X4=X2+(X1-X2)*dis/b
Y4=Y2+(Y1-Y2)*dis/b
說明一下:图2为去除尖角后的图,上面的“1/4”是个参数,作者在几次试验后发现用这个参数比较合理,既可以去掉尖角又不致超过限差的改变等高线的位置。在使用过程中我们可以多次使用此步,让等高线变得比较光滑。
第二步:使用3次B样拟合公式对等高线进行拟合处理,设等高线上的当前点为n,拟合公式为:
f0=1/6*(-T^3+3*T^2-3*T+1)
f1=1/6*(3*T^3-6*T^2+4)
f2=1/6*(-3*T^3+3*T^2+3*T+1)
f3=1/6*T^3
x=f0*Px(n)+f1*Px(n+1)+f2*Px(n+2)+f3*Px(n+3)
y=f0*Py(n)+f1*Py(n+1)+f2*Py(n+2)+f3*Py(n+3)
T为小于等于1的参数,计算公式为:i/m,其中”i”为从”0”到”m”的变量,”m”为要添加的节点数目。
Px为横坐标点数组,Py为纵坐标点数组。
x,y为光滑后的等高线上的节点坐标。
上面的算法已用程序实现,以下为主要部分源代码:
Sub CreateFittingLine()
Dim Sset As AcadSelectionSet
Dim filterType(0)As Integer
Dim filterData(0)As Variant
filterType(0)=0
filterData(0)="*line"
On Error Resume Next
If Not IsNull(ThisDrawing.SelectionSets.Item("Example"))Then
Set Sset=ThisDrawing.SelectionSets.Item("Example")
Sset.Delete
End If
Set Sset=ThisDrawing.SelectionSets.Add("Example")
Sset.SelectOnScreen filterType,filterData
Dim Obj As AcadEntity
Dim k As Integer
Dim a0,a1,a2,a3 As Integer '几个在闭合曲线中使用的参数
For k=0 To Sset.count-1
Set Obj=Sset.Item(k)
'3次B样拟合算法
Dim Px()As Double
Dim Py()As Double
Dim i,j,m,n As Integer
Dim T As Double
Dim f0,f1,f2,f3 As Double
Dim x,y As Double
Dim gc As Long '等高线的高程
m=GetVertexCount(Obj)-1
Dim Zb1()As Double
Dim Zb2()As Double
ReDim Zb1(2*m+1)As Double
For i=0 To m
Zb1(2*i)=Obj.Coordinate(i)(0)
Zb1(2*i+1)=Obj.Coordinate(i)(1)
Next i
Call changeOneRoleToFour(Zb1,Zb2)'去除距离太近的点‘可以通过改变此函数中的距离参数来提高线的圆滑,可是有可能照成点线不一。把尖角变成4个角
m=(UBound(Zb2)+1)/2-1 '现在有m+1个点
ReDim Px(m)As Double
ReDim Py(m)As Double
For i=0 To m
Px(i)=Zb2(2*i)
Py(i)=Zb2(2*i+1)
Next i
Dim Zb()As Double
'MsgBox Px(m)
n=-1
If Obj.Closed=False Then '不闭合的曲线与闭合的曲线处理起来是不一样的,先处理不闭合的曲线。
For j=0 To m-2
If j=0 Then '把起点带上
a0=j
a1=j
a2=j
a3=j
ElseIf j > m-3 Then '把终点带上
a0=m
a1=m
a2=m
a3=m
Else
a0=j
a1=j+1
a2=j+2
a3=j+3
End If
For i=0 To 3 '"3是个参数,参数越大等高线上节点越多"
T=i/3
f0=1/6*(-T^3+3*T^2-3*T+1)
f1=1/6*(3*T^3-6*T^2+4)
f2=1/6*(-3*T^3+3*T^2+3*T+1)
f3=1/6*T^3
x=f0*Px(a0)+f1*Px(a1)+f2*Px(a2)+f3*Px(a3)
y=f0*Py(a0)+f1*Py(a1)+f2*Py(a2)+f3*Py(a3)
n=n+1
ReDim Preserve Zb(2*n+1)As Double
Zb(2*n)=x
Zb(2*n+1)=y
Next i
Next j
ElseIf Obj.Closed=True Then '处理闭合曲线
For i=0 To 3 '"3是个参数,参数越大等高线上节点越多"
T=i/3
f0=1/6*(-T^3+3*T^2-3*T+1)
f1=1/6*(3*T^3-6*T^2+4)
f2=1/6*(-3*T^3+3*T^2+3*T+1)
f3=1/6*T^3
x=f0*Px(a0)+f1*Px(a1)+f2*Px(a2)+f3*Px(a3)
y=f0*Py(a0)+f1*Py(a1)+f2*Py(a2)+f3*Py(a3)
n=n+1
ReDim Preserve Zb(2*n+1)As Double
Zb(2*n)=x
Zb(2*n+1)=y
Next
Next j
End If '分闭合曲线与不闭合曲线
'gc=obj.Elevation
Dim Pts()As Double
Call ThreeFiltrates(Zb,Pts)'对生成的坐标过滤
Call AddNewdgx(Pts,Obj)
Obj.Delete
Next k
End Sub
二、等线的过滤:
CASS中也有等高线过滤的功能,即“复合线滤波”,但此功能并不能很好的完成既过滤掉等高线上多余的节点又保持等线的原来位置,例如当滤波值设小了过滤不完等高线上多余的节点;大了又改变了等高线的位置,如图1,图2所示。
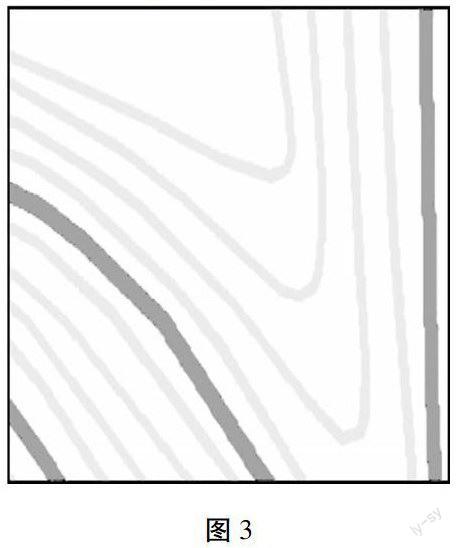
图3为过滤前的等高线。
于是作者想到了另一个算法即能过滤掉等高线上节点又能保持等高线位置。
我们从等高线的起点开始,设当前点为”n”,第二个为”n+1”,第三个为”n+2”,我们把三个点组成一个三角形,算出”n+1”点到底边的垂直距离”h”。我们可以设置一个参数,用于决定是否保留”n+1”点,当h大于這参数时去掉,小于时保留。计算”h”的公式:
h=2*area/c
area=s(s-a)(s-b)(s-c)
其中”area”为上面三角形的面积,”s”为三角形的周长,”a”为点”n”到”n+1”的边,”b”为”n+1”到”n+2”的边,”c”为点”n+2”到”n”的边。
此算法的好处在于可以保证等高线的位置不变又可以充分的过滤掉多余的节点,例如我们把参数设为“0.2”,等高线部分位置挪动0.2m,对等高线来说没有影响,但是却可以过滤掉绝大过多数多余的节点。
总结:
等高线的光滑中,第一步加点是为了保证使用拟合公式后等高线的位置不至移动太大,可以保持在正确的位置上同时初步光滑;第二步使用拟合公式拟合是让等高线完全光滑。大量的事实也证明这两步结合起来使用,等高线可以变得即光滑又能保证在原来的位置。使用拟合公式而不使用Cass的拟合功能是因为Cass的拟合功能改变了多段线的属性,我们在进一步整理等高线时会变得很不方便,使用拟合公式处理出来的等高线不但达到了比拟合功能更好的效果而且不改变等高线的性质,不影响进一步的处理工作。再使用过滤程序可以过滤后,等高线上多余节点被去掉而等高线位置不变。这样就达到我们所要的效果,在大面积山区测绘中对能明显提高内业的作业效率。
参考文献:
[1]《AutoCAD VBA二次开发教程》。