一种幅度信息辅助多伯努利滤波算法

袁常顺　　王　俊　　孙进平　　孙忠胜　　毕严先(北京航空航天大学电子信息工程学院　北京　100191)



一种幅度信息辅助多伯努利滤波算法

袁常顺王俊*孙进平孙忠胜毕严先
(北京航空航天大学电子信息工程学院北京100191)

摘要：在许多多目标跟踪场景中，目标返回的幅度通常强于虚警杂波返回的幅度。通过建立更加准确的包含幅度信息的目标和虚警杂波似然函数，可提高多目标估计精度。该文提出一种基于随机有限集的幅度信息辅助多伯努利滤波(Amplitude Information Assistant Multi-Bernoulli Filter，AIA-MBerF)算法。该算法通过建立幅度似然函数将幅度信息引入到多伯努利滤波的更新过程中，并给出针对线性和非线性模型的高斯混合(Gaussian Mixture，GM)和序贯蒙特卡洛(Sequential Monte Carlo，SMC)实现方法。仿真结果表明，该滤波算法相比于传统多伯努利滤波(Multi-Bernoulli Filter，MBerF)无论GM还是SMC实现都可获得更加准确稳定的目标数和对应的目标状态估计。关键词：多目标跟踪；随机有限集；幅度信息；多伯努利滤波

1　引言

多目标跟踪一直是目标跟踪领域研究的热点，其目的是从量测中联合估计时变且未知目标数和对应目标运动状态[1]。由于传感器自身特性，检测器提供给跟踪器的目标量测是不可靠的：一部分量测可能是杂波，一部分真实目标被漏检；跟踪器利用观测模型从量测中识别正确的目标，根据目标的运动状态模型跟踪目标。许多传感器，例如雷达和声呐，可同时实现对目标位置和幅度的测量。由于目标的信号幅度通常强于杂波，因此为区分量测来源于目标或者杂波提供了一个有价值的信息。在低信噪比目标跟踪中，将目标幅度信息作为一个量测变量与传统的距离、方位、多普勒等量测变量共同使用可提高数据关联，减少虚假航迹数目，取得更好的跟踪性能。目标幅度信息已经被应用于传统的多目标跟踪，如：概率数据关联(Probability Data Association，PDA)滤波器[2]、多假设跟踪(Multiple Hypothesis Tracking，MHT)[3]和Viterbi数据关联[4]。

传统的多目标跟踪方法围绕量测和目标的关联展开，随着目标数或者杂波数的增加，其计算量指数增长[1]。为了克服该困难，文献[1]以有限集统计学为基础，提出了随机有限集(Random Finite Set，RFS)方法，该方法为多目标跟踪问题提供了一个精确和简洁的公式表示，避免了数据关联，很快成为了多目标跟踪的研究热点之一。尤其是概率假设密度滤波器(Probability Hypothesis Density Filter，PHDF)[5]和势概率假设密度滤波器(Cardinalized Probability Hypothesis Density Filter，CPHDF)[6]的发展、实现[7-10]和收敛结果[11，12]已经证明了RFS方法的可行性。文献[13]将幅度信息应用于PHDF 和CPHDF，提高了多目标的跟踪精度。但是由于其SMC实现需要聚类处理，很难判断滤波性能的下降是由于聚类处理还是滤波器自身或者二者都有。不同于PHDF和CPHDF传递多目标阶矩和势分布，另一类基于RFS方法的多伯努利滤波器(MBerF)最近被提出，该滤波器传递近似后验多目标密度的多伯努利分布参数[1]。MBerF与PHDF具有相同的计算量，但是其SMC实现不需要采用聚类的方法估计多目标状态，计算量小于CPHDF。MBerF从提出后很快被成功的应用在许多实际问题中，例如：传感器网络跟踪[14]、音频跟踪[15]、虚拟跟踪[16]和图像跟踪[17]。

但是，到目前为止，所有关于MBerF的研究都没有考虑利用目标幅度信息提高多目标跟踪性能。基于此，本文从传统的MBerF出发，结合目标幅度信息，推导了一种幅度信息辅助多伯努利滤波(AIAMBerF)算法，该算法通过建立幅度似然函数将幅度信息引入到多伯努利滤波的更新过程中，充分利用杂波和目标幅度信息的不同，提高目标数和目标状态估计准确性。针对线性和非线性多目标跟踪场景，分别给出了GM和SMC实现。最后通过仿真实验验证了在已知信噪比(Signal-to-noise Ratio，SNR)和未知SNR下该滤波算法相比于传统MBerF在目标数和目标状态估计精度都得到显著提高。

2　幅度信息辅助多伯努利滤波算法

2.1 幅度模型

本文采用文献[2]中的瑞利分布描述杂波和目标幅度变化，该模型描述信号通过带通匹配滤波器，包络检波的幅度变化结果，同时对于Swerling 1和Swerling 2模型[18]也适用。杂波和目标幅度a的概率密度可分别被表示为[2]

其中，1+ S表示SNR的均值且

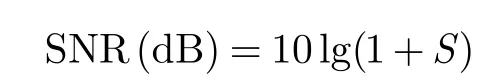
假设检测过程门限为τ＞0，检测概率和虚警概率分别为

通过门限检波器后，杂波和目标幅度a的概率密度可分别被表示为

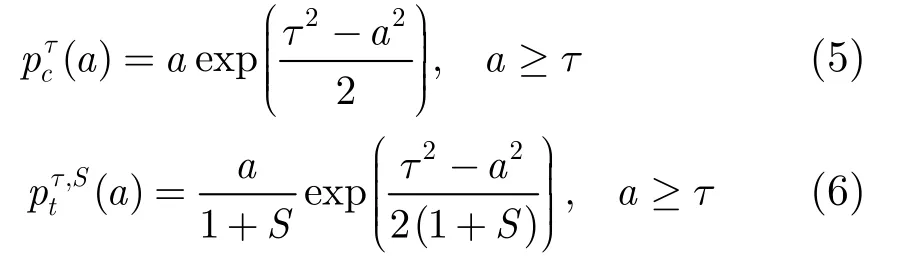
2.2 幅度似然函数

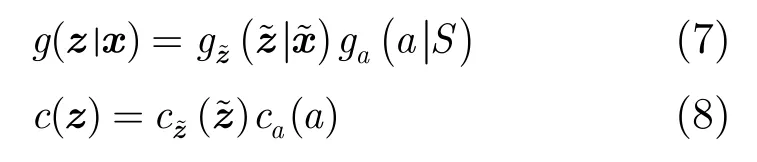
(1)已知SNR：当SNR已知时，检测门限τ通过给定虚警值计算，检测概率值利用式(3)解析求解。采用式(5)和式(6)作为检测后杂波和目标的幅度似然函数。

(2)未知SNR：在实际应用中，SNR通常是未知的，本文采用文献[13]的方法，通过排除参数S所有可能取值范围，找到一个不依赖参数S的目标幅度似然函数ga。对于瑞利幅度似然函数，假设先验的SNR在dB域服从均匀分布，参数S对应的取值范围为，则该目标幅度似然函数可表示为

2.3 幅度信息辅助多伯努利滤波（AIA-MBerF）

由于杂波和目标幅度信息不同且可测，本文推导了一种AIA-MBerF算法，该算法通过建立幅度似然函数将幅度信息引入到多伯努利滤波的更新过程中，提高目标数和目标状态估计准确性。其预测和更新步骤总结如下：

预测假设在k -1时刻，后验多目标密度为多伯努利形式[19]：

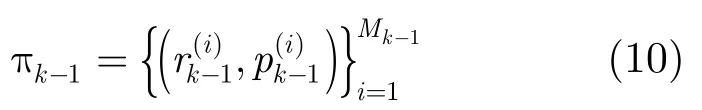
则预测的多目标密度也为多伯努利形式，且由存在和新生两部分组成，即[19]

更新假设在k时刻，预测的多目标密度为多伯努利形式：

则给定量测集Zk下，后验多目标密度近似为多伯努利形式，由遗留和更新两部分组成：

3　滤波器实现

本节详细给出了线性模型的GM-AIA-MBerF和非线性模型的SMC-AIA-MBerF实现。

3.1 GM-AIA-MBerF实现

假设目标的状态转移和量测采用线性高斯模型，其表示为

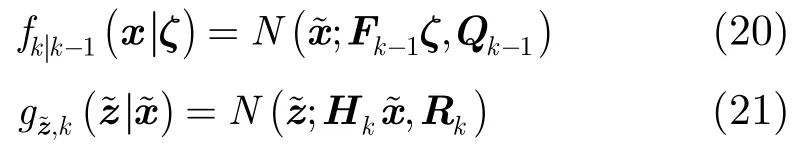
GM-AIA-MBerF实现主要包含预测、更新、剪枝和多目标状态提取步骤，详细过程如下：

更新假设在k时刻，预测的多目标密度为如下多伯努利形式：

则给定量测集Zk下，更新的后验多目标密度式(15)计算如式(24)～式(27)：

其中，

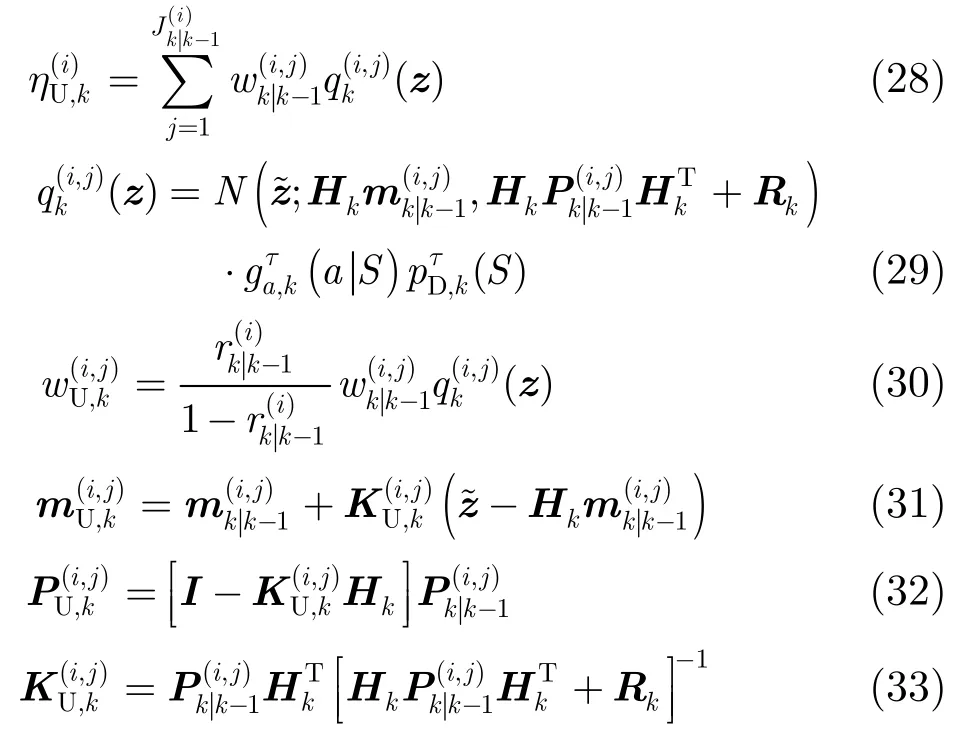
剪枝由于在预测过程中新生目标的加入和更新过程中平均多伯努利项的增加，使得最终表示多伯努利后验密度的高斯数目不断增加。为了降低高斯数目，采用文献[19]中的方法，首先删除存在概率低于门限P的多伯努利项；其次对于保留的多伯努利项，删除高斯权重低于门限T的高斯分量，同时合并距离在U范围内的高斯分量。

多目标状态提取类似于文献[19]的方法，首先估计出目标数，然后选取对应数目的存在概率最大的伯努利项，计算其高斯分量的均值作为对应目标状态。

3.2 SMC-AIA-MBerF实现

由于SMC-AIA-MBerF是直接采用标准的SMC方法，因此该滤波器的收敛结果与文献[20]中的收敛结果相一致。其预测、更新、重采样和多目标状态提取步骤如下：

更新假设在k时刻，预测的多目标密度为式(34)，式(35)所示的多伯努利形式：

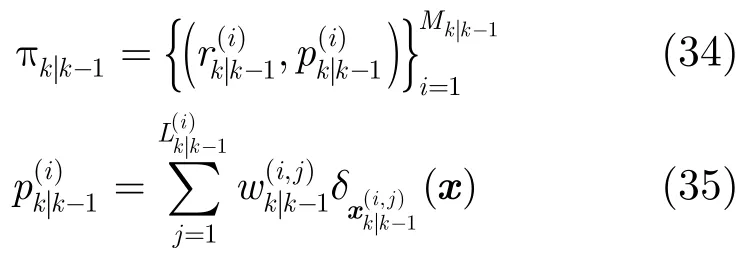
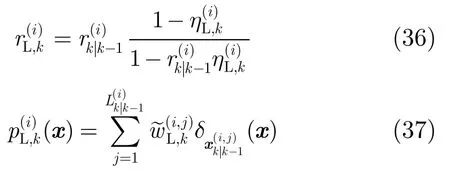
其中

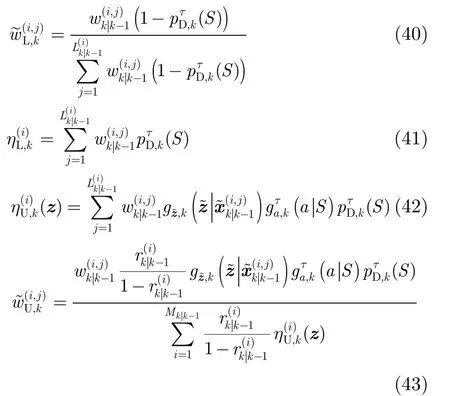
重采样由于在预测过程中新生目标的加入和更新过程中平均多伯努利项的增加，使得最终近似后验密度的多伯努利项数目不断增加。采用文献[19]的方法，删除存在概率低于门限值P的伯努利项，同时设置一个允许存在的最大多伯努利项数Tmax。

多目标状态提取类似于标准的多伯努利滤波器对于多目标状态的提取[19]，首先采用后验势分布的均值估计目标数，然后选取对应数目的存在概率最大的伯努利项，计算其后验密度的均值作为对应目标状态。

4　仿真实验与分析

4.1 线性模型GM-AIA-MBer实现

考虑一个二维线性多目标跟踪场景，仿真场景中共有12个目标作匀速运动，初始时刻有3个目标作匀速运动，随后分别有9个新生目标出现。目标的运动模型和量测模型分别为

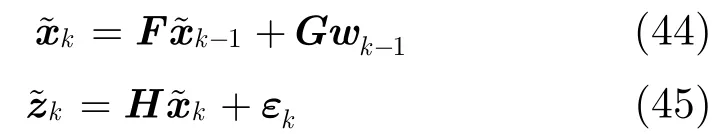
图1(b)和图1(c)给出了已知和未知SNR条件下，GM-AIA-MBerF单次仿真实验对多目标位置的估计结果。从仿真结果可以看出无论在已知或者未知SNR条件下，给出的算法均可在大量虚警杂波中正确跟踪单独目标运动和不同的目标新生和消失。

为进一步分析GM-AIA-MBerF在SNR已知和未知条件下的性能，将其与标准GM-MBerF对比。图2展示了GM-MBerF，SNR已知和未知条件下GM-AIA-MBerF经100次蒙特卡洛仿真实验平均后的多目标个数估计及方差随时间变化曲线。从图中可以看出，无论是已知或未知SNR的GM-AIAMBerF目标数估计性能都优于标准的GM-MBerF，并且已知和未知SNR的GM-AIA-MBerF性能接近。标准的MBerF会存在偏差，这是由于标准的MBerF主要应用于低杂波高检测概率的环境，对于GM实现，其适用范围为杂波强度小于20的泊松分布和检测概率高于0.9的场景[19]，当杂波数增多时会存在估计偏高。而GM-AIA-MBerF算法由于增加了幅度信息，可以很好提高对杂波和目标的区别，因此其对于高杂波环境效果好，但是由于没有改进MBerF滤波器本身的算法结构，因此对于低检测概率环境效果仍然不理想。

最优子模式分配(Optimal SubPattern Assignment，OSPA)距离[21]用于定量分析算法的估计误差，定义如式(46)：

图3展示了经100次蒙特卡洛仿真实验平均后得到的三者OSPA距离随时间变化曲线。该结果进一步验证了GM-AIA-MBerF性能优于标准的GMMBerF。这是因为目标和杂波的幅度分布不同，通过采用幅度信息量测有利于区分目标和杂波，提高对杂波的抑制能力，更好地估计真实目标数。

图1　包含杂波量测和GM-AIA-MBerF估计结果

图2　3种滤波器的目标数估计均值与方差

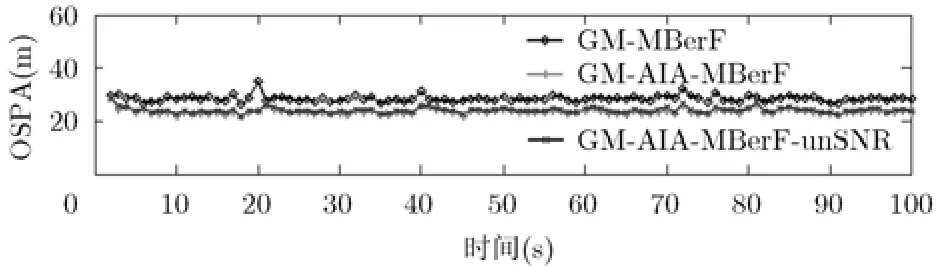
图3　3种滤波算法的OSPA距离

表1所示为不同虚警概率和SNR下，3种滤波器的平均OSPA距离。可以看出，随着SNR的提高，3种滤波器的OSPA距离呈现整体下降趋势，这主要是由于随着SNR的提高，检测概率提高，目标漏检降低；同时已知或未知SNR的GM-AIAMBerF的性能比较接近，均优于未利用幅度信息标准GM-MBerF，且SNR越高优势越明显，这主要是由于利用幅度信息之后，提高了对虚假目标的识别能力，可以更加有效地消除杂波干扰。另一方面，随着虚警概率的降低，3种滤波器的OSPA距离呈现整体上升趋势，这是由于随着虚警概率的降低，目标检测概率降低，而MBerF算法对于检测概率更加敏感，因此在仿真中出现了OSPA距离上升的结果。

4.2 非线性模型SMC-AIA-MBerF实现

采用一个非线性多目标运动场景来验证SMCAIA-MBerF性能。观测区域是半径为2000 m的半圆区域，监控时间为100 s，传感器位于原点，采样间隔1 s。总共有10个起始时刻和消失时刻不同的目标出现在该场景中。真实目标按照直角转弯模型运动，目标运动状态变量由位置、速度变量和转弯率ωk组成。状态转移模型为

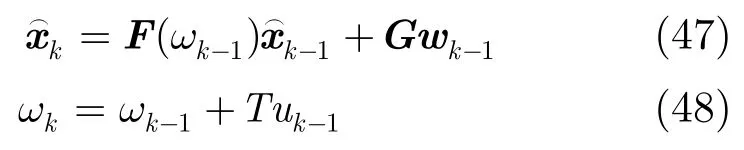
其中

表1　不同信噪比和虚警率下的OSPA距离

图4(b)和图4(c)给出了已知SNR和未知SNR条件下，采用SMC-AIA-MBerF单次仿真实验对多目标位置的估计结果。从仿真结果可以看出无论在已知SNR或者未知SNR条件下，给出的滤波均可在大量虚警杂波中正确跟踪单独目标运动和不同的目标新生和消失。

图5展示了已知和未知SNR的SMC-AIAMBerF和 SMC-MBerF经100次蒙特卡洛仿真实验平均后的多目标个数估计及其方差随时间变化曲线，其结果与GM实现结果类似。

图6展示了经100次蒙特卡洛仿真实验平均后得到的三者OSPA距离随时间变化曲线。表2所示为不同虚警概率和SNR下，3种滤波算法的平均OSPA距离，其结果与GM实现结果类似。

5　结论

由于在多目标跟踪场景中，目标和虚警杂波返回的信号幅度不同，该幅度信息可以作为一种有效的辅助，提高跟踪性能，消除虚警杂波。因此，本文提出了一种基于随机有限集的幅度信息辅助多伯努利滤波算法，该算法通过建立幅度似然函数将幅度信息引入到多伯努利滤波的更新过程中。针对线性和非线性模型，给出了GM和SMC实现方法。仿真结果表明，该算法相比传统MBerF，无论GM还是SMC实现都可获得更加准确稳定的目标数和对应的目标状态估计。

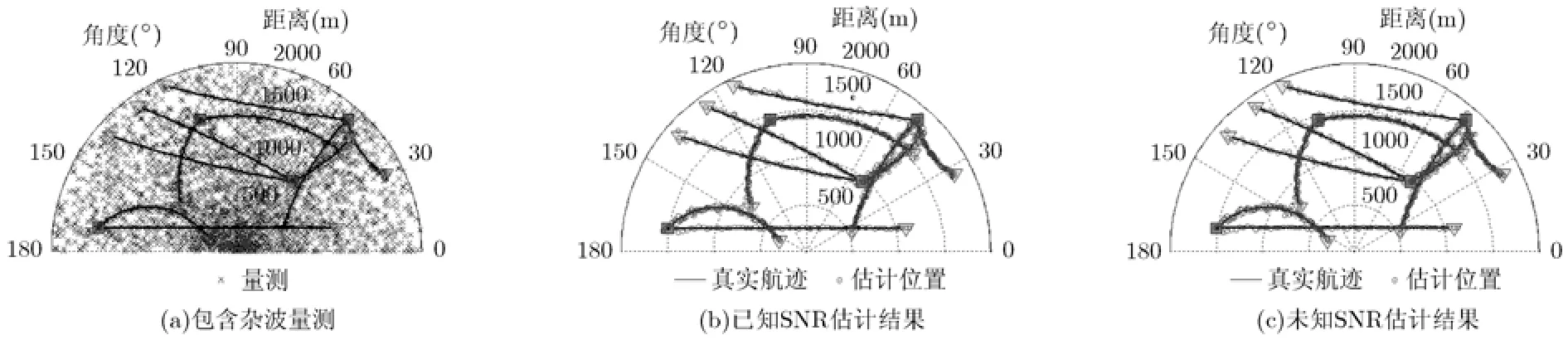
图4　包含杂波量测和SMC-AIA-MBerF估计结果

图5　3种滤波算法的目标数估计均值与方差

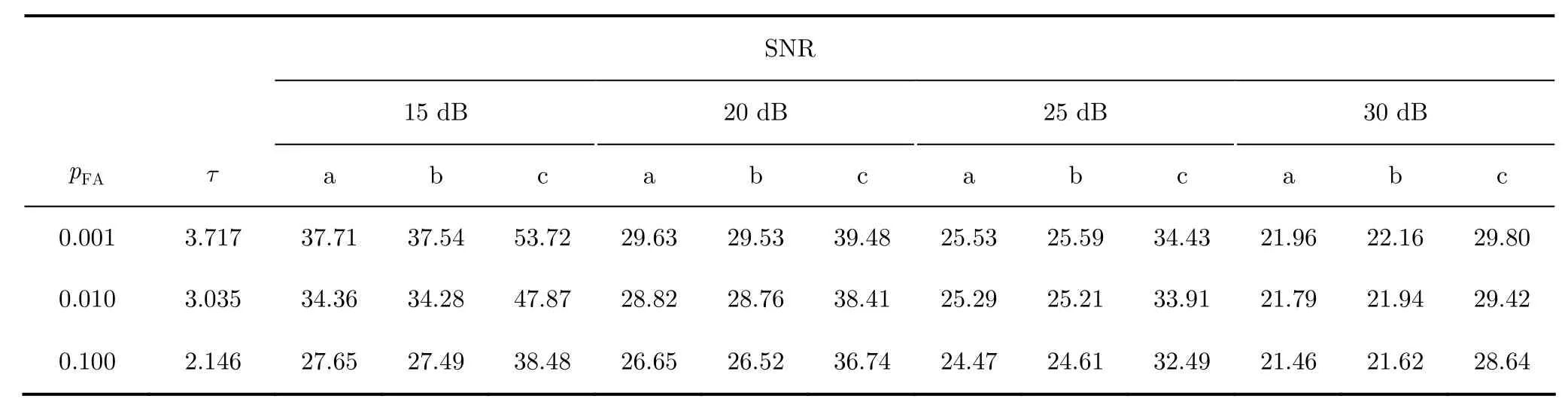
表2　不同信噪比和虚警率下的OSPA距离

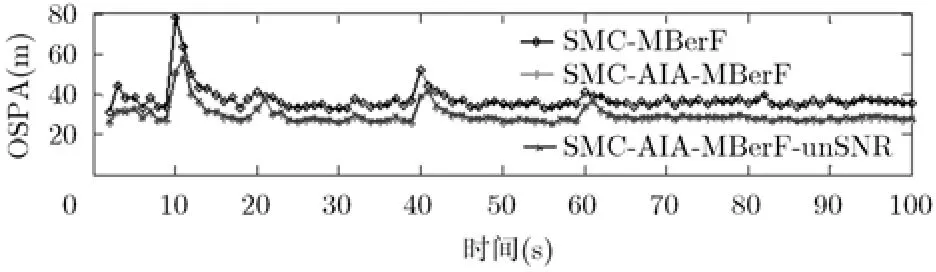
图6　3种滤波算法的OSPA距离

参考文献

[1]MAHLER R.Statistical Multisource-Multitarget Information Fusion[M].Norwood:Artech House，2007:565-682.

[2]LERRO D and BAR-SHALOM Y.Automated tracking with target amplitude information[C].American Control Conference，USA，San Diego，1990:2875-2880.

[3]VAN KEUK G.Multihypothesis tracking using incoherent signal-strength information[J].IEEE Transactions on Aerospace and Electronic Systems，1996，32(3):1164-1170.

[4]LA Scala B F.Viterbi data association tracking using amplitude information[C].Proceedings of the 7th International Conference on Information Fusion，Stockholm，Sweden，2004:698-705.

[5]MAHLER R.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39(4):1152-1178.

[6]MAHLER R.PHD filters of higher order in target number[J].IEEE Transactions on Aerospace and Electronic Systems，2007，43(4):1523-1543.

[7]VO B N and MA W.The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2006，54(11):4091-4104.

[8]VO B T，VO B N，and CANTONI A.Analytic implementations of the cardinalized probability hypothesis density filter[J].IEEE Transactions on Signal Processing，2007，55(7):3553-3567.

[9]胡子军，张林让，张鹏，等.基于高斯混合带势概率假设密度滤波器的未知杂波下多机动目标跟踪算法[J].电子与信息学报，2015，37(1):116-122.doi:10.11999/JEIT140218.HU Zijun，ZHANG Linrang，ZHANG Peng，et al.Gaussian mixture cardinalized probability hypothesis density filter for multiple maneuvering target tracking under unknown clutter situation[J].Journal of Electronics ＆ Information Technology，2015，37(1):116-122.doi:10.11999/JEIT140218.

[10]占荣辉，刘盛启，欧建平，等.基于序贯蒙特卡罗概率假设密度滤波的多目标检测前跟踪改进算法[J].电子与信息学报，2014，36(11):2593-2599.doi:10.3724/SP.J.1146.2013.02029.ZHAN Ronghui，LIU Shengqi，OU Jianping，et al.Improved multitarget track before detect algorithm using the sequential monte carlo probability hypothesis density filter[J].Journal of Electronics ＆ Information Technology，2014，36(11):2593-2599.doi:10.3724/SP.J.1146.2013.02029.

[11]CLARK D and BELL J.Convergence results for the particle PHD filter[J].IEEE Transactions on Signal Processing，2006，54(7):2652-2661.

[12]CLARK D and VO B T.Convergence analysis of the Gaussian mixture PHD filter[J].IEEE Transactions on Signal Processing，2007，55(4):1204-1212.

[13]CLARK D，RISTIC B，VO BN，et al.Bayesian multi-object filtering with amplitude feature likelihood for unknown object SNR[J].IEEE Transactions on Signal Processing，2010，58(1):26-37.

[14]GOSTAR A K，HOSEINNEZHAD R，and BABHADIASHAR A.Sensor control for multi-object tracking using labeled multi-Bernoulli filter[C].The 17th International Conference on Information Fusion，Salamanca，2014:1-8.

[15]CHONG N，WONG S，NORDHOLM S，et al.Multiple sound source tracking and identification via degenerate unmixing estimation technique and cardinality balanced multi-target multi-bernoulli filter(DUET-CBMeMBer)with track management[C].Asia-Pacific Signal and Information Processing Association，Siem Reap，2014:1-5.

[16]KIM D Y and JEON M.Robust multi-Bernoulli filtering for visual tracking[C].International Conference on Control，Automation and Information Sciences(ICCAIS).Gwangju，2014:47-51.

[17]胡子军，张林让，房嘉奇.多站无源雷达多起伏目标检测前跟踪算法[J].电子与信息学报，2015，37(3):651-657.doi:10.11999/JEIT140466.HU Zijun，ZHANG Linrang，and FANG Jiaqi.A Trackbefore-detect algorithm for tracking multiple fluctuating targets using passive multistatic radar[J].Journal of Electronics ＆ Information Technology，2015，37(3):651-657.doi:10.11999/ JEIT140466.

[18]SKOLNIK M I.Introduction to Radar[M].New York:McGraw-Hill，2002:148-256.

[19]VO B T，VO B N，and CANTONI A.The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J].IEEE Transactions on Signal Processing，2009，57(2):409-423.

[20]LIAN F，LI C，HAN C，et al.Convergence analysis for the SMC-MeMBer and SMC-CBMeMBer filters[J].Journal of Applied Mathematics，2012，2012:1-25.

[21]SCHUHMACHER D，VO B T，and VO B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing，2008，56(8):3447-3457.

袁常顺：男，1987年生，博士生，研究方向为雷达信号处理、随机集多目标跟踪等.

王俊：男，1972年生，教授，博士生导师，研究方向为雷达信号处理、实时信号处理等.

孙进平：男，1975年生，教授，博士生导师，研究方向为高分辨率雷达信号处理、压缩感知等.

孙忠胜：男，1980年生，博士生，工程师，研究方向为雷达信号处理、目标识别等.

毕严先：男，1988年生，博士生，研究方向为雷达信号处理、3维成像等.

A Multi-Bernoulli Filtering Algorithm Using Amplitude Information

YUAN ChangshunWANG JunSUN JinpingSUN ZhongshengBI Yanxian
(School of Electronics and Information Engineering，Beihang University，Beijing 100191，China)

Abstract:In many multi-target tracking scenarios，the amplitude of target returns are stronger than those coming from false alarms.This amplitude information can be used to improve the multi-target state estimation by obtaining more accurate target and false-alarm likelihoods.In this paper，a novel multi-Bernoulli filtering algorithm is proposed，which is based on the random finite set and incorporate the amplitude information.The amplitude likelihood functions are derived to incorporate the amplitude information into the multi-Bernoulli filter in the update step.In addition，a Gaussian Mixture(GM)implementation for the linear model and a Sequential Monte Carlo(SMC)implementation for the non-linear model are proposed.Simulation results for Gaussian Mixture and Sequential Monte Carlo implementations show that the proposed filter demonstrates a significant improvement than conventional multi-Bernoulli filter in the estimation accuracy of both the number of targets and their states.

Key words:Multi-target tracking; Random finite set; Amplitude information; Multi-Bernoulli filter

基金项目：国家自然科学基金(61171122，61201318，61471019，61501011)，中央高校基本科研业务费专项资金(YWF-15-GJSYS-068)

*通信作者：王俊yuanchang61@126.com

收稿日期：2015-06-08；改回日期：2015-11-11；网络出版：2015-12-18

DOI:10.11999/JEIT150683

中图分类号：TN953

文献标识码：A

文章编号：1009-5896(2016)02-0464-08

Foundation Items:The National Natural Science Foundation of China(61171122，61201318，61471019，61501011)，The Fundamental Research Funds for the Central Universities(YWF-15-GJSYS-068)