基于BDS/GPS的短基线单历元多频RTK定位研究

谢建涛,郝金明,于合理,田英国,张宇

(信息工程大学导航与空天目标工程学院,郑州 450052)



基于BDS/GPS的短基线单历元多频RTK定位研究

谢建涛,郝金明,于合理,田英国,张宇

(信息工程大学导航与空天目标工程学院,郑州 450052)

摘要：随着全球卫星导航系统(GNSS)进入多系统时代,天空中导航卫星的可见数不断增加,而我国北斗卫星导航系统(BDS)也已开始面向用户提供三频导航信号,为整周模糊度的解算提供有利条件,极大改善了GNSS单历元RTK定位的精度和可靠性。本文在基于几何的(TCAR)算法的基础上,将BDS/GPS组合引入到宽巷和窄巷模糊度解算中,提出一种基于双系统组合的单历元多频RTK定位模型,通过实验进行论证分析,结果表明：该模型在模糊度解算效率和定位精度两个指标方面都优于其他两种模型。

关键词：BDS/GPS;TCAR;多频RTK;模糊度解算

0引言

GNSS工程应用时,城市高楼密集区和位于深山峡谷等环境下采用单卫星系统进行定位时,受到地形及周围环境的影响,用户接收机可见的卫星数目少且分布不佳,导致系统的可用性降低,无法满足定位的最低要求[1]。多系统条件下,可见卫星的增加为解决上述问题提供了可能。以北斗/GPS 联合RTK定位为例,其可见卫星数增加将近一倍,可显著增强RTK定位模型的几何强度,进而可缩减RTK定位的初始化时间并提高其可靠性[2]。

GNSS单历元RTK定位精度和可靠性取决于模糊度能否正确固定[3]。在GNSS单系统条件下,当天空中的可见导航卫星数很少时,整周模糊度的计算就不能够完成。2012年底,我国的北斗卫星导航系统已部署完成由5颗GEO卫星、5颗IGSO卫星和4颗MEO卫星组成的区域星座,具备了向中国及周边地区提供服务的能力。文献[4]和[5]都对北斗卫星导航系统的进展及贡献进行了详细的阐述。多个卫星导航系统的投入运行使得天空中导航卫星的可见数增加,对整周模糊度的解算提供有利条件。

GPS和BDS在信号体制结构方面采用的都是码分多址技术(CDMA),使得两者在数据处理模型方面非常接近,有利于进行双系统组合定位。文献[6]对BDS/GPS组合相对定位的数学模型和时空基准统一问题进行了研究。基于双频数据,文献[3]通过采用无几何模型依次固定宽巷模糊度和窄巷模糊度,对短基线BDS/GPS组合单历元RTK定位进行了研究。文献[7]针对不同高度角条件下的BDS/GPS联合RTK定位性能进行了分析，文献[8]中采用Kalman滤波模型对BDS/GPS组合多频数据进行处理，研究表明，若直接固定窄巷模糊度，BDS三频数据相较于双频数据并无明显优势，且模糊度参数的增加也会造成很大的计算压力。

基于三频观测的TCAR算法通过对原始载波相位观测量进行线性组合,可得到长波长、弱电离层延迟、弱观测噪声的最优虚拟观测量,按波长从长到短,依次固定超宽巷、宽巷和窄巷模糊度,可明显提高模糊度解算效率。文献[9]和[10]结合GPS数据对TCAR算法进行了优化。文献[11]和[12]针对BDS的三频特性进行了分析，文献[13]鉴于TCAR算法的优越性以及多系统组合定位的优势,本文在基于几何的TCAR算法的基础上,对BDS/GPS组合单历元多频RTK定位的数学模型进行了研究,并结合实验数据进行了论证分析,得出了有益的结论。

1时间与坐标系统的统一

时间系统和坐标系统是导航定位的参考基准,任何形式的导航定位都是在一定的时间和坐标框架内进行[6,14]。

1.1时间系统

GPS时间系统(GPST) 属于原子时系统(AT),其秒长与原子时相同,但与国际原子时(TAI) 具有不同的原点,任一瞬间GPST与TAI间均有一常量偏差(19 s),GPST与TAI的关系式为

GPST=TAI-19 s.

(1)

TAI 与 UTC的关系式为

TAI=UTC+1 s×n，

(2)

式中,n为TAI与 UTC 间不断调整的参数。由上面的两式可以得到GPST与UTC(USNO)之间的关系

GPST=UTC(UCNO)+1s×n-19s.

(3)

BDS时间基准采用北斗时(BDT),与GPS时间系统(GPST) 间存在14s的整数差,BDT与中国维持的协调世界时UTC(NTSC)之间的关系式为

BDT=UTC(NTSC)+1s×n-19s-14s.

(4)

通过对GPS、BDS时间框架的分析,它们的时间基准都能和UTC形成一定的联系,将UTC作为中间变量,可实现不同时间系统的统一。实际上,目前许多GNSS混合观测文件包含了多个系统的数据,且统一采用GPST作为观测时间系统,因此,这部分转换通常可省去。

1.2坐标系统

最新的WGS-84(G1674)坐标系于2012年2月8日投入使用,和最新的ITRF08保持一致。CGCS2000定义为ITRF97,采用2 000.0历元下的坐标和速度场。WGS-84与CGCS2000都与ITRF存在一定的关系,它们之间的转换,本质上是在不同的ITRF框架间实现统一[14]。相关研究表明,对于北斗和GPS联合相对定位,基本不需要考虑坐标系统差造成的影响[8]。

2BDS/GPS组合差分定位模型

在短基线(<20 km)条件下,忽略双差对流层残差、双差电离层残差以及轨道误差的影响,载波和伪距差分定位的数学模型为[7]

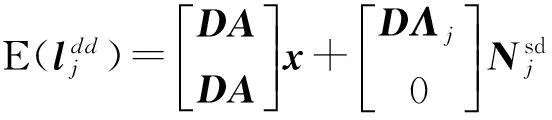
(5)

式中: sd表示单差; dd表示双差; Λj=

(6)

由单差模糊度参数到双差模糊度参数的转换矩阵表示为

(7)

3多频模糊度解算

三频情形下,频率的多样性可以提高无几何模糊度解算方法的可靠性。就无几何模糊度解算效果而言,三频要明显优于双频。但是,无几何条件下观测噪声和电离延迟误差对窄巷模糊度解算造成的影响非常敏感[17-18],依然制约着模糊度解算的收敛速度和可靠性。因此,对于多系统多频情形,鉴于基于整数最小二乘估计的几何模糊度解算方法可以将模糊度固定成功率最大化,其仍然是模糊度解算的第一选择[8]。

本文在基于几何的TCAR模型的基础上,提出了基于GPS双频数据和BDS三频数据的多频模糊度解算(MCAR)算法。短基线条件下,忽略双差电离层延迟和双差对流层延迟的影响,基于几何的TCAR和MCAR模型可描述为以下几种。

3.1超宽巷(EWL)模糊度解算

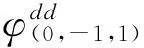
(8)

3.2宽巷(wide-lane,WL)模糊度解算

对于BDS单系统下的TCAR算法,WL12载波的双差观测方程为

(9)

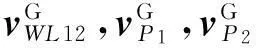
(10)

3.3窄巷模糊度(NL)解算

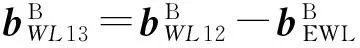
对于BDS单系统条件下的TCAR算法,NL载波的双差观测方程为

(11)

对于MCAR算法,采用GPS双频数据与BDS三频数据组合定位时,NL载波的双差观测方程为

(12)

第二步中WL模糊度估计采用直接取整的方式时成功概率较低,导致最终估计可靠性不高。因此,在第二步中固定WL模糊度时采用基于几何的观测模型,使用接收机与卫星之间的空间几何约束信息,由于顾及所有观测量信息和模糊度之间的相关信息,该算法优于无几何模型。

EWL和WL模糊度解算采用经典最小二乘估计法,短基线条件下其固定成功率是非常高的,且计算量要比Kalman滤波算法小的多。对于NL模糊度解算,MCAR算法只解算B1和L1频点上的载波相位模糊度参数,相较于非组合情况下直接求解B1、B2、B3、L1以及L2频点上的载波相位模糊度参数,前者模糊度参数的维数仅为后者的2/5,当采用Kalman滤波计算浮点解以及LAMBDA算法对浮点解进行固定时,计算压力都要小很多,计算效率也更高。

总的来看,相较于BDS/GPS组合直接解算窄巷模糊度,MCAR算法兼具了TCAR算法的优点,通过对原始载波相位观测量进行线性组合,得到长波长、弱电离层延迟、弱观测噪声的最优虚拟观测量,按波长从长到短,采用不断精化的伪距观测量依次固定EWL、WL和NL模糊度,可明显提高NL模糊度解算效率。此外,就计算量而言,MCAR算法也更优,可以有效缓解实时计算时造成的计算压力。

相较于TCAR算法,MCAR算法将BDS/GPS组合引入到宽巷和窄巷模糊度解算中,实现了由单系统条件到双系统条件的拓展,采用的观测量更多,星座几何结构更优,定位可靠性更高。此外,双系统组合定位能够有效改善BDS单系统条件下由于特殊星座设计等原因造成的定位精度方面的缺陷。

4实验分析

为验证MCAR模型的有效性和可行性,本文采用了三组静态基线数据进行实验,数据采集使用司南多模接收机,卫星高度截止角设为15°,如表1所示。

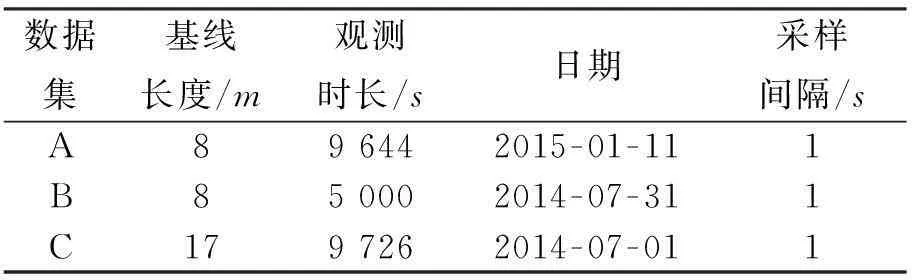
表1　采用的数据集概况

将GPS双频数据与BDS三频数据组合直接解算NL记为BDS/GPS模型,并与BDS单系统TCAR模型以及基于双系统组合的MCAR模型就模糊度解算和定位精度两个指标进行比对分析。解算过程均采用单历元模糊度固定模式,其优点是解算结果不受载波相位周跳的影响[7]。

EWL和WL模糊度固定ratio阈值rE和rW均设为2,而NL模糊度固定ratio阈值rN则分别设为2、3和5,以比较BDS/GPS、TCAR和MCAR三种不同模式下NL模糊度解算(AR)效率。由于EWL或WL模糊度固定失败都会造成NL模糊度无法解算,因此本文只需对NL模糊度解算效率进行比较。统计结果如表2～表4所示。表2中,对于数据集A中8m超短基线,ratio阈值为2、3和5时,三种模式NL模糊度固定成功率均达到100%,效果相同。表3中,对于数据集B,基线长度为8km,ratio阈值为2时,MCAR、TCAR和BDS/GPS三种模式NL模糊度固定成功率均达到100%,ratio阈值为3时,三种模式NL模糊度固定率依次为100%,99.98%和97.26%.ratio阈值为5时,三种模式NL模糊度固定率依次为96.58%,96.84%和64.20%,可以看出,与BDS/GPS模型直接解算NL模糊度相比,MCAR和TCAR模型NL模糊度固定的ratio值更理想。表4所示中,对于数据集C,基线长度达17km,ratio阈值为2时,MCAR、TCAR和BDS/GPS三种模式NL模糊度固定成功率达到99.68%、97.49%和96.08%,ratio阈值为3时,固定率依次为90.66%,91.048%和70.60%.ratio阈值为5时,固定率依次为39.95%,69.99%和23.39%.可以看出,即使对于长度为17km的基线,忽略电离层残差的影响,当ratio阈值为3时,MCAR和TCAR模糊度固定成功率依然高于90%,远优于BDS/GPS模型。当严格执行ratio阈值为2时,由于MCAR模型兼具TCAR算法与多系统组合的优点,因此其模糊度固定成功率是最高的。对于17km长的基线,双差电离层延迟残差使得BDS/GPS组合直接固定NL模糊度变得困难,对于MCAR和TCAR模式,通过不断精化伪距观测量,对EWL、WL和NL模糊度依次逐级固定,可保持较高的NL固定率,优于BDS/GPS模式。

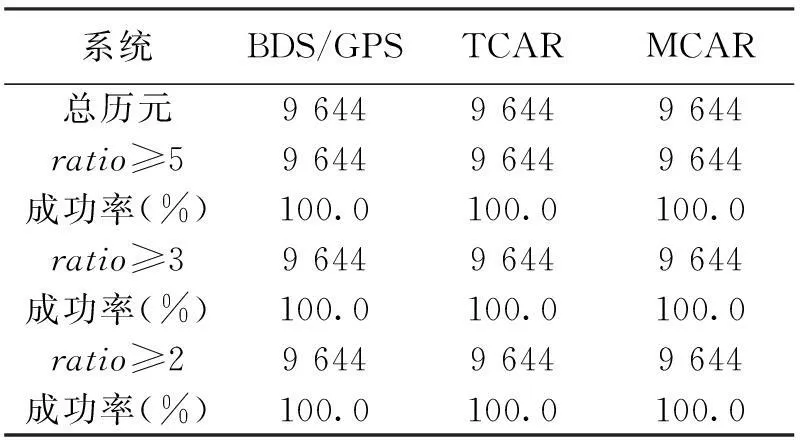
表2　模糊度解算效率比较(数据集A)

表3　模糊度解算效率比较(数据集B)

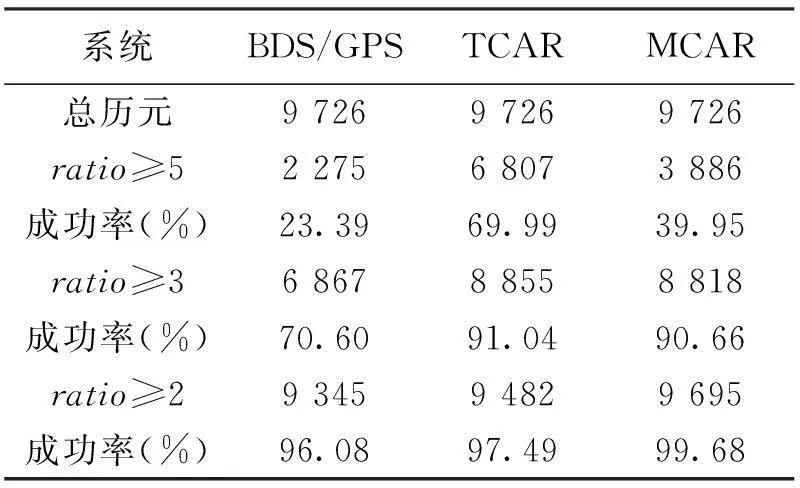
表4　模糊度解算效率比较(数据集C)

对比MCAR和TCAR两模式NL模糊度固定成功率,ratio阈值为2和3时,前者优于后者,而当ratio阈值为5时,前者略低于后者,其原因是在WL模糊度解算过程中MCAR模型引入了GPS原始伪距观测量,一定程度上抵消了模糊度已固定的EWL作为高精度伪距观测量时给WL模糊度解算带来的优势。通常情况下,对于静态基线数据,NL模糊度固定时ratio阈值不会达到5,这里采用阈值5是为了分析ratio值的分布情况,结果说明前者ratio值分布更集中,波动更小,体现出MCAR模式的稳定性要优于TCAR模式。

ratio阈值为2时,对未得到NL固定解的历元,当其浮点解与参考位置在东向和北向上的偏差小于0.1 m,在天顶向的偏差小于0.2 m时,认为其模糊度固定解被错误的拒绝了而未被采纳。对数据集进行统计得到表5～表7所示的结果。

ratio阈值为2时,由表5和表6所示可知,对于数据集A和B,三种模式下模糊度固定的错误拒绝率均为0,即没有出现解算正确却未得到固定解的情况。在表7所示中,对于数据集C,三种模式下未得到固定解但解算正确的历元数依次为352、239、31.MCAR模型的错误拒绝率仅为0.32%,远远低于BDS/GPS模型和TCAR模型,这是因为对于17 km的基线,双差电离层延迟残差使得BDS/GPS模式NL模糊度固定效率降低,而TCAR模式虽然能在一定程度上弥补了这一缺陷,但相较于MCAR模式,由于单系统条件在观测量数量、星座几何结构强度等方面要逊于双系统组合,使得解算结果不如后者。因此,MCAR模型模糊度解算的可靠性更高,效果更优。

表5　ratio阈值=2(数据集A)

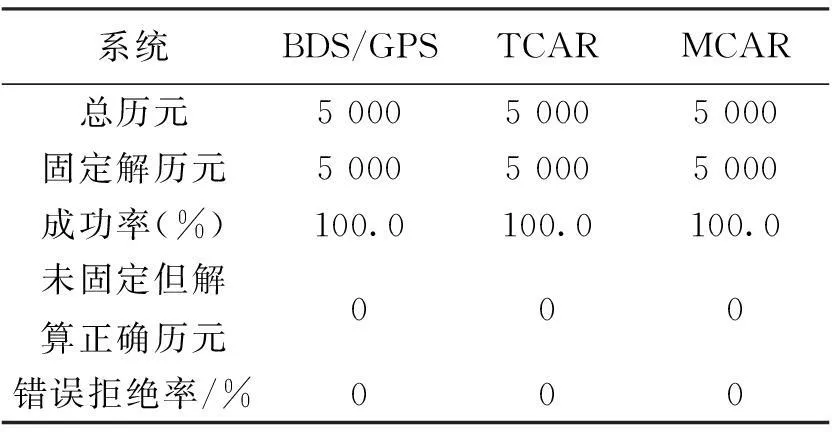
表6　ratio阈值=2(数据集B)

表7　ratio阈值=2(数据集C)

ratio阈值为2时,针对所有得到固定解的历元,将其解算得到的位置参数与参考位置作差,得到其在东、北、天三个方向的偏差,如图1～图9所示。

图1　东向定位误差时序图(数据集A)

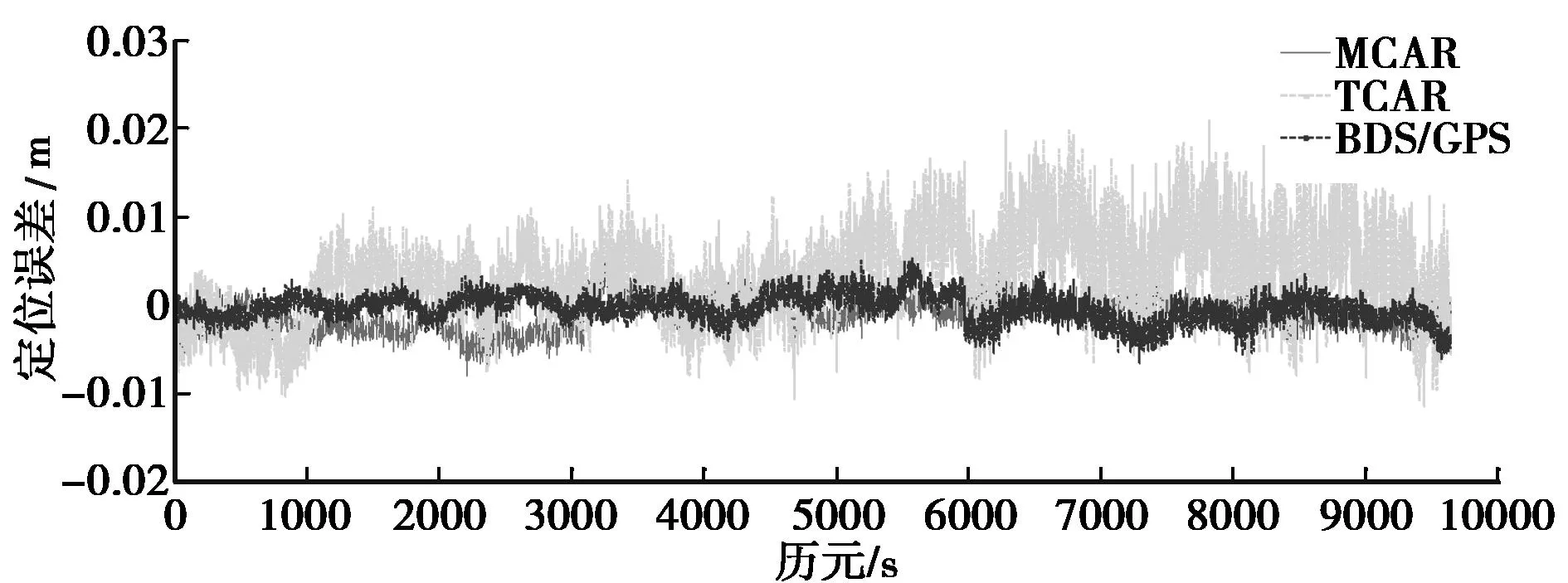
图2　北向定位误差时序图(数据集A)

图3　天顶向定位误差时序图(数据集A)

图4　东向定位误差时序图(数据集B)

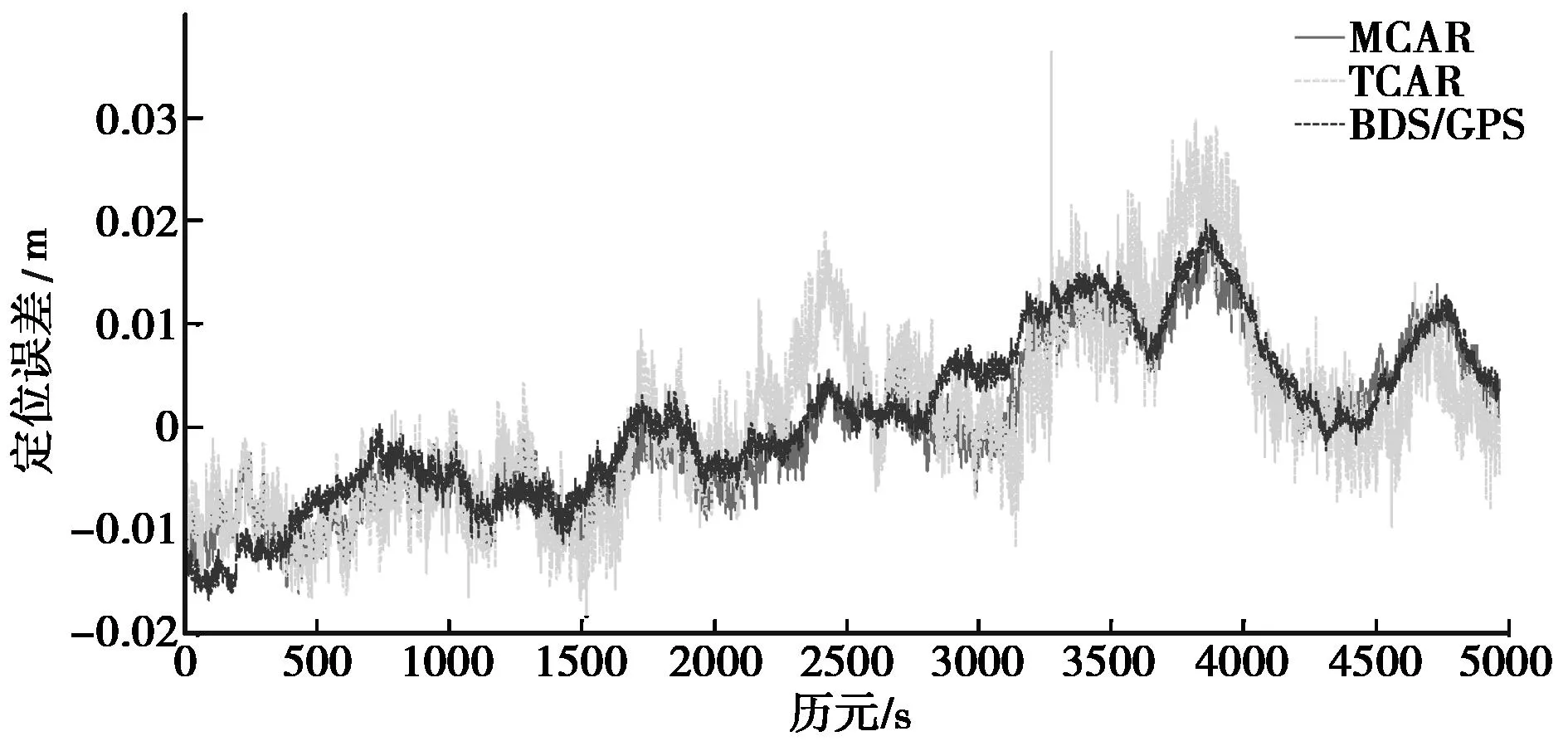
图5　北向定位误差时序图(数据集B)

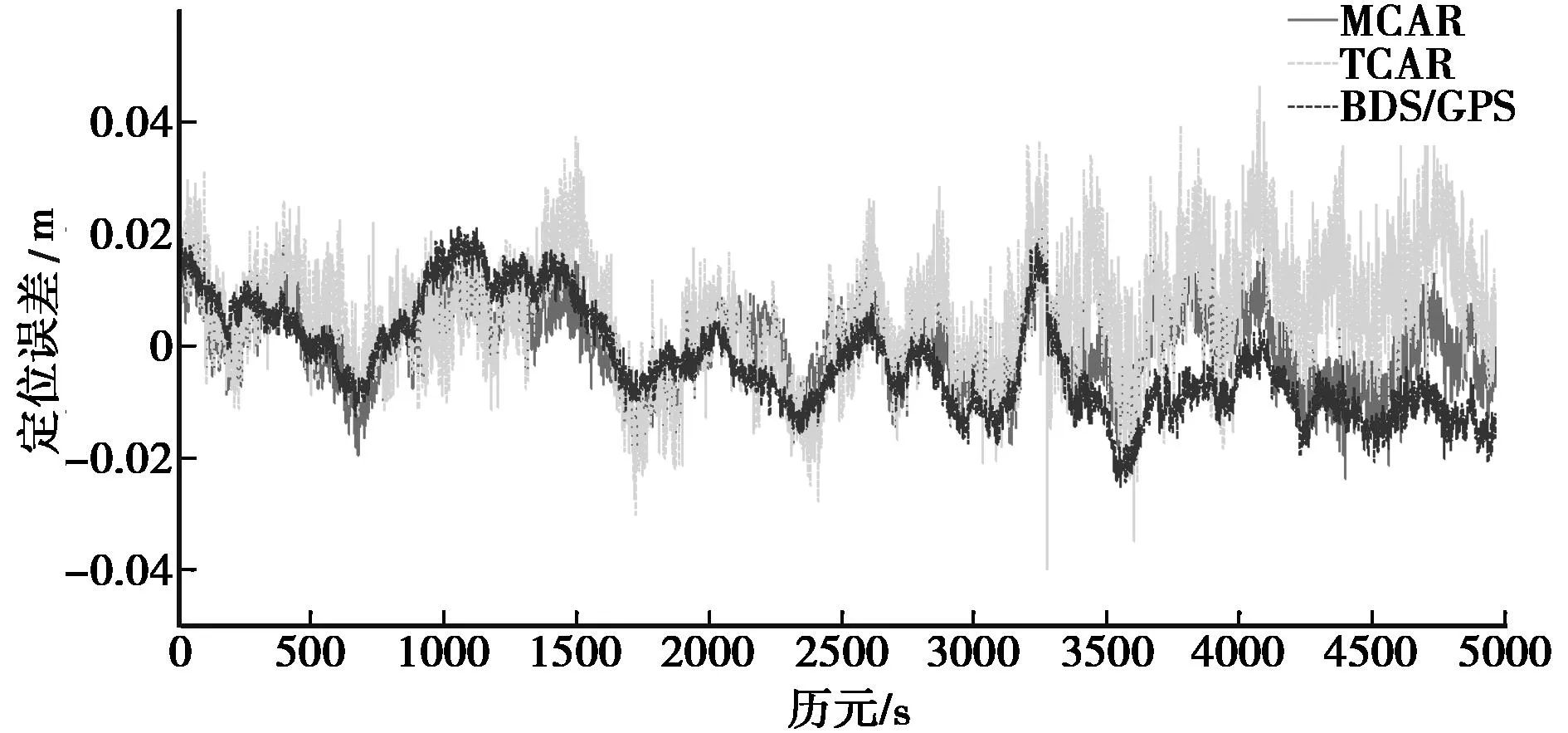
图6　天顶向定位误差时序图(数据集B)

图7　东向定位误差时序图(数据集C)

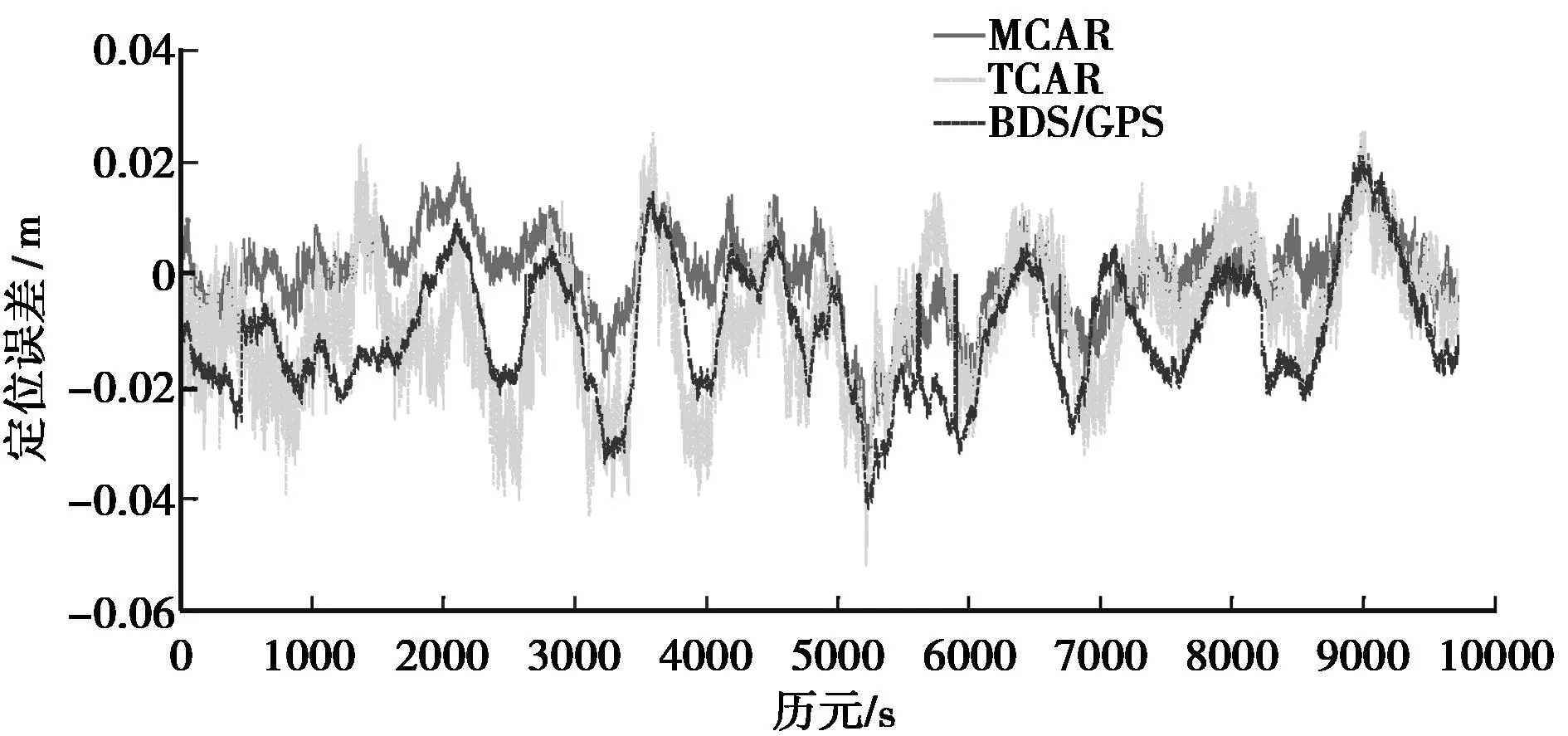
图8　北向定位误差时序图(数据集C)

图9　天顶向定位误差时序图(数据集C)

由图1～图6可以看出，对于8 m和8 km长基线，基于BDS单系统的TCAR模型在各个方向上的定位偏差波动最大，尤其在北向和天顶向最明显，说明其稳定性不如基于多系统组合的BDS/GPS模型和MCAR模型。图7、图8和图9所示中，对于数据集C，随着基线长度达到17 km，双差电离层延迟残差增大，忽略其影响时，这部分误差会被位置参数吸收，造成BDS/GPS模型定位偏差波动较大，稳定性变差，而TCAR和MCAR模式由于采用了模糊度得到固定的WL观测量，模型结构更优，一定程度上削弱了这一影响。由图8所示，TCAR模型北向上定位偏差波动较大，甚至大于BDS/GPS模型，这是由BDS星座设计的特殊性造成的，该结果与文献[7]中的结论相吻合。因此，综合来看，MCAR模型相较于其他两种模型，其定位偏差波动最小，稳定性最好。对所有得到固定解的历元在不同方向上的定位偏差进行数理统计，如表8所示。

由表8所示可以看出，对于数据集A和B，MCAR模型在各方向上的定位RMS是最小的，效果最优。对于数据集C，东向上TCAR和MCAR模型定位RMS相近，分别为0.73 cm和0.82 cm，优于BDS/GPS模型。北向和天顶方向上，MCAR模型定位RMS分别为0.8 cm和1.94 cm，均优于TCAR和BDS/GPS模型。因此，总的来看，MCAR模型定位效果优于其它两种模型。

表8　定位精度统计结果

5结束语

BDS/GPS组合定位的优点主要是可观测卫星的数量更多,观测卫星的几何图形强度更强,多余观测量更多,使得整个卫星定位系统的可靠性和可用性得到提高,尤其是对于单一卫星数量比较少或遮挡比较严重的情况,同时也提高了卫星定位系统的定位精度。基于多频观测的TCAR算法通过对原始载波相位观测量进行线性组合,可得到长波长、弱电离层延迟、弱观测噪声的最优虚拟观测量,依据波长从长到短,依次固定EWL、WL和NL模糊度,可明显提高模糊度解算效率,用于短基线单历元RTK定位时,可靠性和精度都能得到保证。

本文充分借鉴多系统组合定位和TCAR模型的优点,提出了基于双系统组合的MCAR算法,结合实测数据,就模糊度解算效率和定位精度两个指标进行了验证分析,并与其它两种模型进行了比较,结果表明本文提出的MCAR模型是最优的。

参考文献

[1] 胡自全，何秀凤，刘志平，等.GPS/GLONASS/GALILEO组合导航DOP值及可用性分析[J].全球定位系统,2012,37(5):33-39.

[2] HE H, LI J,YANG Y,etal. Performance assessment of single- and dual-frequency BeiDou/GPS single-epoch kinematic positioning[J]. GPS Solution, 2013,12(4): 131-137.

[3] DENG Chenlong ,TANG Weiming,LIU Jingnan,etal. Reliable single-epoch ambiguity resolution for short baselines using combined GPS/BeiDou system[J].GPS Solution, 2013, 17(2): 126-132.

[4] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报，2010，39(1): 1-6.

[5] 杨元喜，李金龙，徐君毅，等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报，2011，56(21)：1734-1740.

[6] 高星伟，过静琚，程鹏飞，等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报，2012,41(5)：744-75.

[7] TEUNISSEN P J G, ODOLINSKI R , ODIJK D. Instantaneous BeiDou+GPS RTK positioning with high cut-off elevation angles[J].Journal of Geodesy, 2014 (88):335-350.

[8] 李金龙. 北斗/GPS多频实时精密定位理论与算法[D].郑州：信息工程大学,2014:119-164.

[9] 李博峰.沈云中.周泽波.中长基线三频GNSS模糊度的快速算法[J].测绘学报,2009,38(4):296-301.

[10]范建军，王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报，2007，36(1)：43-49.

[11]申俊飞,何海波,郭海荣，等．三频观测量线性组合在北斗导航中的应用[J].全球定位系统,2012,37 (6): 37-40．

[12]GUO Hairong, LI Jinlong, XU Junyi,etal. Performance of triple-frequency high-precision RTK positioning with compass[C].//China Satellite Navigation Conference (CSNC) 2013 Proceedings, Lecture Notes in Electrical Engineering 243,2013.

[13]TANG Weiming, DENG Chenlong, SHI Chuang,etal. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J].GPS Solution， 2014,18(3): 335-344.

[14]李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模融合导航定位时空统一[J].大地测量与地球动力学，2013,33(4)：73-78.

[15]TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS ambiguity estimation[J]. Journal of Geodesy,1995,70(1): 65-82.

[16]CHANG X W, YANG X, ZHOU T. MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy,2005,79(9): 552-565.

[17]VOLLATH U, BIRNBACH S, LANDAU H,etal. Analysis of Three-carrier Ambiguity Resolution (TCAR) technique for precise relative positioning in GNSS-2[C].//Proceedings of ION GPS-98 The 11th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, Tennessee, USA, 1998: 417-426.

[18]JI S, CHEN W, ZHAO C,etal. Single epoch ambiguity resolution for Galileo with the CARand LAMBDA methods[J]. GPS Solution, 2007(11): 259-268.

谢建涛(1987-),男,山东潍坊人,博士生,主要从事GNSS多系统多频实时精密定位理论与算法研究。

郝金明(1962-)，男，山东曹县人，教授，博士生导师 ，主要从事卫星导航与精密定位等方面的研究。

于合理(1989-)，男，河南郸城人，博士生 ，主要从事GNSS时频传递及时差监测算法方面的研究。

田英国(1987-)，男，内蒙古乌兰察布人，博士生，主要从事星载GNSS低轨卫星精密定轨方面的研究。

张宇(1992-),男，陕西富平人，主要从事精密定位，大气影响等方面的研究。

Research of SingleEpoch and MultiFrequency BDS/GPS RTK Positioning for Short Baseline

XIE Jiantao,HAO Jinming,YU Heli,TIAN Yingguo,ZHANG Yu

(InstituteofNavigationandSpaceTargetEngineering,InformationEngineeringUniversity,Zhengzhou450052,China)

Abstract:With the number of visible satellites in the age of multiple systems for global navigation satellite system (GNSS) increasing and Chinese BeiDou satellite navigation system (BDS) beginning to offer triple frequencies signals to users, ambiguity resolution was beneficially effected, and it greatly improved the accuracy and reliability of GNSS-RTK positioning.In this paper, based on the geometric TCAR (Three Carrier Ambiguity Resolution) algorithm BDS/GPS mode was brought into the calculation of wide lane and narrow lane, then the single epoch and multifrequency BDS/GPS RTK positioning model was present. The mathematical model and its feasibility were verified by experimental data and the results showed that compared with other models, the proposed model were optimal in ambiguity resolution efficiency and positioning accuracy.

Keywords:BDS/GPS; TCAR; RTK of multi-systems; ambiguity resolution

作者简介

中图分类号：P207

文献标志码：A

文章编号：1008-9268(2016)01-0006-08

收稿日期：2015-07-15

doi:10.13442/j.gnss.1008-9268.2016.01.002

联系人： 谢建涛 E-mail: xiejiantao0911@sina.com采用TCAR算法，对BDS单历元RTK定位的性能进行了研究，结果表明即使对于长度为43 km的静态基线，模糊度解算的成功率依然能够达到94%.