大尺寸超弹性镍钛形状记忆合金螺旋弹簧滞回性能

庄鹏　聂攀　薛素铎　韩淼

摘要：利用2种镍钛形状记忆合金（SMA）研制了大尺寸超弹性螺旋弹簧，对其进行了单轴反复荷载作用下的滞回性能试验，研究了超弹性SMA螺旋弹簧的恢复力特性与耗能能力，分析了加载频率、位移幅值对2种SMA螺旋弹簧滞回曲线以及等效刚度、单位循环耗能、等效阻尼比和残余位移等力学性能参数的影响；采用刚弹性模型和BoucWen模型，建立了适用于整体结构分析的SMA螺旋弹簧简化恢复力模型，并利用该模型进行了数值模拟。结果表明：超弹性SMA螺旋弹簧具有稳定的滞回曲线，且具有良好的复位性能和大变形能力，可用于结构自复位控制装置的研发；数值模拟结果与试验结果吻合较好，验证了简化恢复力模型的正确性。

关键词：形状记忆合金；螺旋弹簧；超弹性；力学试验；滞回性能

中图分类号：TU352.1文献标志码：A

Abstract： The large scale superelastic helical springs were fabricated with two types of NiTi shape memory alloy （SMA）， and hysteretic performance test of superelastic SMA helical springs was carried out under uniaxial cyclic loading.The restoring force behavior and energy dissipation capacity of SMA helical springs were studied， and the influences of loading frequency， displacement amplitude on the hysteretic curves and the mechanical behavior parameters， such as equivalent stiffness， energy dissipation per cycle， equivalent damping ratio and residual displacement， were analyzed.Combining the rigidelastic model and the BoucWen model， a simplified restoring force model of SMA helical spring was established， which was available to integral structure， and numerical simulation was done with the model. The results show that SMA helical springs exhibit stable hysteresis curves， excellent recentering performance and large deformation capacity. The remarkable properties make the SMA spring an ideal subcomponent for use in recentering devices. The numerical results match closely with the experimental data， proving the validity of the proposed restoring force model of the SMA helical springs.

Key words： shape memory alloy； helical spring； superelasticity； mechanical experiment； hysteretic performance

0引言

形状记忆合金（Shape Memory Alloy，简称SMA）是一种新型功能材料，其在奥氏体相状态所具有的超弹性效应可用于工程结构的被动减振控制[1]。自20世纪90年代以来，各国学者利用SMA丝材研制了多种阻尼器和隔震支座[212]。近年来，随着材料加工技术的发展，大尺寸SMA部件逐渐被引入到结构减振控制中，并已成为结构振动控制技术的一个研究新热点。研究人员提出了多种含有SMA棒或大尺寸SMA螺旋弹簧的减振、隔震装置，并对其进行了理论分析和试验研究[1318]。

目前，有关大尺寸SMA螺旋弹簧的试验研究尚不够充分，科研人员对于SMA螺旋弹簧的力学行为在不同试验条件下的变化规律还缺乏深入的认识，如Speicher等[17]仅进行了单一加载频率下大尺寸SMA螺旋弹簧的拟静力试验。此外，以往SMA螺旋弹簧的数值模拟主要采用精细化有限元模型[18]，而缺少适合整体结构分析的理论模型。为了系统研究大尺寸SMA螺旋弹簧的滞回行为及其建模理论，本文选取了2种中国产镍钛形状记忆合金（NiTi SMA），研制了簧杆直径为12 mm的SMA螺旋弹簧，进行了多种工况下的单轴拉压循环力学试验，分析了加载频率、位移幅值对SMA螺旋弹簧滞回性能的影响。在此基础上建立了SMA螺旋弹簧的恢复力简化计算模型，并对恢复力模型的正确性进行了验证。本文的研究可为大尺寸SMA螺旋弹簧阻尼器的设计与性能分析提供参考。

1试验概况

1.1SMA螺旋弹簧试件

SMA螺旋弹簧分别由2种NiTi记忆合金材料制作而成，其中，材料A的化学成分为Ni50.8，Ti49.2（下标数值表示原子比百分数，单位为%），材料B的化学成分为Ni51.0，Ti49.0。材料A和材料B的奥氏体相变结束温度分别为-12.3 ℃和-26.0 ℃，故在室温下2种SMA的初始状态均为奥氏体状态。

利用上述2种SMA制作螺旋弹簧试件，分别命名为弹簧A（材料A）和弹簧B（材料B）。2种弹簧具有相同的尺寸，如图1所示。

由图5可见：弹簧A和弹簧B在正向加载和反向加载过程中均可提供光滑的梭形恢复力位移曲线，且二者的滞回曲线在正向加载和反向加载阶段基本对称，同时，2种弹簧在卸载后几乎无残余变形；当位移幅值由12 mm增至36 mm时，弹簧A的滞回曲线加载段未出现非线性强化；当位移幅值小于20 mm时，弹簧B的加载段曲线未出现非线性强化，但是当位移幅值区间为28～36 mm时，弹簧B的加载段曲线斜率增加，使得其滞回曲线出现硬化的趋势。

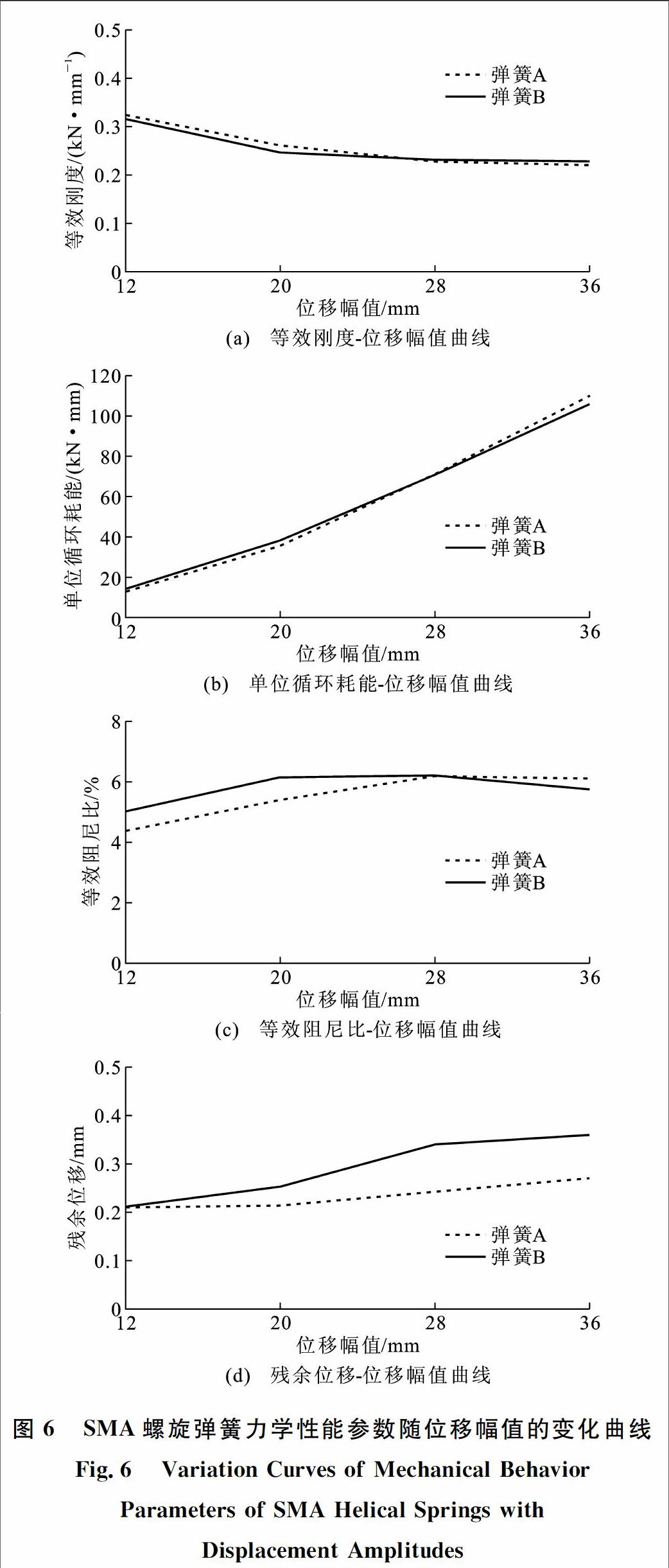
由图6可见：2种弹簧的等效刚度随位移幅值的增加而降低，如弹簧A的等效刚度由位移幅值为12 mm时的0.323 1 kN·mm-1降至位移幅值为36mm时的0.219 4 kN·mm-1，减小29.0%，相同条件下弹簧B的等效刚度由0.314 9 kN·mm-1降至0.226 8 kN·mm-1，减小28.29%；2种弹簧的单位循环耗能随着位移幅值的增加而增大，当位移幅值由12 mm增至36 mm时，弹簧A的单位循环耗能由12.781 3 kN·mm增至110.342 9 kN·mm，增加了763.32%，弹簧B的单位循环耗能由14.271 9 kN·mm增至106.103 9 kN·mm，增加了643.45%；2种弹簧的等效阻尼比均随位移幅值的增加而增大，在位移幅值为28 mm时达到最大，在这一位移幅值下弹簧A和弹簧B的等效阻尼比分别为6.18%和6.22%，其后继续增大位移幅值，2种弹簧的等效阻尼比略微降低，位移幅值为36 mm时弹簧A和弹簧B的等效阻尼比分别为6.12%和5.75%；2种弹簧的残余位移随位移幅值的增加而增大，位移幅值为36 mm时，弹簧A和弹簧B的残余位移分别为0.27 mm和0.36 mm，其值较位移幅值为12 mm时2种弹簧的残余位移分别增加了35.0%和71.43%，在整个位移幅值区间内，弹簧A的残余位移占位移幅值的0.75%～1.67%，弹簧B残余位移占位移幅值的1.0%～1.75%，2种SMA螺旋弹簧的残余位移均极小。

3SMA螺旋弹簧恢复力的数值模拟

3.1简化计算模型

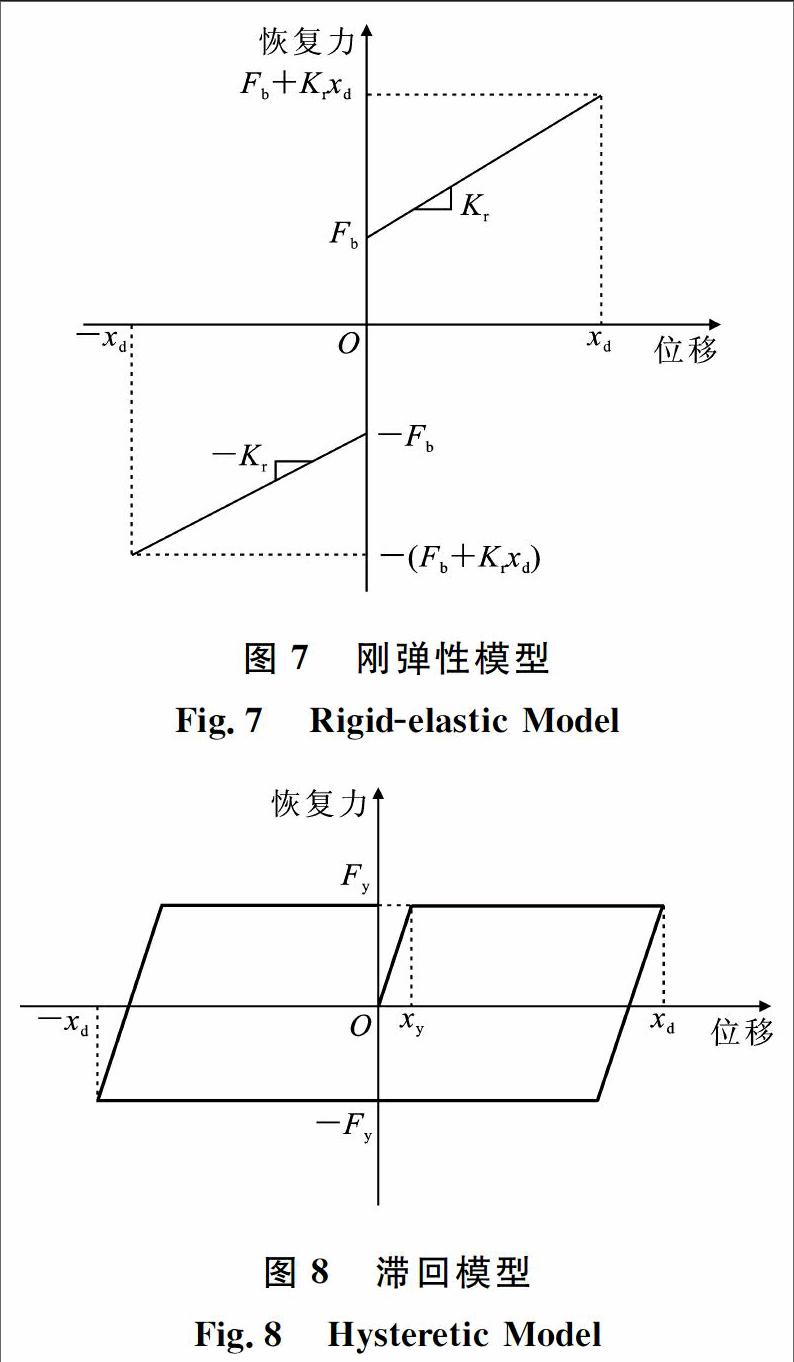
现有关于SMA减振装置的数值模拟主要采用分段线性模型，但是通过分段线性模型得到的恢复力位移曲线在转折处带有尖角，将其用于受控结构动力分析可能导致计算结果失真。基于实体单元的精细化有限元模型也可用于SMA螺旋弹簧的数值模拟，但其计算效率较低，难以用于整体结构的分析。为了便捷地模拟出光滑的恢复力位移曲线，本文选择适当的函数建立SMA螺旋弹簧简化滞回模型，并利用试验结果对模型的正确性进行验证。

3.2模拟结果与分析

以不同位移幅值下2种SMA螺旋弹簧滞回行为的数值模拟为例考察本文恢复力模型的正确性。首先，通过不同位移幅值下的试验数据确定弹簧A和弹簧B的屈服位移xy取值分别为4.6 mm和4.5 mm，屈服后刚度分别为0.1914 kN·mm-1和0.199 8 kN·mm-1。进而，利用不同位移幅值下的试验结果可确定最大恢复力Fd的取值（表1）。在此基础上，通过求解式（7）得到不同位移幅值下的恢复力模型特征参数取值，其中，当弹簧A的位移幅值分别为12，20，28，36 mm时，对应的Fb分别为0.753 3，0.755 3，0.733 8，0.743 0 kN，而相同位移幅值下Fy的取值与Fb的取值相同；同理，在上述位移幅值下，弹簧B的Fb等于Fy，对应于12，20，28，36 mm四种位移幅值的Fb分别为0.565 3，0.578 3，0.521 1，0.538 7 kN。此外，BoucWen模型中的常数α，γ，β，A，n统一取为0，0.5，0.5，1，2。基于以上参数取值，按照式（3）～（6）编写MATLAB计算程序。表2和表3分别给出了不同位移幅值下2种SMA螺旋弹簧的等效刚度、单位循环耗能、等效阻尼比试验值与模拟值，可见力学性能参数试验值和模拟值之间的相对误差绝大部分在10%以内，仅有个别相对误差在10%～15%之间。研究结果表明，本文简化恢复力模型能够较好地模拟SMA螺旋弹簧的恢复力位移滞回曲线。

4结语

（1）随着加载频率的增加，2种SMA螺旋弹簧的恢复力位移曲线在正向加载阶段和反向加载阶段分别向斜上方和斜下方发展；在试验研究的加载频率区间内，2种SMA螺旋弹簧的等效刚度均逐渐增加，单位循环耗能和等效阻尼比则变化较小，残余位移均有所增大。

（2）随着位移幅值的增加，2种SMA螺旋弹簧的滞回环均在坐标系内渐呈狭长的梭形；在位移幅值区间内，2种弹簧的单位循环耗能均成倍增加，等效阻尼比均在位移幅值为28 mm时达到最大值，随后等效阻尼比有所减小；卸载后2种弹簧的残余位移均累积增加，但其值极小。

（3）基于刚弹性模型和BoucWen模型可建立大尺寸SMA螺旋弹簧的简化恢复力模型，使用该简化模型能够较好地描述记忆合金螺旋弹簧的滞回行为，且力学性能参数的模拟值与试验值较为接近，从而验证了该模型的合理性与有效性。

参考文献：

References：

[1]GRAESSER E，COZZARELLI F.Shape Memory Alloys as New Materials for Aseismic Isolation[J].Journal of Engineering Mechanics，1991，117（11）：25902608.

[2]DOLCE M，CARDONE D，MARNETTO R.Implementation and Testing of Passive Control Devices Based on Shape Memory Alloys[J].Earthquake Engnineering and Structural Dynamics，2000，29（7）：945968.

[3]DOLCE M，CARDONE D，PONZO F，et al.Shaking Table Tests on Reinforced Concrete Frames Without and with Passive Control Systems[J].Earthquake Engnineering and Structural Dynamics，2005，34（14）：16871717.

[4]OZBULUT O，HURLEBAUS S.Optimal Design of Superelasticfriction Base Isolators for Seismic Protection of Highway Bridges Against Nearfield Earthquakes[J].Earthquake Engineering and Structural Dynamics，2011，40（3）：273291.

[5]李忠献，陈海泉，刘建涛.应用SMA复合橡胶支座的桥梁隔震[J].地震工程与工程振动，2002，22（2）：143148.

LI Zhongxian，CHEN Haiquan，LIU Jiantao.Bridge Isolation with SMAcomposite Rubber Bearing[J].Earthquake Engineering and Engineering Vibration，2002，22（2）：143148.

[6]李惠，毛晨曦.新型SMA耗能器及结构地震反应控制试验研究[J].地震工程与工程振动，2003，23（1）：133139.

LI Hui，MAO Chenxi.Experimental Investigation of Earthquake Response Reduction of Buildings with Added Two Types of SMA Passive Energy Dissipation Devices[J].Earthquake Engineering and Engineering Vibration，2003，23（1）：133139.

[7]薛素铎，董军辉，卞晓芳，等.一种新型形状记忆合金阻尼器[J].建筑结构学报，2005，26（3）：4550.

XUE Suduo，DONG Junhui，BIAN Xiaofang，et al.A New Type of Shape Memory Alloy Damper[J].Journal of Building Structures，2005，26（3）：4550.

[8]赵祥，王社良，周福霖，等.基于SMA阻尼器的古塔模型结构振动台试验研究[J].振动与冲击，2011，30（11）：219223.

ZHAO Xiang，WANG Sheliang，ZHOU Fulin，et al.Shaking Table Tests for Ancient Pagoda Model Structure Based on Shape Memory Alloy Actuating Devices[J]. Journal of Vibration and Shock，2011，30（11）：219223.

[9]钱辉，李宏男，任文杰，等.形状记忆合金复合摩擦阻尼器设计及试验研究[J].建筑结构学报，2011，32（9）：5864.

QIAN Hui，LI Hongnan，REN Wenjie，et al.Experimental Investigation of an Innovative Hybrid Shape Memory Alloys Friction Damper[J].Journal of Building Structures，2011，32（9）：5864.

[10]任文杰，李宏男，宋钢兵，等.新型自复位SMA阻尼器对框架结构减震控制的研究[J].土木工程学报，2013，46（6）：1420.

REN Wenjie，LI Hongnan，SONG Gangbing，et al.Study on Seismic Response Control of Frame Structure Using Innovative Recentering SMA Damper[J].China Civil Engineering Journal，2013，46（6）：1420.

[11]ATTANASI G，AURICCHIO F，URBANO M.Theoretical and Experimental Investigation on SMA Superelastic Springs[J].Journal of Materials Engineering and Performance，2011，20（4）：706711.

[12]黄斌，蒲武川，张海洋，等.基于超弹性SMA螺旋弹簧的基础隔震研究[J].地震工程与工程振动，2014，34（2）：209215.

HUANG Bin，PU Wuchuan，ZHANG Haiyang，et al.Study on Seismic Responses of Base Isolated Structures with Superelastic SMA Helical Springs[J].Earthquake Engineering and Engineering Vibration，2014，34（2）：209215.

[13]MILLER D，FAHNESTOCK L，EATHERTON M.Development and Experimental Validation of a Nickeltitanium Shape Memory Alloy Selfcentering Bucklingrestrained Brace[J].Engineering Structures，2012，40：288298.

[14]BHUIYAN A，ALAM M.Seismic Vulnerability Assessment of a Multispan Continuous Highway Bridge Fitted with Shape Memory Alloy Bars and Laminated Rubber Bearing[J].Earthquake Spectra，2012，28（4）：13791404.

[15]陈鑫，李爱群，丁幼亮，等.空间网架结构形状记忆合金隔震研究[J].工程力学，2010，27（9）：8693，101.

CHEN Xin，LI Aiqun，DING Youliang，et al.Study on Isolation of Space Grid Structure Using Shape Memory Alloy[J].Engineering Mechanics，2010，27（9）：8693，101.

[16]何小辉.钢框架新型耗能梁柱节点滞回性能的研究[D].哈尔滨：哈尔滨工业大学，2012.

HE Xiaohui.Hysteretic Behavior of New Energydissipated Beamtocolumn Connections in Steel Frame[D].Harbin：Harbin Institute of Technology，2012.

[17]SPEICHER M，HODGON D，DESROCHES R，et al.Shape Memory Alloy Tension/Compression Device for Seismic Retrofit of Buildings[J].Journal of Material Engineering and Performance，2009，18（5）：746753.

[18]MIRZAEIFAR R，DESROCHES R，YAVARI A.A Combined Analytical，Numerical and Experimental Study of Shapememoryalloy Helical Springs[J].International Journal of Solids and Structures，2011，48（3/4）：611624.

[19]WEN Y K.Method for Random Vibration of Hysteretic System[J].Journal of the Engineering Mechanics Division，1976，102（2）：249263.