开口肋加劲板屈曲模态与临界屈曲应力分析

赵秋　翟战胜

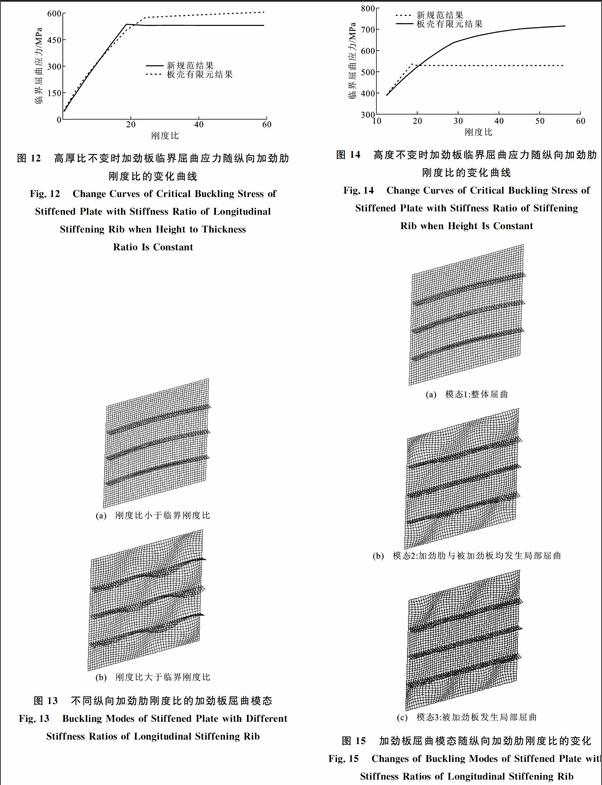
摘要：为更好掌握开口肋加劲板的设计计算方法，采用弹性稳定分析方法，对无纵向和横向加劲肋的四边简支板、纵向加劲肋等间距布置的四边简支加劲板、纵向和横向加劲肋等间距布置的加劲板进行屈曲模态和临界屈曲应力分析。结果表明：对于四边简支板或四边简支加劲板，临界屈曲应力与板宽、板长和板厚均有关，减小板宽和板长以及增大板厚可提高临界屈曲应力；随着加劲肋刚度比的变化，四边简支加劲板一般表现出3种屈曲模态，模态1为加劲肋与被加劲板共同发生整体屈曲，模态2为在加劲肋处形成波节，加劲肋与被加劲板发生屈曲，模态3为加劲肋为刚性加劲肋，不会发生失稳，只有被加劲板发生局部失稳；临界屈曲应力随加劲肋刚度比的增大而增大，模态1增大幅度最大，模态2次之，模态3逐步趋于定值。

关键词：开口肋加劲板；弹性稳定；屈曲模态；临界屈曲应力；加劲肋；临界刚度比

中图分类号：TU311文献标志码：A

Abstract： In order to master the design and calculation method of openrib stiffened plate better， the buckling modes and critical buckling stress of fourside simplysupported plate without longitudinal and transversestiffening ribs，fourside simplysupportedstiffened plate withlongitudinal stiffening ribs arranged by equal distance， stiffened plate with longitudinal and transverse stiffening ribs arranged by equal distance， were analyzed by elastic stabilitytheory. The results show that critical buckling stress is related to plate width， plate length and plate thickness for foursidesimplysupported plate or fourside simplysupportedstiffened plate. Critical buckling stress can be improved with the decrease of plate width and plate length， and with the increase of thickness of plate. There are 3 kinds of buckling modes of fourside simplysupported stiffened plate with changes of stiffness ratios of stiffening ribs. Stiffening ribs and stiffened plate are overall buckling in mode 1. Wave nodes are formed on stiffening ribs， stiffening ribs and stiffened plate are buckling in mode 2. Stiffening ribs will not appear instable， only stiffened plate is buckling in mode 3.Critical buckling stress increases with the increase of stiffness ratio of the stiffening rib， the increase range is maximal in mode 1， and comes second in mode 2. Critical buckling stress tends to be constant value in mode 3.

Key words： openrib stiffened plate； elastic stability； buckling mode； critical buckling stress； stiffening rib； critical stiffness ratio

0引言

对于受压加劲板来说，稳定问题和强度问题同样重要[12]。受压加劲板的弹性稳定分析在稳定问题中属于第1类稳定问题，即平衡分岔失稳问题，这是一种理想化的情况，当达到某荷载时，结构除了可能存在原来的平衡状态外，会出现第2个平衡状态，而在数学处理上是求解特征值问题，故又称为特征值屈曲分析，其目的是求解临界荷载值[35]。虽然受压加劲板弹性稳定计算比较简单，但它是稳定承载力分析的基础。当受压加劲板发生屈曲时，其变形形状经常被称为屈曲模态[610]。由于受压结构不同的屈曲模态将导致不同的稳定承载力，对于受压加劲板来说，由于组成结构各部分刚度的改变，失稳将有较多的屈曲模态[1114]。因此，本文采用理论分析和有限元分析相结合的方法对受压弹性稳定和屈曲模态进行分析，加深对即将颁布的新规范的理解，并为受压加劲板稳定承载力计算提供参考。

1理论与有限元分析方法

1.1受压板和受压加劲板稳定计算

1.2有限元模型

有限元模型采用考虑大变形的Shell181壳单元，弹性模量为2.06×105 MPa，泊松比为0.3，模型的边界条件为四边均约束Z方向的位移，其中平行于X轴的a/2处两节点约束Y方向位移（a为加劲板长度），平行于Y轴的b/2处两边中点约束X方向位移。有限元模型如图1所示。