岩巷爆破振动信号的HHT分析与应用

孙 强， 王梦晓， 徐玉山， 刘国有

(中国矿业大学(北京) 力学与建筑工程学院， 北京 100083)



岩巷爆破振动信号的HHT分析与应用

孙 强， 王梦晓， 徐玉山， 刘国有

(中国矿业大学(北京) 力学与建筑工程学院， 北京 100083)

摘要：为优化爆破参数，减少对围岩的损伤，以煤矿玄武岩双巷道楔形深孔掏槽爆破的实测爆破振动信号为例，分析对比传统傅里叶变换、小波变换、HHT变换三种变换方法，对爆破地震波信号的时频特性和能量分布特征分析。结果表明： HHT变换能够确保信号被分解后的非平稳性，且自动适应能力较强，分解效率较高。通过HHT变换得到三维图直观展示各分量随时间、频率和能量的分布情况。爆破振动能量主要分布在0.3s~1.0s时间段和0~400Hz频率段内，频带100Hz～250Hz中爆破振动分量对应的频带能量达到最大。通过分析对比爆破振动信号，得到巷道帮部、底部爆破振动信号的主振方向分别为Y(切向)和Z(垂向)方向。

关键词：岩石巷道； 爆破振动； 振动信号； HHT； 时频； 能量

1引 言

煤炭是我国不可缺少的基础性能源, 其中岩石巷道掘进是煤矿生产的重要环节，提高掘进效率是矿井安全生产满足采掘平衡的保障。在岩石巷道掘进中，爆破振动对周围环境影响是无法避免的公害〔1〕。因此基于爆破振动引起的爆破地震效应的研究就显得极为重要。针对爆破地震效应，国内外进行了大量的研究，而且取得了丰硕的成果。研究成果多集中在地面以上(露天矿山、公路、铁路)、地铁和水工隧道等方面〔2-4〕。整体来看，在煤矿井下采掘爆破振动的研究方面，主要采用萨式公式对爆破振动测试结果进行回归分析，对爆破地震波的频率与能量分布关系研究较少〔5〕。工程实践也表明〔6-7〕，若以单一质点的振动速度作为衡量爆破振动强度的唯一指标，缺少对地震波频率和振动持续时间、能量等因素影响的考虑，对于建筑物的实际破损情况在很多情况下也不能很好地反映。因此，本文针对硬度较大的岩石巷道爆破振动信号分析进行了相关的理论分析、比较和总结，选取HHT分析方法，有效提取爆破振动信号的时频特性和能量分布特征，对于岩石巷道爆破中降低爆破振动效应，减少爆破振动测试误差，指导爆破设计均具有重要意义。

2爆破振动信号分析方法

2.1不同的爆破振动信号分析方法

对爆破振动信号采用各种数字信号处理方法进行分析与处理，可以提取各种时间、频率的特征信息，对信号进行时频分析与处理，全面地提取信号主要特征信息〔8〕。基于传统傅里叶变换(FFT)理论，短时傅里叶变换(STFT)和小波变换(WT)在爆破信号处理中已作为分析信号的普适方法〔9〕。

(1)傅里叶变换处理信号仅限于局部的频域范围内进行分析，无法从时间域角度进行信号分析。STFT以傅里叶变换为主要依据，是最常用的时频分析方法〔10-11〕。STFT首先将时间窗加载到时间信号上，然后对时间窗的数据信号进行傅里叶变换，就可以从频率和时间角度得到信号的短时时频谱〔12〕，其表达式为：

(1)

式中：*为复共轭；g(t)为有紧支撑的函数；f(t)为原始数据信号。

(2)WT是分析数据信号部时频特征的新方法，其特点是保持窗口的面积不发生变化，窗口的形状可以随着分析情况的变化而逐渐变化，即时间窗口和频率窗口都可以随着分析情况的变化而变化〔13-14〕。

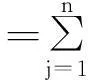
2.2不同变换的比较

三种不同变换的基本性质差异对比见表1。

表1　不同变换的基本性质

通过比较可得：三种变换方法在信号分析采用的基函数不同，基函数不同则对信号的分解也不同，进而得到差别较大的结果，无法进行统一分析。傅里叶变换采用正弦或者余弦函数作为分解的基函数；小波函数的基函数是选择预先设定的，不随波自身的参数而改变，故选择不同基函数时得出的结果差别较大，给分析带来一定的困难；而EMD分析方法则是依据数据信号本身的特性，在时域内进行自动适应性分解，没有预定函数的选择，这样分解可以得到较好的分析效果。而且，EMD分解得到的IMF分量都是平稳的，且比傅里叶变换和小波法有更强的局部特性。整体来说，HHT变换方法自动适应能力较强，分解效率较高，更适应突变、衰减快的数据信号。

3实例与分析

3.1地质条件与爆破条件

测试地点为大安山煤矿+400m西大巷，矿岩石类型主要为玄武岩(辉绿岩)，岩石致密度较高，层理节理不发育，岩石硬度较大。玄武岩坚硬普氏系数： f=8～20。因岩石硬度较大，采用分段爆破。分段爆破中掏槽孔较为重要，其好坏直接影响其他炮孔的爆破效果，所以对掏槽孔孔就行分析研究。掏槽孔爆破参数见表2。

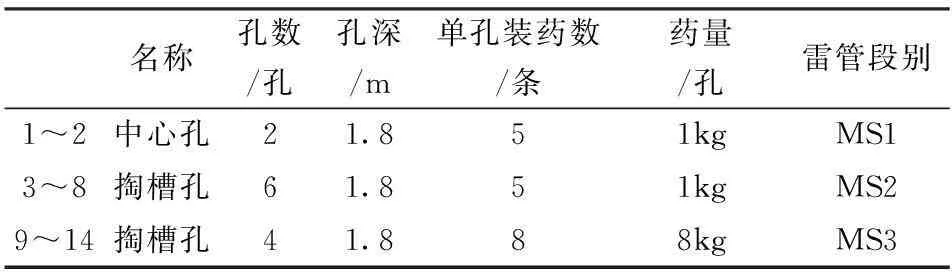
表2　掏槽孔爆破参数

3.2爆破测振仪的选择与振动监测试验方案

试验应用TC-4850爆破测振仪和Minimate Plus型爆破测振仪进行巷道爆破振动现场测试。

岩石巷道掘进爆破引起的洞内振动速度，最大值是出现在拱顶、拱腰或是拱墙，目前没有达成共识。试验时从监测的便捷性和不影响施工的角度考虑，将监测仪器放置于底板的中心线与腰线上并加以保护盒，防止岩石抛掷过远砸坏传感器，同时防止岩石碰到传感器而触发电平。监测时每个特定距离布置监测点，即放置传感器和信号接收器，传感器布置和仪器保护盒分别如图1和图2所示。

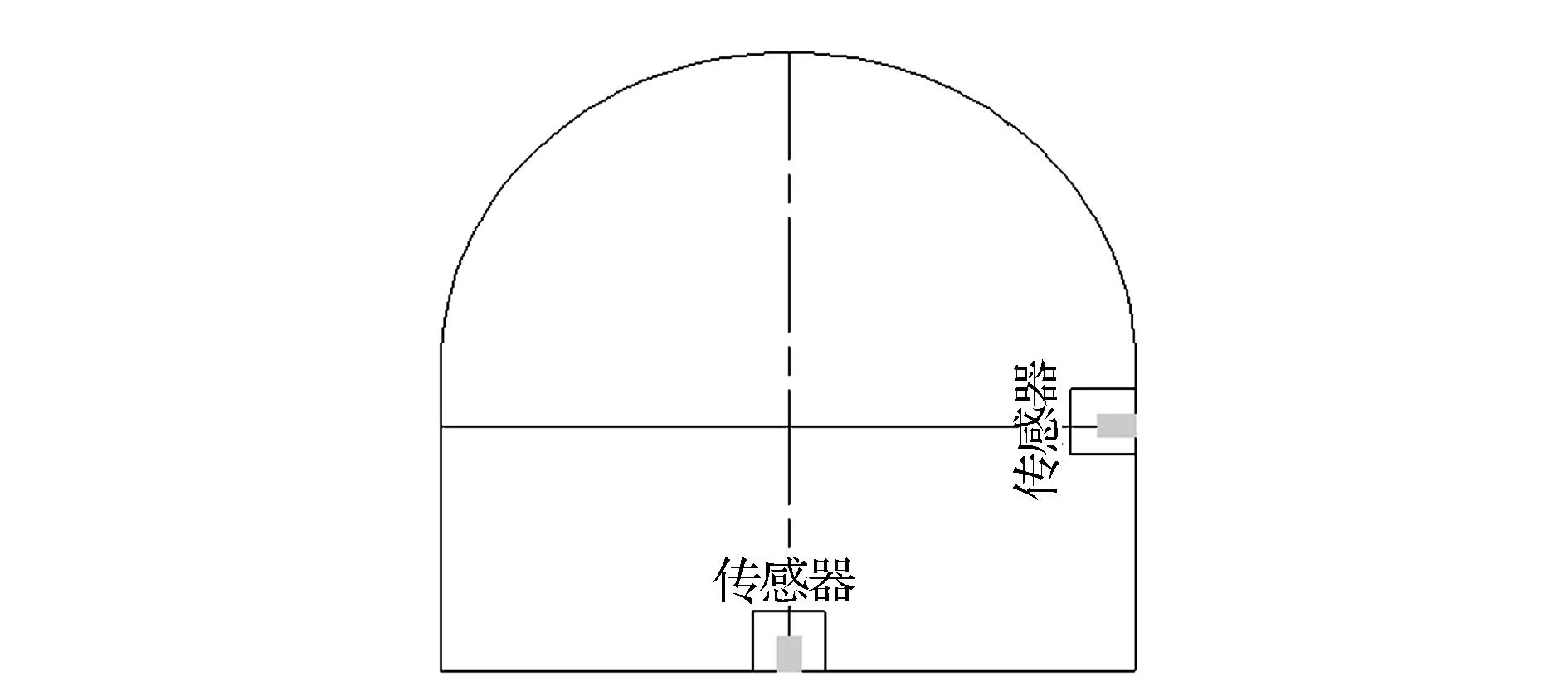
图1　现场监测点布置图Fig.1　Site monitoring point layout

图2　振动测试仪器保护盒示意图Fig.2　Vibration testing equipment protection box

3.3掏槽孔爆破振动典型波形统计

在大安山硬度较大的玄武岩巷道进行双道巷楔形深孔掏槽爆破时，现场采集信号，选取典型信号如图3~图4所示。

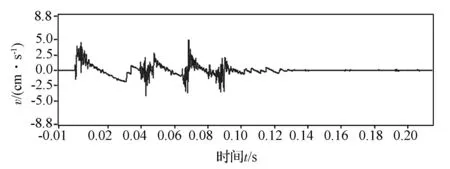
图3　帮部爆破振动信号典型波形图Fig.3　Typical waveform diagram of blasting vibration signal

图4　底部爆破振动信号典型波形图Fig.4　Typical waveform diagram of blasting vibration signal

爆破振动数据统计见表3。

表3　玄武岩巷道帮部与底部爆破振动数据

根据分析对比已测波形可得，在大安山硬度较大的玄武岩巷道进行双道巷楔形深孔掏槽爆破时，帮部与底部的振动信号分别在Y(切向)方向与Z(垂向)方向波速最大，所以其为主振方向。选取主振方向的典型波形如图3和4所示。分析得：爆破振动波形振荡时间为10ms~20ms，间隔时间为25ms左右，与雷管的延时相符合，整个波形全部振荡时间约为120ms。

3.4爆破振动信号的HHT分析

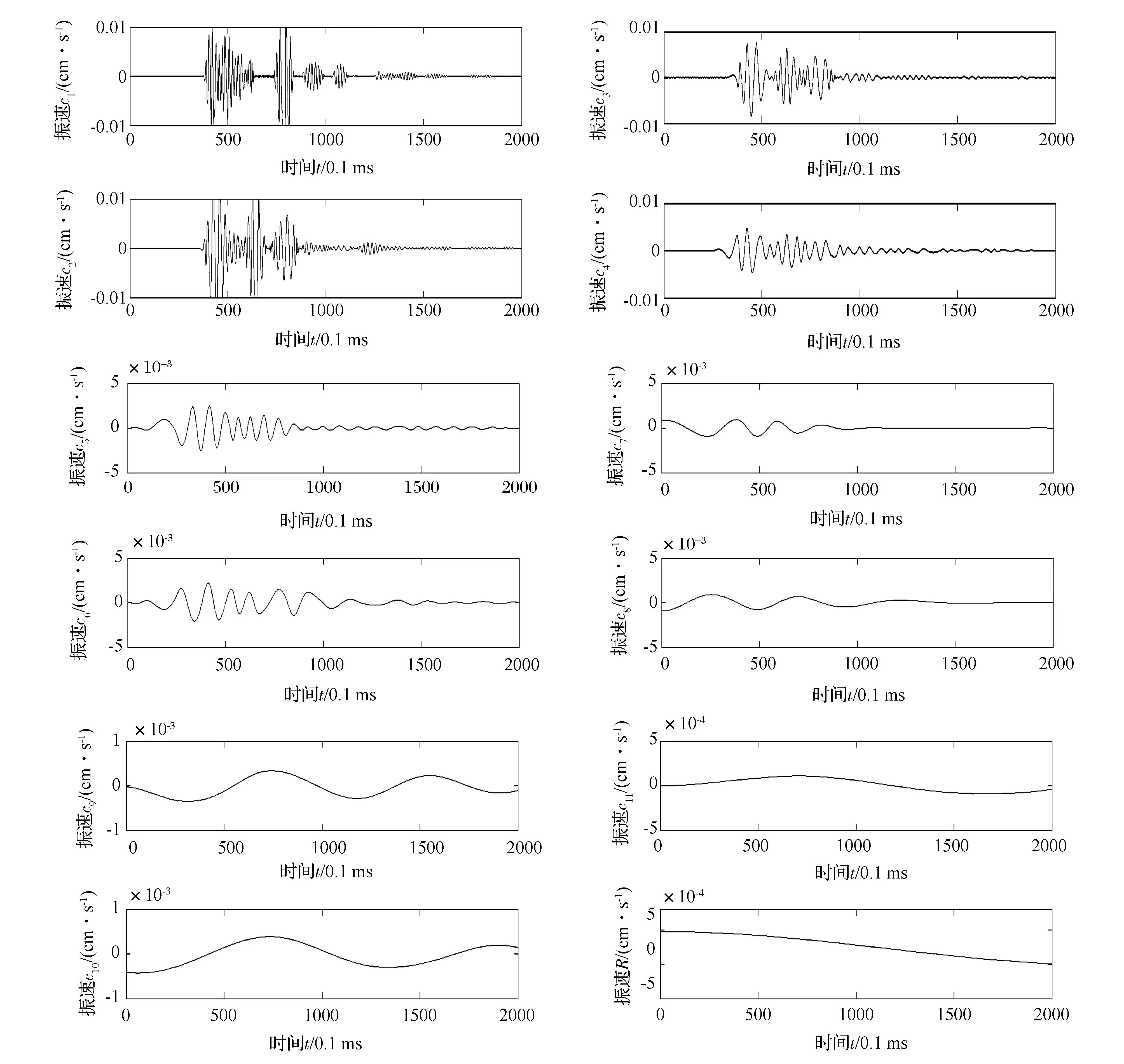
图5　爆破振动信号的EMD分解Fig.5　EMD decomposition of blasting vibration signals

应用MATLAB程序对大安山煤矿+400m水平岩石巷道掘进爆破所监测到的底部振动信号典型波形图4进行经验模态分解，得到11个IMF分量和趋势项R，如图5所示。每个IMF分量包含了不同的时间尺度，用不同的分辨率来反映信号的相关特性，说明经验模态分解中分辨率具有自动适应性。分解出的所有IMF分量中，c1~c4分量频率较高，相应的波长较短，是振动信号的主要组成部分。其中c1分量频率最高，含有的能量极小，这说明c1分量是在数据监测中引入了高频率的噪声，应该在分析过程中除去噪声。其他IMF对应的每个分量的频率依次降低、波长依次变长，直至分解得出趋势余量R。表明在爆破振动波传播过程中高频值已大大衰减，然而其幅值却有不同程度的增加。

将所有分解得到的IMF分量分别进行Hilbert变换，趋势项R不存在频率，因此只需要分析前11个IMF分量的瞬时频率，如图6所示。

图6　IMF分量的Hilbert时频谱Fig.6　IMF component of Hilbert

通过进一步计算求出Hilbert二维能量谱(图7)、Hilbert边际谱(图8)、Hilbert边际能量谱(图9)、瞬时能量谱(图10)、三维能量谱(图11)。

Hilbert二维能量谱形象反映出振动信号能量与时间和频率的分布关系，由图7得出绝大部分能量都集中在时间段0.3s~1.0s和频率0~400Hz范围内。从分辨率方面来说，基于测不准原理的因素，傅里叶谱和小波谱的分辨率大大低于Hilbert谱，并且Hilbert谱非常形象和准确的刻画出在全局范围内信号的幅值随着频率和时间的变化规律。由图8可以得出数据信号的能量与频率的关系，而且可以得出能量主要集中在300Hz以内。

图7　Hilbert二维能量谱Fig.7　Dimensional Hilbert energy spectrum

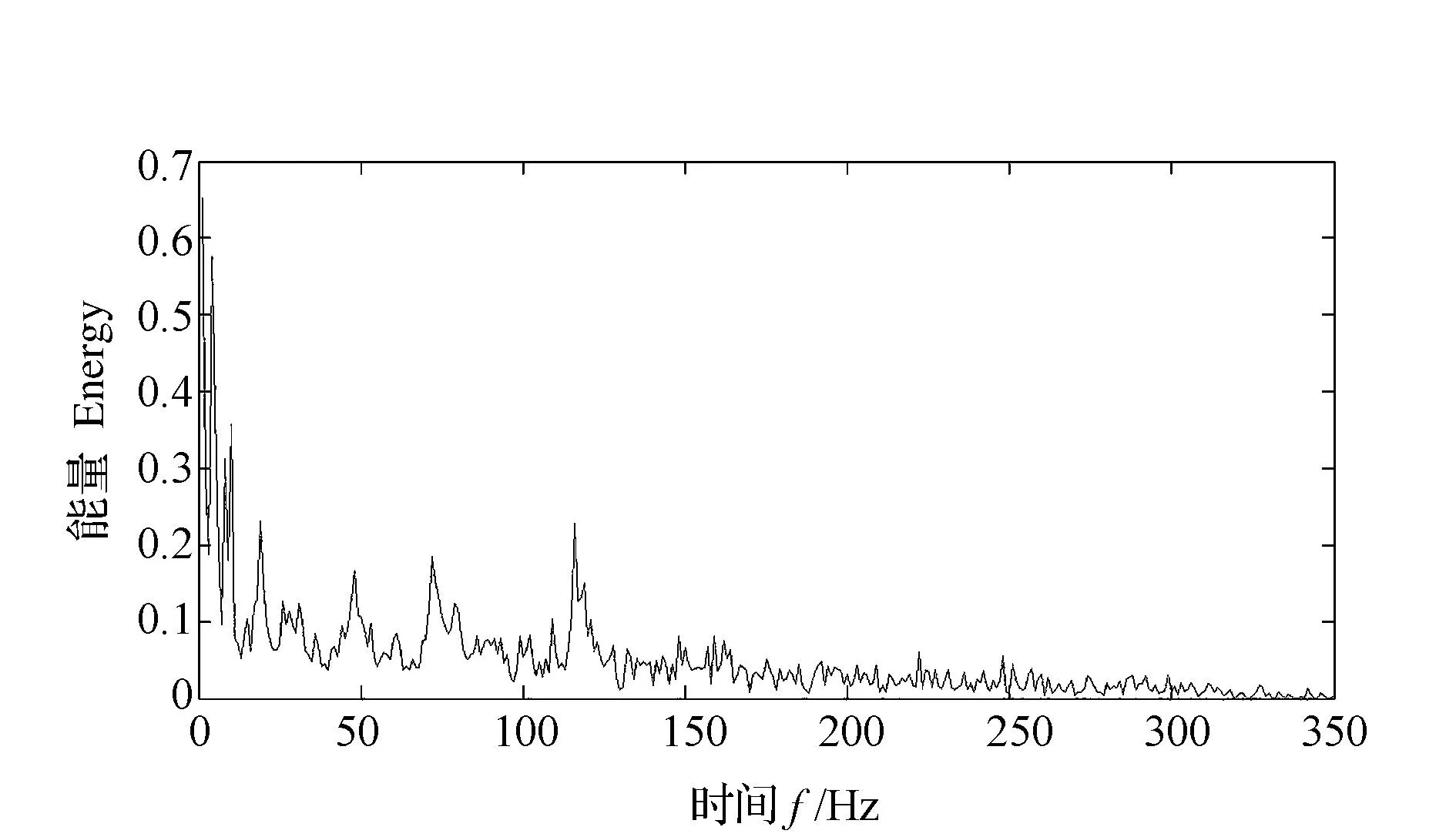
图8　Hilbert边际谱Fig.8　Hilbert marginal spectrum

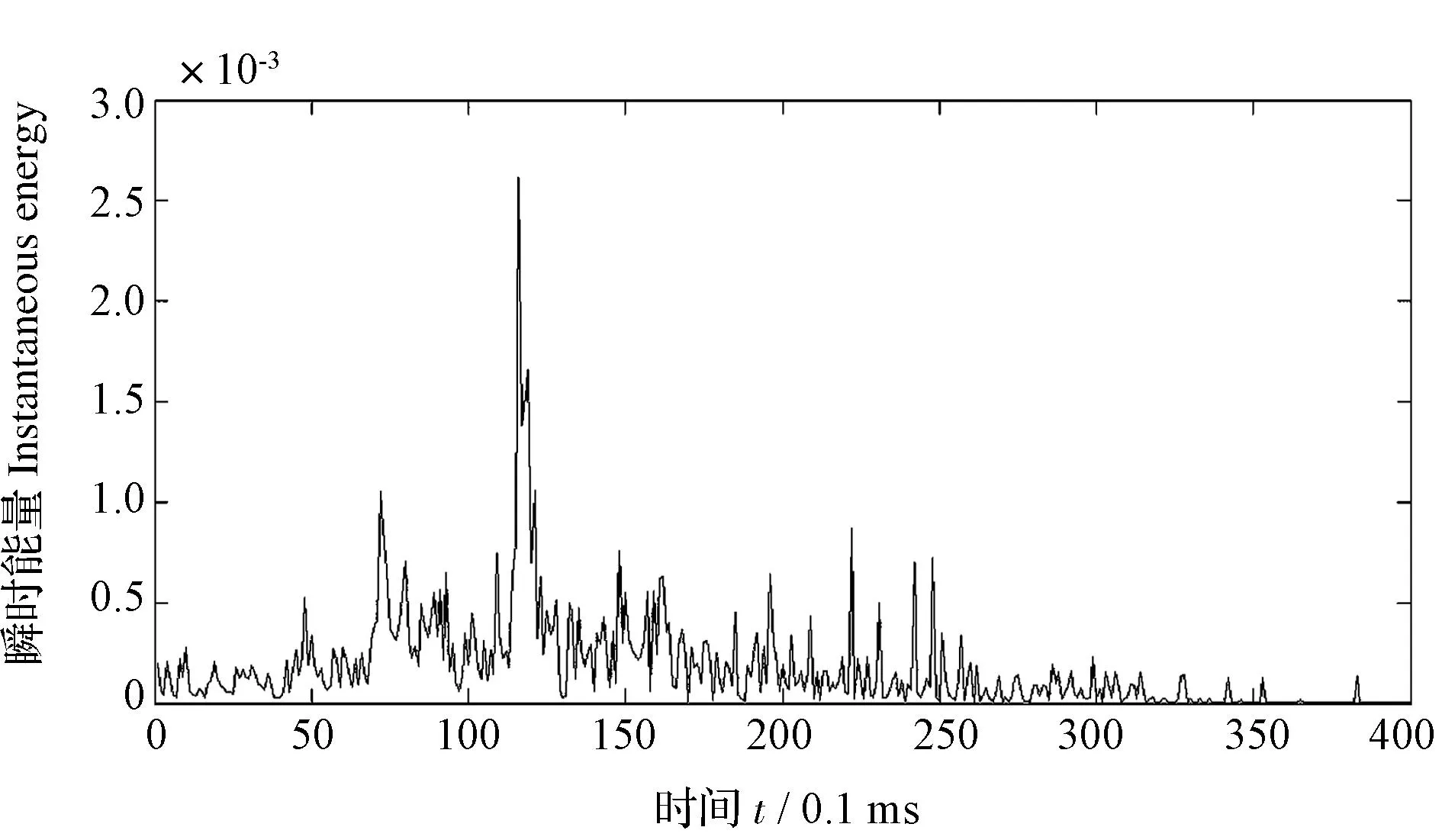
图9　Hilbert边际能量谱Fig.9　Hilbert marginal energy spectrum

图10　瞬时能量分布谱Fig.10　Instantaneous energy spectrum distribution

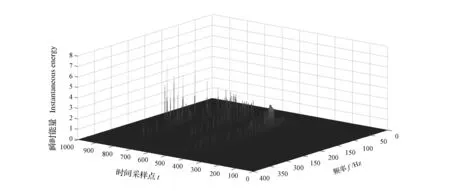
图11　三维能量分布谱Fig.11　Three-dimensional energy spectrum distribution

现阶段对爆破振动信号能量的研究多是分析其中两变量之间的关系，无法同时对三个独立变量进行分析。论文引入爆破振动三维能量谱图，弥补了分析爆破振动信号能量时无法将时间、频率和能量进行同时分析的弊端，在同一坐标系内可以同时分析各IMF分量随时间、频率和能量的分布规律。

从图11爆破振动三维能量谱图可以得知爆破振动能量主要分布在0.3s~1.0s时间段和0~400Hz频率段内，频带100Hz～250Hz中爆破振动分量对应的频带能量达到最大。其分布规律和信号经过EMD分解后产生的结果是相符合的，更加确信的表明HHT方法在爆破振动信号分析中的高效性和适用性。

4结 论

(1)通过分析对比FFT、WT、HHT三种变换方法，表明HHT变换是最新的爆破振动信号时频分析的方法，它摆脱了傅里叶变换理论的约束，将信号自身的固有特征以固有模态函数的形式进行分离，确保了信号被分解后的非平稳性，自动适应能力较强，分解效率较高。

(2)选用HHT变换进行大安山煤矿硬度较大的玄武岩巷道进行双道巷楔形深孔掏槽爆破的爆破振动信号分析，得到三维图直观展示各IMF分量随时间、频率和能量的分布情况。爆破振动能量主要分布在0.3s~1.0s时间段和0~400Hz频率段内，频带100Hz～250Hz中爆破振动分量对应的频带能量达到最大。

(3)对大安山煤矿硬度较大的玄武岩巷道进行双道巷楔形深孔掏槽爆破现场进行爆破振动监测，分析对比数据得出：巷道帮部爆破振动信号的主振方向为Y(切向)方向，巷道底部爆破振动信号主振方向为Z(垂向)方向。

参考文献(References)：

〔1〕中国生，熊正明. 基于小波包能量谱的建(构)筑物爆破地震安全评估[J]. 岩土力学,2010,31(5):1522-1528.

ZHONG Guo-sheng, XIONG Zheng-ming. Safety assessment of structure by blasting seism based on wavelet packet energy spectra[J]. Rock and Soil Mechanics, 2010,31(5):1522-1528.

〔2〕 史秀志，周健，杜坤，等. 爆破振动对民房破坏效应预测的BDA模型及应用[J]. 振动与冲击,2010,29(7):60-65.

SHI Xiu-zhi, ZHOU Jian, DU Kun, et al. BDA model for predicting destructive effect of blast vibration on housing[J]. Journal of Vibration and Shock, 2010,29(7):60-65.

〔3〕 傅洪贤，赵勇，谢晋水，等. 隧道爆破近区爆破振动测试研究[J]. 岩石力学与工程学报,2011,30(2):335-340.

FU Hong-xian, ZHAO Yong, XIE Jin-shui, et al. Study of blasting vibration test of area near tunnel blasting source[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(2):335-340.

〔4〕 蒋复量，周科平，邓红卫，等. 基于小波理论的井下深孔爆破振动信号辨识与能量衰减规律分析[J]. 煤炭学报,2011,36(S2):396-400.

JIANG Fu-liang, ZHOU Ke-ping, DENG Hong-wei, et al. The underground mine′s deep-hole blasting vibration signals identification and energy attenuation law′s analysis based on wavelet theory[J]. Journal of China Coal Society, 2011,36(S2):396-400.

〔5〕 宗琦，汪海波，徐颖，等. 基于HHT方法的煤矿巷道掘进爆破地震波信号分析[J]. 振动与冲击,2013,32(15):116-120.

ZONG Qi, WANG Hai-bo, XU Ying, et al. Analysis of blasting seismic wave signal in coalmine roadway excavation based on HHT method[J]. Journal of Vibration and Shock, 2013,32(15):116-120.

〔6〕 阳生权，廖先葵，刘宝琛，等. 爆破地震安全判据的缺陷与改进[J]. 爆炸与冲击,2001,21(3):223-228.

YANG Sheng-quan, LIAO Xian-kui, LIU Bao-chen, et al. Default of the judging standard of blasting vibration safety abstract[J]. Explosion and Shock Waves, 2001,21(3):223-228.

〔7〕 汪旭光，于亚伦. 关于爆破振动安全判据的几个问题[J]. 工程爆破,2001,7(2):88-92.

WANG Xu-guang, YU Ya-lun. On several problems of safety criterion for blasting vibration[J]. Engineering Blasting, 2001,7(2):88-92.

〔8〕 李夕兵，张义平，刘志祥，等. 爆破振动信号的小波分析与HHT变换[J]. 爆炸与冲击,2005,25(6):529-536.

LI Xi-bing, ZHANG Yi-ping, LIU Zhi-xiang, et al. Wavelet analysis and Hibert Huang transform of blasting vibration signal[J]. Explosion and Shock Waves, 2005,25(6):529-536.

〔9〕 林大超，施惠基，白春华，等. 爆炸地震效应的时频分析[J]. 爆炸与冲击,2003,23(1):31-35.

LIN Da-chao, Shi Hui-ji, BAI Chun-hua, et al. Time-frequency analysis of explosion seismic effects[J]. Explosion and Shock Waves, 2003,23(1):31-35.

〔10〕凌同华，李夕兵. 地下工程爆破振动信号能量分布特征的小波包分析[J]. 爆炸与冲击,2004,24(1):63-68.

LING Tong-hua, LI Xi-bing. The feature of energy distribution for blast vibration signals in underground engineering wavelet packet analysis[J]. Explosion and Shock Waves, 2004,24(1):63-68.

〔11〕 马瑞恒，钱汉明，娄建武，等. 时频分布在爆破振动信号处理中的应用[J]. 工程爆破,2004,10(2):8-12.

Ma Rui-heng, QIAN Han-ming, LOU Jian-wu, et al. Use of time-frequency distributions for processing the signals of blasting vibration[J]. Engineering Blasting, 2004,10(2):8-12.

〔12〕 石崇. 爆破地震效应分析与安全评价[D]. 青岛:山东科技大学,2005.

SHI Chong. Analysis and safety appraisal of blasting seismic effects in far zone[D]. Qingdao: Shandong University of Science and Technology, 2005.

〔13〕 谢全民，龙源，钟明寿，等. 基于小波、小波包两种方法的爆破振动信号对比分析[J]. 工程爆破,2009,15(1):5-9.

XIE Quan-min, LONG Yuan, ZHONG Ming-shou, et al. Comparative analysis of blasting vibration signal based on wavelet and wavelet packets transform[J]. Engineering Blasting,2009,15(1):5-9.

〔14〕 张耀平，曹平，高赛红，等. 爆破振动信号的小波包分解及各频段的能量分布特征[J]. 金属矿山,2007(11):42-43.

ZHANG Yao-ping, CAO Ping, GAO Sai-hong, et al. Wavelet packet decomposition of blasting vibration signals and energy distribution characteristics of frequency bands[J]. Metal Mine,2007(11):42-43.

〔15〕 HUANG W, SHEN Z, HUANG N E. Engineering analysis of biological variables: an example of blood pressure over one day[J]. Proceeding of the National Academy of Science, 1998(95):4816-4821.

HHT Analysis and application of blasting vibration in rock roadway excavation

SUN Qiang， WANG Meng-xiao， XU Yu-shan， LIU Guo-you

(School of Mechanics & Civil Engineering, China University of Mining & Technology(Beijing), Beijing 100083, China)

ABSTRACT：To optimize the blasting parameters and reduce the damage of the surrounding rock， the measured blasting vibration signal of the deep hole cutting blasting in the wedge of the double channel of coal mine was taken as an example. FFT, WT and HHT were compared and time-frequency characteristics and energy distribution of blasting seismic wave signal was analyzed.The analysis showed HHT method could ensure the signal non-stationary after being decomposed. The adaptive ability was the strongest of three and the decomposition efficiency was the highest. The distribution of IMF componented with time, frequency and energy were obtained by HHT method. The results showed that the energy of blasting vibration was mainly distributed in 0.3s~1.0s and 0~400Hz, and band energy corresponding to the blasting vibration componented in 100Hz~250Hz. Through the analysis of the blasting vibration signal, the main vibration direction of the tunnel section and the bottom blasting vibration signal were Z (vertical) direction and Y (tangential) direction were obtained.

KEY WORDS:Rock roadway; Blasting vibration; Vibration signal; HHT; Time frequency; Energy

中图分类号：TD 235； U45

文献标识码：A

doi：10.3969/j.issn.1006-7051.2016.01.001

作者简介：孙 强(1962-)，男，博士、副教授，主要从事岩土工程专业方向的教学与科研工作。E-mail： sunq_208@163.com

基金项目：国家自然科学基金资助项目( 51274203)

收稿日期：2015-10-20

文章编号：1006-7051(2016)01-0001-07