边坡失稳框架结构的安全评估及施工建议

2016-04-19赵莹

河南建材 2016年2期

关键词：黏聚力摩擦角安全系数

赵莹

黄淮学院建筑工程学院（463000）

边坡失稳框架结构的安全评估及施工建议

赵莹

黄淮学院建筑工程学院（463000）

随着山区景点建设项目的不断开发，在边坡上建设办公楼及娱乐设施时有发生，而既建结构整体安全评估因缺乏相应规范一直是工程界的难点之一。文中依托某粉质边坡预修建六层框架办公楼工程实例，采用理论分析、数值模拟和现场实测数据分析等方法，对预建建筑结构和粉质边坡的整体安全稳定性进行研究。并计算出安全系数，以便为同类工程实践提供一定程度上的参考。

边坡；强度折减；破坏过程；安全系数

0 引言

边坡稳定性分析涉及公路、水电、土建等诸多工程领域，是岩土力学问题研究的重要环节内容[1]，亦是工程界研究的重要内容之一。边坡稳定性的分析方法较多，主要包括理论分析、模型实验和数值模拟。理论分析较难准确反映实际工况，模型实验多少缩尺模型[2]，材料的相似性和滑坡机理较难准确量化。随着计算机技术的不断发展，数值模拟成为工程界研究边坡的一个重要趋势。

结合强度折减法建立有限元模型，通过不断折减岩土强度参数黏聚力和摩擦角来计算边坡失稳时的安全系数[3]。失稳判断主要从两个方面综合考虑：一是有限元计算不收敛；二是形成贯通的塑性变形区。利用有限元计算安全系数分为两种：局部安全系数和整体安全系数，边坡稳定性分析多考虑局部安全系数。通过有限元计算边坡的安全系数,可以对易发生滑坡灾害的边坡提出相应的加固措施。

这里结合某土质边坡上6层框架办公楼工程实例，建立二维有限元模型，对修建结构的安全稳定性进行评价。

1 工程概况

图1 立面示意图

某地区边坡上建6层框架办公楼，框架1～2层混凝土等级为C35，3～6层混凝土等级为C30。基础采用柱下钢筋混凝土条形基础。框架与边坡位置剖面图如图1所示。

边坡岩体弹性模量E=120 MPa，泊松比V= 0.32，黏聚力c=13 KPa，摩擦角=22°。

2 有限元模型建立

采用大型通用有限元分析软件ABAQUS建立模型。模型尺寸参考图2。为反映边坡强度折减中破坏面应力集中和位移变化特征，将模型单元局部网格进行细化。边坡采用CPE4R（平面应变缩减实体单元）模拟，框架采用BEAM（梁）单元模拟；模型采用STRUCTURE(结构化分析)划分网格；模型边界条件采用固定约束，两侧限制法向位移。模型网格划分如图3所示。

图2 Mohr-Coulomb模型中的屈服面

图3 模型网格图

模型荷载示意图如图4所示。边坡主要考虑岩体自重，建筑物结构仅考虑自重荷载，对于地震等复杂工况下的荷载组合暂不考虑。有限元模型计算中，边坡岩体采用Mohr-Coulomb本构模型，其他结构采用线弹性本构模型。

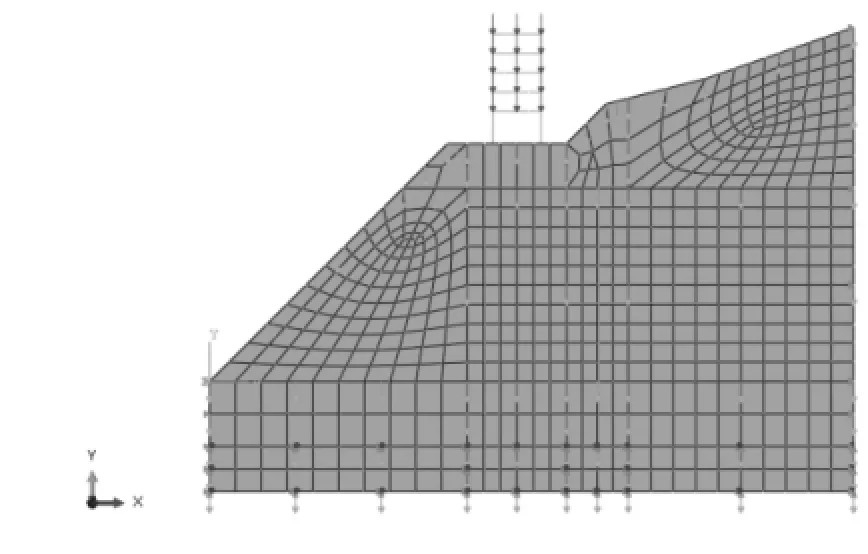
图4 模型荷载图

Mohr-Coulomb屈服面函数为：

式中：φ摩擦角，c为黏聚力，Rmc是控制屈服面在P平面上形状的函数，q是剪应力，p是平均主应力。

3 边坡失稳框架结构安全评估

边坡强度失稳破坏的判据：

1）结构面出现较大位移，且位移变化趋势处于自由状态；

2）形成贯通的塑性区；

3）有限元计算不收敛。

安全系数定义：边坡强度参数由c和φ折减到c'和φ'，则相应的安全系数为：

图5 位移等值线云图

图5是边坡失稳时的位移云图，从图5可知：左侧边坡形成贯通的位移面，且在底角出现最大位移值20 mm；位移滑动面基本位于既建建筑物的桩基下面。图6是边坡失稳时的塑性区云图。结合图6可知：边坡失稳时的破坏面最早位于左侧坡脚。从图7计算安全系数与坡脚位移曲线可知，拐出现点时对应的安全系数为0.72。为保证既建6层框架结构安全，建议施工前采用相应的加固措施。