GENERAL ALGEBROID FUNCTION AND ITS APPLICATION∗

Daochun SUN(孙道椿)School of Mathematics,South China Normal University,Guangzhou 510631,ChinaE-mail:1457330943@qq.comYingying HUO(霍颖莹)School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,ChinaE-mail:fs hyy@aliyun.com,corresponding authorXiaomei ZHANG(张晓梅)Department of Basic Courses,Guangzhou Maritime Institute,Guangzhou 510000,ChinaE-mail:zhangxmcn81@163.com



GENERAL ALGEBROID FUNCTION AND ITS APPLICATION∗

Daochun SUN(孙道椿)
School of Mathematics,South China Normal University,Guangzhou 510631,China
E-mail:1457330943@qq.com
Yingying HUO(霍颖莹)
School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China
E-mail:fs hyy@aliyun.com,corresponding author
Xiaomei ZHANG(张晓梅)
Department of Basic Courses,Guangzhou Maritime Institute,Guangzhou 510000,China
E-mail:zhangxmcn81@163.com

AbstractIn this paper,the authors introduce a kind of reducible algebroid functions,that is general algebroid functions and obtain two fundamental theorems of general algebroid functions.At last,as an application,we generalized a theorem of Li Guoping’s.

Key wordsgeneral algebroid function;the branch point theorem;the first fundamental theorem;the second fundamental theorem

2010 MR Subject Classi fi cation30D30;30D35

∗Received September 14,2014;revised January 12,2015.The second author was supported by the National Natural Science Foundation of China(11201083 and 11501127)and Foundation for Distinguished Young Talents in Higher Education of Guangdong Province(2014KQNCX068).

1 Introduction

Theory of value distribution of algbroid functions was established by Valiron,Ullrich and Selberg in 1930’s[1].Since the domain of an irreducible algebriod function is connected Riemann surface[2],many results on algebroid function are based on the hypothesis that it is irreducible,for example the branch points theorem,Nevanlinna’s first and second fundamental theorem see[1].Other results on singular directions see[3,4].However,it is difficult to judge whether an algebroid function is irreducible or not.What is more,even though an algebroid function is irreducible in some domain,it may be reducible in a smaller domain.That makes us difficult to study the properties of algebroid function.Therefore,one of the author introduced two kinds of reducible algebroid functions:algeboroid functions without multiple factors and general algebroid functions[5].Sun and Gao proved the first fundamental theorem is true for general algebroid function on the complex plane or in the unit disc and the second fundamental theorem for algebroid functions without multiple factors.In 2014,Wang obtained the secondfundamental theorem to general algebroid function on the whole plane,see[6].The purpose of this paper is to study the second fundamental theorem in unit disc and a fundamental inequality in the angular domain for general algebroid function.By these two theorems,we can obtain results on singular directions in[3,4]are also true for general algebroid functions.

We begin with some de finitions and notations of irreducible algebroid function which can be found in[1,5,7].

De finition 1.1A complex function M(z)is called a k-valued irreducible algebroid function in domain D,or an algebraic curve,provided that it satisfies the following irreducible algebraic equation:

where A0(z),A1,···,Ak(z)are k+1 analytic functions in a connected domain D and Ak(z)0.

It is easy to see that the resultant of Ψ(z,M)and its partial derivative ΨW(z,W)verifying R(Ψ,ΨM)(z)0.We say that an algebroid function M(z)is an algeboird function without multiple factors if its resultant R(Ψ,ΨM)(z)0.Obviously,an irreducible algebroid function is also an algebroid function without multiple factors.But an algebroid function without multiple factors may not be an irreducible algebroid function.

For an irreducible algebroid function M(z)in the domain D,points in the sets QM= QM(D):={z∈D;R(Ψ,ΨM)(z)=0},PM(D):={z;Ak(z)=0},SM(D):=PM(D)∪QM(D),TM(D):=D−SM(D)are called multiple points,poles,critical points and regular points,respectively.

For each regular point z0∈TM(D),there are k different regular function elements of M(z),that isAnd for a∈SM(D),there is a critical function element(q(z),Br(a)),where q(z)can be expanded to Pusieux series

in Br(a):={|z−a|＜r}.If u＜0,then(q(z),Br(a))is called a pole element of M(z)(in particular when s=1,it is meromorphic function element).When s＞1,(q(z),Br(a))is an algebraic function element and a is a branch point which multiplicity is s−1.When s=1,u≥0,(q(z),Br(a))is a regular function element.

Next we remind some notations on the theory of value distribution.For an angular domain E=Ω(ψ1,ψ2)=:{z;ψ1＜argz＜ψ2},we denote by n(r,E,M)andthe number of,respectively,poles repeated according to their multiplicities and the distinct poles in{|z|＜r}∩E.Similarly,n(r,E,M=a)is the number of roots of W=a in{|z|＜r}∩E.We shall breviate notation n(r,M)for n(r,C,M).Let nx(r,E,M)be the number of branch points in{|z|＜r}E,counting its multiplicities.Set n1(r,E,M):=

De finition 1.21)Let n(r)be a non-decreasing and positive function on(0,1),the order of n(r)is de fined as

2)If n(r)is de fined on(0,∞),the order of n(r)is de fined as

De finition 1.31)For an irreducible algebroid function M in unit disc,we de fi ne its order as

2)For an irreducible algebroid function M on the whole plane,we de fi ne

In particular,if ρ(W)=∞,then T(r,W)is of in finite order.

De finition 1.4Suppose that M(z)is a k-valued algebroid function de fined in{|z|＜R}.If variable X satisfies the following hypothesis:

(1)if R=+∞and M(z)is of finite order,then

where r→+∞;

(2)if R=+∞and M(z)is of in finite order,then

where r→+∞,outside a set E0of r of finite measure at most;

(3)if R∈(0,+∞),then

where r→R,outside a set E0of r such thatIn particular the above equation holds for some r in the interval(ρ,ρ′)provided that ρ∈(0,R),we denote variable X:=S(r,M).

Many studies on irreducible algebroid function are based on two theorems as follows:

Theorem A[1](the branch points theorem)Suppose M(z)is a k-valued algebroid function de fined by(1.1)in unit disc B:={|z|＜1}(or the whole plane C).Then

Theorem B[1](the second fundamental theorem)Let at(t=1,2,···,p)be p different complex numbers.For a k-valued irreducible algebroid function M(z),we have

1)

where S(r,M)is the error term in De finition 1.4.

In 2012,the authors got a more precise result,which can be used to study the existent of singular direction:

Theorem C[8](a fundamental inequality in the angular domain)Let M(z)be a kvalued irreducible algebroid function in region Ω(φ1,φ2)={z;φ1＜argz＜φ2}(φ1＜φ2).And a1,a2,···,aq(q≥3)are q different complex numbers on the sphere with radius no less thanδ∈(0,1/2).For 0＜ε∗＜ε,φ1＜φ−ε＜φ−ε∗＜φ+ε∗＜φ+ε＜φ2and r＞r∗＞2,we have

In this paper,we will prove that three theorems above are also true for general algeboid functions.

2 General Algebroid Function and Its Propositions

In this section,we introduce the general algebroid function.We begin with its de finition.

De finition 2.1Suppose that the bivariate complex equation(1.1)in D is reducible,or Ψ(z,W)can be decomposed into t prime factors

where each irreducible equation Ψj(z,W)=0 de fines a kj-valued algbroid function Wj(z).Then W(z)is said to be a k-valued(k=k1+k2+···+kt)general algebroid function de fined by(2.1)in D.

By De finition 2.1,we can easily get the regular function elements,pole elements,algebraic function elements,critical points of Wj(z)are also the regular function elements,pole elements,algebraic function elements,critical points of W(z),respectively.The set of all critical points is SW(D):=SW1(D)∪SW2(D)∪···∪SWt(D).And points in TW(D)=D−SW(D)are regular points.

Remarks 11)An irreducible algebroid function is an algebroid function without multiple factors.And an algebroid function without multiple factors is also a general algbroid function.

2)An irreducible algebroid function M(z)has some“good”properties.For instance,it is a single-valued function on its connected Riemann surface.Any two function elements of M(z)must be different.But it is difficult to judge whether an algebroid function is irreducible or not.Even though it is an irreducible algebroid function in a region,it may become reducible in a smaller region,in which its Riemann surface may be unconnected.For example,the algebroid function W de fined by the equation Wk−z=0 is irreducible on the whole plane C.But it is reducible in B=:{|z−2|＜1}.

3)An algebroid function without multiple factors is also a single-valued function on Riemann surface.But its Riemann surface may be unconnected and it can be decomposed into finitely many connected branches.

4)A general algebroid function may be multi-valued on its Riemann surface.And there may be two same connected branches on it.But it is more convenient to study value distribution,which only concerns on the distribution of their values.For a general algebroid function,we need neither to judge whether it is irreducible,nor to judge whether it has multiple factors.

By De finition 2.1,we can obtain two proposition of general algbroid functions as follows:

Proposition 2.2Let W(z)be a general algebroid function de fined by equation(2.1)in a connected domain D.Then W(z)is also a general algebroid function in any connected domain B⊂D.

Proposition 2.3Let W(z)be a general algebroid function de fined by equation(2.1)in a connected domain D and φ be a conformal mapping that maps D to a region B=φ(D).Then W(φ−1(u))is also a general algebroid function in B.

To investigate the structure of general algebroid functions,we introduce a new operation:

De finition 2.4(the union of algebroid functions)Suppose that Wj(z)(j=1,2,···,t,t≥1)are algebroid functions de fined by the equations

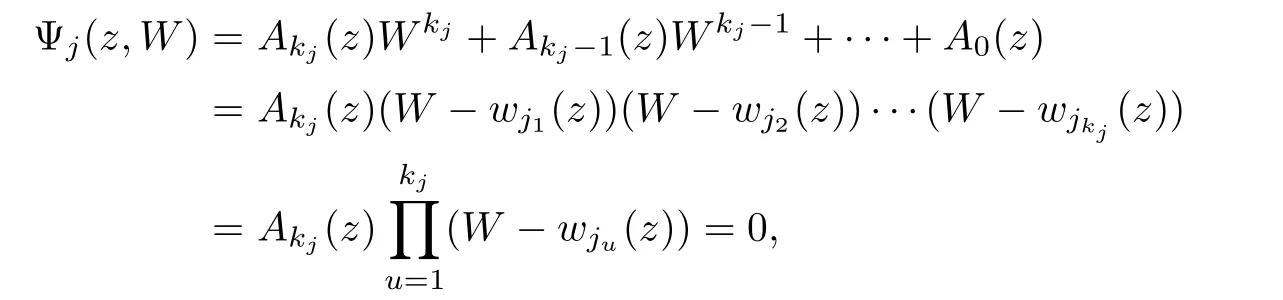
Denoted by

Actually,a general algebroid function is the union of several irreducible algebroid functions.

Proposition 2.5Suppose W1(z),W2(z)are general algebroid function de fined by the following equations,respectively,

Their union

is a(k+v)-valued general algebroid function de fined by

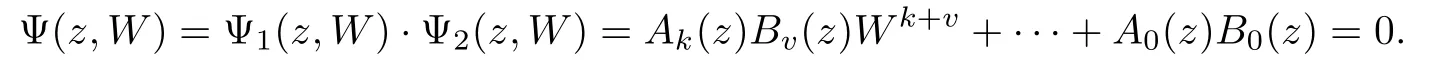
Proof1)For any z0satisfying A(z0)=0,letWe assume that

This completes the proof of Proposition 2.5.

We denote B and C by the unit disc and the whole plane,respectively.And we use the notations m(r,W),n(r,E,W),A(r,E,W),N(r,E,W),and nx(r,E,W),Nx(r,E,W),T(r,E,W),for general algebroid function as we usually do for irreducible algebroid function.

Next proposition is followed from De finition 2.1 and De finition 2.4.

Proposition 2.6Let Wj(z)(j=1,2,···,t,t≥1)be kj-valued general algebroid functions in a disc D:={|z|＜R}(or on the whole plane C).Then for any angular domain E and r∈(0,R),their unionWu(z)is a k-valued general algebroid function(k=k1+k2+···+kt).For any b∈C and r∈[0,R),we have

3 Lemmas

To get the second fundamental theorem of general algebroid function,we still need two lemmas.The following is a result in[6].

Lemma 3.1Wj(z)(j=1,2,···,t,t≥1)is a kj-valued general algebroid function in unit disc B:={|z|＜1}(or on the whole plane C).Let k=k1+k2+···+kt.Then for any r∈(0,R),their unionWu(z)satisfies

1)

2)

3)

By De finition 1.4 and De finition 2.1,we can obtain

Lemma 3.2Let W1(z),W2(z)be two general algebroid functions.If X satisfies the hypothesis in De finition 1.4 of W1(z),or X=S(r,W1).

And there is a constant c1＞0,such that for all r＞0,we have T(r,W2)＞c1T(r,M1).Then X also satisfies the hypothesis in De finition 1.4 of W2(z),or X=S(r,W).

4 Theorems

In investigation of value distribution,the fundamental inequalities and the branch point theorem are often used.Therefore,we now turn to the prove these theorems for general algebroid function.We begin with the branch point theorem:

Theorem 4.1Suppose that W(z)is a k-valued algebroid function de fined by(2.1)in a disc D:={|z|＜R}(or on the whole plane C).Then

where k0:=max{k1,k2,···,kt}.

ProofAccording to De finition 2.1,we have

where Wj(z)is kj-valued irreducible algebroid function in B.In view of Lemma 3.1 and Theorem A,we have

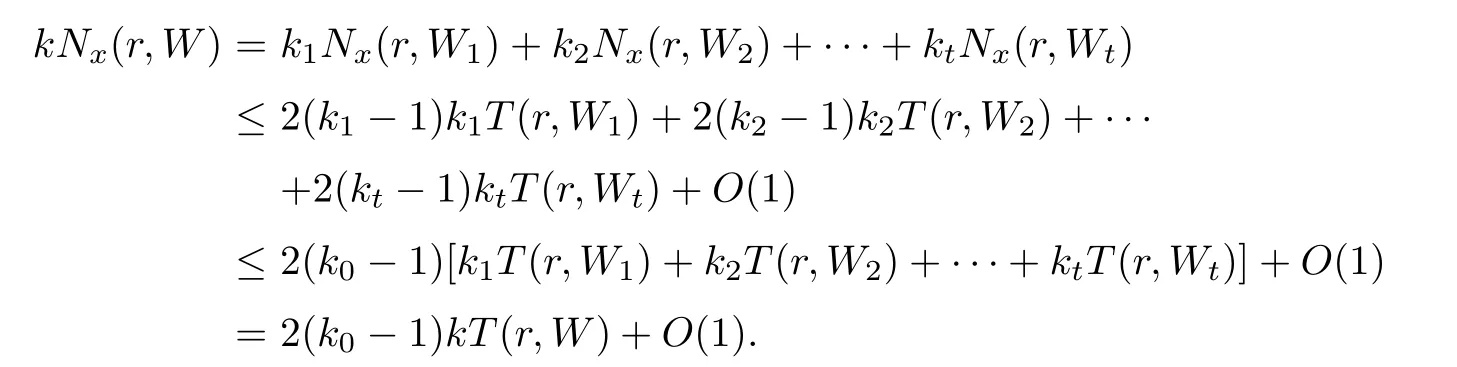
It follows that

Theorem 4.2(the second fundamental theorem of general algebroid function)Assume that W(z)is a k-valued general algebroid function in a disc D:={|z|＜R}(or on the whole plane C)de fined by following equation

Let at(t=1,2,···,p)be p different finite or in finite complex numbers.Then for r∈(0,R),we have

where S(r,W)is the error term in De finition 1.4.

ProofWe use the notations in De finition 1.1.For all j=1,2,···,s,according to Theorem B,Lemmas 3.1 and 3.2,we can obtain that

Combining Theorem 4.1,we have

Similarly,we can obtain

Theorem 4.3(a fundamental inequality in the angular domain)Let W(z)be a k-valued general algebroid function in region Ω(φ1,φ2)=:{z;φ1＜argz＜φ2}(φ1＜φ2).And a1,a2,···,aq(q≥3)are q different complex numbers on the sphere with radius no less thanδ∈(0,1/2).Then for 0＜ε∗＜ε,φ1＜φ−ε＜φ−ε∗＜φ+ε∗＜φ+ε＜φ2and r＞r∗＞2,we have

5 Application

In[9],Li proved that if argz=ψ is a cluster line of meromorphic function f(z)of in finite order concerning some complex number b,then argz=ψ is also a Borel direction.Next we generalize the result to general algebroid function as an application of Theorem 4.2.

First,we introduce the de finition of cluster line and the Borel direction.

De finition 5.1Suppose that W(z)is a k valued algebroid function in the whole plane.

1)Let b be a(finite or in finite)complex number.Then argz=ψ∈[0,2π)is said to be a cluster line of in finite order concerning b,if for all r＞0,M＞0,the following holds

2)If argz=ψis a cluster line of in finite order concerning all b∈C∪{∞}(with 2k exceptional values at most),then argz=ψ is said to be a Borel direction of W(z).

We need the following lemma to obtain the result

Lemma 5.2Suppose η∈[0,2π),t∈(0,π].Mapping

maps the angular domain Ω(η−t,η+t):={|argz−η|＜t}to the unit disc|ω|＜1.Its inverse mapping

maps the unit disc|ω|＜1 to the angular domain Ω(η−t,η+t).Denote z=peiθ.When r is sufficiently large,we have

a)for all σ∈(0,t),

b)

ProofSet φ=θ−η.Since

then

a)Get the maximum on{ω(z);z∈{Ω(η−t+σ,η+t−σ}∩{1/2≤p≤r}}(r＞2):

1)For a sufficiently large number r and a sufficiently small number σ,noting that sinσ∈(2σ/π,σ),we have

2)It follows that

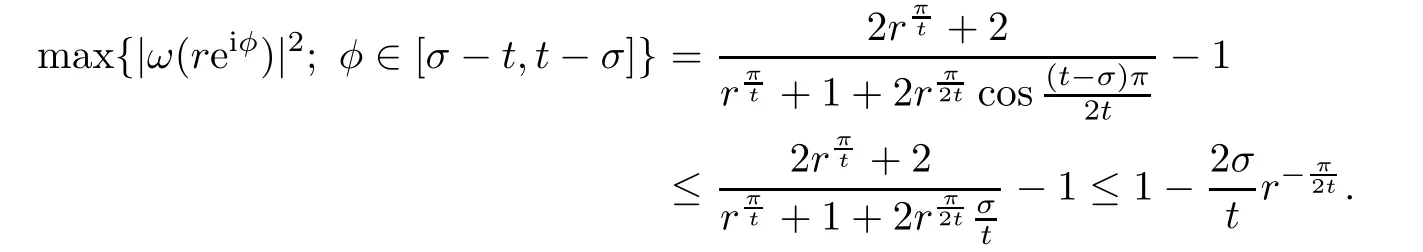
where ctis a constant less than 1 depending on t only.

Combining 1),2)and 3),we have a)holds for any sufficiently large number r.

b)We come to calculate the minimum in Ω(η−t,η+t)∩{0≤p≤r}(r＞1).To get the desire result we just need to obtain the minimum on{reiθ;φ=θ−η∈[−t,t]},

Theorem 5.3Assume b∈C∪{∞}.If argz=ψ is a cluster line of in finite order of a k-valued general algebroid function W(z)concerning b,then argz=ψ is also a Borel direction of in finite order.

Proof1)Let σ＞0 be sufficiently small andThen

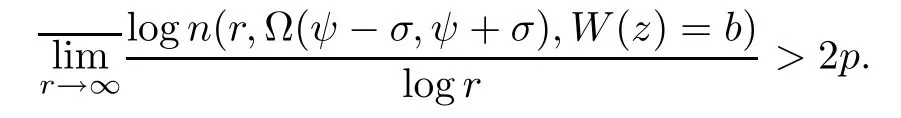
2)Mapping(5.1)maps the angular domain Ω(ψ−2σ,ψ+2σ)to the unit disc B:={|ω|＜1}.Its inverse function is z(w).By Lemma 5.2,a),we have

It implies that the order of n(r,W(z(w))=b)is larger thanin unit disc B.

3)We write n(r)briefly instant of n(r,W(z(w))=b).Applying logand

we can obtain the order of p(N(r,W(z(w))=b))≥−1＞0.

4)From the first fundamental theorem,given that algebroid function W(z(w))may be reducible in unit disc B,

5)By Theorem 4.2,for d complex numbers with at most 2k exceptional values,the order of p(N(r,W(z(w)=d))≥

6)Since

then the order of p(n(r,W(z(w)=d))≥p(N(r,W(z(w)=d))≥

7)It follows from Lemma 5.2,b),we have

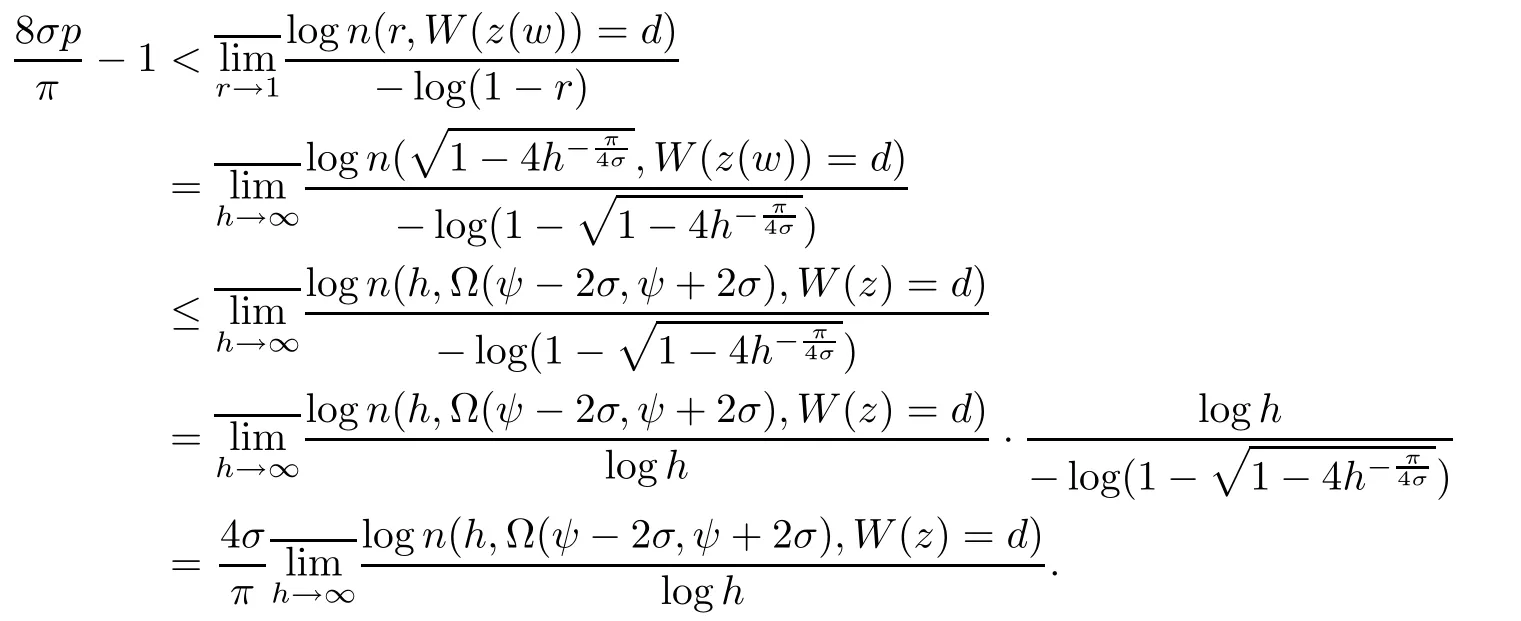
It implies that the order of n(h,Ω(ψ−2σ,ψ+2σ),W(z)=d)is larger than

8)For p is arbitrarily,the ray argz=ψ is a cluster line of W(z)of in finite order concerning d.

This implies that argz=ψ is a Borel direction of W(z).

AcknowledgementsDr.Huo would like to express her gratitude to Pro.Min Wu for giving her a chance to be a visiting scholar in South China University of Technology.

References

[1]He Y Z,Xiao X Z.Algebroial Function and Ordinary Di ff erential(in Chinese).Beijing:Science Press,1988

[2]Lv Y N,Zhang X L.Riemann Surface(in Chinese).Beijing:Science Press,1997

[3]Zhang S H,Zhang X M,Sun D C.The Borel directions of algebroidal function and its coefficent.Acta Math Sci,2014,34B(2):241-251

[4]Huo Y Y,Kong Y Y.On filling discs in the strong Borel direction of algebroid function with finite order.Bull Korean Math Soc,2010,47(6):1213-1224

[5]Sun D C,Gao Z S.Value Distribution of Algebroid Function(in Chinese).Beijing:Science Press,2014

[6]Wang S M.On fudamental theorem of redicible algebroid function.Acta Math Sci,2014,34A:1219-1227

[7]Hayman W K.Meromorphic Functions.Oxford:Clarendon Press,1964

[8]Huo Y Y,Sun D C.A fundamental inequality of the algebroidal function.Abst Appl Anal,2012,2012:Article ID 570324

[9]Li G P.Cluster Line of Meromorphic Function(in Chinese).Wuhan:Wuhan University Press,2007