地形影响下的开采沉陷影响函数法优化
2016-04-18蔡音飞VERDELThierryOLIVIERDeck李晓静
蔡音飞,VERDEL Thierry,OLIVIER Deck,李晓静
(1.太原理工大学 矿业工程学院,山西 太原 030024;2.GeoRessources,Ecole des Mines de Nancy,Université de Lorraine,Nancy 54000;3.山西农业大学 资源环境学院,山西 太谷 030800)
地形影响下的开采沉陷影响函数法优化
蔡音飞1,2,VERDEL Thierry2,OLIVIER Deck2,李晓静3
(1.太原理工大学 矿业工程学院,山西 太原030024;2.GeoRessources,Ecole des Mines de Nancy,Université de Lorraine,Nancy54000;3.山西农业大学 资源环境学院,山西 太谷030800)
摘要:影响函数法广泛应用于地下层状矿体的开采沉陷计算。理论上,该方法适用于水平地表条件下的沉陷预计。将地形变化纳入影响函数法,使此方法可以应用于非水平地表条件下。为了剔除其他开采和地质因素的影响,除地形变化外可能影响沉陷形态的因素都被固定了的简化数值模型被应用于研究中。根据这些数值模拟实验的结果,若干影响函数法的参数,包括影响半径、影响角和下沉率,通过4个地形相关的修正系数被重定义为地表相对矿体高程的函数。优化后的影响函数法可以更好的拟合非水平地表条件下的数值模拟结果和现场观测数据。相较于经典影响函数法,该方法需要将地表点相对矿体的高程作为输入数据。在其他开采、地质条件下,构建简单数值模型的方法可以被用于估算相应条件下的地形影响修正系数。
关键词:影响函数法;数值模拟;影响半径;影响角;下沉率
地下采矿引起的地表沉陷对采区的土地、建筑、道路等的安全和功能造成了不同程度的影响。随着可持续发展的这一科学发展观在国民生产生活中日益得到重视,开采沉陷的研究在矿山生产活动中也显得愈加重要。影响函数法[1-3](含概率积分法)广泛应用于地下层状矿体的开采沉陷预计。国内外有很多专家学者对非水平地表条件下的开采沉陷进行了研究,分析了沉陷规律[4-8],并对影响函数法在受地形影响的开采沉陷计算中的应用提出了一些优化方法[8-11]。这些方法多考虑地质条件与地形的综合影响,导出的公式和参数的选取也相对比较复杂。本文利用数值模拟,考虑近水平矿体开采,并将地形对沉陷的影响单独分离出来,对影响函数法进行优化,改进沉陷计算的结果。相对于经典影响函数法,本方法需将地形作为一个已知输入数据。不同地质条件下的地形影响修正参数的取值可以依据该条件下的数值模拟结果(没有已知参照的情况下),一定程度上避免了人工判断的不确定性。
1经典影响函数法
经典的影响函数法是基于水平地表的,用于计算该条件下地表点的下沉(竖向移动)值。其他的地表移动变形值,包括倾斜、曲率、水平移动、水平变形,都可以通过数学方法由下沉计算。
很多数学函数都可以被用作影响函数,大部分是指数函数[2-3],其中最常用的2个函数的二维表达式列于表1[10]:Knothe等所用的是标准正态分布的概率密度函数,Litwiniszyn等所用的是该函数的变形形式。本质上,一个影响函数描述的是单元开采造成的任一地表点的下沉值,并可由此函数确定单元下沉盆地。某一地表点处由全采区开采造成的下沉是该点处所有单元下沉(由影响函数决定)的累积,见式(1);由于其最大值永远为1(由函数性质决定),需乘上一个系数mq(水平矿体)来调节大小。按此方法可求得所有地表点由全采区开采造成的下沉值。

表1 沉陷计算中常用的影响函数
注:x为地表点横坐标;s为开采单元横坐标;x-s为地表点到开采单元的水平距离;R为单元开采的影响半径,当|x-s| >R时,f(x)极小可忽略;t∈[1,2],由地质条件决定。
由表1中所列的影响函数的数学性质可知,理论上,单元开采的下沉曲线是关于通过该单元的竖轴对称的,水平矿体全采区开采的下沉曲线也是关于通过开采中心的竖轴对称的。
(1)
式中,W为地表点由全采区(包括n个开采单元E1~En)开采引起的下沉值;m为矿体开采厚度;q为下沉率;f(x)为表1所列的任一影响函数。
2地形变化对沉陷影响的数值模拟分析
实际矿山生产活动中,地表沉陷受到很多因素的影响,主要包括开采条件、覆岩条件、地形条件等,难以将地形变化对沉陷的影响单独分离出来,进行研究。所以本文拟使用FLAC3D数值模拟软件,应用一系列简化的数值模型来分析仅地形变化对开采沉陷造成的影响。
FLAC3D是由Itasca公司为岩土工程应用开发的连续介质显式有限差分软件。该软件能较好的模拟岩土体材料的力学行为及材料达到强度或屈服极限时产生的破坏和塑性流动,可应用于大变形情况的模拟,如本文涉及的开挖工程。软件计算所采用的数学模型是根据弹塑性理论的基本原理(应变定义、运动定律、能量守衡定律、平衡方程及理想材料的连续性方程等)建立的[12-13]。本文将采用莫尔-库仑弹塑性材料本构模型进行计算。FLAC3D(包括FLAC)已被广泛应用于各种条件下的沉陷研究,如“三下”开采[13]、急倾斜矿体开采[14]、条带开采[15]、非充分开采[16]等。
(1)模型分层。
研究中,所用模型均由3个地层组成,自下而上分别为底板层、矿体层和覆岩层,其地表倾向主断面如图1所示。
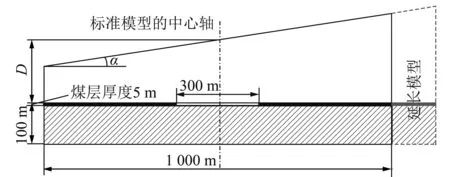
图1 模型分层和尺寸(地表倾向主断面)Fig.1 Strata and dimensions of the models in the middle vertical section along the dip direction of the surface
(2)模型尺寸。
标准模型的平面尺寸为1 000 m×1 000 m,当倾角增大时,地表倾向上山方向的长度会适当延长以保证沉陷边界在模型范围内。模型底板厚度为100 m;矿体厚度为5 m,呈水平层状,开采范围300 m×300 m并位于标准模型正中;覆岩平均厚度D(即矿体平均采深,可由中心轴处地表到矿体竖直距离表示)可变,为100~350 m,上表面倾角α(即地表倾角)可变,为0°~20°。
(3)模型物理力学性质。
模型使用摩尔-库伦模型,各分层的物理、力学性质均固定不变,见表2。覆岩层被简化为一层连续、岩性相同的岩层,其物理、力学性质可用原地层的层厚为权重,采用加权平均法求取。模型的左右边界的横向移动和底部的竖向移动被限制,上表面为自由面,所有内部移动均由自重引起,无附加外力。
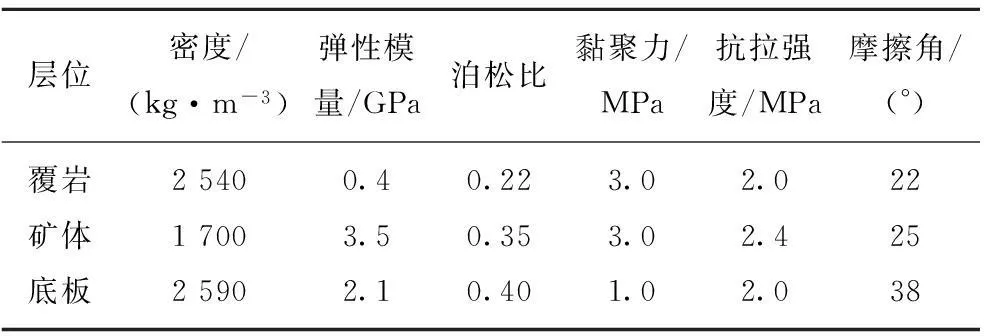
表2 模型的物理和力学性质
简言之,模型中除了地形因素(覆岩的平均厚度和上表面倾角),其他可影响沉陷形态的因素都是固定不变的。地表倾向上山方向的长度增加并不影响沉陷形态。
本文运行了2组数值模拟实验,每组为20个模型,2组间大部分模型可公用。第1组模型,固定平均采深,改变地表倾角;第2组模型,固定地表倾角,改变平均采深。根据结果,地表倾角增加使得下沉和水平移动的数值轻微变大,其形态由原来的对称变为明显的非对称,表现为地表上、下山方向的影响范围不对等和极值位置偏移;平均采深变大使得得下沉和水平移动的数值变小。
3基于数值模拟优化影响函数法
为了将影响函数法用于非水平地表条件下的开采沉陷计算,本节依据上述数值模拟在地表倾向主断面上的结果,对影响函数进行优化。
(1)影响半径R。
表1所列的经典影响函数中,单元开采的影响半径R是常数(图2中R0)。对于倾斜地表,各地表点的影响半径却是不同的[11]:例如图2中,为了计算点Pa由单元Ex开采引起的下沉,其影响半径应取Ra;对于点Pb,其影响半径应取Rb。假设任意地表点相对开采单元的高程已知,为H(x),则任意点的影响半径可由式(2)计算。
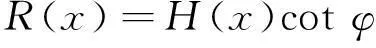
(2)
式中,φ为影响角,定义为开采单元和地表影响边界的连线到水平线的夹角。
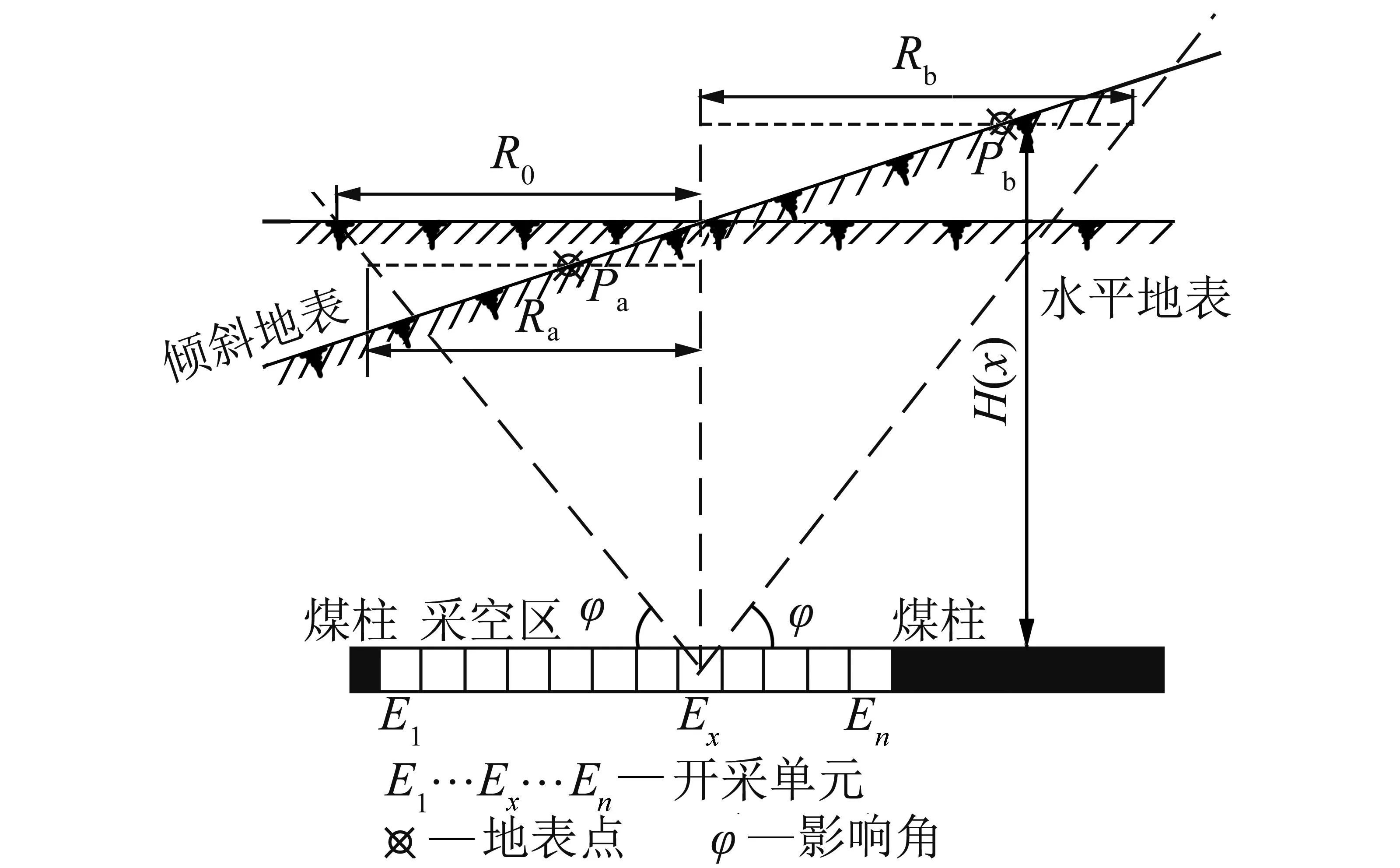
图2 变化的影响半径Fig.2 Varying influence radius for one mining element
(2)影响角φ。
由式(2)可知,非水平地表的影响半径计算时需要考虑影响角。根据对数值模拟结果的分析,发现影响角随开采深度变化不大,其随地表倾角的变化如图3所示。随着地表倾角的增大,地表上山方向的影响角增大,而下山方向的影响角减小,地表上、下山方向的影响角不再相等,其增减幅度与地表倾角成线性关系,见式(3)。由数值模拟结果求得k,c分别为0.27,47.5°。
(3)
式中,φu,φd分别为地表上、下山方向的影响角;k,c为地形变化对影响角的修正系数。
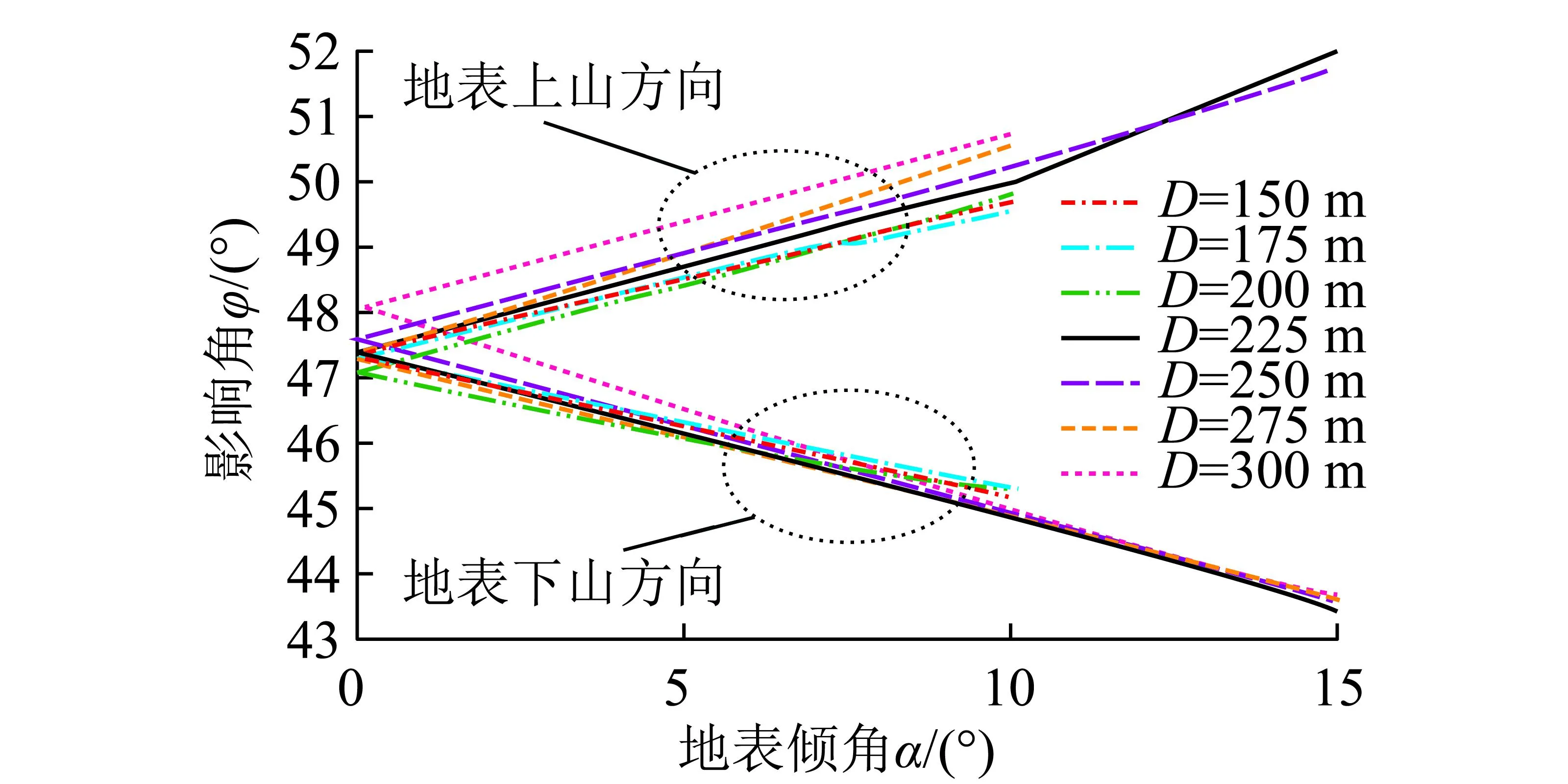
图3 影响角随地表倾角变化规律Fig.3 Variation of the influence angles with the surface dip angle
对于起伏地表,任意地表点的倾角为H(x)导数的反正切函数,见式(4),将其代入式(3),计算起伏地表任意点沉陷时所用的地表上下山影响角应如式(5)所示。

(4)
(5)
将式(5)代入式(2),起伏地表上任意点的影响半径计算公式为分段函数,见式(6)。以图2为例,计算开采单元Ex引起的地表沉陷时,如果地表点在Ex左侧(x
(6)
特别地,水平地表条件下,任意点的α恒为0,H为常数,所以上下山φ相等,R亦相等。
(3)下沉率q。
上文已述,最终下沉的数值需要用下沉率来调整,见式(1)。根据对数值模拟结果的分析,发现下沉率随地表倾角变化不大,其随平均开采深度的变化可见图4,成反比例关系。将该关系应用于地表上任意点,得到下沉率与地表点高程(相对于矿体)的关系,见式(7)。由数值模拟结果求得a,b分别为0.21,44.8。特别地,水平地表条件下,H为常数,q也为定值。
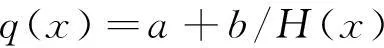
(7)
式中,a,b为地形变化对下沉率的修正系数。
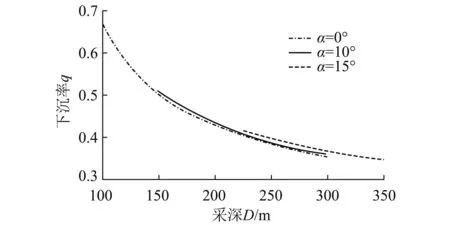
图4 下沉率随平均开采深度变化规律Fig.4 Variation of the vertical subsidence coefficient with the mean mining depth
(4)影响函数法的优化和讨论。
综上所述,将式(6)引入表1所列的影响函数(用R(x)代替R),即可得到针对地形变化优化的影响函数。新函数为分段函数,考虑了地表的变化,包括每个地表点相对矿体的高程和倾角(倾角可由高程函数求导后获得)。将优化的影响函数和式(7)代入式(1),即可得改进的地表任意点受全采区开采影响的下沉值计算公式。其他地表移动变形值的计算沿用经典方法。
上述影响函数法优化算法已在MathematicaTM中编程实现。相较于经典影响函数法,优化方法需要将地表点相对矿体的高程函数作为一个已知数据输入计算。由于地形的影响是本文的研究对象,所以地形函数已知也是研究的前提。
本文引入的4个地形相关的修正系数(a,b,c,k),在不同实例中应用时,需要按照文中方法用数值模拟实验进行验证。由于本文分离了地形的影响,也就是说其他开采、地质条件均为固定不变的,文中提供的这些系数的数值并不适用于所有条件。但应用简化的数值模型求这几个修正系数的方法是通用的。实际中,矿体的上覆岩层往往多于一层,可用他们的物理、力学性质的加权平均(层厚为权重)作为简化的数值模型的覆岩性质。
4结果对比
对于非水平地表,使用变化的影响半径R是必须的,否则无法体现地表高程的变化,计算结果也必然成对称形态。所以此处将优化的影响函数法计算结果(仅调整R或同时调整R,q,φ)与数值模拟结果及现场观测数据进行对比。
(1)与数值模拟结果比较。
本例中数值模型的基本形态如图1所示,地表倾角为15°,平均采深250 m,矿体开采长度300 m。数值模拟结果与优化的影响函数法计算结果(仅调整R或同时调整R,q,φ)对比如图5所示,并统计几者差值的平方和列于表3。
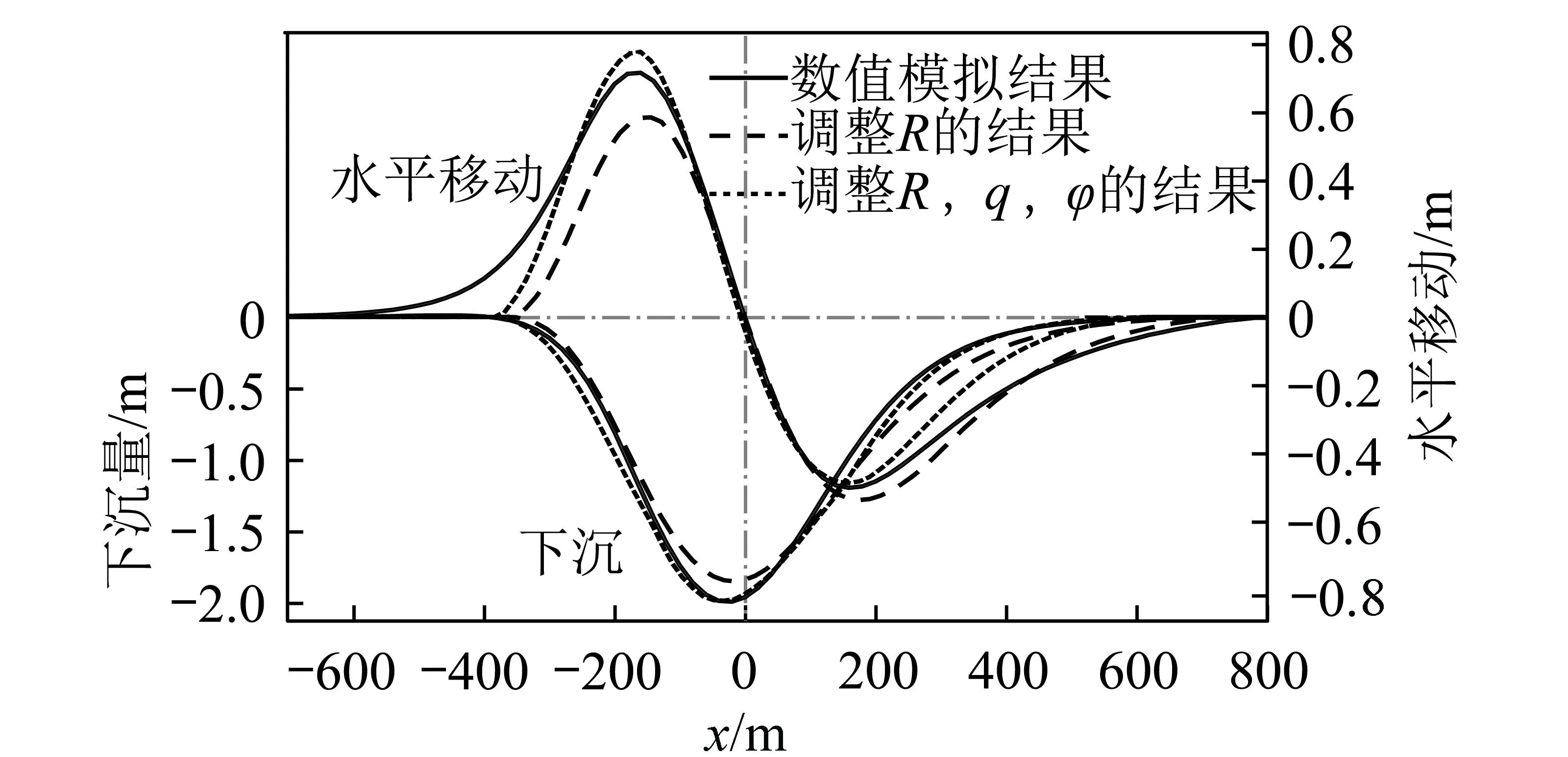
图5 数值模拟结果与优化的影响函数法结果对比Fig.5 Comparison between the subsidence curves obtained from numerical simulation and improved influence function method
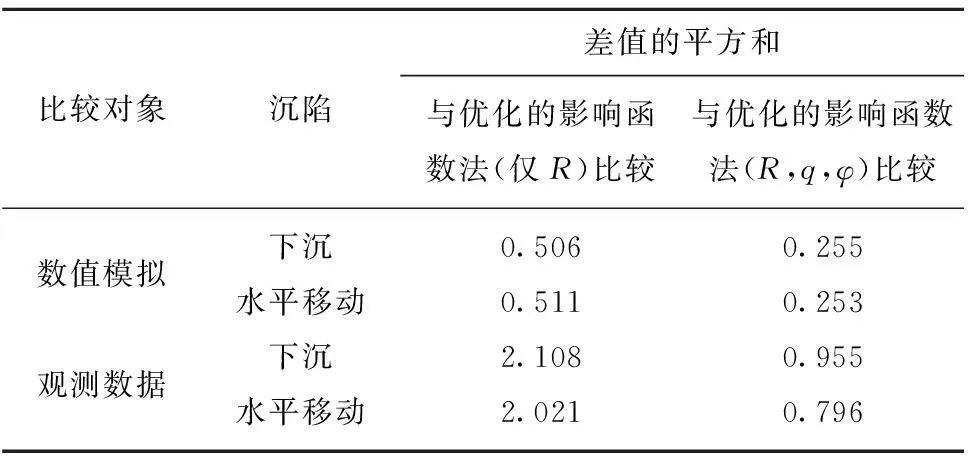
比较对象沉陷差值的平方和与优化的影响函数法(仅R)比较与优化的影响函数法(R,q,φ)比较数值模拟下沉0.5060.255水平移动0.5110.253观测数据下沉2.1080.955水平移动2.0210.796
(2)与现场观测数据[17]比较。
本例中现场观测数据为晋城煤业集团成庄煤矿2307综放工作面倾向观测线的开采沉陷数据。该工作面采用走向长壁综采放顶煤采煤法,走向1 845 m,宽度147.5 m。开采煤层为山西组3号近水平煤层,平均厚度6.7 m,平均开采深度327.8 m。工作面上方地面标高+875~+950 m。现场观测数据与优化的影响函数法计算结果(仅调整R或同时调整R,q,φ)对比如图6所示,并统计几者差值的平方和列于表3。
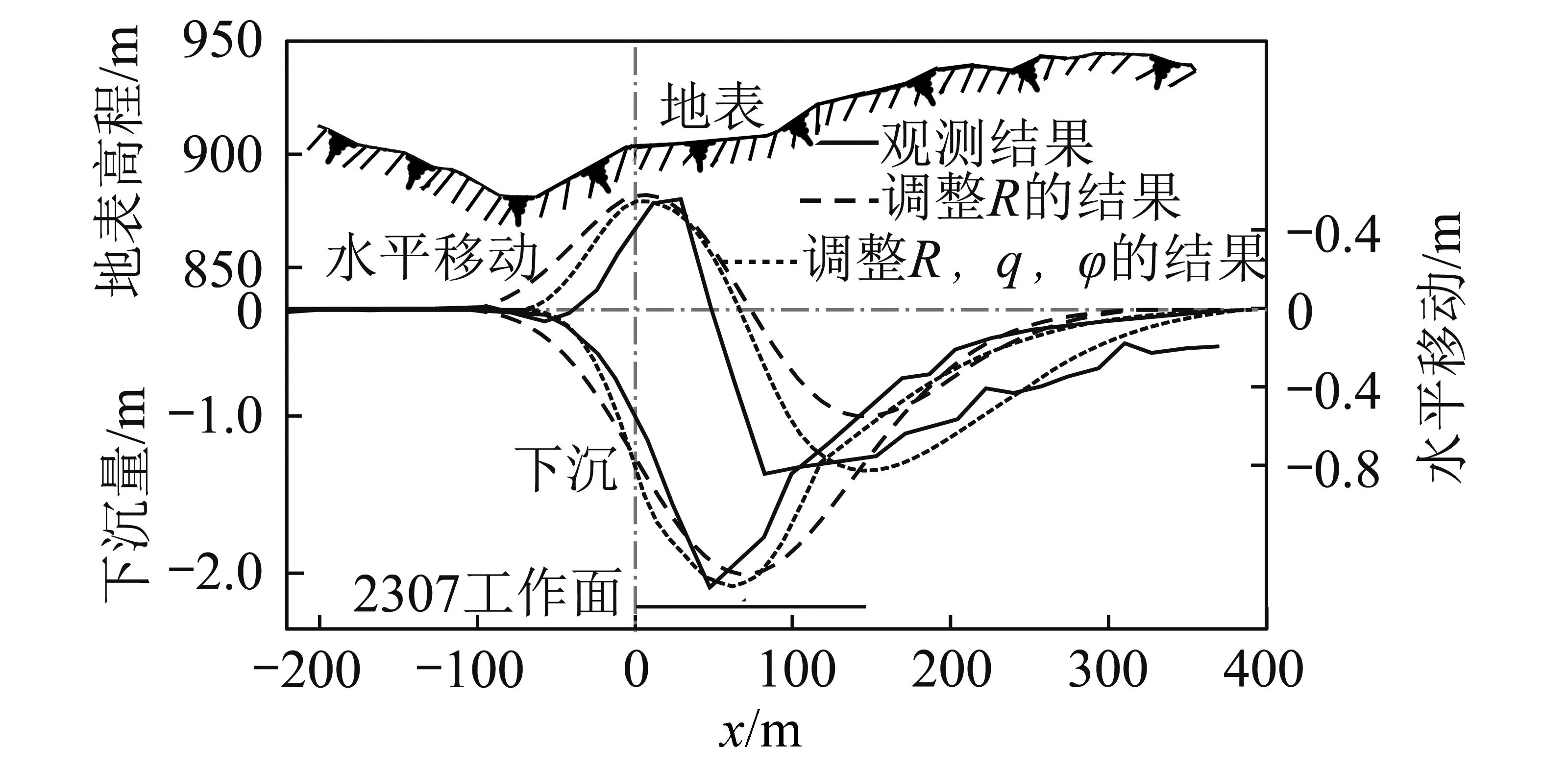
图6 现场观测数据与优化的影响函数法结果对比Fig.6 Comparison between the subsidence curves obtained from field measurement and improved influence function method
由图5,6和表3可见,通过对R,q,φ的调整,影响函数法可以更好的拟合数值模拟结果和现场观测数据。
5结论
(1)提出了一种优化经典影响函数法的方法,使其可以将变化的地表纳入计算。相对于经典方法,改进的方法需考虑地表点相对矿体的高程及其4个地形相关的修正系数。优化后的影响函数为分段函数,可以更好的拟合非水平地形影响下的沉陷曲线。
(2)对数值模型进行了简化,使其仅反映地形的变化。该简化方法具有通用性,可应用于其他开采、地质条件,估算相应条件下的地形影响修正系数。
(3)应用数值模拟结果,修正了若干影响函数法的参数,包括影响半径、影响角和下沉率,他们均可以表示为地表相对高程的函数。
参考文献:
[1]National Coal Board.Subsidence engineers’ handbook[M].London:National Coal Board,1975.
[2]Whittaker N Barry,Reddish J David.Subsidence occurrence,prediction and control[M].Amsterdam,Oxford,New York,Tokyo:Elsevier Science Publishers,1989.
[3]何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[4]Holla L.Ground movement due to longwall mining in high relief areas in New South Wales,Australia[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(4):775-787.
[5]戴华阳,翟厥成,胡友健.山区地表移动的相似模拟实验研究[J].岩石力学与工程学,2000,19(4):1027-1033.
Dai Huayang,Zhai Juecheng,Hu Youjian.Testing study on surface displacement of mountainous region with similar material[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(4):1027-1033.
[6]黄珍珍,吴侃,徐靖.山区地表移动变形规律分析[J].煤炭科技,2007(1):26-29.
Huang Zhenzhen,Wu Kan,Xu Jing.Rules of epidermal deformation in mountainous areas[J].Coal Science and Technology Magazine,2007(1):26-29.
[7]Dai Huayang,Lian Xugang,Liu Jiyan,et al.Model study of deformation induced by fully mechanized caving below a thick loess layer[J].International Journal of Rock Mechanics and Mining Sciences,2010,47:1027-1033.
[8]何万龙.山区开采沉陷与采动损害[M].北京:中国科技出版社,2003.
[9]戴华阳.负指数函数法预计山区地表移动[J].矿山测量,1990(3):48-51.
Dai Huayang.Mountains mining subsidence prediction by negative exponent method[J].Mining Surveying,1990(3):48-51.
[10]Cai Yinfei,Verdel Thierry,Deck Olivier.On the topography influence on subsidence due to horizontal underground mining using the influence function method[J].Computers and Geotechnics,2014,61:328-340.
[11]Saeidi Ali.The vulnerability of structures subjected to hazards caused by ground movements:Development of a simulator for damages[D].Nancy:Ecole des Mines,2010.
[12]谢和平,周宏伟,王金安,等.FLAC在煤矿开采沉陷预测中的应用及对比分析[J].岩石力学与工程学报,1999,18(4):397-401.
Xie Heping,Zhou Hongwei,Wang Jin’an,et al.Application on FLAC to predict ground surface displacements due to coal extraction and its comparative analysis[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(4):397-401.
[13]王生俊,贾学民,韩文峰,等.高速公路下伏采空区剩余沉降量 FLAC3D计算方法[J].岩石力学与工程学报,2005,24(19):3545-3550.
Wang Shengjun,Jia Xuemin,Han Wenfeng,et al.A FLAC3Dmethod for calculation of residual subsidence in a mining area beneath an expressway[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(19):3545-3550.
[14]高明中,余忠林.急倾斜煤层开采对地表沉陷影响的数值模拟[J].煤炭学报,2004,28(6):578-582.
Gao Mingzhong,Yu Zhonglin.Numerical analysis of surface subsidence behavior relative to steep excavation[J].Journal of China Coal Society,2004,28(6):578-582.
[15]袁坚,冯涛,刘金海,等.条带采宽及留宽对地表沉陷影响的研究[J].采矿与安全工程学报,2007,24(1):88-91.
Yuan Jian,Feng Tao,Liu Jinhai,et al.Effect of mining width and retaining width on ground subsidence[J].Journal of Mining & Safety Engineering,2007,24(1):88-91.
[16]郭俊廷,阎跃观,戴华阳,等.基于FLAC3D的非充分采动地表移动求参方法[J].矿业工程研究,2010,25(4):43-46.
Guo Junting,Yan Yueguan,Dai Huayang,et al.Determination of ground movement permanents under insufficient mining condition based on simulation results of FLAC3D[J].Mineral Engineering Research,2010,25(4):43-46.
[17]宋新华,邓喀中,阎跃观,等.地形对地表移动变形的影响分析[J].矿山测量,2007(3):70-72.
Song Xinhua,Deng Kazhong,Yan Yueguan,et al.Analysis of topography influence on ground displacement and deformation[J].Mining Surveying,2007(3):70-72.
Improving the influence function method to take topography into the calculation of mining subsidence
CAI Yin-fei1,2,VERDEL Thierry2,OLIVIER Deck2,LI Xiao-jing3
(1.CollegeofMiningEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China;2.GeoRessources,EcoledesMinesdeNancy,UniversitedeLorraine,Nancy54000,France;3.CollegeofResourcesandEnvironment,ShanxiAgriculturalUniversity,Taigu030800,China)
Abstract:The classic influence function method is often used in the calculation of mining subsidence caused by stratiform underground excavations.Theoretically,its use is limited to the subsidence predictions under the condition of horizontal ground surface.In order to improve the original influence function method to take topographic variations into account.Due to real-world mining conditions that are usually complicated,it is difficult to separate topography influences from influences caused by other factors.The present work uses simplified numerical simulation models to analyze the topography influence only,avoiding the effects of other factors.Then several parameters of the influence function method,including the influence radius,influence angle,and vertical subsidence coefficient,are adjusted by considering four correction factors with respect to the topography.They all can be defined as functions of the relative surface elevations with ore body.After this,the improved influence function method can well fit the numerical simulation results and field measurement data.Comparing to the original method,the improved method only takes the topography as additional input data.The method of constructing the simplified numerical simulation models can be used to solve the topographic correction factors under other mining and geological conditions.
Key words:influence function method;numerical simulation;influence radius;influence angle;vertical subsidence coefficient
中图分类号:TD325.2
文献标志码:A
文章编号:0253-9993(2016)01-0271-06
作者简介:蔡音飞(1983—),男,浙江嘉兴人,讲师,博士。E-mail:caiyinfeimines@163.com,yinfei.cai@univ-lorraine.fr
收稿日期:2014-12-15修回日期:2015-01-19责任编辑:常琛
蔡音飞,VERDEL Thierry,OLIVIER Deck,等.地形影响下的开采沉陷影响函数法优化[J].煤炭学报,2016,41(1):271-276.doi:10.13225/j.cnki.jccs.2014.1736
Cai Yinfei,Verdel Thierry,Olivier Deck,et al.Improving the influence function method to take topography into the calculation of mining subsidence[J].Journal of China Coal Society,2016,41(1):271-276.doi:10.13225/j.cnki.jccs.2014.1736
