基于脆性模量系数的岩石应变软化及渗透率演化模型

张春会,岳宏亮,王来贵,郭晓康,于永江

(1.河北科技大学 建筑工程学院，河北 石家庄　050018；2.辽宁工程技术大学 力学与工程学院，辽宁 阜新　123000)



基于脆性模量系数的岩石应变软化及渗透率演化模型

张春会1,2,岳宏亮1,王来贵2,郭晓康1,于永江2

(1.河北科技大学 建筑工程学院，河北 石家庄050018；2.辽宁工程技术大学 力学与工程学院，辽宁 阜新123000)

摘要:岩石峰后应变软化力学行为及渗透率演化规律是岩石工程稳定性和安全性分析的基础。在三轴实验基础上分析了围压对岩石峰后应变软化力学行为的影响规律，提出了描述围压对岩石峰后脆性影响的新参数，即脆性模量和脆性模量系数，分析了脆性模量的物理意义和脆性模量系数方法的应用范围。基于脆性模量系数，结合强度退化指数、扩容指数、FLAC中的SS模型和体积应变增透率，建立了考虑围压影响的岩石应变软化模型和渗透率演化模型。利用本文模型较好地模拟再现了不同围压下Gebdykes白云岩变形和巴里坤砂岩渗透率的演化过程，验证了本文模型的合理性。将本文模型应用于某煤层开采过程中围岩变形和渗透率的动态演化预测，结果表明随着煤层开采，采动应力引起围岩变形、破坏，其渗透率也随之动态变化，本文模型能较好地再现煤层开采过程中围岩的渗透率动态演化规律。

关键词:脆性模量系数;体积应变增透率;渗透率演化;应变软化

岩石峰后应变软化力学行为及渗透性演化规律是隧道开挖、煤炭开采、煤层气和页岩气开发、固体废弃物处理、地下储库建设、岩爆灾害预报与防治等诸多岩石工程安全性和稳定性分析的基础[1-4]。

岩石是一种地质体，遭受地应力作用。地应力对岩石的峰后力学行为影响很大。岩石三轴实验是研究地应力对岩石力学行为影响的重要手段[5-8]，实验中使用围压模拟地应力。作为一种地质体，天然岩石内通常含有孔隙微裂隙等尺度不一的缺陷，三轴压缩下这些内部缺陷、张开、闭合、发育和汇聚，使得岩石的变形一般呈非线性特征，但为研究方便，通常对其进行适当简化[9-16]。依据岩石三轴试验结果[5-8]和已有研究[9-10,12-16]，岩石在不同围压下的力学行为可简化如图1所示。

图1(a)为简化的岩石应力应变曲线，包括3个阶段：① 线弹性阶段OA。在这一阶段忽略了初始压密阶段和岩石屈服点至峰值强度之间的应变硬化阶段。② 强度退化阶段AB。当岩石的强度达到峰值强度后，岩石内微裂隙、裂隙汇聚成核，岩石破坏，试验机再轴向压缩，岩石的承载能力降低，并逐渐降低至残余强度。③ 残余塑性流动阶段。当岩石的强度降至残余强度后，岩石的残余强度基本不变，岩石近似塑性流动状态。

图1(b)将三轴压缩岩样体积应变与轴向应变之间的关系简化为2个阶段。在线弹性阶段，随着轴向加载，岩石的体积压缩。当岩石的应力达到峰值强度，岩石破坏，并发生体积扩容。实验研究表明[9,15-16]，当应力达到屈服点附近岩石的剪胀就开始发生，但从屈服点至峰值强度，剪胀扩容缓慢，在峰值强度附近才开始快速增长。因此，在图1(b)中假设剪胀在峰值强度才开始发生，这一假设也为许多学者所采用[10,12,15-16]。围压将限制岩石内的裂隙扩展，因此随着围压增加，岩石的剪胀扩容速率趋缓。

图1(c)将渗透率与轴向应变的关系简化成2阶段，并与体积应变的变化相对应，这主要是由于：渗透率是岩石内孔隙空间的函数，孔隙空间越大，渗透率越大。岩石固体颗粒的体积变化微小，承载岩石的胀缩实质是孔隙空间的胀缩，体积应变反映了岩石孔隙空间的变化，因此体积应变与岩石的渗透率之间具有紧密的正相关性，这已为实验结果所证实[9,12,17-19]。

图1　简化岩石三轴应力-应变-体积应变-渗透率曲线Fig.1　Simplified stress-strain-volumetric strain-permeability curves under tri-axial compression

总体上，围压对岩石力学行为的影响主要包括如下几个方面：

(1)随着围压增加，岩石的峰值强度增长，破坏应变增大。

(2)随着围压增加，岩石残余强度增大，峰后强度降低。

(3)当应力达到岩石的峰值强度，岩石开始发生剪胀扩容。随着围压增加，岩石的剪胀扩容减弱，高围压下岩石峰后变形呈理想塑性，体积扩容基本消失。

(4)随着围压增加，岩石峰后强度退化速率趋缓，即岩石的塑性增强，脆性减弱。

(5)岩石的渗透率变化与体积应变密切相关[9,12,17-19]。在弹性阶段，岩石体积压缩，渗透率降低，岩石破坏后，岩石内裂隙、微裂隙扩展、汇聚，岩石剪胀扩容，渗透率增长。

为描述上述围压对岩石力学行为的影响规律，国内外学者开展了大量研究。围压对岩石峰值强度和破坏应变的影响，通常使用强度准则来描述，例如Mohr-Column准则、Hoek-Brown准则等。Fang等[13-14]提出了强度退化指数的概念来描述围压对岩石残余强度的影响。Yuan等[15-16]研究了围压对岩石剪胀扩容的影响，提出使用扩容指数来描述围压对岩石剪胀扩容的影响。张春会等[12]、薛东杰等[17]、Cai等[18]、Chen等[19]通过实验研究了岩石变形与渗透率之间的关系。Zhao等[11]注意到岩石峰后剪胀扩容不会无限发展，提出了动态剪胀角方法。于永江等[10]提出了一个承载围岩的渗透率演化模型，但在这个模型中围岩单元的渗透率受到单元尺寸的影响。谢和平等[20]提出了采动煤层增透率的理论模型。

以往研究主要涵盖了岩石力学行为的(1)、(2)，(3)和(5)方面，但没有考虑围压对岩石峰后强度退化过程的影响。实验研究结果表明，围压对岩石峰后强度退化过程有很大影响，随着围压增加，岩石峰后强度退化速率趋缓。若忽视围压对岩石峰后强度退化过程的影响，将会对岩石变形和破坏区估算产生很大影响。Tang等[21]的细观损伤力学方法可以定性模拟岩石的应变软化行为，但预测结果与三轴实验结果偏差较大。Tan等[9]使用FLAC中的Hoek-Brown模型模拟岩石的峰后应变软化和渗透率演化，但该方法缺乏明确的物理意义，且过程复杂。张春会等[12]初步提出了脆性模量的概念，并将其用于描述三轴压缩岩样的峰后力学行为，但研究尚不完善。

本文在三轴实验成果分析基础上，提出了脆性模量和脆性模量系数的概念，分析了脆性模量的物理意义和脆性模量系数方法的适用范围。以脆性模量系数为基础，结合强度退化指数、扩容指数、FLAC中的SS模型和岩石体积应变增透率方法，建立了一个描述岩石变形破坏全过程的应变软化和渗透率演化模型。将该模型应用于某煤层开采过程中煤岩的渗透率演化预测，取得了较好结果，从而为岩石应变软化及渗透率演化模拟提供了一种方法。

1应变软化模型

1.1脆性模量及脆性模量系数

简化的岩石三轴应力应变曲线如图1所示。在图1中，将∠ABF的正切值定义为脆性模量。根据图1，脆性模量[12]可以表示为

(1)

式中，δσ为岩石峰后强度降，为峰值强度与残余强度的差值；ε1p为岩石由峰值强度降至残余强度的轴向塑性应变(图1)。

脆性模量描述了岩石峰后强度跌落速度的快慢，脆性模量越大，岩石峰后强度跌落速度越快，岩石峰后越表现为脆性特征；脆性模量越小，岩石峰后强度跌落速度越慢，岩石峰后越表现为塑性特征。

脆性模量系数[12]定义为

(2)

式中，Eb0为单轴压缩下岩石的脆性模量；Eb为某围压下岩石的峰后脆性模量。

很明显，在单轴条件下脆性模量系数为1，随着围压增加，岩石塑性增强，脆性减弱，脆性模量减小，脆性模量系数减小，在脆延转化围压时，岩石变形呈理想塑性特征，脆性模量系数近似为0。图2示意了围压对脆性模量系数的影响规律。

图2　围压与脆性模量系数的关系Fig.2　Relationship between confining pressure and brittle modulus coefficient

为了获得围压与脆性模量系数之间的数学关系，对不同种类岩石如粗粒大理岩[6]、红砂岩[7]、鲍店煤[8]、Gebdykes白云岩[15]的三轴实验数据整理，获得了不同类别岩石围压与脆性模量系数的实验数据，见表1。笔者等[12]还给出了巴里坤砂岩、Tennessee大理岩和山西含碳泥岩的相应实验数据。对这些数据进行统计分析可以推定，围压与脆性模量系数之间近似符合负指数函数关系：

(3)

式中，nb为试验拟合常数；σ3为围压。

利用式(3)拟合表1中围压与脆性模量系数的关系，结果如图3所示。从图3可见，式(3)较好地描述了围压与脆性模量系数之间的关系。

由表1结合文献[12]还可以看出，脆性模量系数方法主要应用于砂岩、泥岩等中硬或软弱的岩石，这些岩石单轴条件下的应力应变曲线为I型[22]。对于单轴条件下应力应变曲线为II型的硬脆岩石，单轴脆性模量为负值，本方法不适用。

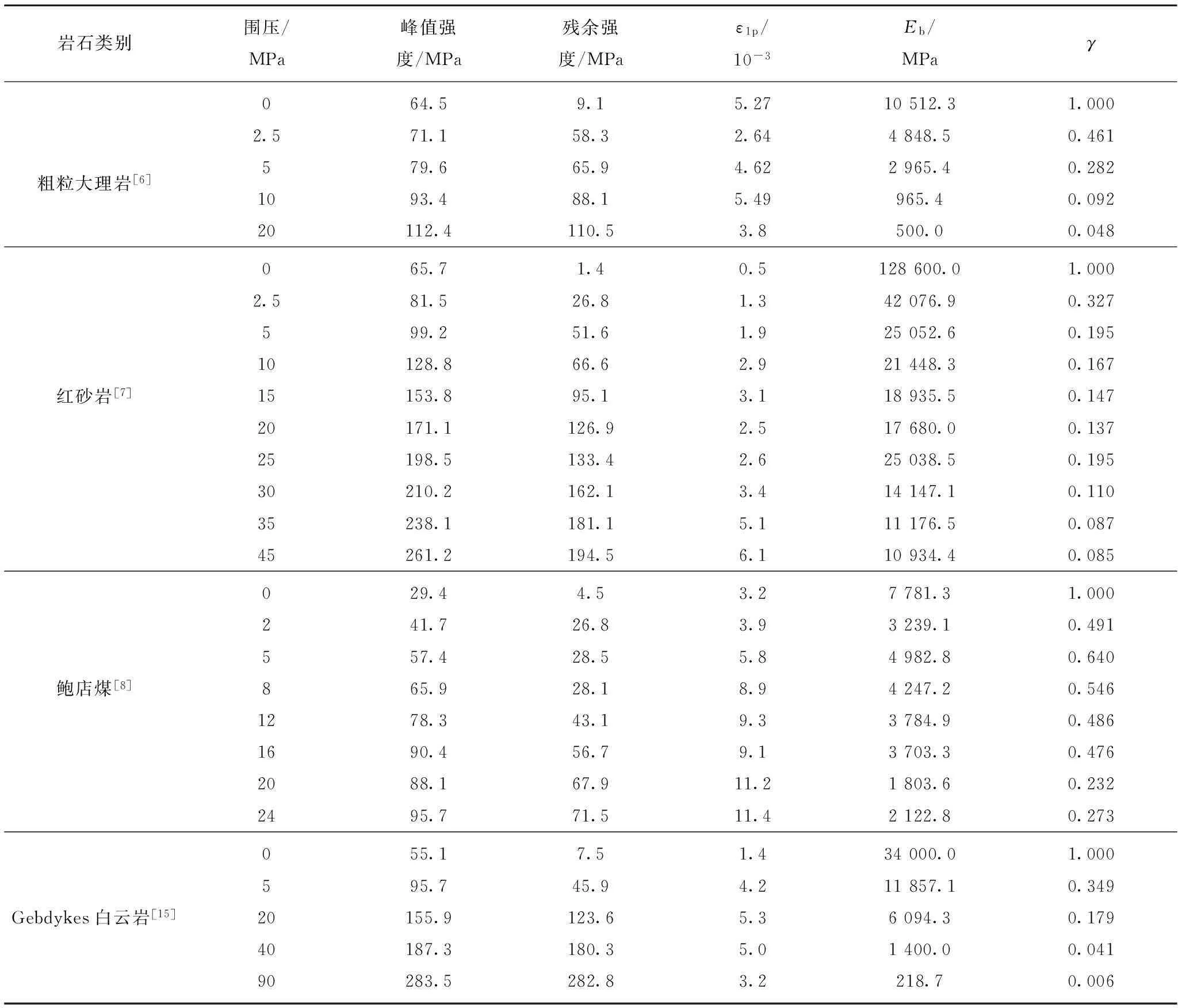
表1　不同岩石的围压与脆性模量系数

图3　不同岩石脆性模量系数与围压的关系[6-8,15]Fig.3　Relationship between brittle modulus coefficient and confining pressure

1.2残余强度

Fang等[13-14]在三轴实验基础上，提出的强度退化指数描述围压对岩石残余强度的影响。强度退化指数rd与围压的关系[13]可表示为

(4)

式中，nd为三轴实验数据拟合常数。

于是，围压σ3下岩石的残余强度[13]可表示为

(5)

式中，σr为残余强度；δσu为单轴强度降；σ1为围压σ3时的峰值强度；σc为单轴抗压强度。

由莫尔-库伦强度准则，岩石的峰值强度σ1可表示为

(6)

式中，k=(1+sinφ)/(1-sinφ)；φ为内摩擦角；c为黏聚力。

假设岩石的残余强度仍服从莫尔-库伦准则，于是岩石的残余强度可表示为

(7)

式中，kr=(1+sinφr)/(1-sinφr),φr为峰后残余内摩擦角；cr为峰后残余黏聚力。

式(7)中的残余内摩擦角和残余黏聚力由围压与残余强度之间的关系通过数据拟合确定。

1.3剪胀扩容

Yuan等[15-16]定义了扩容指数来描述围压对剪胀扩容的影响，扩容指数Id与围压之间符合如下经验关系[15]：

(8)

式中，σh为无剪胀时的围压值，该值通常取脆延转化围压；md为三轴实验数据拟合常数。

扩容指数[15]可以表示为

(9)

式中，Δεvp为塑性体应变；Δε1p为塑性轴应变；下标“0”和“p”分别代表单轴和围压σ3时的情况；θ为塑性轴应变与塑性体应变之间的夹角，如图1(b)所示。

根据剪胀角的定义，θ与岩石剪胀角ψ的关系[15]可表示为

(10)

结合式(9)，在围压σ3时的剪胀角可以表示为

(11)

θ0可以表示为

(12)

式中，ψ0为单轴条件下岩石的剪胀角。

式(11)和(12)描述了围压对岩石剪胀角的影响。

1.4应变软化模型

基于脆性模量系数、强度退化指数、扩容指数，结合FLAC[23]中的SS模型(strain-hardening/softening model)，可以建立考虑围压影响的岩石应变软化力学模型，具体如下：在峰值强度前，岩石为线弹性材料，服从广义胡克定律。当岩石应力达到峰值强度，岩石破坏，发生强度退化，达到残余强度后进入塑性流动阶段。残余强度由式(5)计算，残余内摩擦角和残余黏聚力由围压与残余强度的实验数据，结合式(7)拟合确定。若岩石破坏，发生剪胀，利用扩容指数和式(11)计算不同围压下的剪胀角。利用脆性模量系数描述围压对岩石峰后脆性的影响。

将上述3个指数与FLAC[23]内嵌的SS模型结合。在SS模型中，使用表(table)函数来描述岩石峰后的应变软化过程。本文使用的内摩擦角和黏聚力的表函数形式如图4所示[12]，其中φ0和c0为岩石内摩擦角和黏聚力，φr和cr为残余内摩擦角和残余黏聚力。为定义从φ0和c0退化至φr和cr的过程，需要等效塑性应变εps。

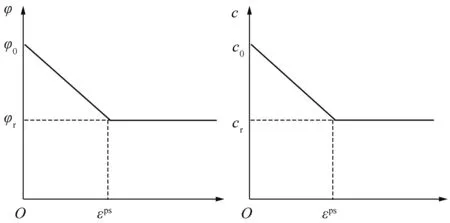
图4　内摩擦角和黏聚力退化Fig.4　Degradation of internal friction angle and cohesion

基于脆性模量系数和轴向塑性应变，FLAC中SS模型的等效塑性应变可以表示[12]为

(13)

式中，Nψ=(1+sinψp)/(1-sinψp)，ψp为σ3围压时的剪胀角，利用式(11)计算。

2渗透率演化模型

大量实验研究结果表明[9,12,17-19]，岩石的渗透率是一个与体积应变正相关的动态场变量。渗透率η可以表示为体积应变的函数，即可以写为[12,24]：

(14)

式中，η0为初始渗透率；η为渗透率；εV为体积应变。

体积应变增透率λ定义为

(15)

λ的物理意义为单位体积应变改变率引起的渗透率增量。

于是，式(14)可写为

(16)

λ可取为如下多项式形式：

(17)

式中，a0,a1,a2，……为拟合常数，由渗透率与体积应变实验数据对拟合确定。

3数值实现

利用FLAC的FISH函数方法实现考虑围压影响的岩石应变软化和渗透率演化模型，具体实现过程为

(1)根据分析的工程问题，构建模型，划分计算网格，定义初边值条件，赋值nb，nd，md，σh等实验数据拟合参数。

(2)将模型中的岩石指定为弹性材料，进行初应力分析。

(3)将模型中的岩石本构模型修改为SS模型，不改变体积模量和剪切模量，根据单元应力计算强度退化指数、扩容指数、脆性模量系数，计算残余内摩擦角、残余黏聚力、剪胀角、等效塑性应变，为SS模型中的参数赋值。

(4)进行开挖或加载计算分析，每20时步根据单元应力重新计算上述参数，由单元体积应变根据式(16)计算渗透率。

(5)重复上述过程，输出计算结果。

具体实现框图如图5所示。

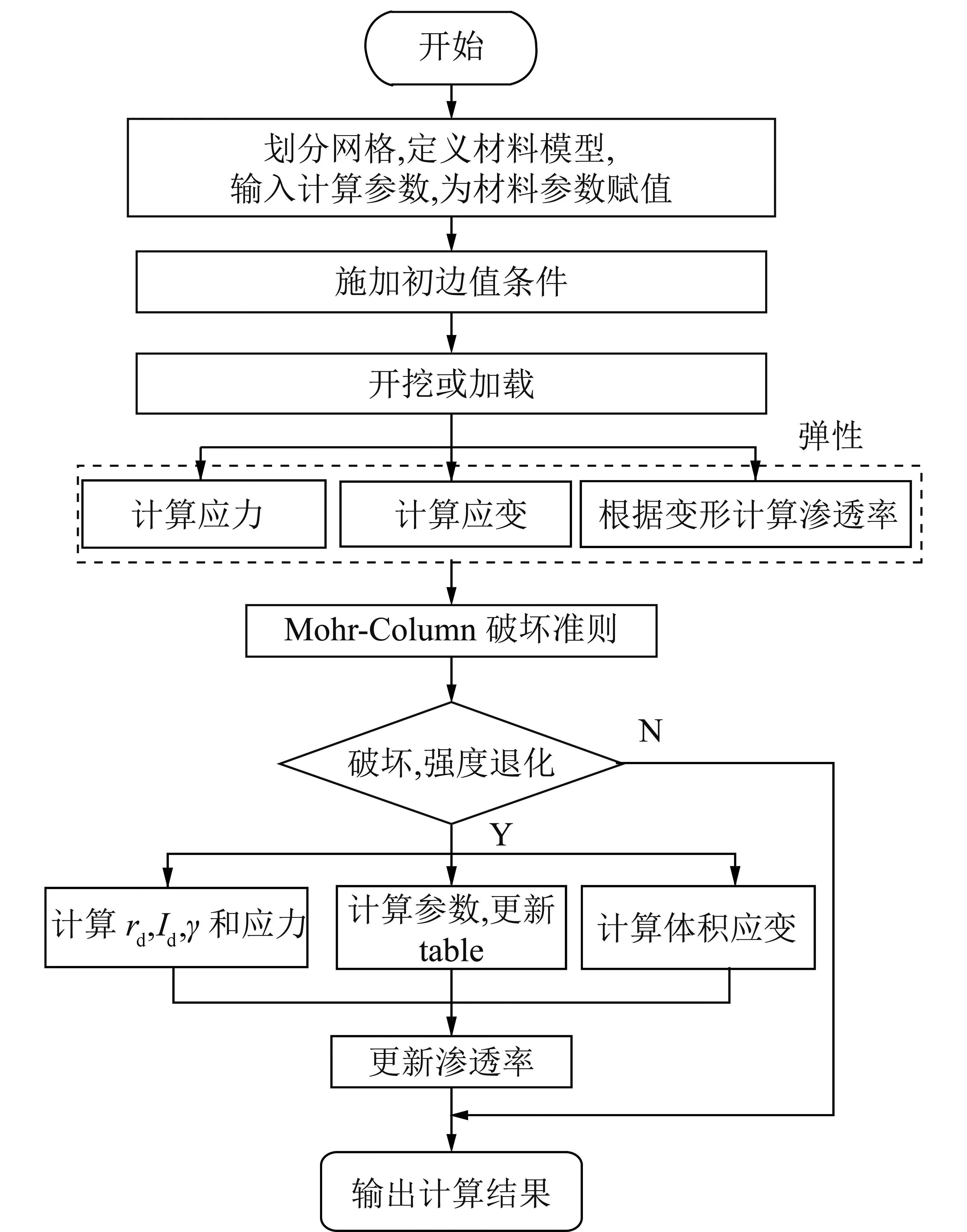
图5　本文模型实现过程Fig.5　Procedures for implementing the model in this paper

4模型验证

4.1Gebdykes白云岩三轴压缩模拟

文献[15]给出了Gebdykes白云岩三轴压缩实验数据，具体如图6所示。

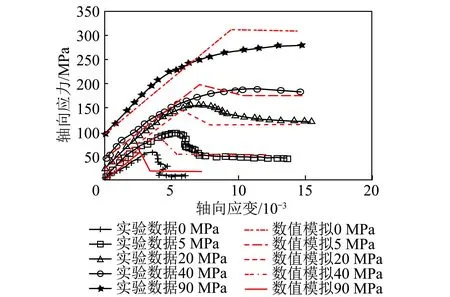
图6　Gebdykes白云岩三轴应力应变曲线Fig.6　Tri-axial stress-strain curves of Gebdykes dolomite

在FLAC下建立Gebdykes白云岩的三轴压缩数值模型，数值模型为圆柱形，尺寸为50 mm(直径) ×100 mm (高度)，在试样侧面施加围压0,5,20,40,90 MPa。轴向使用位移加载，速度为1.0×10-8m/step。数值模型中的物理力学参数见表2。残余内摩擦角和残余黏聚力由围压与残余强度数据通过拟合确定，由FLAC内编制的FISH函数自动完成。

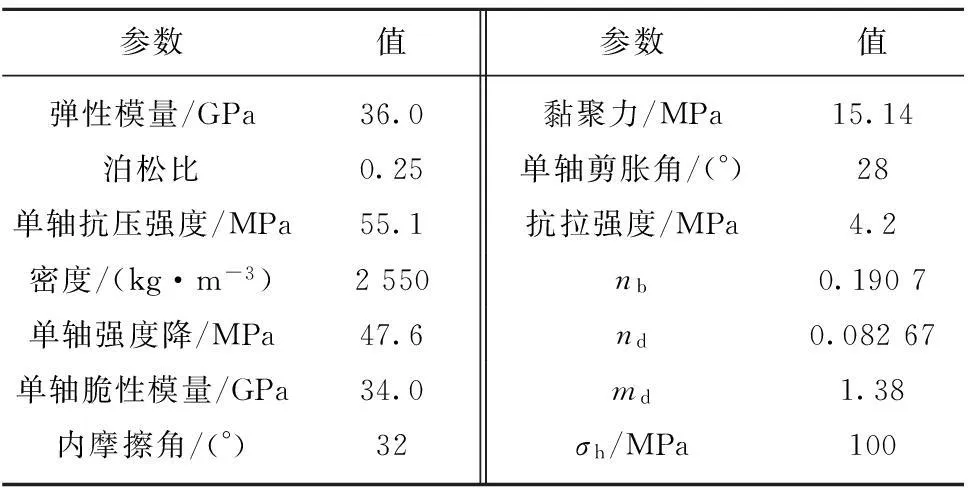
表2　Gebdykes白云石物理力学参数

利用数值模型模拟不同围压下Gebdykes白云岩压缩过程中轴向应力-轴向应变、体积应变-轴向应变曲线分别如图6和7所示。数值模拟结果与试验结果较为一致，本文模型能较好地描述三轴压缩岩样的峰后应变软化力学行为。

图7　Gebdykes白云岩体积应变-轴向应变曲线Fig.7　Curves of volumetric and axial strain of Gebdykes dolomite

从图6还可以看出，三轴压缩试验得到的岩石应力应变曲线呈非线性特征，本文模型将其简化为三段直线来研究是一种近似的简化研究，但数值模拟结果与试验结果相差不大，使用本文模型研究岩石的变形和破坏问题不致产生大的偏差。

4.2三轴压缩巴里坤砂岩的渗透率演化

取新疆巴里坤砂岩样开展了三轴压缩[5]和三轴稳态渗流实验[12]，获得了巴里坤砂岩的全程应力应变曲线和14 MPa围压下体积应变渗透率关系曲线。对14 MPa围压下体积应变渗透率关系曲线拟合，得到：

(18)

式(18)拟合结果与实验数据的相关系数为0.953，拟合效果好。

利用三轴应力应变曲线结合数据拟合，获得巴里坤砂岩物理力学参数见表3。

表3　巴里坤砂岩物理力学参数

在FLAC下建立数值模型，模型为圆柱形，尺寸为50 mm(直径) ×100 mm (高度)，在试样侧面施加围压0,6,14,26,40和50 MPa。轴向使用位移加载，速度为1.5×10-8m/step，模型中的物理力学参数见表3。

图8是本文模型数值模拟得到的渗透率与轴向应变关系曲线。从模拟结果可见，在整个压缩过程中，岩样的渗透率呈“V”型变化。在弹性压缩阶段，岩样孔隙空间压缩，渗透率降低；岩样破坏后，内部裂隙扩展和新裂隙萌生，岩样剪胀扩容，渗透率增长。围压对岩样的渗透率演化有很大影响，随着围压增加，岩样的剪胀扩容减缓，相应的渗透率增长也趋缓。

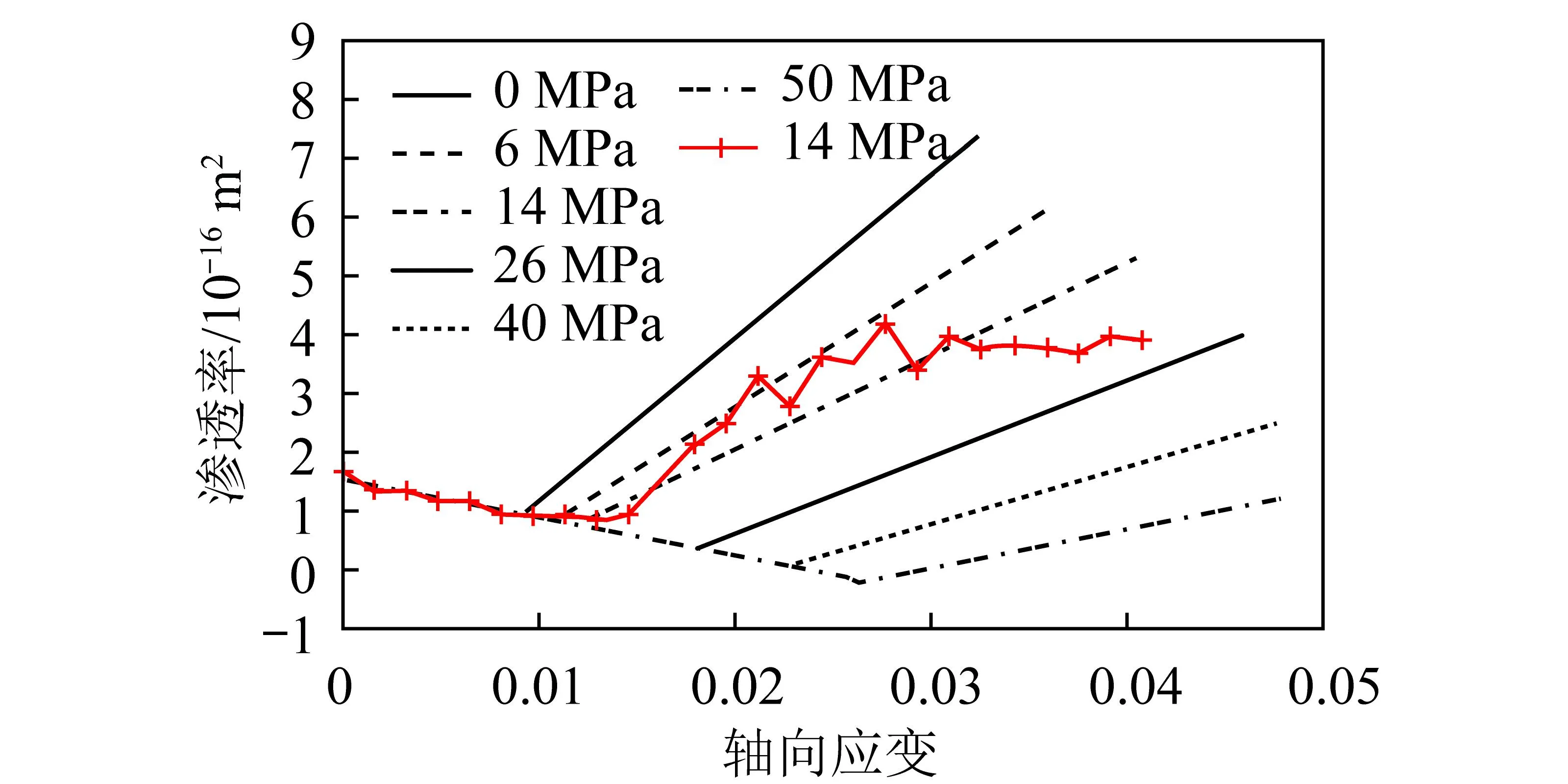
图8　不同围压下岩样的渗透率Fig.8　Permeability obtained from tests and numerical simulation under varied confining pressure

从图8可见，数值模拟的渗透率与实验结果基本一致，这表明本文模型是合理的，可以用于预测岩石工程中承载岩石的渗透率演化。

观察图8中渗透率的实验数据，发现在线弹性阶段岩样的渗透率减小，当应力达到峰值强度约2/3时，岩样渗透率的减小速率趋缓，甚至开始有缓慢增长。本文模型中假设岩石破坏时开始剪胀扩容，渗透率增长，从实验结果来看，由于峰前过渡段岩石的渗透率增加不大，因此本文的这一假定是合理的。

从图8的实验结果还可以发现，破坏后岩样的渗透率在稳定增长一段时间后，增长率快速趋缓。Zhao等[18]分析了这一现象，提出了动态剪胀角来描述岩石渗透率变化的这一特征。

从图6～8可以看出，数值模拟结果与试验结果还有一定偏差，这主要是数值计算中强度退化指数、脆性模量指数等的计算误差所致。

5模型应用

煤层开采过程中煤岩的渗透率演化规律预测是煤层瓦斯抽采和瓦斯灾害防治的关键，目前尚缺少好的定量分析方法[25]。这里尝试使用本文的岩石应变软化和渗透率演化模型模拟煤层开采过程中煤岩的渗透率动态演化规律。

本文算例的煤层厚度5.0 m，上覆岩层容重为26.5 kN/m3，赋存深度415 m，煤层倾向长185 m，走向长190 m。煤层竖向应力约为11 MPa，水平应力约为8 MPa，顶、底板为巴里坤砂岩。煤层回采75 m，分3步开采，第1步开采宽度30 m，第2步开采宽度30 m，第3步开采宽度15 m。数值计算模型的尺寸取为：煤层上方取75 m，下方取20 m，最终开采工作面两侧各取360 m，沿走向方面剖面计算，取平面应变模型。由于模型尺寸足够大，可以忽略边界条件对计算结果产生的影响。数值模型中单元尺寸为0.1 m×0.05 m。建立的数值模型示意如图9所示。

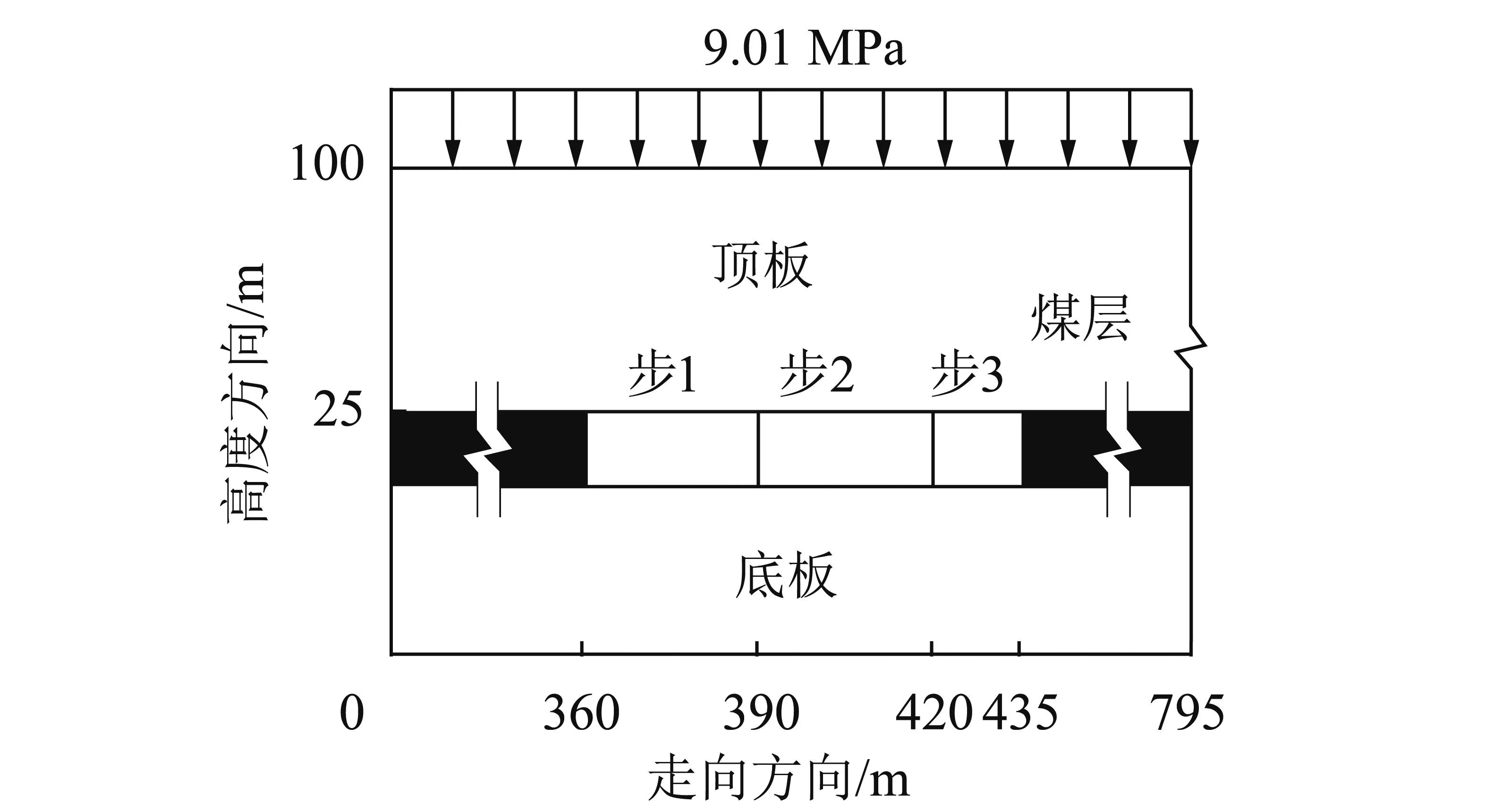
图9　煤层开采示意Fig.9　Sketch of coal excavation

煤的物理力学参数与巴里坤砂岩取相同。于是，数值模型中，顶、底板和煤的物理力学参数均按表3取值。

在顶板上方施加9.01 MPa的竖向压力模拟顶板上方的岩层重力，侧压系数为0.73，在计算中，首先形成岩层初应力，然后进行开采计算。

本文为平面应变模型，岩层单元的围压使用下式计算：

(19)

式中，σp,2，σp,3为单元的中主应力和小主应力。

图10为工作面推进过程中顶板煤岩的渗透率演化和分布情况。工作面开采前煤岩的初始渗透率1.756×10-16m2，当工作面开采后，采动煤岩应力重分布，一些区域压缩，煤岩的渗透率减小，另外一些区域煤岩发生拉伸变形或煤岩单元破坏，单元体体积扩容，渗透率增加。从图10可以看出，第1步开采后，在顶板上方5 m煤岩的渗透率平均约为2.4×10-16m2，相比采动前增加了36%。开采扰动使得顶板煤岩的渗透率增加，影响高度约21 m。随着第2步和第3步开采的进行，顶板煤岩的渗透率增加，影响高度也增加。当第2步开采后，顶板5 m范围内渗透率平均约为2.7×10-16m2，影响高度达到31 m。第3步开采后，顶板5 m范围内渗透率平均增加至3.0×10-16m2，影响高度达到33 m。

图10　工作面推进过程中顶板煤岩渗透率(10-16 m2)Fig.10　Permeability evolution of overburden rock over workface (10-16 m2)

图11为工作面推进过程中工作面前方渗透率分布情况。可见，第1步开采后，在开挖面前2 m内煤岩的渗透率平均为6.1×10-16m2，比开挖前增长了约2.5倍。在工作面前方2.5 m范围内煤岩的渗透率都有显著提高。随着接下来的开挖，开挖面前方煤岩渗透率继续增加，影响范围也进一步扩大。第2步开挖完成后，开挖面前方2 m范围内煤岩的渗透率平均为14.1×10-16m2，在前方3.8 m范围内渗透率都有显著增长。第3步开挖完成后，开挖面前方煤岩渗透率平均约为52.4×10-16m2，开挖面前方5.2 m范围内煤岩的渗透率都有显著增长。

图11　工作面推进过程中前方煤岩渗透率(10-16 m2)Fig.11　Permeability evolution of overburden rock before workface (10-16 m2)

从图10和11还可以发现，顶板及开挖面前方煤岩的渗透率等值线都呈“拱”形，渗透率从“拱”心向外逐渐减小。在煤层瓦斯抽采中，若将抽放孔布设于拱形圈内，将取得良好的抽采效果。

6结论

(1)脆性模量描述了岩石峰后强度跌落速度的快慢，脆性模量系数可以较好地描述围压对岩石峰后强度退化过程的影响。

(2)脆性模量系数方法主要适用于单轴应力应变曲线为I型的中硬和软岩，如砂岩、泥岩、大理岩等。

(3)本文模型能较好地模拟围压对岩石峰后应变软化和渗透率演化的影响。

(4)随着煤层开采，采动应力引起围岩变形、破坏，其渗透率也随之动态变化，本文模型能较好地再现煤层开采过程中围岩的渗透率动态演化规律。

参考文献:

[1]Hannah E Ross,Paul Hagin,Mark D Zoback.CO2storage and enhanced coalbed methane recovery:Reservoir characterization and fluid flow simulations of the Big George coal,Powder River Basin,Wyoming,USA[J].International Journal of Greenhouse Gas Control,2009,3:773-786.

[2]Yin G Z,Li W P,Jiang C B,et al.Mechanical property and permeability of raw coal containing methane under unloading confining pressure[J].International Journal of Mining Science and Technology,2013,23:789-793.

[3]Xue S,Yuan L,Xie J,et al.Advances in gas content based on outburst control technology in Huainan,China[J].International Journal of Mining Science and Technology,2014,24:385-389.

[4]Cai C,Li G,Huang Z,et al.Experimental study of the effect of liquid nitrogen cooling on rock pore structure[J].Journal of Natural Gas Science and Engineering,2014,21:507-517.

[5]张春会,赵全胜.饱水度对砂岩强度和模量影响的三轴试验[J].岩土力学,2014,35(4):951-958.

Zhang Chunhui,Zhao Quansheng.Triaxial tests of effects of varied saturations on strength and modulus for sandstone[J].Rock and Soil Mechanics,2014,35(4):951-958.

[6]杨圣奇,苏承东,徐卫亚.大理岩常规三轴压缩下强度和变形特性的试验研究[J].岩土力学,2005,26(3):475-478.

Yang Shengqi,Su Chengdong,Xu Weiya.Experimental investigation on strength and deformation properties of marble under conventional triaxial compression[J].Rock and Soil Mechanics,2005,26(3):475-478.

[7]苏承东,付义胜.红砂岩三轴压缩变形与强度特征的试验研究[J].岩石力学与工程学报,2014,33(S1):3164-3169.

Su Chengdong,Fu Yisheng.Experimental study of triaxial compression deformation and strength characteristics of red sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):3164-3169.

[8]杨永杰,宋扬,陈绍杰.三轴压缩煤岩强度及变形特征的试验研究[J].煤炭学报,2006,31(2):150-153.

Yang Yongjie,Song Yang,Chen Shaojie.Test study of coal’s strength and deformation characteristics under triaxial compression[J].Journal of China Coal Society,2006,31(2):150-153.

[9]Xin Tan,Heinz Konietzky,Thomas Frühwirt.Laboratory observation and numerical simulation of permeability evolution during progressive failure of brittle rocks[J].Int.J.Rock Mech.Min.Sci.,2014,68:167-176.

[10]于永江，张春会，赵全胜,等.承载围岩渗透率演化模型及数值分析[J].煤炭学报,2014,39(5):841-848.

Yu Yongjiang,Zhang Chunhui,Zhao Quansheng,et al.Permeability model for loaded rock and numerical analysis[J].Journal of China Coal Society,2014,39(5):841-848.

[11]Zhao X G,Cai M.A mobilized dilation angle model for rocks[J].Int.J.Rock Mech.Min.Sci.,2010,47:368-384.

[12]张春会,赵全胜,王来贵,等.三轴压缩岩石应变软化及渗透率演化的实验和数值模拟[J].煤炭学报,2015,40(8):1774-1782.

Zhang Chunhui,Zhao Quansheng,Wang Laigui,et al.Investigation of test and numerical modeling for strain softening behavior and permeability evolution of rock under tri-axial compression[J].Journal of China Coal Society,2015,40(8):1774-1782.

[13]Fang Z,Harrison J P.A mechanical degradation index for rock[J].Int.J.Rock Mech.Min.Sci.,2001,38:1193-1199.

[14]Fang Z,Harrison J P.Application of a local degradation model to the analysis of brittle fracture of laboratory scale rock specimens under triaxial conditions[J].Int.J.Rock Mech.Min.Sci.,2002,39:459-476.

[15]Yuan S C,Harrison J P.An empirical dilatancy index for the dilatant deformation of rock[J].Int.J.Rock Mech.Min.Sci.,2004,41:679-686.

[16]Yuan S C,Harrison J P.Development of a hydro-mechanical local degradation approach and its application to modelling fluid flow during progressive fracturing of heterogeneous rocks[J].Int.J.Rock Mech.Min.Sci.,2005,42:961-984.

[17]薛东杰,周宏伟,唐咸力,等.采动煤岩体瓦斯渗透率分布规律与演化过程[J].煤炭学报,2013,38(6):930-935.

Xue Dongjie,Zhou Hongwei,Tang Xianli,et al.Evolution of mining-induced enhancement and distribution of gas permeability in coal seam and surrounding rock[J].Journal of China Coal Society,2013,38(6):930-935.

[18]Cai Y D,Liu D M,Jonathan P Mathews,et al.Permeability evolution in fractured coal Combining tri-axial confinement with X-ray computed tomography,acoustic emission and ultrasonic techniques[J].International Journal of Coal Geology,2014,122:91-104.

[19]Chen Y F,Hu S H,Wei K,et al.Experimental characterization and micromechanical modeling of damage-induced permeability variation in Beishan granite[J].International Journal of Rock Mechanics & Mining Sciences,2014,71:64-76.

[20]谢和平,高峰,周宏伟,等.煤与瓦斯共采中煤层增透率理论与模型研究[J].煤炭学报,2013,38(7):1101-1108.

Xie Heping,Gao Feng,Zhou Hongwei,et al.On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas[J].Journal of China Coal Society,2013,38(7):1101-1108.

[21]Tang C A,Liu H,Lee P K K,et al.Numerical studies of the influence of microstructure on rock failure in uniaxial compression-Part I:Effect of heterogeneity[J].Int.J.Rock Mech.Min.Sci.,2000,37:555-569.

[22]蔡朋,邬爱清,汪斌,等.一种基于II型全过程曲线的岩爆倾向性指标[J].岩石力学与工程学报,2010,29(S1):3290-3294.

Cai Peng,Wu Aiqing,Wang Bin,et al.A rockburst proneness index based on class II whole process curve[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):3290-3294.

[23]ITASCA.Fast Lagrangian Analysis of Continua,Version 5.0,Minnesota,2012.

[24]Zhang Chunhui,Wang Laigui,Du Jianhua,et al.Numerical modelling rock deformation subject to nitrogen cooling to study permeability evolution[J].Int.J.Coal Sci.Technol,2015,DOI:10.1007/s40789-015-0084-z.

[25]张春会,赵莺菲,王来贵,等.采动煤岩渗透率演化模型及数值模拟[J].岩土力学,2015,36(8):2409-2418.

Zhang Chunhui,Zhao Yingfei,Wang Laigui,et al.Permeability evolution model of mined coal rock and its numerical simulation[J].Rock and Soil Mechanics,2015,36(8):2409-2418.

Strain softening and permeability evolution model based on brittle modulus coefficient

ZHANG Chun-hui1,2,YUE Hong-liang1,WANG Lai-gui2,GUO Xiao-kang1,YU Yong-jiang2

(1.SchoolofCivilEngineering,HebeiUniversityofScienceandTechnology,Shijiazhuang050018,China;2.SchoolofMechanicsScienceandEngineering,LiaoningTechnicalUniversity,Fuxin123000,China)

Abstract:The scientific predictions of the strain softening and permeability evolution behaviors of rock are the basis of the stability and safety analysis in rock engineering.Through the analysis on the tri-axial compression tests data,the laws of the effects of confining pressure on the strain softening mechanical behaviors of rock are presented.To describe the effects of the confinement on the brittleness of peak-post rock,the brittle modulus and the brittle modulus coefficient are proposed.The physical meanings of the brittle modulus and the application scope of the brittle modulus coefficient are also described.Adopting the brittle modulus coefficient,combined with the strength degradation index,dilatancy index,SS model in FLAC and the method of the enhanced permeability of volumetric strain,a new strain softening and permeability evolution model has been developed.Using FLAC software,the deformation and permeability evolution behaviors under the different confining pressures of Gebdykes dolomite and Balikun sandstone are better numerically modeled,and the model proposed in this paper is proved to be valid.Lastly the model proposed in this paper is used to predict the permeability dynamic evolution of overburden rock due to mining.The results show with the work face advance the deformations and failures of overburden rock appear due to mining disturbance stresses,and correspondingly the permeability of rock dynamically changes.The process is better numerically modeled by the model proposed in this paper.

Key words:Brittle modulus coefficient;the enhanced permeability of the volumetric strain;permeability evolution;strain softening

中图分类号:TD315

文献标志码:A

文章编号:0253-9993(2016)1-0255-10

作者简介:张春会(1976—)，男，辽宁阜新人，教授，博士。Tel:0311-81668904,E-mail:zhangchunhui789@126.com。通讯作者：岳宏亮(1980—)，男，河北石家庄人，讲师，硕士。Tel:0311-81668904,E-mail:yuehongliang2000@126.com

基金项目:国家自然科学基金资助项目(51274079,51574139,51274110)

收稿日期:2015-06-05修回日期:2015-10-13责任编辑:常琛

张春会,岳宏亮,王来贵,等.基于脆性模量系数的岩石应变软化及渗透率演化模型[J].煤炭学报,2016,41(1):255-264.doi:10.13225/j.cnki.jccs.2015.0833

Zhang Chunhui,Yue Hongliang,Wang Laigui,et al.Strain softening and permeability evolution model based on brittle modulus coefficient[J].Journal of China Coal Society,2016,41(1):255-264.doi:10.13225/j.cnki.jccs.2015.0833