EXISTENCE AND UNIQUENESS OF GLOBAL SOLUTIONS OF THE MODIFIED KS-CGL EQUATIONS FOR FLAMES GOVERNED BY A SEQUENTIAL REACTION∗

Boling Guo

(Institute of Applied Physics and Computational Mathematics,Beijing,100088,P.R.of China)

Binqiang Xie

(The Graduate School of China Academy of Engineering Physics, P.O.Box 2101,Beijing,100088,P.R.of China)

EXISTENCE AND UNIQUENESS OF GLOBAL SOLUTIONS OF THE MODIFIED KS-CGL EQUATIONS FOR FLAMES GOVERNED BY A SEQUENTIAL REACTION∗

Boling Guo†

(Institute of Applied Physics and Computational Mathematics,Beijing,100088,P.R.of China)

Binqiang Xie

(The Graduate School of China Academy of Engineering Physics, P.O.Box 2101,Beijing,100088,P.R.of China)

In this paper,we are concerned with the existence and uniqueness of global solutions of the modified KS-CGL equations for flames governed by a sequential reaction,where the term|P|2Pis replaced with the generalized form|P|2σP, see[18].The main novelty compared with[18]in this paper is to control the norms of the f i rst order of the solutions and extend the global well-posedness to three dimensional space.

existence and uniqueness;modified KS-CGL;global solutions

2000 Mathematics Subject Classification 76E25;76E17;76W05; 35Q35

1 Introduction

This paper is devoted to the existence and uniqueness of global solutions of the following coupled modified Kuramoto-Sivashinsky-complex Ginzburg-Landau(GKSCGL)equations for flames

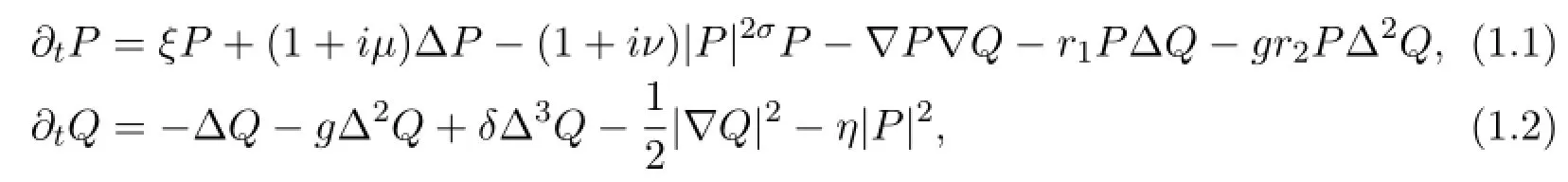
with the periodic initial conditions

where Ω is a box with lengthLdenotedTn(n=1,2,3).The complex functionP(x,t)denotes the rescaled amplitude of the flame oscillations,and the real functionQ(x,t)is the deformation of the f i rst front.The Landau coefficientsµ,νand the coupling coefficientη＞0 are real,whiler1andr2are complex parameters of the formr1=r1r+ir1i,r2=r2r+ir2i,respectively.The coefficientg＞0 is proportional to the supercriticality of the oscillatory mode,δ＞0 is a constant,L＞0 is the period andeiis the standard coordinate vector,and the coefficientξ=±1.The parameterσ,µ,νsatisfy

Forδ=0,the coupled GKS-CGL equations(1.1)and(1.2)are reduced to the classical KS-CGL equations[1],which describe the nonlinear interaction between the monotonic and oscillatory modes of instability of the two uniformly propagating flame fronts in a sequential reaction.Specifically,they describe both the long-wave evolution of the oscillatory mode near the oscillatory instability threshold and the evolution of the monotonic mode.For the background of the uniformly propagating premixed flame fronts and the derivation of the KS-CGL model,one refer to[1-4] for details.If there exist no coupling with the monotonic model,then equation(1.1) is the well-known CGL equation that describes the weakly nonlinear evolution of a long-scaled instability[5].Forδ=0 and the coupled coefficientη=0 in equation (1.2),equation(1.2)reduces to the well known KS equation[6],which governs the flame front’s spatio-temporal evolution and produces monotonic instability.It’s seen that the coupled GKS-CGL equations(1.1)and(1.2)can better describe the dynamical behavior for flames governed by a sequential reaction,since they generalize the KS equations,the CGL equations,and the KS-CGL equations.

So far,the mathematical analysis and physical study about the CGL equation and KS equation have been done by many researchers.For example,the existence of global solutions and the attractor for the CGL equation were studied in[7-11]. For some other results,see[12-15]and reference therein.However,little progress has been made for the coupled KS-CGL equations which are derived to describe the nonlinear evolution for flames by A.A.Golovin,eta[1],who studied the traveling waves of the coupled equations numerically and the spiral waves in[16],where new types of instabilities are exhibited.Meanwhile,there are few works to consider mathematical analytical properties of the KS-CGL equations and the generalized KS-CGL equations,even the existence and uniqueness of the solutions.

In[17],the Littlewood-Paley theory is used to obtain the local solution and global solution with small initial conditions for the coupled KS-Burgers which are derived by[1],while in[18]an additional sixth order term is added to control the nonlinear term estimate through which one can get the global smooth solution of the generalized GKS-CGL equation.In this paper,via delicate a prior estimates and the Galerkin method,we consider the global smooth solution of GKS-CGL equations where the third term is replaced by(1+iν)|P|2σP,that is,we study system(1.1)-(1.4)and extend the global well-posedness to the three dimensional space.

The rest of this paper is organized as follows.In Section 2,we brief l y give some notations and preliminaries.In Section 3,local solutions are constructed by the contraction mapping theorem.A prior estimates for the solutions of the periodic initial value problem(1.1)-(1.4)are obtained in Section 4.In Section 5,we deduce from the so-called continuity method that the existence and uniqueness of the global solutions of the periodic initial value problem(1.1)-(1.4).

2 Notaions and Preliminaries

For convenience,we will recall some notations and preliminaries which will be used in the sequel.

Letand(k=1,2,···)denote the Sobolev spaces ofL-periodic and complex-valued functions respectively endowed with norms

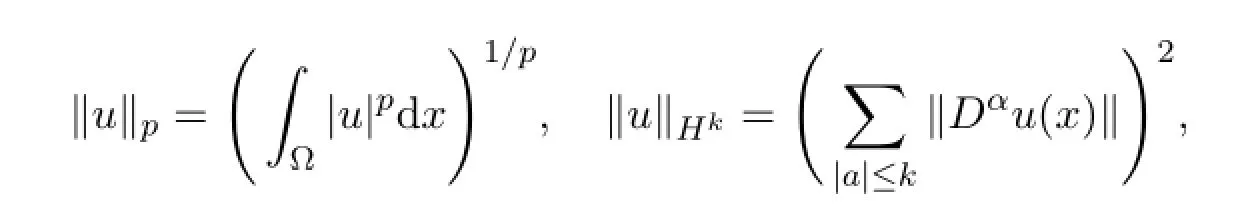
Now,we give some useful inequalities.

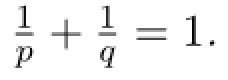
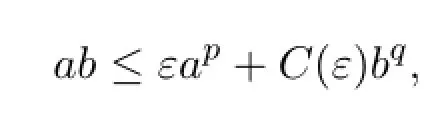
for C(ε)=(εp)-q/pq-1.

Lemma 2.2[20](Gagliardo-Nirenberg inequality)LetΩbe a bounded domain with∂Ωin Cm,and u be any function in Wm,r∩Lq(Ω),1≤q,r≤∞.For any integer j,0≤j＜m and for any number a in the interval j/m≤a≤1,set

If m-j-n/r is not nonnegative integer,then

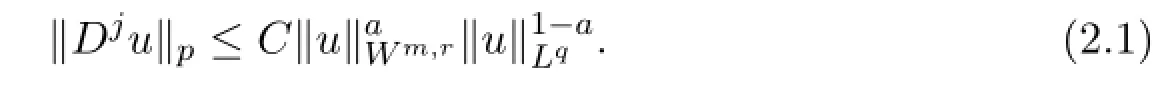
If m-j-n/r is a nonnegative integer,then(2.1)holds for a=j/m.The constant C depends only onΩ,r,q,j and a.

In the sequel,we will use the following inequalities which are the specif i c cases of the Gagliardo-Nirenberg inequality:

3 Local Solution

In this section,we will use the contraction mapping principle to prove the local solution of system(1.1)-(1.4).

For convenience,we rewrite the system as an abstract form

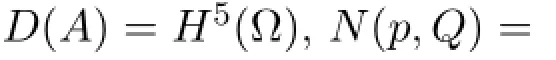
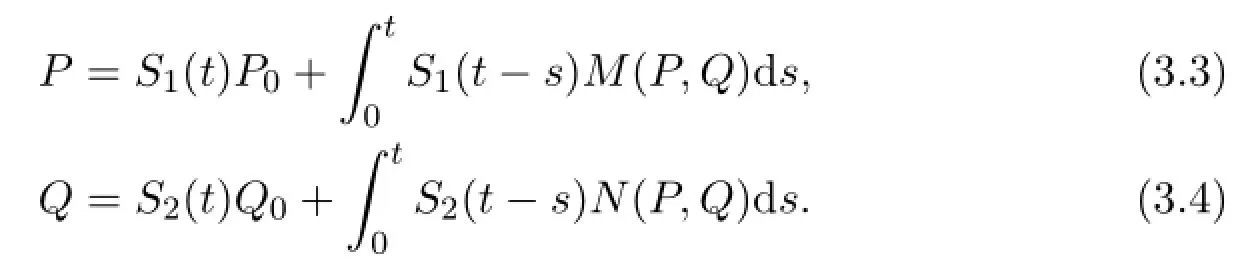
Then,def i ne a mapping

where

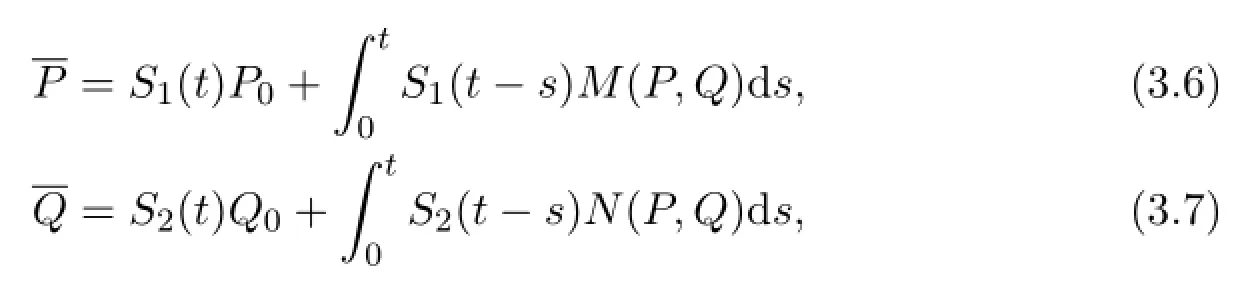
and def i ne a normed linear space

therefore,

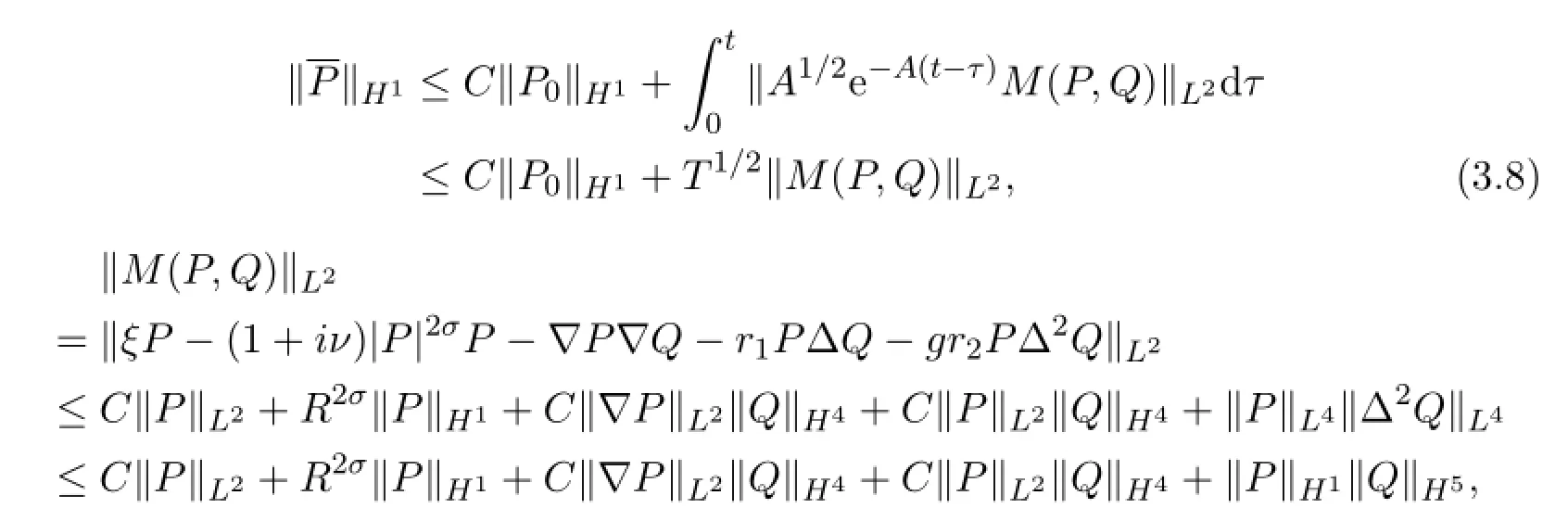
here the Sobolev imbedding theoremH1,→L2(2σ+1)is used,then we obtain

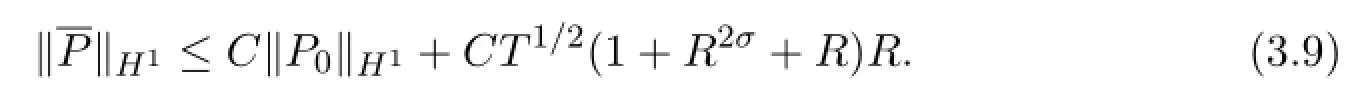
Therefore,whenTis small,ℜmapsℑinto itself.Similarly,we get

then we have

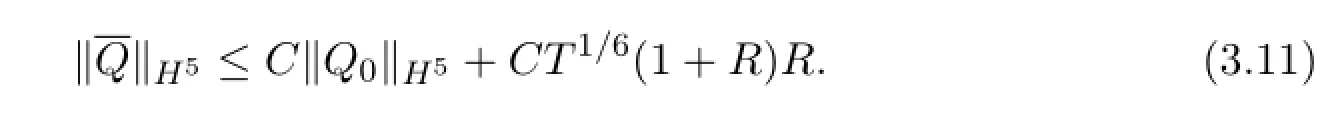
Therefore,whenTis small,ℜmapsℑinto itself.

Now,we proveℜis a contractive mapping onℑ,since

where

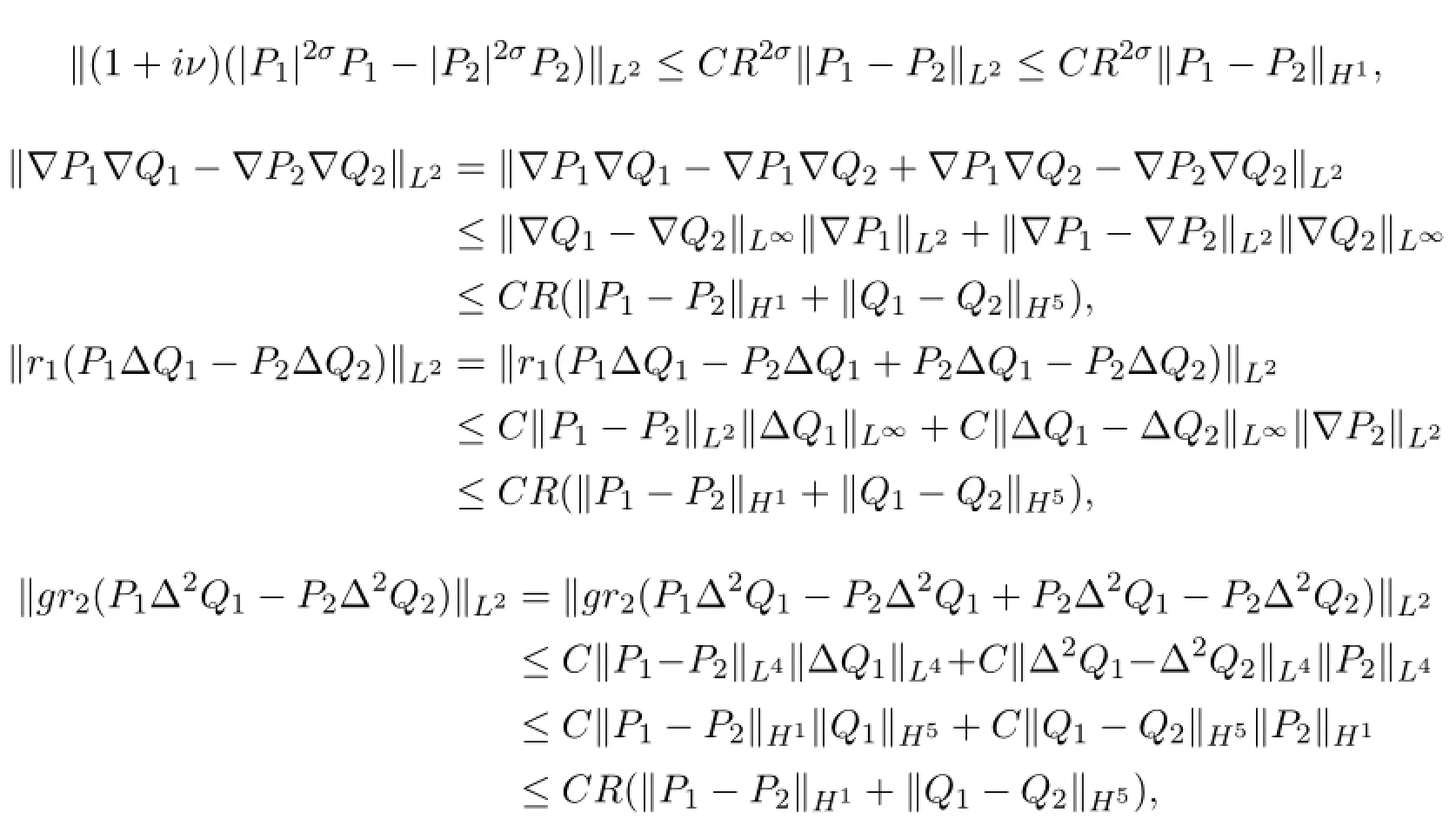
then we have

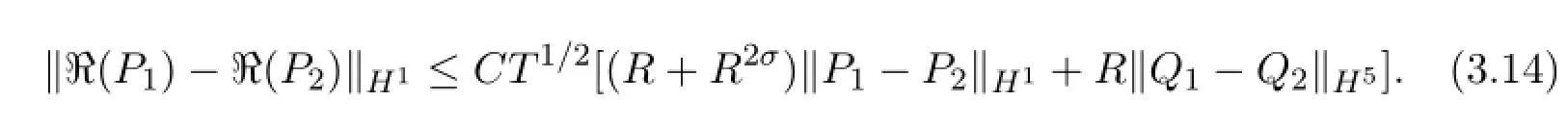
Similarly,we get

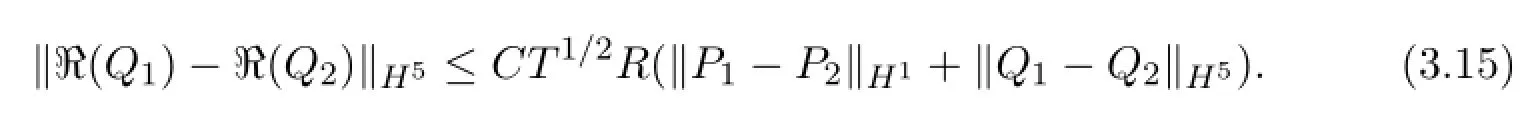
Adding the above two inequalities,we f i nally deduce

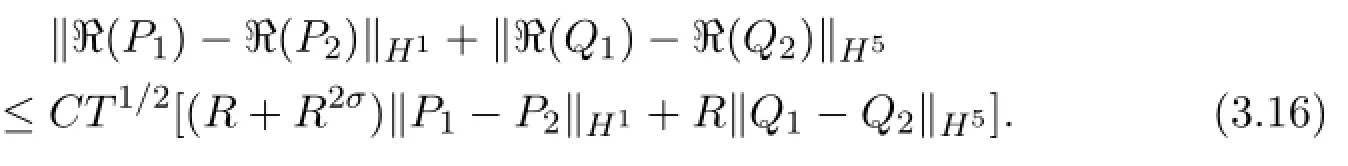
whereTdepends on‖P0‖H1(Ω)and‖Q0‖H5(Ω).

4 A Priori Estimates

In this section,we will derive the a priori estimates for the solutions of problem (1.1)-(1.4).Firstly,we have:

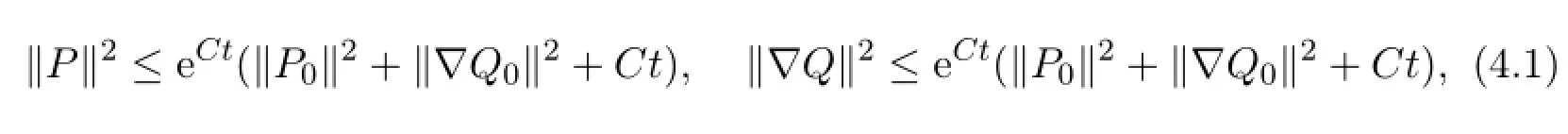
for C is a positive constant.

Proof Firstly we dif f erentiate equation(1.2)with respect toxonce and set

then equations(1.1)and(1.2)can be rewritten as

Multiplying(4.3)by,integrating with respect toxover Ω and taking the real part,we obtain

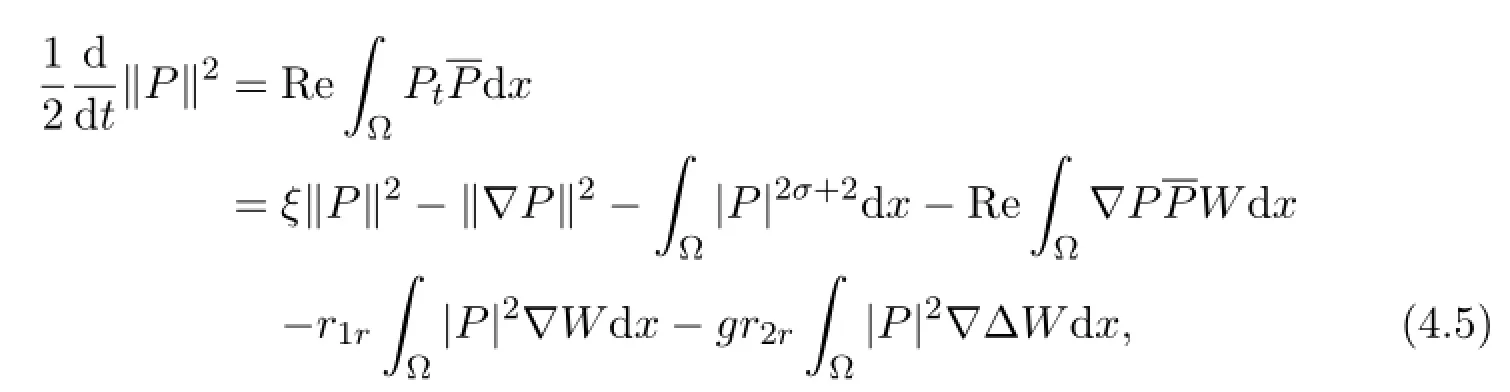
where

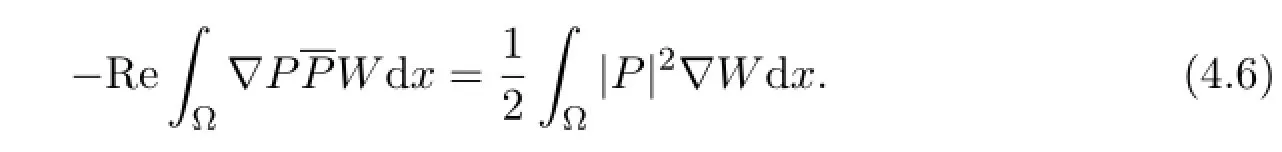
On the other hand,multiplying(4.4)byWand integrating over Ω,we have

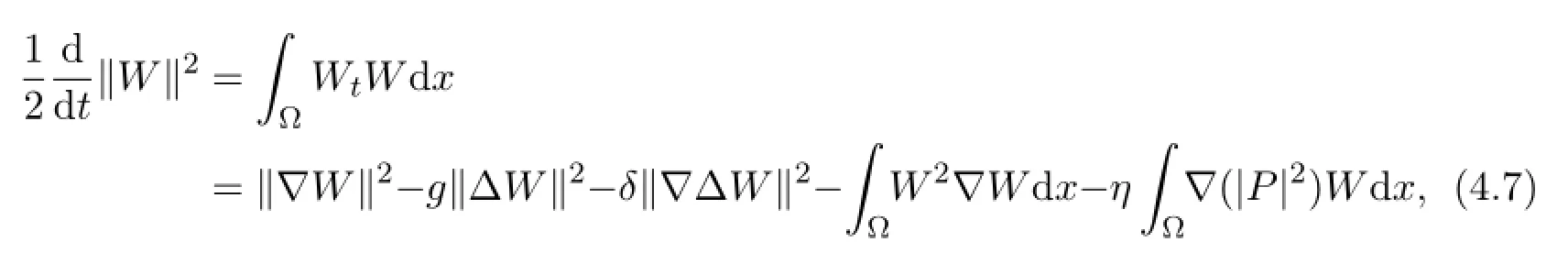
where

and

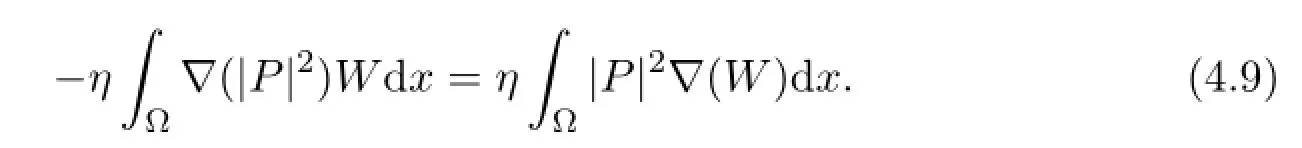
Adding(4.5)and(4.7)together,and noticing(4.6),(4.8)and(4.9),we deduce

According to Young’s inequality(2.2)and H¨older’s inequality,we have

and

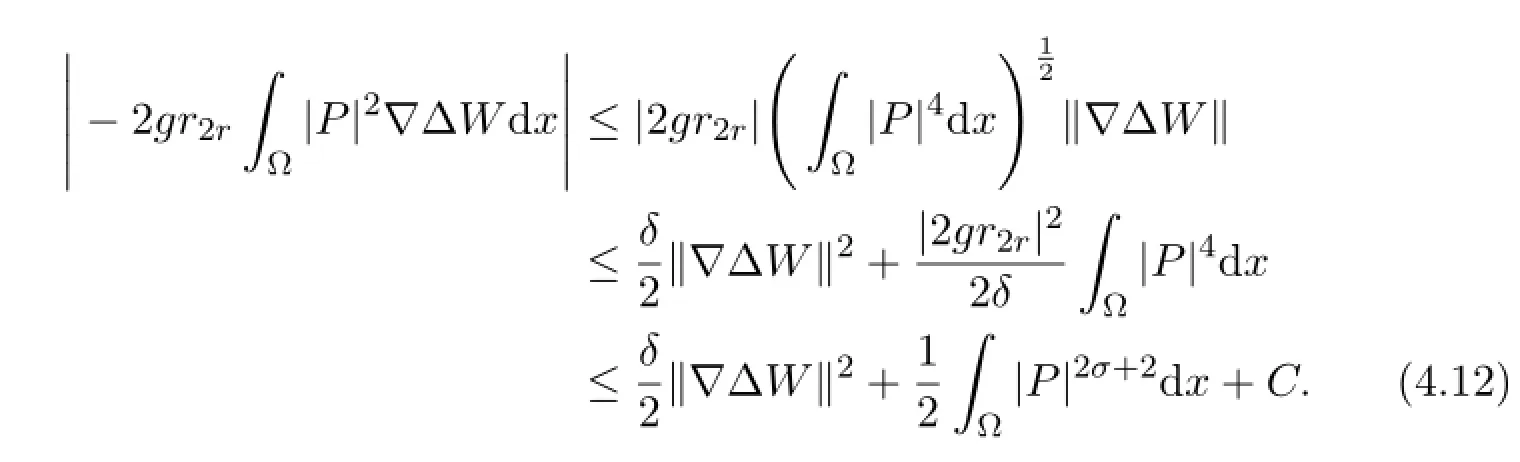
Combining(4.10)-(4.12)and|ξ|=1,we have

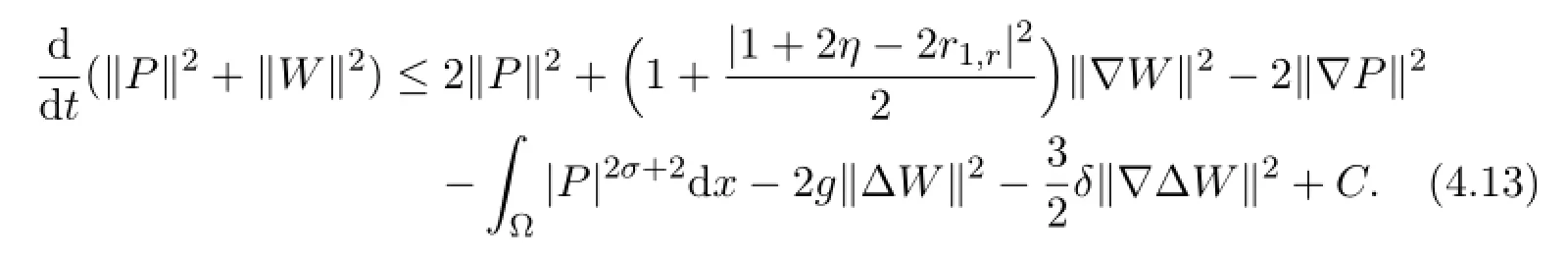
Using Gagliardo-Nirenberg inequality(2.3),we deduce

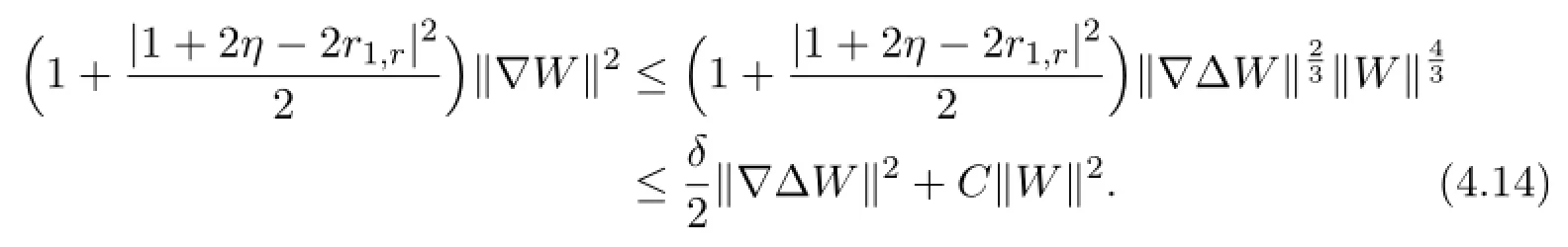
By(4.13)and(4.14),we obtain

then we deduce from Gronwall’s inequality that

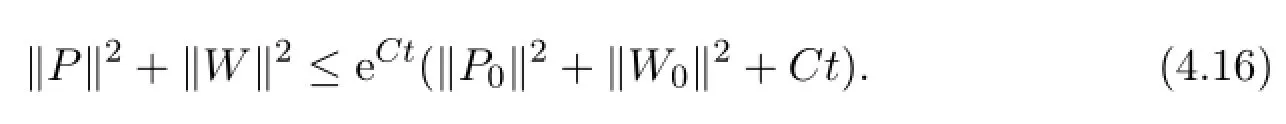
Lemma 4.2Under the assumptions of Lemma3.1,we have

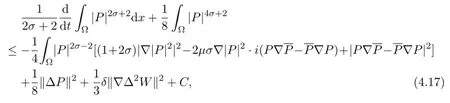
where C is a positive constant.

Proof Since

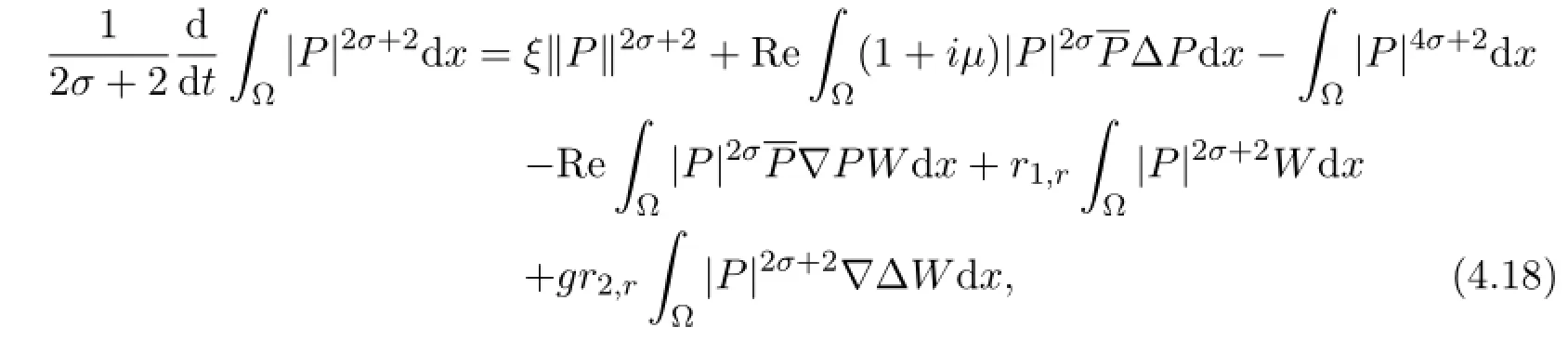
for the second term of RSH of(4.18),we have

for the remaining four terms,using Young’s and Gagliargo-Nirenberg inequalities, we have

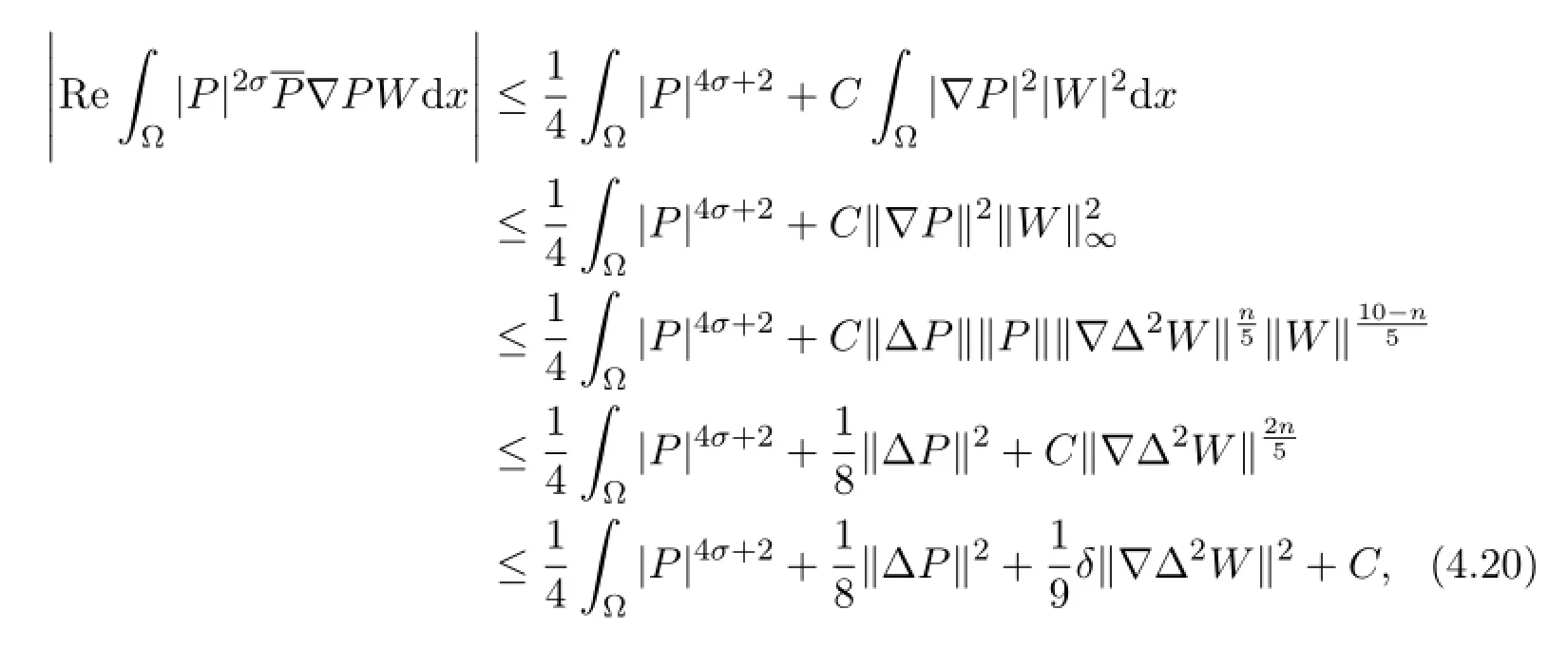
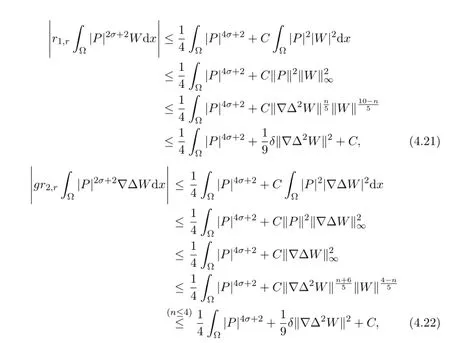
and

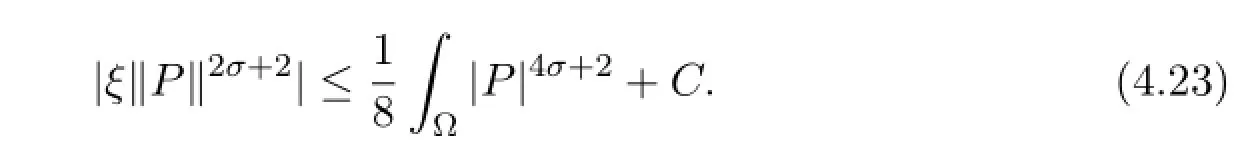
Combing the above estimates,we complete the proof.

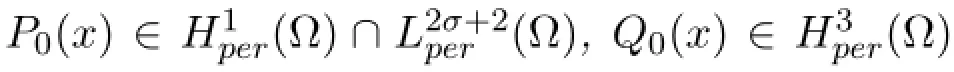
where C is a positive constant.

ProofMultiplying(4.3)by,integrating with respect toxover Ω and taking the real part,we obtain

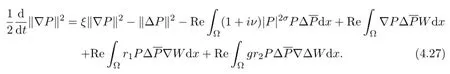
Multiplying(4.4)by-∆Wand-∆2W,and integrating over Ω respectively,we deduce

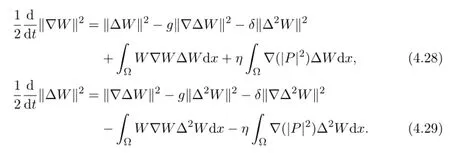
Adding(4.27),(4.28)and(4.29),we get

Now we need to control the right hand side of(4.30).Firstly,for the seventh term, we obtain

Meanwhile,according to Young’inequality and Gagliardo-Nirenberg inequality,we obtain the following estimates

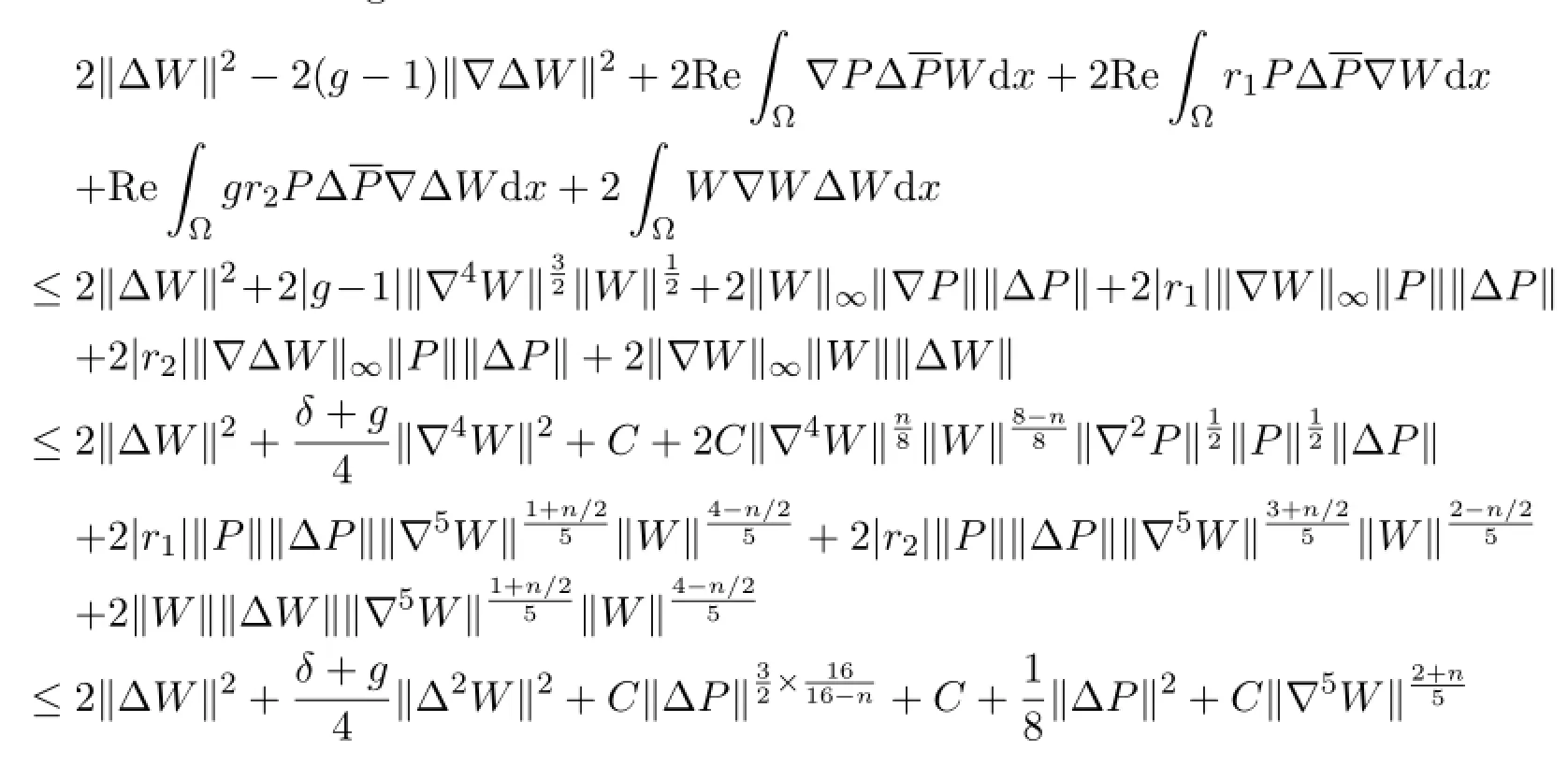
Next,for the remaining two terms,we obtain

and

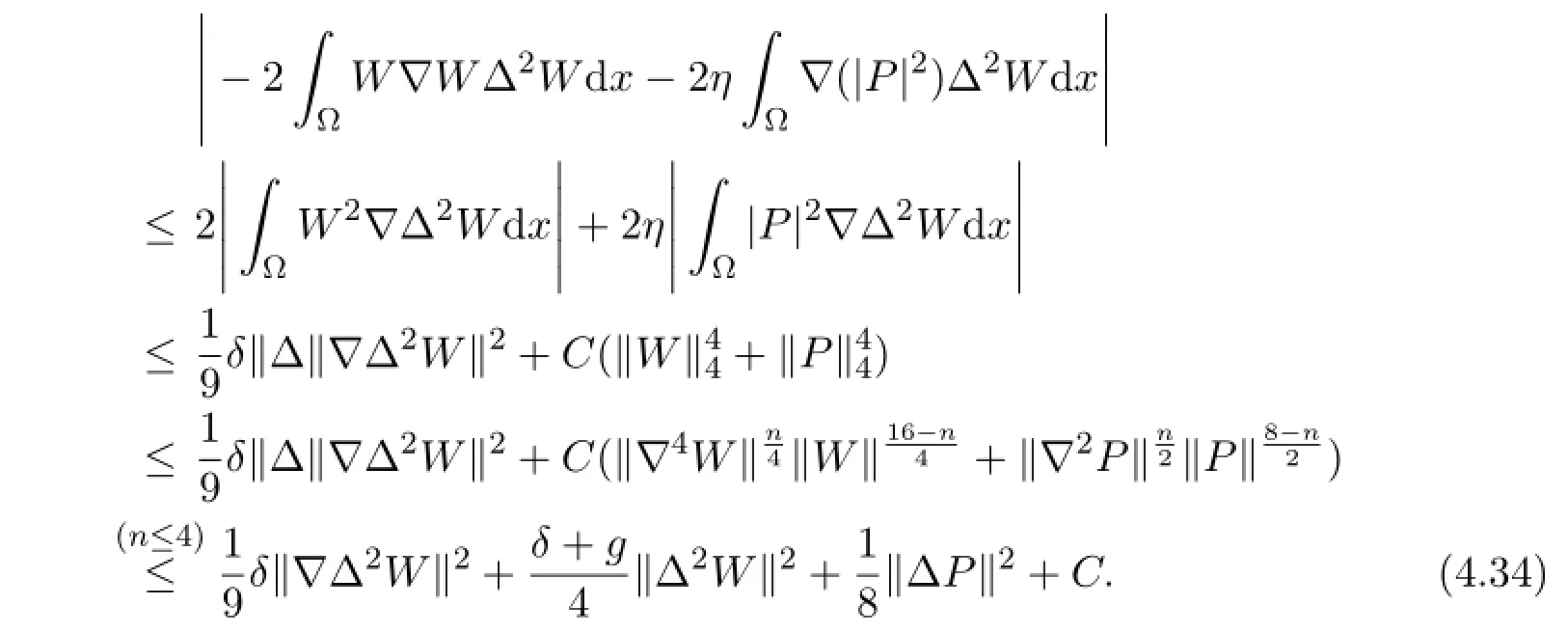
Combing the above estimates,we have

Adding(4.17)and(4.35),we have

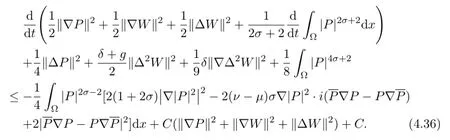
The following lemma was proved in[18],we omit the proof here.

Lemma 4.4Under the assumptions of Lemma3.3,we have

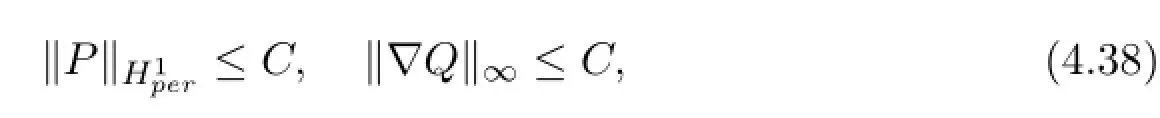
where C is a positive constant.

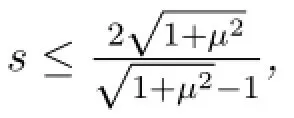
where C is a positive constant.

Proof By replacing the exponentσ+2 in Lemma 4.2 bys,we have

Lemma 4.6Let P0(x)(Ω),Q0(x)(Ω)and suppose that σ＞1andΩis a bounded domain with∂Ωin Cm.Then

where C is a positive constant.

Multiplying(4.4)by-∆3Wand integrating over Ω,we deduce

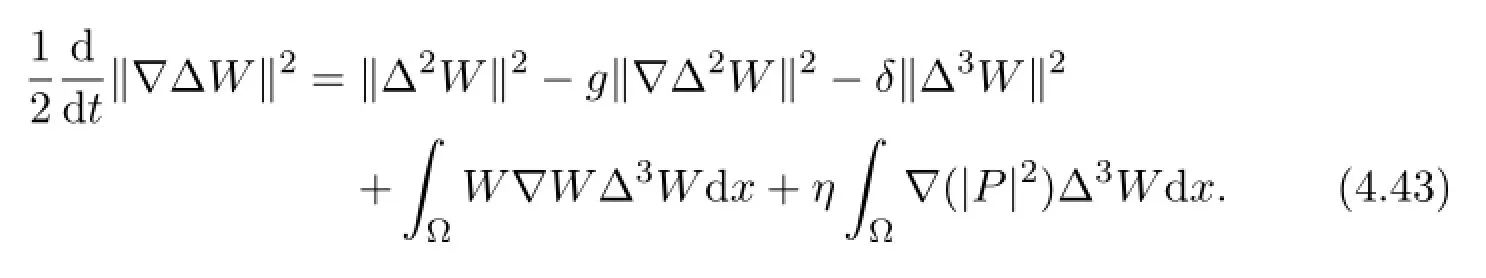
Adding the above two equalities yields

According to Gagliardo-Nirenberg inequality,Lemmas 4.1,4.3 and 4.5 and assumption(A2),we have

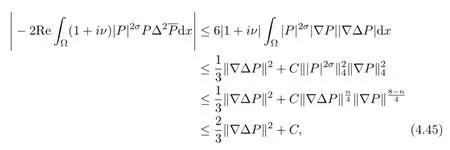
and

For the remaining terms of the RHS of(4.44),we have

and

Then combining(4.44)-(4.48)and noticing|ξ|=1,we have

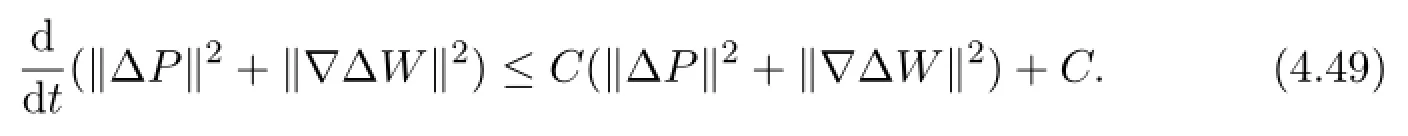
Lemma 4.7Let P0(x)(Ω),Q0(x)(Ω)and suppose that σ＞1andΩis a bounded domain with∂Ωin Cm.Then

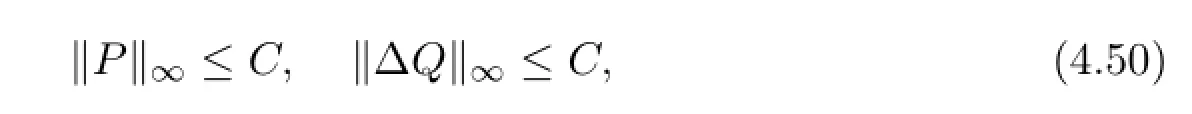
where C is a positive constant.

Lemma 4.8Let P0(x)(Ω),Q0(x)(Ω)and suppose that σ＞1be a bounded domain with∂Ωin Cm.Then

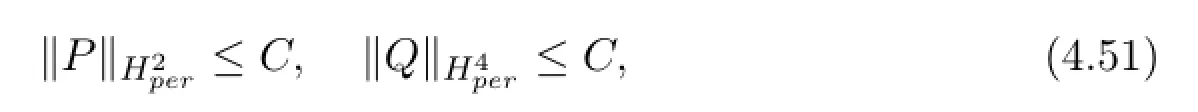
for C is a positive constant.

For the proof of Lemmas 4.7 and 4.8 in detail,one can refer to[18].

Lemma 4.9Let P0(x)(Ω),Q0(x)(Ω)and suppose that σ＞1andΩis a bounded domain with∂Ωin Cm.Then

where C is a positive constant.

Proof Multiplying(4.3)by,integrating over Ω and taking the real part, we obtain

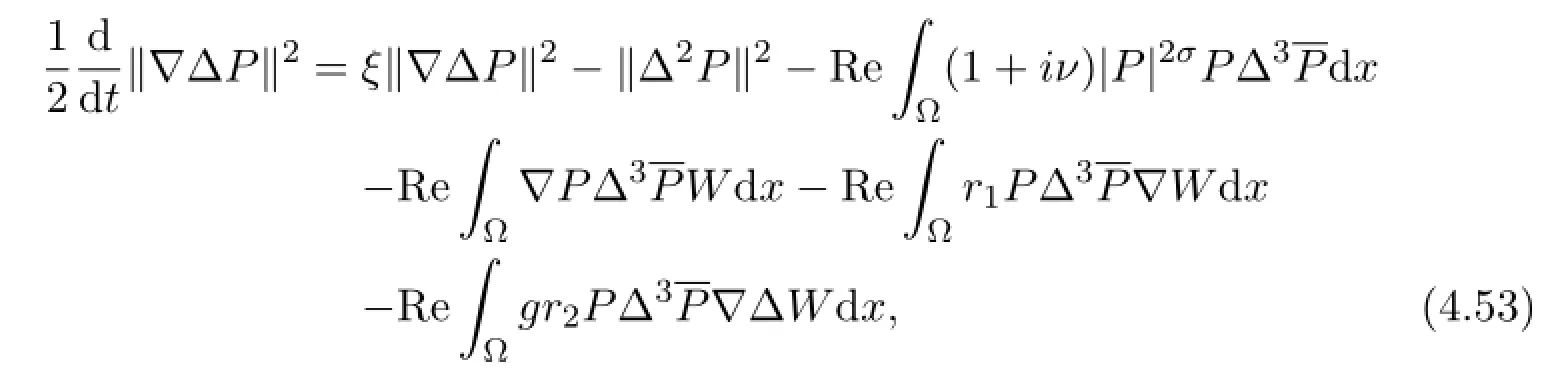
Multiplying(4.4)by∆4Wand integrating over Ω,we deduce

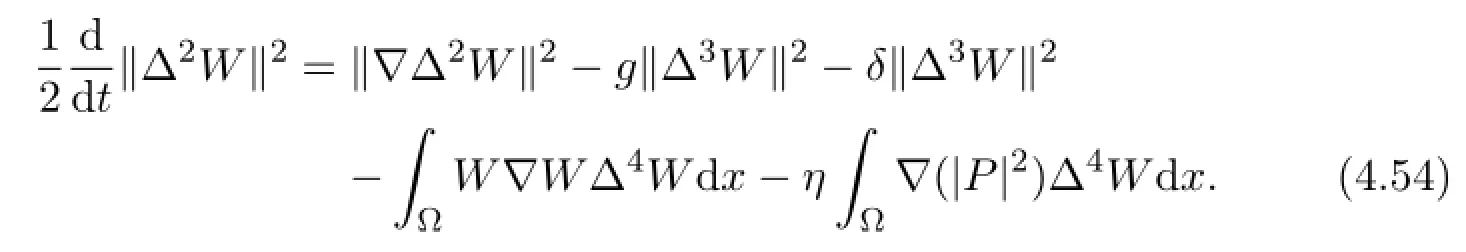
Adding the above two equalities arrives at

In order to control the RHS of(4.44),using the previous lemmas,we have

and

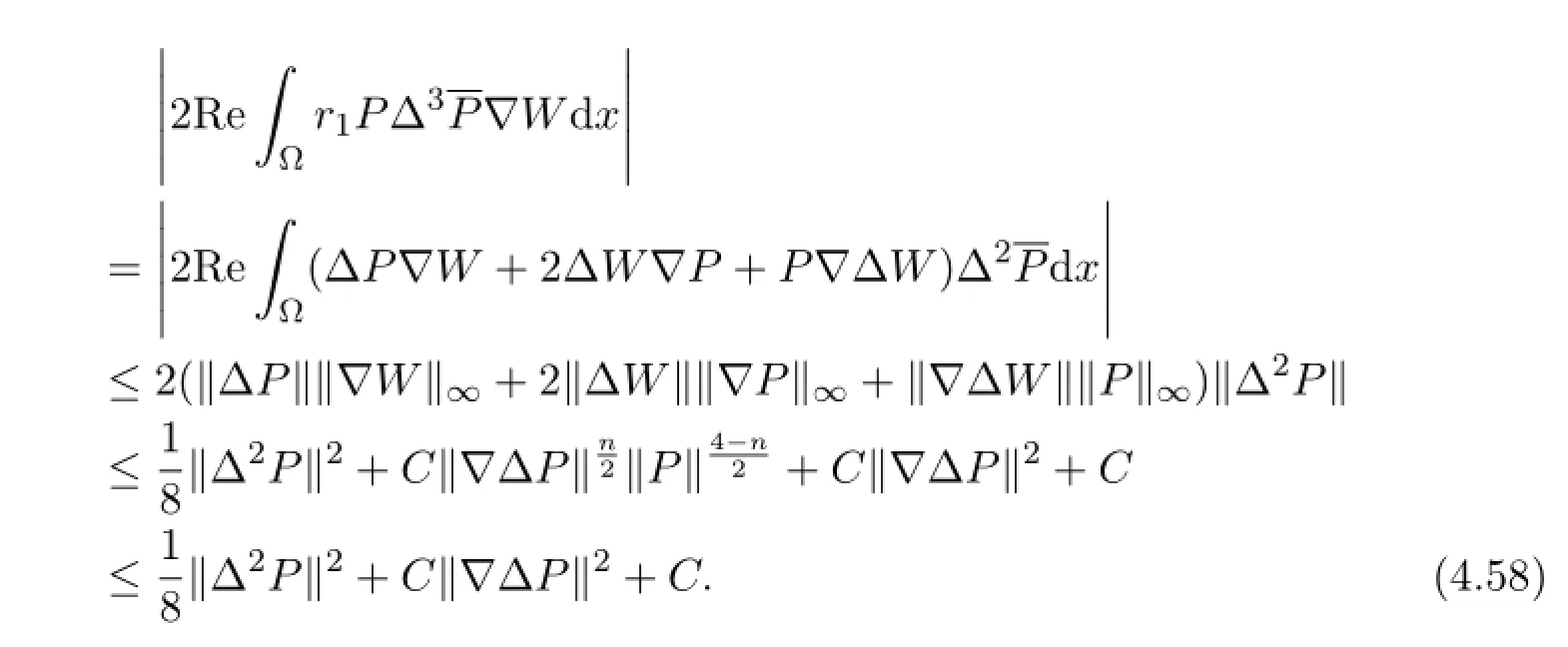
For the remaining terms,using Gagliardo-Nirenberg inequality and the previous estimates,we obtain

Combing the above estimates yields that

Therefore,from the above lemmas,we get the following lemma.

Lemma 4.10Let P0(x)(Ω),Q0(x)(Ω)and suppose that σ＞1andΩis a bounded domain with∂Ωin Cm.Then

where C is a positive constant.

5 The Local Solutions and Global Solutions

In this section,we will obtain the existence and uniqueness of the local solutions and global solutions of the periodic initial value problem(1.1)-(1.4).From the lemmas in Section 3,we deduce our main result:

Theorem 5.1(Local existence)Assume that P0(x)(Ω),Q0(x)(Ω)and the parameter σ,µ,ν satisfy assumptions(A1)and(A2).Then there exist local solutions P(x,t)and Q(x,t)to the periodic initial value problem(1.1)-(1.4),satisfying

where t0

Finally,we are able to deduce from this local existence theorem combined with the a priori estimates that the solutions exist globally in time.

Theorem 5.2(Global existence)Assume that P0(x)(Ω),Q0(x)(Ω)and the parameter σ,µ,ν satisfy assumptions(A1)and(A2).Then there exist global solutions P(x,t)and Q(x,t)to the periodic initial value problem(1.1)-(1.4),satisfying

where the periodic initial value problem(1.1)-(1.4).

Proof From Theorem 5.1,there exist local solutionsP(x,t)andQ(x,t)of the periodic initial value problem(1.1)-(1.4)and the existence timet0depends on‖P0(x)and‖Q0(x).According to the priori estimates in Section 4 and the so-called continuity method,we complete the proof.

[1]A.Golovin,B.Matkowsky,A.Bayliss,Coupled KS-CGL and coupled Burgers-CGL equations for flames governed by a sequential reaction,Physica D, (1999),253-298.

[2]F.A.Williams,F.Williams,Combustion Thoery,Benjamin Cunmmings:Menlo Park, 1985.

[3]J.Pelaez,A.Linan,Structure and stability of flames with two sequential reactions,SIAM J.Appl.Math.,45(1985),503-522.

[4]J.Pelaez,Stability of premixed flames with two thin reaction layers,SIAM J.Appl. Math.,47(1987),781-799.

[5]A.A.Nepomnyashchy,Order parameter equations for long wavelength instabilities,Physica D,86(1995),90-95.

[6]G.I.Sivashinsky,Nonlinear analysis of hydrodynamic instability in laminar flames I. Derivation of basic equations,Acta Astro.,4:11-12(1977),1177-1206.

[7]D.L.Li,B.L.Guo,X.H.Liu,Existence of global solution for complex Ginzburg Landau equation in three dimensions,Appl.Math.J.Chinese Univ.Ser.A,19:4(2004),409-416.

[8]D.L.Li,B.L.Guo,X.H.Liu,Regularity of the attractor for 3-D complex Ginzburg-Landau equation,Acta Math.Appl.Sin.,English Series,27:2(2011),289-302.

[9]J.M.Ghidaglia,B.Heron,Dimension of the attractor associated to the Ginzburg-Landau equation,Physica D:Nonlinear Phenomena,28:3(1987),282-304.

[10]B.L.Guo,The existence and nonexistence of a global smooth solution for the initial value problem of generalized Kuramoto-Sivashinsky type equations,J.Math.Res.Exposition,11:1(1991),57-70.

[11]B.L.Guo,The nonlinear Galerkin methods for the generalized Kuramoto-Sivashinsky type equations,Adv.Math.,22:2(1993),182-184.

[12]C.M.Postlethwaite,M.Silber,Spatial and temporal feedback control of traveling wave solutions of the two-dimensional complex Ginzburg-Landau equation,Physica D:Nonlinear Phenomena,236:1(2007),65-74.

[13]J.A.Sherratt,M.J.Smith,J.D.M.Rademacher,Patterns of sources and sinks in the complex Ginzburg-Landau equation with zero linear dispersion,SIAM J.Appl.Dyn. Syst.,9:3(2010),883-918.

[14]G.G.Doronin,N.A.Larkin,Kuramoto-Sivashinsky model for a dusty medium,Math. Meth.Appl.Sci.,26:3(2003),179-192.

[15]T.MacKenzie,A.J.Roberts,Accurately model the Kuramoto-Sivashinsky dynamics with holistic discretization,SIAM J.Appl.Dyn.Syst.,5:3(2006),365-402.

[16]A.A.Golovin,A.A.Nepomnyashchy,B.J.Matkowsky,Traveling and spiral waves for sequential flames with translation symmetry:Coupled CGL-Burgers equations,Physica D,160(2001),1-28.

[17]B.L Guo,X.L.Wu,Global Existence and Nonlinear Stability for the Coupled CGLBurgers Equations for Sequential flames inRN,arXiv:1310.4326[math.AP](2013).

[18]C.G.Guo,S.M.Mei,B.L.Guo,Global smooth solutions of the Gebeealized KSCGL equations for flames governed by a sequential reaction,Commun.Math.Sci., 12:8(2014),1457-1474.

[19]L.C.Evans,Partial Dif f erential Equations,American Mathematical Society,1988.

[20]A.Friedman,Partial Dif f erential Equations,Reinhart and Winston,1969.

[21]A.Pazy,Semigroups of Linear Operators and Applications to Partial Dif f erential E-quations,Berlin:Springer,1998.

(edited by Liangwei Huang)

∗Manuscript received

†Corresponding author.E-mail:gbl@iapcm.ac.cn