集合资料同化方法的理论框架及其在海洋资料同化的研究展望

沈浙奇,唐佑民,2 *,高艳秋

（1 .国家海洋局第二海洋研究所卫星海洋环境动力学国家重点实验室,浙江杭州310012；2 .北大不列颠哥伦比亚大学环境科学及工程系,加拿大乔治王子城V2 N 4Z9）



集合资料同化方法的理论框架及其在海洋资料同化的研究展望

沈浙奇1,唐佑民1,2 *,高艳秋1

（1 .国家海洋局第二海洋研究所卫星海洋环境动力学国家重点实验室,浙江杭州310012；2 .北大不列颠哥伦比亚大学环境科学及工程系,加拿大乔治王子城V2 N 4Z9）

摘要:在海洋动力系统的数值模拟中,海洋资料同化是一种能够有效融合多源海洋观测资料和数值模式的方法。它不仅可以显著地提高数值模拟的效果,构造海洋再分析资料场,还能有效减少海洋和气候预报时模式初始条件的不确定性。因此,海洋资料同化对于海洋研究和业务化应用具有非常重要的意义。资料同化方法的研究一直是大气、海洋科学的热门课题之一。其中,集合卡尔曼滤波器（En K E）是一种有效的资料同化方法,自提出以来经过了20多年的发展和改进,已经在海洋资料同化中得到了广泛的研究和应用。近年来,随着动力模式的不断发展和计算能力的提高,粒子滤波器由于不受模型线性和误差高斯分布假设的约束,也逐渐成为了当前资料同化方法研究的热点。本文分析和总结了目前关于集合卡尔曼滤波器和粒子滤波器的一些最新理论研究结果,在贝叶斯滤波理论的框架下讨论了这两类算法的关联和区别,以及各自在资料同化实践中的优势和不足。在此基础上,我们探讨了粒子滤波器应用于海洋模式资料同化的主要困难和目前可行的一些解决方法,展望了集合资料同化方法研究的新趋势,为集合资料同化方法的进一步发展和应用提供理论基础。

关键词:资料同化；集合卡尔曼滤波器；粒子滤波器；非高斯噪声；贝叶斯滤波

1 引言

资料同化（Data Assimilation,也称数据同化）是一种能够有机结合数值模式和观测这两种海洋学研究基本手段的方法。资料同化的核心思想是在动力学模式的运行过程中不断地融合新的观测信息,以达成改进模式初值、优化模式参数、改进模式分析和预报效果的目的。通过引入资料同化,不仅能够有效地提高海洋模拟效果,减少海洋和气候预报初始条件的不确定性,还能够为缺少海洋观测的深海和边缘海提供再分析资料［1—2］,为海洋观测计划和数值预报模式物理量及参数等提供设计依据。因此海洋资料同化在现代物理海洋学的研究中占据了非常重要的地位［3—4］。

目前,资料同化方法主要分为两类:变分方法（Variational method）和序贯方法（Sequential method）。变分方法包括三维变分（3 D-VA R）和四维变分（4 D-VA R）［5—6］,其主要特点是利用数值最优化算法求解目标函数的最小化问题。而以集合卡尔曼滤波器（EnkE）［7］为代表的序贯方法则是基于统计估计理论［8］的递归方法。所谓的序贯（一般也翻译为顺序）,指的是在每次有观测的时刻就利用显式的更新公式进行一次同化,然后再将所得的分析场作为下一次预报的初始场。这两类方法在大气、海洋等诸领域都已经取得了巨大的成功［9—11］。这里我们主要关注集合卡尔曼滤波器［7,12］,相比于变分方法,其优点在于无需发展四维变分同化算法要求的切线性和伴随模式,在同化时也考虑预报误差的动力演变,并且可以显式地提供集合预报的初始扰动,因此近年来随着计算条件的改善已得到了广泛的应用,也成为当前资料同化方法研究的热点［13—14］。

另一方面,粒子滤波器（Particle Eilter）也是一种集合资料同化方法,它在动力系统的状态估计中有着非常广泛的应用。相比于集合卡尔曼滤波器,粒子滤波器算法不受模型状态变量和误差高斯分布假设的约束,可以用于任意非线性非高斯的动力系统。它通过采样方法近似表示模式状态场的概率分布密度函数,能更好地同化非高斯信息。但是受限于滤波退化等问题,粒子滤波器一直没有在海洋资料同化领域得到较大关注。近年来,随着粒子滤波器被成功应用于一些高维动力系统的资料同化［15—16］,粒子滤波器开始成为当前资料同化算法研究的一个热门方向［17］。

本文在第二部分简要介绍了集合卡尔曼滤波器和粒子滤波器的研究背景。第三部分在贝叶斯滤波的统一框架下推导了集合卡尔曼滤波器和粒子滤波器的算法,并从理论和实践两方面指出了两者的优势和不足。第四部分主要介绍了粒子滤波器算法研究的最新进展和主要挑战,最后则是对集合资料同化方法的总结和展望。

2 集合卡尔曼滤波器和粒子滤波器的研究背景

集合卡尔曼滤波器是在卡尔曼滤波器的基础上发展起来的。对于线性的模式和高斯分布的噪声系统,经典的卡尔曼滤波器给出了精确的最优解［18］。而对于非线性的模式,最直接的处理方法是将卡尔曼滤波器应用于该模式的一阶线性化近似,得到相应的近似解,这种方法被称为扩展卡尔曼滤波器（E K E）。实际上,无论是经典的卡尔曼滤波器还是扩展卡尔曼滤波器,都需要在更新系统状态场的同时,计算和保存背景场的误差协方差矩阵,这在状态场空间维数非常巨大的海洋模式资料同化中是难以实现的。同时,扩展卡尔曼滤波器中的线性化过程会引起很大的截断误差,造成同化结果的偏差。这几点都极大地妨碍了扩展卡尔曼滤波器在实际海洋资料同化中的应用。

Evensen于1994年提出了集合卡尔曼滤波器［7］,通过采用蒙特卡洛的思想来避免模式线性化和直接计算预报误差协方差的困难。集合卡尔曼滤波器在算法上的最大突破是引入了集合的概念,即通过多次积分模式来得到预报集合,并使用预报集合的经验协方差来更新所有的集合成员,得到分析集合。经验协方差是一个统计上的概念,指的是根据有限的样本计算得到的协方差矩阵。当集合成员的数目趋于无穷的时候,可以证明预报集合的经验协方差趋向于预报误差协方差的真值。一方面,集合卡尔曼滤波器通过积分完整的非线性模式来进行预报,避免了截断误差的产生；另一方面,集合卡尔曼滤波器使用实时计算的经验协方差矩阵来代替卡尔曼滤波器公式中出现的预报误差协方差矩阵,避免了协方差矩阵的储存和更新,以及伴随而来的巨大运算量。由于集合卡尔曼滤波器的提出,卡尔曼滤波器的思想得以应用于大型海洋模式的资料同化。在此之后,基于相同的集合化思想,一系列集合卡尔曼滤波器的衍生算法也相继被提出,如集合转移卡尔曼滤波器（E T K E）［19］,集合调整卡尔曼滤波器（E A K E）［20］,集合平方根滤波器（En-SRE）［21］等。这些方法虽然基于不同的角度来推导状态场和误差协方差矩阵的更新公式,但归根结底还是都使用了经典卡尔曼滤波器。

在此基础上,一些新的方法和技巧也陆续被引入来改善集合卡尔曼滤波器及其衍生方法在实际同化中的表现。比如,协方差松弛（covariance inflation,也被称为协方差膨胀）技术被引入来改变集合的离散度,从而解决因集合成员数目较少或者模式误差的影响而产生的协方差矩阵低估问题［22］。协方差的松弛系数最初使用的是根据经验给定的固定参数。但在近几年,一系列选择自适应松弛系数的方法也得到了很大的发展［23—24］。在集合卡尔曼滤波器的同化实践中,模式的初值、大气外强迫、模式开边界和河流输入等因素的扰动会在很大程度上影响集合的离散程度,一些研究也表明使用这些扰动构成预报集合能大大改善集合卡尔曼滤波器的同化效果［25］。

集合卡尔曼滤波器及其衍生方法能成功应用于大型海洋模式,另一个很主要的原因是局地化策略［26］的应用。一般来说,对于空间上不稳定的动力系统,分析格式并不能修正距观测距离较远的格点处的误差,相反,由于分析空间范围过大,反而会在距离较大的格点之间产生虚假的相关性。局地化策略相当于在观测周围区域内的一个低维子空间内进行分析,使得观测不再影响给定距离之外的格点。通过引入局地化,除了能够避免上述的虚假相关性以外,还能大大减少预报误差协方差矩阵的非零元素数目,降低分析的运算量。所以,局地化方案的选取和局地化参数的设置对于集合卡尔曼滤波器的同化效果具有很大的影响,其理论研究在同化领域仍然是热门方向［27—28］。

集合卡尔曼滤波器目前在国际上得到了广泛的研究和应用。加拿大气象中心于2005年最先在其全球集合预报系统中采用了业务化的集合卡尔曼滤波器来提供预报的初始条件［29］。W W RP/T H O RPE X国际计划于2008年在阿根廷的布宜诺斯艾利斯开展了“比较集合卡尔曼滤波器和四维变分”的专题研讨。该研讨会通过将集合卡尔曼滤波器与当前主流业务化预报系统中采用的四维变分方法进行比较,进一步地阐明了集合卡尔曼滤波器方法的业务化前景［30］。另外,挪威2010年基于H Y C O M海洋模式,利用En-K E方法建立了北大西洋海洋预报系统［31］。美国N O A A/G ED L基于M O M 4模式,利用En K E方法建立了全球气候分析与预报系统［32］。

虽然集合卡尔曼滤波器及其衍生算法都得到了广泛的关注和认可,但是有必要指出卡尔曼滤波公式本身采用的一些假定实际上限制了上述方法的同化效果。如前述,只有在保证数值模式为线性模式,并且预报误差和观测误差都是高斯分布的前提下,卡尔曼滤波器才提供最优的解。卡尔曼滤波器的公式本身只包含状态场的平均值和协方差信息,它实际上默认了公式中涉及到的所有误差（预报误差和观测误差）都是呈高斯分布的。而一个简单的事实是,模式的非线性会不可避免地将误差的分布变成非高斯分布［33］。对集合卡尔曼滤波器的渐近分析也表明,即使同化系统中的预报初值误差和观测误差都是高斯分布的,分析集合的经验分布也会趋向于一个错误的极限——即与一般的贝叶斯滤波器的极限不同（贝叶斯滤波理论将在第三部分展开讨论）。换句话说,即使我们的计算资源无限,集合卡尔曼滤波器也无法保证获得最可靠的分析。在此背景下,集合卡尔曼滤波器以外的非线性集合同化方法在近些年得到了迅速发展［33—34］,其中一类典型的方法就是粒子滤波器。

相比于集合卡尔曼滤波器,粒子滤波器不受模型状态变量和误差高斯分布假设的约束,可以用于任意非线性非高斯的动力系统。因此粒子滤波器从21世纪初开始就被广泛应用于地球系统数据同化［35—36］,并成为了一个热门的研究方向。实际上,粒子滤波器并不是一种很新的概念。早在20世纪50 - 60年代, Ham mersley等就提出了一种称为序贯重要性采样的蒙特卡洛方法［37］,它的基本原理是通过离散的随机样本逼近状态场的概率分布密度函数。但是,由于计算复杂性和样本退化的问题,该方法在相当长的一段时间内没有取得多大的进展。直到1993年Gordon等提出了重取样的概念［38］,在一定程度上克服了算法的退化问题,才出现了第一个真正可行的序贯蒙特卡洛方法。该方法称为自助式粒子滤波器,被公认为是现代粒子滤波器的基石［39］。所谓的粒子实际上就是用来近似表示概率分布密度函数的样本,这和集合卡尔曼滤波器中的集合成员是相对应的概念。粒子滤波器利用观测来更新粒子的权重,并通过加权来逼近后验概率分布密度。最初的序贯重要性采样使用转移概率密度函数作为重要性采样函数,在每一次观测更新的时刻利用递推关系来改变各个粒子的权重,但不改变粒子本身的数值。随着迭代次数的增加,几乎肯定会出现粒子退化的问题。粒子退化指的是这样一种情况:随着同化的进行,少数粒子逐渐占据了几乎所有的权重,而大部分粒子的权重则基本可以忽略不计。如果出现了粒子退化,大量的计算成本会被用于更新对概率分布密度函数的贡献几乎为零的粒子,造成无法承受的运算负担。而过低的有效样本率也会导致后验估计的精度完全不可靠,无法改善预报的效果。自助式粒子滤波器实际上就是在序贯重要性采样的基础上加入了重取样过程,因此也被称为重取样粒子滤波器（SIR-PE）。重取样的基本思想是根据后验分布中的各粒子权重重新分配粒子集,将权重较大的粒子复制多份,同时消除权重很小的粒子。在这个过程中粒子的总数保持不变,最后得到的是等权重的粒子集。重取样的依据是粒子的权重,具体的实施方法有很多种,包括多项式重取样、残差重取样、系统重取样等［40］。总之,通过重取样,可以消除权重较小的粒子,避免退化的发生。但是这样的处理也会导致重取样后的粒子几乎都是少数几个粒子的后代,粒子的多样性明显减弱,不能充分表征后验概率密度函数,该现象称为粒子贫化问题。为解决贫化问题,Kotecha和Djuric提出了高斯粒子滤波器（Gaussian particle filter）及高斯和粒子滤波器（Gaussian su m particle filter）［41—42］,Xiong等提出了后验高斯重取样的粒子滤波器［43］,Nakano等提出了融合粒子滤波器［44］,这些方法对于抑制贫化都起到了一定的效果。

对于维数较小的模式和同化系统,重取样过程能够解决粒子的权重退化问题。但对于海洋模式资料同化中涉及的高维模式,结果并没有那么乐观。Snyder等系统地研究了粒子滤波中的退化问题,并且指出:为了防止粒子的权重发生退化,粒子的数目必须随着状态空间的维数而指数增长,即使是引入了重取样过程,也无法从根本上解决粒子数目需要随系统维数增长的难题［45］。对于海洋模式资料同化中的高维模式来说,这样的计算量显然是难以接受的。简而言之,“维数灾难”（curse of dimensionality）［46］问题是粒子滤波器应用于实际大气海洋研究中的高维模式的最大障碍。Van Leeuwen详细总结了高维模式系统资料同化中的粒子滤波算法,在重申了维数困难的前提下,也列出了几种已知可行的粒子滤波器,如引导粒子滤波器、边际粒子滤波器、辅助粒子滤波器等［36］。大体上来看,目前主要的努力方向仍然在序贯重要性取样和重取样的结合方法上面。

最初提出的序贯重要性取样使用转移密度函数作为重要性取样函数（也叫做建议分布密度）,也就是说直接利用前一步的粒子进行预报,将预报的结果不加处理地作为新的粒子。这种情况下,算法本身不改变粒子的数值,而只是利用粒子与观测的相近程度更新权重。当状态场空间的维数很大时,很容易由于粒子与观测的差别太大而无法获取有意义的权重,这就是退化现象。相对地,如果使用一个依赖于观测值的建议分布来产生新的粒子,就可以人为地使粒子更接近观测值,避免计算得到的权重过小,在一定程度上也能够降低退化发生的几率。基于此前提可以得到最优建议分布。需要注意的是,这里的“最优”并不是指同化的效果最优,而是指根据这种建议分布下产生的粒子计算出来的权重的方差最小,能最大限度地避免退化的发生［47］。在绝大多数情况下,这种最优建议分布无法解析求得,目前热门的方法都是在试图去近似表示这个最优建议分布。这些方法在第四部分具体阐述。

3 贝叶斯理论框架下的集合卡尔曼滤波和粒子滤波

资料同化在数学上是动力学系统的状态估计问题,由状态空间方法描述。状态空间模型分为状态预报模型和观测模型两部分,二者在资料同化系统中又分别被称为模式算子和观测算子。模式算子对应着数值模式,在不同的动力学系统中可以分别是大气模式、海洋模式、陆面过程模式或水文模式等。模式算子描述的是状态变量场随时间的演变,一般情况下可以将它理解成为一个“黑匣子”,利用给定的初值和外强迫场得到具有一定准确性的预报场。观测算子则描述了状态场和观测资料的对应关系:对于直接观测来说,一般需要使用空间插值的方法将模式的网格点投影到观测点；而对于遥感等非直接观测来说,也可能需要使用非线性的观测模型来将状态变量和观测变量相关联,比如遥感辐射传输模型。状态空间模型可以用以下公式描述:

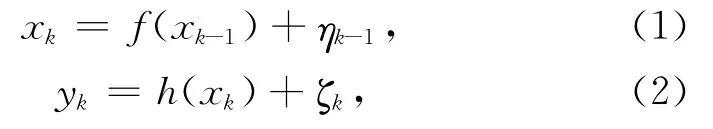
式中,xk代表离散时间tk上的状态变量场,yk代表相同时刻的对该状态场的观测。η和ζ分别代表了随机的模式误差和观测误差,二者的概率分布密度函数可以是任意形式的（但在很多情况下两者都被假设为高斯分布）,并且假设两者互不相关。

贝叶斯理论是集合滤波资料同化方法的理论基础。基于贝叶斯理论的贝叶斯滤波器从原理、方法和符号系统上为序贯资料同化方法提供了一个统一的框架［48—49］。贝叶斯滤波器以概率分布密度函数为对象,其目标是:在初始状态场的概率分布密度函数p（x0）为已知的前提下,利用模式算子式（1）和观测算子式（2）递归地更新状态场的后验概率分布密度函数p（xk|y1:k）,其中y1:k代表从时刻t1到tk的所有观测,xk| y1:k意味着利用所有这些观测信息对xk作出的估计。贝叶斯滤波器的基本前提有两个:第一,模式状态服从一阶M arkov过程p（xk| x0:k- 1）= p（xk| xk- 1）,也就是说每一步预报的结果只依赖于预报初值,与历史状态场不相关；第二,观测值与模式当前状态场相互独立。

递归贝叶斯滤波器的每个滤波循环分为两步——预报和更新。其中的预报过程利用前一时刻状态场的后验概率分布密度函数p（xk- 1|y1:k- 1）得到当前时刻的先验概率分布密度函数p（xk| y1:k- 1）。假设p（xk- 1| y1:k- 1）已知,根据M arkov过程转移密度的Chap man-Kolmogorov方程,下一时刻状态场的先验概率分布密度为［50］:

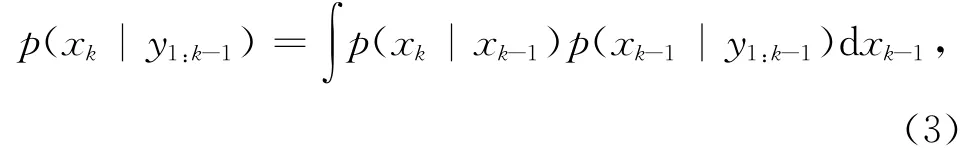
式中,p（xk| xk- 1）称为转移概率密度函数,等价于模式误差的概率表达。当模式误差取成式（1）中的加法噪声形式时,可以简单地认为:

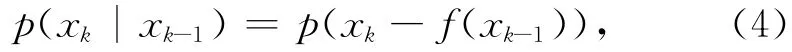
这也是η的概率分布密度函数。先验概率分布密度函数刻画了我们仅根据模式而不利用观测信息得到的知识,其分布密度函数仅与模式初值和模式误差的分布相关。而更新过程（在同化术语中一般称为分析）通过整合观测信息来更新状态场,得到后验概率分布密度。根据贝叶斯定理,系统状态的后验概率分布密度函数为:

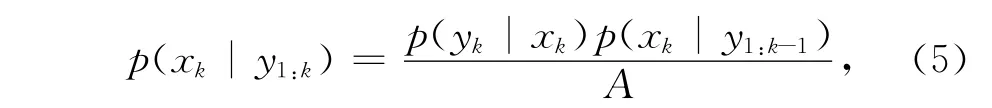
公式（3）和（5）完整地表达了序贯资料同化方法的贝叶斯递归滤波形式:即模式系统的动态演进和观测信息的不断融合,在考虑模型和观测误差的基础上,不断地更新对系统状态的估计。贝叶斯滤波从原理上为各种资料同化方法勾勒了一个统一的框架,集合卡尔曼滤波器和粒子滤波器的具体算法都可以在此基础上得到。

3.1 集合卡尔曼滤波器

如果假设式（5）中先验概率分布密度函数、似然函数和后验概率分布密度函数为协方差矩阵分别为Pf、R和Pa的多维正态分布,展开式（5）并对公式两边取对数,再使得Pa最大化,可以得到如下的目标函数

这与从线性无偏估计得到的三维变分的目标函数相同［5］。为了方便表示,式（7）中使用xfk代替先验的状态场xk| y1:k- 1。由式（7）很容易推导出经典卡尔曼滤波器的分析公式:

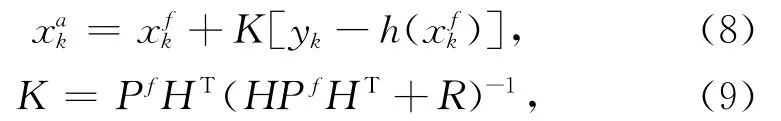
式中,H为h的线性化算子（公式（7）～（9）的具体推导见附录1）。

集合卡尔曼滤波器中采用了集合的概念,预报集合中的每一个成员实际上是通过对不同的初值进行积分得到的。使用预报场的集合成员可以计算其经验协方差矩阵,即

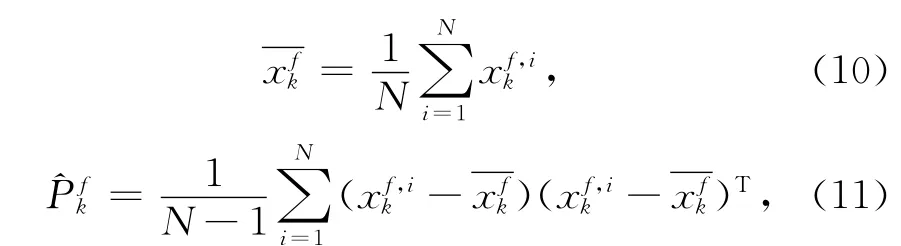
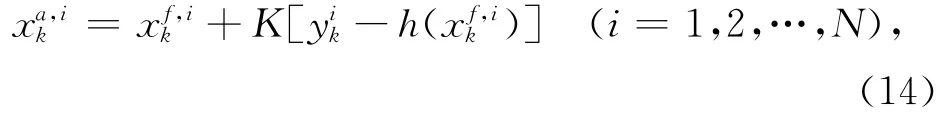
3.2 粒子滤波器

与集合卡尔曼滤波器中采用的高斯分布假设不同,粒子滤波器使用一系列粒子的加权和来表示各阶段的概率分布,并且直接使用贝叶斯滤波式（3）和（5）来进行预报和分析。假设前一时刻的后验概率分布密度函数可以表示为如下形式:

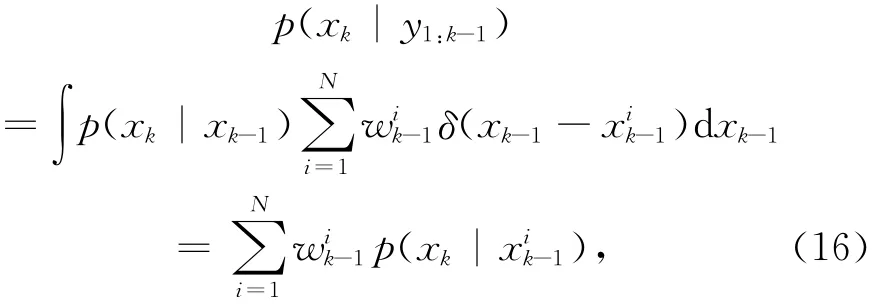
这是一个以xk为变量的连续概率分布密度函数,由,i = 1,2,…,N｝这一组基构成。接下来使用式（5）进行分析,把式（16）代入,就可以得到后验概率分布密度函数如下:

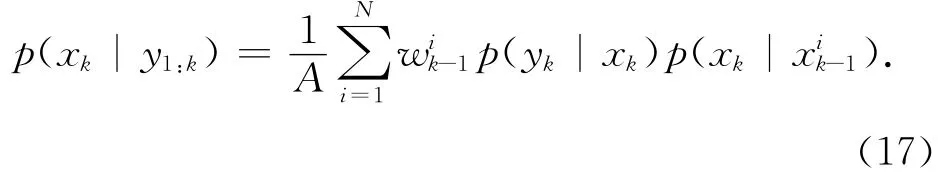
这依然只是一个连续的分布密度函数,我们需要对其取样来得到与式（15）对应的δ函数的有限组合形式。理论上,我们需要根据一个建议分布q（xk）来取样得到新的粒子,也就是说令-）,那么式（17）可以改写为:

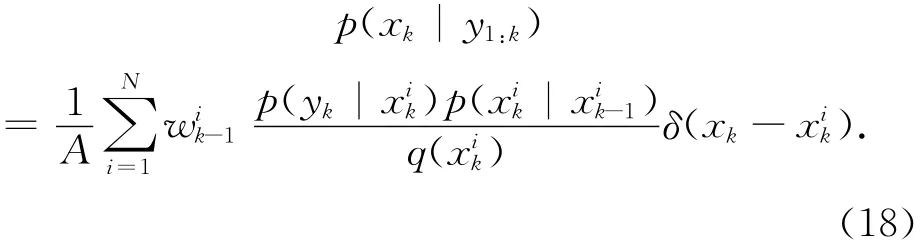
假定每一个贝叶斯滤波循环中的权重之和都为1,那么因子A可以看作是一个归一化因子。因此,权重的递归关系可以表示为:该式中的正比符号意味着需要一个归一化过程使得等式的两边相等。

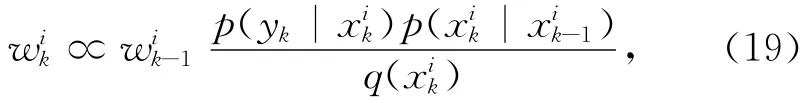
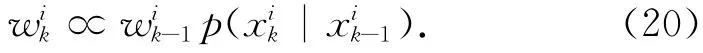
也就是说,仅使用似然函数的值就能够更新每个粒子的权重。

基础的粒子滤波器算法不需要使用类似集合卡尔曼滤波器中的预报场（xf）和分析场（xa）这两套不同的符号来区别分析前后的粒子。这是因为先验的粒子（xk| y1:k- 1）和后验的粒子（xk| y1:k）在数值上并没有发生变化,变化的仅仅是两者的权重。这一点也是退化问题发生的根源。为了处理退化问题, Gordon等［38］引入了重取样过程,将其应用于式（20）对应的权重更新之后的加权集合。借用Van Leeuwen［36］综述论文中的示意图（图1）,可以很清楚地看出重取样过程的实质就是根据权重的大小重新分配样本。图中黑点的大小代表了粒子的权重, 图1a由于没有采用重取样过程,很快就会发生所有权重集中在同一个粒子上的退化现象；而图1b在求得权重之后,将权重较大的粒子复制多份,同时消除权重较小的粒子,使用这样的粒子集进行预报和更新就不容易产生退化。重取样算法有很多种,但其基本原则大致相同［40］,加入重取样的基本粒子滤波器也常常被叫做重取样粒子滤波器。

3.3 集合卡尔曼滤波器和粒子滤波器的关联和比较

如前面所述,贝叶斯滤波理论提供了一个统一的框架,各种资料同化方法都可以由此推出。粒子滤波器通过蒙特卡洛的思想直接应用贝叶斯滤波理论,当粒子数目趋向于无穷的时候,它可以收敛到贝叶斯滤波器的结果［54］。而集合卡尔曼滤波器则不同,它采用了高斯近似来逼近贝叶斯滤波器的结果。也就是说,集合卡尔曼滤波器衍生的方法预先假定了贝叶斯式（3）和（5）中涉及到的所有概率分布密度都是高斯分布的。理论研究证明:在一个分析循环中,只要模式是非线性的,即使初始场、模式噪声和观测噪声都服从高斯分布,当集合尺寸N趋于无穷时,预报集合和分析集合的分布密度函数也都会趋向于错误的极限［55］。也就是说两个集合的极限分布会不同于贝叶斯预报场式（3）和贝叶斯分析场式（5）的分布。关于这一点有非常严密的数学证明,但是最直观的解释还是因为模式的非线性会不可避免地带来分布的非高斯性。所以高斯分布的初始集合加上高斯噪声会产生非高斯的预报集合,然后使用预报集合的高斯近似进行分析,也会导致后验分布的偏差。该理论指出的是集合卡尔曼滤波器类的方法在同化效果上的极限,即在集合成员数目足够多时,集合卡尔曼滤波器的同化效果会逐渐趋于一个不正确的稳定结果。

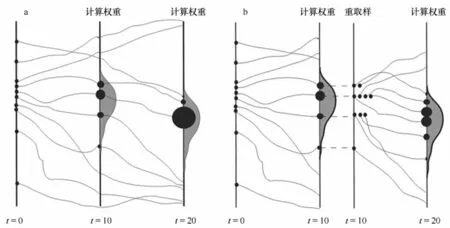
图1 粒子滤波器中的粒子退化与重取样示意图［36］Eig .1 The schematic diagram for filter degeneracy and resampling in SIR-PE［36］黑点代表粒子,点的大小代表权重大小Black dot represents the particle,the size of dot represents the weight value

目前在集合资料同化方法的研究中,集合卡尔曼滤波器相较于粒子滤波器得到了更多的关注和应用,其最主要的原因是由于集合卡尔曼滤波器及一系列的衍生方法所需要的计算成本较小。这里的计算成本主要体现在集合成员数量上。以前面介绍的集合卡尔曼滤波器和重取样粒子滤波器为例,一般来说,即使对于状态空间场维数巨大的数值模式,集合卡尔曼滤波器使用10～100个左右的集合成员就能保证较好的同化效果［56］。而相比较而言,重取样粒子滤波器需要非常大的集合来防止发生退化。更糟的是,在重取样粒子滤波器中这个数目还会随着问题的维数而增长。Bocquet等［33］和Nakano等［44］使用了洛伦茨63（L63）模式［57］和洛伦茨96（L96）模式［58］对这两种方法进行了一系列的比较。结果表明,对于只有3维的L63模式,重取样粒子滤波器需要200个左右的集合成员来使得同化结果的均方根误差（R M SE）明显小于集合卡尔曼滤波器；而对于10维和40维的L96模式,则分别需要10 000和30 000以上的集合成员数才能确保重取样粒子滤波器的优势。

两者比较的结论:集合卡尔曼滤波器非常适用于状态空间维数巨大的动力系统,即使集合成员的数目比较小,该方法也能够给出后验分布的前两阶统计矩（均值和协方差）的合理估计。再加上集合卡尔曼滤波器可以采纳局地化方案以抑制长距离的虚假相关,进一步地避免了发生类似粒子滤波器中的退化。与之相比,重取样粒子滤波器更适合于维数较小的强非线性系统,它能够突破高斯假设的限制,达到更好的同化效果。一旦系统的维数增加,“维数灾难”问题将直接导致重取样粒子滤波器的计算成本无法负担。因此尽管有不少文章对重取样粒子滤波器与集合卡尔曼滤波器进行比较,但是在实际高维海洋模式的资料同化中,重取样粒子滤波器是无法使用的［45］。如何在高维的模式系统中使用粒子滤波器仍然是一个极具挑战性的问题,是当前集合资料同化方法研究的热门方向［29,31］。目前的研究表明,在粒子滤波器算法中采用观测依赖的建议分布,能够极大地降低权重退化的几率,降低运算成本,这也是当前粒子滤波器研究的热门方向。

4 粒子滤波器算法的新进展和研究重点

由3.2可知,所有的粒子滤波器都基于使用Dirac-Delta函数的加权和形式来表示完整的概率分布密度函数,但是权重的更新公式根据不同的算法又各有不同。这是因为更新公式（18）中涉及的建议分布密度函数q（xk）可以选择不同的形式。为理解建议分布这个概念,假设两个概率分布密度函数分别记为p（x）和q（x）,根据q（x）随机取样得到的样本集合｛xi,i = 1,…,N｝显然逼近于q（x）的分布。进一步地,假如定义权重为wi= p（xi）/q（xi）,那么这些加权样本｛xi,wi｝就会逼近于p（x）的分布。这两个分布密度函数p（x）和q（x）在统计上分别被称为目标分布和建议分布。

重取样粒子滤波器以转移概率密度函数p（xk| xk- 1）为建议分布,推出形式上比较简单的递推公式（19）。考虑到转移密度函数等价于模式噪声的概率表达,可以看到重取样粒子滤波器实际上不对预报粒子进行任何的处理,而是直接使用以上一步的分析粒子为初值得到的预报粒子集合去进行分析。当状态场的空间维数很大时,因为所有粒子的权重都太小而较容易产生退化。最近的研究结果都指出,使用依赖于观测的建议分布q（xk,yk）可以在进行分析之前对预报粒子进行一定的处理,使其更接近观测资料,减少权重退化的几率。这一类的研究是当前粒子滤波器方法的研究热点。

最理想的情况是令q（xk,yk）= p（xk| xk- 1,yk）,这个分布在相关文献中被称为最优建议分布,它可以使得tk时间新产生的粒子集合｛xik｝对应各权重｛wi｝的方差最小。由贝叶斯定理可得到:

将式（22）带入式（18）就得到:

对比式（19）可以看出,由式（21）更新的wi与从建议分布中随机选取的样本xik并不相关,因此不会增加权重集合的方差。在实际同化中,考虑到对观测的依赖性,这个最优建议分布的表达式很难通过计算得到。因此,目前大量工作的重点都在于逼近最优分布或者在特定的情况下将其简化。

M orzfeld等［59］利用一种依赖于有效平均值的方法求解得到了p（xk| xk- 1,yk）的解析表达式。该表达式适用于模式和观测算子都含有加法高斯噪声,且观测算子为线性函数（记为H）的简单情况。Snyder给出了具体的解析式［47］如下:假设同化系统为

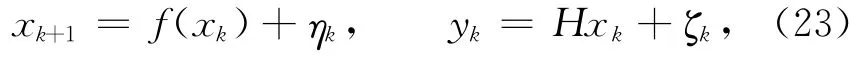
式中,ηk～N（0,Q）,ζk～N（0,R）。这里的～p（x）代表样本是依据概率分布密度函数p（x）随机取样得到的,N（0,Q）代表均值为0,协方差为Q的（多元）高斯分布。根据Doucet等［60］的理论,由于模式噪声η服从高斯分布可得xk| xk- 1～N（f（xk- 1）, Q）,利用标准的卡尔曼滤波器公式,可得xk| xk- 1,yk～N（,P）,其中

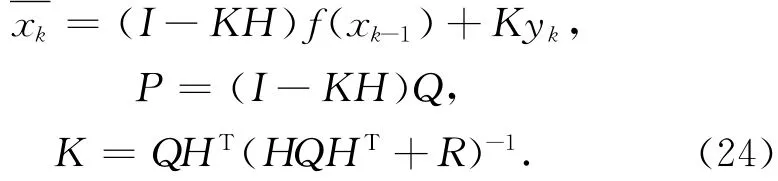
也就是说,最优建议分布p（xk| xk- 1,yk）可以写成高斯分布N（,P）的形式。而相应的权重更新公式（21）也可以利用以下关系得到:

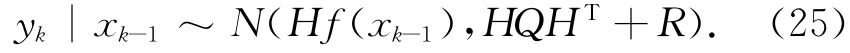
上面提到的是比较理想的情况,在实践中鉴于计算量的考虑,一般使用集合成员来近似表示这些高斯分布。Papadakis等［61］通过比较总结了集合卡尔曼滤波器和重取样粒子滤波器两种方法的特点,并在此基础上提出了加权集合卡尔曼滤波器（weighted ensemble Kalman filter）以结合两者优势。虽然该方法的名字中含有“卡尔曼滤波器”,但它实际上是一种粒子滤波器。其基本原理相当于使用集合卡尔曼滤波器的后验概率分布（由前面的论述很容易知道它服从高斯分布）作为最优建议分布的一个近似,在此基础上求得权重并用重取样方法更新集合（加权集合卡尔曼滤波器的具体算法参考附录2）。可以看出,加权集合卡尔曼滤波器在算法的实行上非常简便,可以看作是依次执行集合卡尔曼滤波器和重取样粒子滤波器,只是在权重的更新公式上进行了一定的修改。这也是这种粒子滤波器会被叫做“加权集合卡尔曼滤波器”的主要原因。加权集合卡尔曼滤波器自提出以来得到了很多的关注和应用,具有进一步研究和应用的价值［62—63］。

同样地,为了结合集合卡尔曼滤波器和重取样粒子滤波器这两类方法的特点,Erei和Kunsch提出了集合卡尔曼粒子滤波器（ensemble Kalman particle filter）［64］。与加权集合卡尔曼滤波器的思想（使用集合卡尔曼滤波器的分析作为建议分布）不同,集合卡尔曼粒子滤波器通过使用一个可调制的参数控制集合卡尔曼滤波器和重取样粒子滤波器两阶段的比重,构建了一个混合高斯模型（Gaussian Mixture M odel）,以达成可计算性和同化非高斯信息能力的平衡。我们最新的工作进一步发展了这种方法,使之能够适用于非线性的观测算子［65］。数值实验表明,集合卡尔曼粒子滤波器能非常有效地改善集合卡尔曼滤波器在强非线性模式系统中的同化效果。但是因为自适应算法调制参数的计算量比较大,我们还需要一些更深入的研究才能将其应用到较高维的系统。

除了上述的方法以外,其他一些最新的粒子滤波器也大多集中于使用这种依赖于观测的建议分布。例如,Van Leeuwen［66］通过充分改进建议分布提出了一种完全非线性的粒子滤波器,他们称之为等权重粒子滤波器（Equivalent W eights Particle Eilter）。等权重粒子滤波器的基本思想是在模式运行中对每一个粒子求解一个目标为“使得各粒子的权重大致相等”的最优化问题,从而避免退化的发生。这种方法也受到了大量的关注［67 - 68］。此外,Chorin等提出的隐式粒子滤波器（Implicit Particle Eilter）［59,69］,Luo等提出的带残量拖曳的粒子滤波器（Particle Eilter with Residual Nudging）［70］,这些方法也在一定程度上促进了粒子滤波器的发展。

5 总结和展望

随着各种观测数据的迅猛增多,以及大气海洋数值模式的不断发展,如何充分利用各种观测数据以满足数值模式和预报的需要是一个非常重要的课题。作为连接观测和模式的桥梁,资料同化技术日益受到关注,并得到深入的研究与广泛的应用。

本文着重探讨了集合资料同化方法的一些研究背景和发展现状,主要包括两大类的方法:集合卡尔曼滤波器和粒子滤波器。集合卡尔曼滤波器是为数不多的由海洋学者率先提出的资料同化方法［7,12］,在海洋资料同化之中已经有了非常广泛的应用,其同化效果也得到了普遍认可。与另一种在业务化中普遍使用的变分方法相比,集合卡尔曼滤波器的主要优势如下:（1）使用流依赖的背景场协方差矩阵；（2）无需使用切线性模式和伴随模式；（3）容易并行化使用。国内外已经有了非常多的关于集合卡尔曼滤波器方法本身的研究,探讨了初始集合如何产生、如何使用协方差松弛技术、如何进行局地化以及如何进行参数估计等方面问题。在应用方面,集合卡尔曼滤波器也被广泛用于诸如太平洋海洋高度计资料同化［71］、E NSO的预报［72］和印度洋海面高度异常的短期预报［73］等方面。预计在不久的将来,还会在参数估计以及耦合模式的资料同化方面得到更多的应用。然而,集合卡尔曼滤波器也有一些不足:比如需要一定的集合样本数目来避免背景场协方差的低估；积分模式的计算成本较高等。从原理上看,还可以知道集合卡尔曼滤波器及其衍生的方法都隐含了高斯分布假设——即假定预报误差、模式误差和观测误差都服从高斯分布。在该假设下,更新公式只使用前两阶的统计矩（均值和协方差）来刻画集合的概率分布密度函数。当实际预报集合不服从高斯分布时,同化效果会有一定的限制。

作为另一类的集合资料同化方法,粒子滤波器被更多地用于机械、计算机和信号处理等工程领域,只是在近几年才逐渐被认识到可用于地球系统的资料同化［16］,并逐渐成为了研究的热门方向之一。从理论上看,包括集合卡尔曼滤波器和粒子滤波器在内的序贯同化方法都可以从贝叶斯滤波的框架推导得到。相应于集合卡尔曼滤波器的高斯分布假设,粒子滤波器对于预报集合的分布不作任何的先验假定,而是采用大量的样本去估计完整的概率分布密度函数。在贝叶斯框架内,我们非常容易理解这两类方法的强项和缺陷:集合卡尔曼滤波器的分析场分布随着N的增大能够很快收敛,但是无法收敛到由贝叶斯滤波器给出的真实的极限；粒子滤波器能够收敛到真实的极限,但是需要的集合成员数量N过于巨大,难以在实际同化中实现。一些简单模式中的比较［33］也揭示了这一点。

如何在高维的模式系统中使用粒子滤波器一直是一个挑战性的问题,还没有得到彻底的解决,也是当前研究的一个热门方向。理论已经证明了基本的重取样粒子滤波器无力解决高维系统中的滤波退化问题（“维数灾难”）,需要更多的努力来避免粒子的效率过低。通过对一系列最新研究的总结,本文指出解决粒子滤波器计算量大的一个主要手段是使用依赖于观测的建议分布。理论上的最优建议分布难以在实际同化中计算得到,所以大部分当前可行的粒子滤波器都采用它的近似来作为产生新样本的建议分布。在当前比较受关注的新兴粒子滤波器中,本文选择加权集合卡尔曼滤波器做了较详细的介绍。这不仅仅是因为加权集合卡尔曼滤波器的算法表述比较简明,更重要的是,它在集合卡尔曼滤波器和粒子滤波器之间构筑了一个桥梁,非常好地展现了两者的区别和关联。此外,本文也提到了一些当前热门的粒子滤波器。

总的来说,集合资料同化方法目前正处于快速发展中。随着当前数值模式复杂性的不断提高,计算能力的不断增长,集合卡尔曼滤波器和粒子滤波器的重要性正在逐渐凸显。当然,两类资料同化方法的研究中都还有非常多急需解决的难题,本文通过对一些理论工作的整理和总结,旨在为将来集合资料同化方法的发展提供一些理论基础。

参考文献:

［1］ Yan C,Zhu J,Xie J . An ocean reanalysis system for thejoining area of Asia and Indian-Pacific ocean［J］. Atmospheric and Oceanic Science Letters, 2010,3（2）:81 - 86 .

［2］ Han G,Li W ,Zhang X,et al. A regional ocean reanalysis system for coastal waters of China and adjacent seas［J］. Advances in Atmospheric Sciences,2011,28（3）:682 - 690 .

［3］ 马建文,秦思娴.数据同化算法研究现状综述［J］.地球科学进展,2012,27（7）:747 - 757 . M a Jianwen,Qin Sixian . Recent advances and development of data assimilation algorith ms［J］. Advancesin Earth Science,2012,27（7）:747 - 757 .

［4］ 李宏,许建平.资料同化技术的发展及其在海洋科学中的应用［J］.海洋通报,2011,30（4）:463 - 472 . Li H ong,Xu Jianpin . Development of data assimilation and its application in ocean science［J］. M arine Science Bulletin,2011,30（4）:463 - 472 .

［5］ Courtier P,Andersson E,Heckley W ,et al. The EC M W E implementation of three-dimensional variational assimilation（3 D-Var）.I:Eormulation ［J］. Quarterly Journal of the Royal M eteorological Society,1998,124（550）:1783 - 1807 .

［6］ Le Dimet E X,Talagrand O . Variational algorith ms for analysis and assimilation of meteorological observations:theoretical aspects［J］. Tellus A, 1986,38（2）:97 - 110 .

［7］ Evensen G .Sequential data assimilation with a nonlinear quasi-geostrophic model using M onte Carlo methods to forecast error statistics［J］.Journal of Geophysical Research:Oceans（1978 - 2012）,1994,99（C5）:10143 - 10162 .

［8］ Gelb A . Applied optimal estimation［M］. Boston:The MIT Press,1974 .

［9］ Evensen G . The ensemble Kalman filter:Theoreticalformulation and practicalimplementation［J］. Ocean Dynamics,2003,53（4）:343 - 367 .

［10］ Kalnay E . Atmospheric modeling,data assimilation,and predictability［M］. Cambridge:Cambridge U niversity Press,2003 .

［11］ Park S K,Xu L . Data Assimilation for Atmospheric,Oceanic and H ydrologic Applications（Vol.Ⅱ）［M］. Berlin:Springer Science & Business M edia,2013 .

［12］ Burgers G,Van Leeuwen P J,Evensen G . Analysis scheme in the ensemble Kalman filter［J］. M onthly W eather Review,1998,126（6）:1719 -1724 .

［13］ 刘成思,薛纪善.关于集合Kalman滤波的理论和方法的发展［J］.热带气象学报,2005,21（6）:628 - 633 . Liu Chengsi,Xue Jishan . The ensemble Kalman filter theory and method development［J］.Journal of Tropical M eteorology,2005,21（6）:628 -633 .

［14］ Gillijns S,M endoza O B,Chandrasekar J,et al. W hatis the ensemble Kalman filter and how well doesit work？［C］//Proceedings of the A merican Control Conference,2006 . Minneapolis,Minnesota,U SA,2006.

［15］ Bengtsson T,Snyder C,Nychka D . Toward a nonlinear ensemble filter for high-dimensional systems［J］.Journal of Geophysical Research,2003, 108（D24）:8775 .

［16］ M oradkhani H,Hsu K L,Gupta H,et al. U ncertainty assessment of hydrologic modelstates and parameters:Sequential data assimilation using the particle filter［J］. W ater Resources Research,2005,41（5）:W 05012 .

［17］ 毕海芸,马建文.粒子滤波算法在数据同化中的应用研究进展［J］.遥感技术与应用,2014,29（5）:701 - 710 . Bi Haiyun,M a Jianwen . Advancesin the study of partcilefilterin data assimilation［J］. Remote Sensing Technology and Application,2014,29（5）: 701 - 710 .

［18］ Kalman R E . A new approach to linear filtering and prediction problems［J］.Journal of basic Engineering,1960,82（1）:35 - 45 .

［19］ Bishop C H,Etherton B J,M aju mdar S J . Adaptive sampling with the ensemble transform Kalman filter .PartⅠ:Theoretical aspects［J］. M onthly W eather Review,2001,129（3）:420 - 436 .

［20］ Anderson J L . An ensemble adjustment Kalman filter for data assimilation［J］. M onthly W eather Review,2001,129（12）:2884 - 2903 .

［21］ Tippett M K,Anderson J L,Bishop C H,et al. Ensemble square root filters［J］. M onthly W eather Review,2003,131（7）:1485 - 1490 .

［22］ Li H,Kalnay E,Miyoshi T .Simultaneous estimation of covarianceinflation and observation errors within an ensemble Kalman filter［J］. Quarterly Journal of the Royal M eteorological Society,2009,135（639）:523 - 533 .

［23］ Miyoshi T . The Gaussian approach to adaptive covariance inflation and its implementation with the local ensemble transform Kalman filter［J］. M onthly W eather Review,2011,139（5）:1519 - 1535 .

［24］ Zheng X,W u G,Zhang S,et al. Using analysis state to construct a forecast error covariance matrix in ensemble Kalman filter assimilation［J］. Advances in Atmospheric Sciences,2013,30（5）:1303 - 1312 .

［25］ Shu Y,Zhu J,W ang D,et al. Assimilating remote sensing and in situ observationsinto a coastal model of northern South China Sea using ensemble Kalman filter［J］. Continental Shelf Research,2011,31（6）:S24 - S36 .

［26］ H unt B R,Kostelich E J,Szunyogh I . Efficient data assimilation for spatiotemporal chaos:A local ensemble transform Kalman filter［J］. Physica D:Nonlinear Phenomena,2007,230（1）:112 - 126 .

［27］ Elowerdew J . Towards a theory of optimallocalisation［J］. Tellus A,2015,67,25257 .

［28］ Perianez A,Reich H,Potthast R . Optimallocalization for ensemble Kalman filter systems［J］.気象集誌第2辑,2014,92（6）:585 - 597 .

［29］ H outekamer P L,Mitchell H L,Pellerin G,et al. Atmospheric data assimilation with an ensemble Kalman filter:Results with real observations ［J］. M onthly W eather Review,2005,133（3）:604 - 620 .

［30］ Buehner M ,Charette C,He B,et al.Intercomparison of 4-D Var and En K E systems for operational deterministic N W P［R］. W W RP/T H O RPE X W orkshop on 4 D-VA R and Ensemble Kalman Eilter Intercomparisons . Buenos Aires,2008 .

［31］ Samuelsen A,Bertino L,Hansen C .Impact of data assimilation of physical variables on the spring bloom from T O P A Z operational runs in the North Atlantic［J］. Ocean Science,2009,5（4）:635 - 647 .

［32］ Chassignet E P,H urlburt H E,M etzger E J,et al. U .S . G O D A E:Global Ocean Prediction With the H Ybrid Coordinate Ocean M odel（H Y C O M）［J］. Oceanography,2009,22（2）:64 - 75 .

［33］ Bocquet M ,Pires C A,W u L . Beyond gaussian statistical modeling in geophysical data assimilation［J］. M onthly W eather Review,2010,138（8）: 2997 - 3023 .

［34］ Han X,Li X . An evaluation of the nonlinear/non-Gaussian filters for the sequential data assimilation［J］. Remote Sensing of Environ ment,2008, 112（4）:1434 - 1449 .

［35］ Van Leeuwen P J . A variance-minimizing filter for large-scale applications［J］. M onthly W eather Review,2003,131（9）:2071 - 2084 .

［36］ Van Leeuwen P J . Particle filtering in geophysical systems［J］. M onthly W eather Review,2009,137（12）:4089 - 4114 .

［37］ Ham mersley J M ,Handscomb D C . M onte carlo methods［M］. London:M ethuen Publishing,1964 .

［38］ Gordon N J,Salmond D J,S mith A E . Novel approach to nonlinear/non-Gaussian Bayesian state estimation［J］. Proceedings of the IEEE,1993, 140（2）:107 - 113 .

［39］ Capp O,Godsill S J,M oulines E . An overview of existing methods and recent advances in sequential M onte Carlo［J］. Proceedings of the IEEE, 2007,95（5）:899 - 924 .

［40］ Douc R,Capp O . Comparison of resampling schemes for particle filtering［C］//Proceedings of the 4th International Symposiu m on Image and Signal Processing and Analysis,ISP A05 . Zagreb,Criatia,2005:64 - 69 .

［41］ Kotecha J H,Djuric P M . Gaussian su m particle filtering［J］.Signal Processing,IEEE Transactions on,2003,51（10）:2602 - 2612 .

［42］ Kotecha J H,Djuric P M . Gaussian particle filtering［J］.Signal Processing,IEEE Transactions on,2003,51（10）:2592 - 2601 .

［43］ Xiong X,Navon I M ,Uzunoglu B . A note on the particle filter with posterior Gaussian resampling［J］. Tellus A,2006,58（4）:456 - 460 .

［44］ Nakano S,Ueno G,Higuchi T . M erging particle filter for sequential data assimilation［J］. Nonlinear Processesin Geophysics,2007,14（4）:395 -408 .

［45］ Snyder C,Bengtsson T,Bickel P,et al. Obstacles to high-dimensional particle filtering［J］. M onthly W eather Review,2008,136（12）:4629 -4640 .

［46］ Dau m E,H uang J . Curse of dimensionality and particle filters［C］// Proceedings of the Aerospace Conference,IEEE . Newport,2003 .

［47］ Snyder C .Particlefilters,the“optimal”proposaland high-dimensionalsystems［C］//Proceedings ofthe EC M W E Seminar on Data Assimilation for Atmosphere and Ocean,2011 .

［48］ Diard J,Bessiere P,M azer E . A survey of probabilistic models using the bayesian program ming methodology as a unifying framework［C］//The Second International Conference on Computational Intelligence,Robotics and Autonomous Systems . Erance,2003 .

［49］ 李新,摆玉龙.顺序数据同化的Bayes滤波框架［J］.地球科学进展,2010,25（5）:515 - 522 . Li Xin,Ba Yulong . A Bayesian filter framework for sequential data assimilation［J］. Advances in Earth Science,2010,25（5）:515 - 522 .

［50］ Chen Z . Bayesian filtering:Erom Kalman filters to particle filters,and beyond［J］.Statistics,2003,182（1）:1 - 69 .

［51］ H outekamer P L,Mitchell H L . A sequential ensemble Kalman filter for atmospheric data assimilation［J］. M onthly W eather Review,2001,129 （1）:123 - 137 .

［52］ Tang Y,A mbandan J,Chen D . Nonlinear measurement function in the ensemble Kalman filter［J］. Advances in Atmospheric Sciences,2014,31 （3）:551 - 558 .

［53］ Yang C,Min J,Tang Y .Evaluation oftwo modified Kalman gain algorith msfor radar data assimilation in the W R E model［J］. Tellus A,2015,67, 25950.

［54］ Crisan D,Doucet A . A survey of convergence results on particle filtering methods for practitioners［J］.Signal Processing,IEEE Transactions on, 2002,50（3）:736 - 746 .

［55］ Le Gland E,M onbet V,Tran V - D .Large sample asymptoticsforthe ensemble Kalman filter［M］//Crisan D . The Oxford Handbook of Nonlinear Eiltering . Oxford:Oxford U niversity Press,2009:598 - 634 .

［56］ Anderson J L . Ensemble Kalman filters for large geophysical applications［J］. Control Systems,IEEE,2009,29（3）:66 - 82 .

［57］ Lorenz E N . Deterministic nonperiodic flow［J］.Journal of the Atmospheric Sciences,1963,20（2）:130 - 141 .

［58］ Lorenz E N . Predictability:A problem partly solved［C］// Proceedings of the Seminar on Predictability . U K,1996 .

［59］ M orzfeld M ,Tu X,Atkins E,et al. A random map implementation ofimplicitfilters［J］.Journal of Computational Physics,2012,231（4）:2049 -2066 .

［60］ Doucet A,Godsill S,Andrieu C . On sequential M onte Carlo sampling methods for Bayesian filtering［J］. Statistics and Computing,2000,10（3）: 197 - 208 .

［61］ Papadakis N,M Min E,Cuzol A,et al. Data assimilation with the weighted ensemble Kalman filter［J］. Tellus A,2010,62（5）:673 - 697 .

［62］ Beyou S,Cuzol A,Gorthi S S,et al. W eighted ensemble transform kalman filter for image assimilation［J］. Tellus A,2013,65,18803 .

［63］ Nakano S Y . H ybrid algorith m of ensemble transform and importance sampling for assimilation of non-Gaussian observations［J］. Tellus A,2014, 66 .

［64］ Erei M ,Kunsch H R . Bridging the ensemble Kalman and particle filters［J］. Biometrika,2013,100（4）:781 - 800 .

［65］ Shen Z,Tang Y . A modified ensemble Kalman particle filter for non-Gaussian systems with nonlinear measurement functions［J］.Journal of Advances in M odeling Earth Systems,2015,7（1）:50 - 66 .

［66］ Van Leeuwen P J . Nonlinear data assimilation in geosciences:an extremely efficient particle filter［J］. Quarterly Journal ofthe Royal M eteorological Society,2010,136（653）:1991 - 1999 .

［67］ Ades M ,Van Leeuwen P J . An exploration of the equivalent weights particle filter［J］. Quarterly Journal of the Royal M eteorological Society, 2013,139（672）:820 - 840 .

［68］ Ades M ,Van Leeuwen P J . The equivalent-weights particle filterin a high-dimensional system［J］. Quarterly Journal of the Royal M eteorological Society,2015,141（687）:484 - 503 .

［69］ Chorin A J,M orzfeld M ,Tu X .Implicit particle filters for data assimilation［J］. Com municationsin Applied M athematics and Computational Science,2010,5（2）:221 - 240 .

［70］ Luo X,H oteit I . Efficient particle filtering through residual nudging［J］. Quarterly Journal of the Royal M eteorological Society,2014,140（679）: 557 - 572 .

［71］ 万莉颖.集合同化方法在太平洋海洋高度计资料同化中的应用研究［D］.北京:中国科学院大气物理研究所,2006 . W an Liying . Ensemble methods and applications to altimetry data assimilation in the Pacific［D］. Beijing:Institute of Atmospheric Physics,Chinese Academy of Science,2006 .

［72］ Deng Z,Tang Y . The retrospective prediction of E NSO from 1881 to 2000 by a hybrid coupled model:（Ⅱ）Interdecadal and decadal variationsin predictability［J］.Climate dynamics,2009,32（2/3）:415 - 428 .

［73］ Haugen V E,Evensen G . Assimilation of SL A and SST data into an O G C M for the Indian Ocean［J］. Ocean Dynamics,2002,52（3）:133 - 151 .

［74］ Arulampalam M S,M askell S,Gordon N,et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking［J］. Signal Processing,IEEE Transactions on,2002,50（2）:174 - 188 .

附录1:从贝叶斯公式推导卡尔曼滤波器

在贝叶斯滤波理论中,状态场的更新公式由贝叶斯定理给出:

式中,xk|y1:k- 1表示tk时间先验的状态变量（预报）,我们假设其满足均值为xfk,协方差为Pf的多元高斯分布。同时,假设观测误差满足均值为0,协方差为R的高斯分布,即

式中,d和m分别为状态空间和观测空间的维数。代入式（A1）,并在等式两边取对数得到

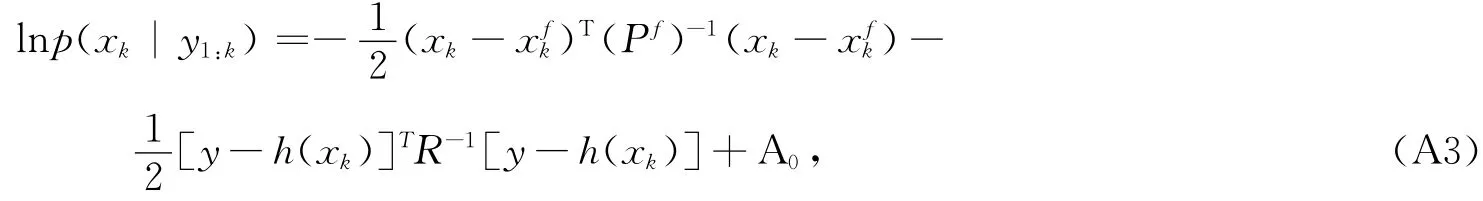
式中,A0是一个常数。

因此可以得到目标函数

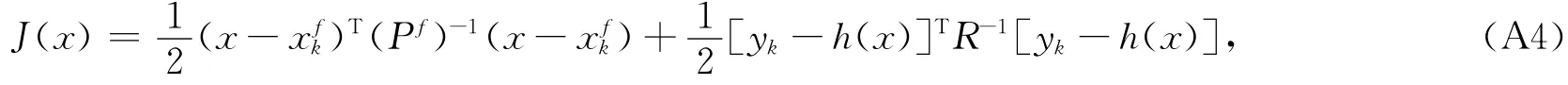
通过最小化J（xk）可以使得后验概率分布密度最大,在后验概率分布密度函数为高斯分布的假定下这也相当于使后验分布的协方差最小。容易发现,式（A4）和从最佳线性无偏估计得到的三维变分的目标函数完全一致。

如果模式的观测算子为线性的函数H ,不妨假设后验状态场（分析）是预报和观测的线性组合

为简化记号,我们这里忽略了时间下标k。根据预报误差协方差和观测误差协方差的定义,可知

为使Pa最小,令

式中,trace代表矩阵的迹。可以解出

公式（A6）和（A7）是经典的卡尔曼滤波器中的状态场更新公式和协方差更新公式。而式（A9）则是卡尔曼增益矩阵的解析表达式。

附录2:加权集合卡尔曼滤波器算法流程

（1）应用集合卡尔曼滤波器将观测yk同化到预报集合中,得到分析集合并估算其协方差矩阵

其中

（3）应用标准的重取样算法［74］:对于粒子每个,根据其权重大小计算重取样指标s（i）,得到所有的重取样指标之后,再令,i = 1,…,N。举例来说,图1中根据权重计算的重取样指标为｛4,4,5,5,5,5,6, 6,6,7｝,意味着根据权重,前3个和最后3个粒子全部删去,中间的第4到第7个粒子分别重复2、4、3、1份。具体求重取样指标的多种算法可参考相关文献［38］,重取样后的粒子集合｛,i = 1,…,N｝再次变成等权重的。

然后就可以用这个等权重的粒子集合来积分模式,进入下一个“预报-分析”循环。

原论文中假设观测算子H是线性的,实际上即使观测算子是非线性的函数h ,我们只需要将加权集合卡尔曼滤波器按照第3.1节中集合卡尔曼滤波器的方法进行一定的扩展就可以拓展其适用范围。

中图分类号:P731

文献标志码:A

文章编号:0253-4193（2016）03-0001-14

收稿日期:2015-05-24；

修订日期:2015-08-07。

基金项目:国家自然科学基金项目（41276029,41321004）；科技部国家基础科研项目（2013CB430302）；卫星海洋环境动力学国家重点实验室自主课题（SO E DZZ1404,SO E DZZ1518）。

作者简介:沈浙奇（1984—）,男,浙江省杭州市人,博士,从事数据同化方法的研究。E-mail:zqshen @ sio .org .cn

*通信作者:唐佑民,男,教授,研究员,主要从事大尺度海气相互作用、可预报性理论、数据同化、E NSO和气候预测等方面的研究。E-mail:ytang @ unbc .ca

沈浙奇,唐佑民,高艳秋.集合资料同化方法的理论框架及其在海洋资料同化的研究展望［J］.海洋学报,2016,38（3）:1 - 14,doi: 10.3969/j.issn .0253-4193.2016.03.001

Shen Zheqi,Tang Youmin,Gao Yanqiu . The theoreticalframework of the ensemble-based data assimilation method and its prospect in oceanic data assimilation［J］. Haiyang Xuebao,2016,38（3）:1 - 14,doi:10.3969/j.issn .0253-4193.2016.03.001

The theoretical framework of the ensemble-based data assimilation method and its prospectin oceanic data assimilation

Shen Zheqi1,Tang You min1,2,Gao Yanqiu1
（1 .State Key Laboratory of Satellite Ocean Environment Dynamics,Second Institute of Oceanography,State Oceanic Administration,Hangzhou 310012,China；2 .EnvironmentalScience and Engineering,University of Northern British Columbia,Prince George V2 N 4Z9,Canada）

Abstract:In the nu mericalsimulation ofthe ocean dynamic system,data assimilation is able to use thelimited observation data and nu merical modelto best estimate the ocean state,and effectively reduce the uncertainty from theinitial conditions . Therefore,data assimilation plays an important role in the study of modern physical oceanography . The ensemble Kalman filter（En K E）is an effective data assimilation method,which has attracted broad attention in oceanic data assimilation since it is proposed about twenty years ago .In recent years,the particle filter（PE）has become a hot research field,foritis not restricted by the linear and Gaussian assu mption of the model. This paper analyzes and su m marizes the current theories about the En K E and PE,in the framework of Bayesian filtering theory . The En K E and PE algorith ms are proposed and compared . On this basis,we further discuss the major obstacle for applying the particle filter in oceanic data assimilaiton at present. Some feasible solutions are also introduced . This paper is expected to provide theoretical basis for further develop ment and application of the ensemble-based data assimilation method in oceanic data assimilation .

Key words:data assimilation；ensemble Kalman filter；particle filter；non-Gaussian noise；Bayesian filter