叶片轴向进气的离心叶轮设计及分析
2016-04-18耿文倩但汉攀陈聪聪李景银
耿文倩, 但汉攀, 陈聪聪, 李景银
(1. 西安交通大学 能源与动力工程学院, 西安 710049; 2. 杭州汽轮机股份有限公司, 杭州 310012)
叶片轴向进气的离心叶轮设计及分析
耿文倩1,但汉攀2,陈聪聪1,李景银1
(1. 西安交通大学 能源与动力工程学院, 西安 710049; 2. 杭州汽轮机股份有限公司, 杭州 310012)
摘要:研究了位于叶轮0截面叶片轴向进气的离心叶轮气动设计方法和规律.采用四阶三次Bezier曲线生成叶轮子午流道型线,通过分段多项式函数给定叶片在轮盘和轮盖面上的角动量,并针对叶片轴向进气离心叶轮,提出了叶轮进口相对直径的修正公式,研究了其叶片安装角的分布规律.结果表明:轴向进气叶轮叶片安装角分布规律与径向进气叶轮的叶片安装角不同,其叶片安装角基本按单调方式增加;由叶轮进口相对直径修正公式计算后,在工况范围内的全压多变效率可以提高5%左右.
关键词:离心叶轮; 叶片轴向进气; 叶轮进口相对直径; 叶片安装角
目前,离心压缩机使用范围广泛,有关气流是径向和斜向进气的三元叶轮的研究很多[1-2],也比较系统.如徐忠等[3]研究了气流径向进气的离心叶轮叶片进口相对直径的确定方法,按照叶片进口处相对速度最小的原则推导得到相应的公式,并进行了验证.Dixon等[4]也是按进口相对速度最小原则来确定离心叶轮进口相对直径,但该文中的公式对叶片进口阻塞系数、加速系数以及叶轮进口直径D0和叶片进口直径D1不等的情况等均未考虑,也没有明确指出所推导的公式是适合轴向进气还是径向进气.席光等[5]对径向和斜向进气的三元叶轮的叶片安装角进行了分析,发现其沿流线的分布规律为单驼峰曲线.张莉[6]研究了叶片设计规律,得出一种比较合理的叶片表面角动量及其导数沿流道的分布规律.
相对而言,研究气流轴向进气离心叶轮的文献较少.但随着高压大流量离心叶轮的发展,越来越多的离心叶轮采用叶片轴向进气方式(即叶片起始于叶轮的0截面),如LSCC叶轮[7]和Krain叶轮[8].因此,有必要对叶片轴向和径向进气的离心叶轮主要结构参数的确定和三元叶片的变化规律进行对比研究.
笔者以某台大流量高压比离心叶轮为例,对叶片轴向进气的离心叶轮进口相对直径的确定方法、三元叶片的气动设计方法和叶片安装角的规律进行了研究.
1子午面形状的设计
1.1叶轮基本参数
叶轮叶片采用轴向进气,即叶片进口边位于叶轮的0截面,为直线且与叶轮转轴垂直.气动设计参数如下:介质为空气,质量流量为22 kg/s,进口总温为293.05 K,进口总压为98 kPa,总压比为2.01.其一元结构尺寸和转速等参数按一元设计方法[3]确定,获得叶轮的进出口结构尺寸R1S、R1H、R2及叶轮出口宽度B2.子午面出口收缩角θ按经验值范围选取.轮盘、轮盖曲线均由四阶三次Bezier曲线控制生成,如图1所示.
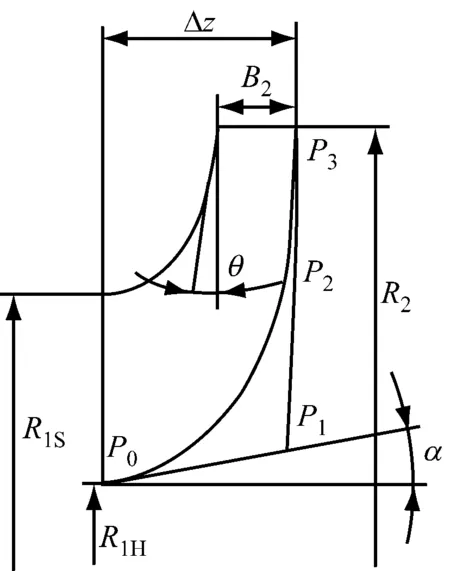
图1 叶轮子午流道参数化造型
1.2轮盘轮盖型线确定
定义(zi,ri)为控制点Pi(i=0,1,2,3)的坐标.4个控制点中P3点坐标已知,给定叶轮轴向宽度Δz后,P0点坐标也可确定.已知叶轮子午面轮廓线在叶片进出口处的倾角,则P1和P2点只可在轮廓线端点的切线方向移动,则控制变量减为2个.如再次给定叶轮出口子午面轮廓线的曲率ρe,则根据四阶三次Bezier曲线控制方程及其端点性质,可以建立P1和P2点的关系如下:
(1)
因此,就只剩下1个自由变量r2.通过改变r2即可控制轮盘和轮盖型线.一般情况下,当型线的最大曲率取得极小值时,叶轮有较高的效率.当轮盘最大曲率较大时,可通过增大叶轮轴向宽度Δz来减小最大曲率.
2三元叶片的气动设计
采用“全可控涡”[9]思想对离心叶轮进行准三维气动设计,得到三元扭曲叶片.“全可控涡”即通过给定和控制叶片表面角动量(rVθ)的分布以控制叶轮内的流场来设计叶轮.
王尚锦[10]采用5阶多项式函数来分段给定叶片表面角动量分布,其假定叶片出口滑移区的角动量为常数,但这种假定的合理性并未得到验证.因此,笔者采用最高4阶的分段多项式函数来给定角动量的分布,且未限制叶片出口角动量为常数,在保证精度的同时,方便了角动量的控制和简化计算.图2为叶轮子午面分区示意图.
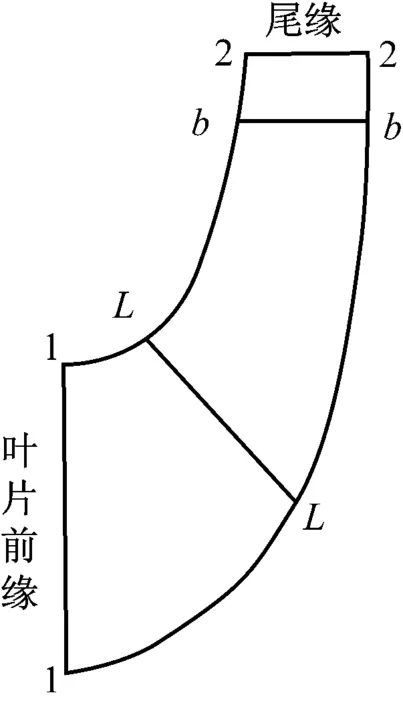
图2 叶轮子午面分区示意图
在叶片进口附近过渡区(1-L),叶片表面角动量分布的幂函数表达式为:

(2)
在叶道中间区(L-b),叶片表面角动量则采用2次幂函数(抛弧线)给定,表达式如下:
(3)
在叶轮出口附近滑移区(b-2),叶片表面角动量分布表达式为:
(4)
式中:m为子午面流线相对长度,取值0~1.
分离半径(即b点的半径)rb由Stanitz公式确定:
(5)
式中:Z为叶片数;τ2为叶轮出口阻塞系数.
通过上述分段函数给定叶片表面角动量,同时假定叶片进口无预旋和气流冲击,则叶片进口有(rVθ)1=0,d(rVθ)/dm=0,且要求d2(rVθ)/dm2=0;叶片出口处角动量满足Kutta条件,即d(rVθ)/dm=0.为保证叶片表面角动量分布曲线连续光滑,要求分段曲线在点L、b处的一阶导数均相等.通过调节点L处(rVθ)L、d(rVθ)/dm和点b处(rVθ)b的大小,可调整叶片的加载方式.
离心叶轮出口角动量的取值一般是叶顶大于叶根,这有利于抑制叶轮出口气流的不均匀性.一元设计最终确定叶片出口(rVθ)2=99.98,所以取叶根(rVθ)2H=98,叶顶(rVθ)2S=103.由于后加载叶片流场较均匀,不易发生分离[11],所以通过调整叶片加载方式为后加载来获得高效叶轮.最终得到叶根、叶顶的角动量及角动量变化率,沿轮盘、轮盖流线的分布曲线如图3和图4所示.
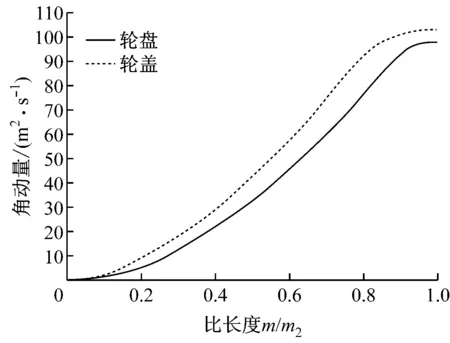
图3 角动量沿轮盘、轮盖流线的分布
3叶轮进口相对直径对性能的影响
文献[3]介绍了2种叶轮进口相对直径D1/D2(D2为叶轮出口直径)的确定方法:
(1) 根据叶片进口处相对速度最小原则确定的计算公式:
(6)

图4 角动量变化率沿轮盘、轮盖流线的分布
式中:d为轮毂直径;Kv1、Kv2分别为叶片进、出口比容比;τ1为叶轮进口阻塞系数;φ2r为流量系数;Kc=c1rτ1/c0,其中c1r为叶片进口处绝对速度的径向分速度,c0为叶轮进口处绝对速度.
(2) 对半开式离心叶轮诱导轮的直径比的经验公式:
(7)
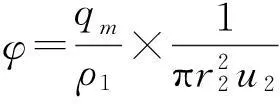
对于这2种叶轮进口相对直径的确定方法,当设计参数相同时,方法(1)计算得到的D1/D2值小于方法(2)计算所得值.方法(2)中的经验公式是为计算具有导风轮的半开式离心叶轮的D1/D2而提出的.为了比较这2种方法所得到的D1/D2对叶片轴向进气离心叶轮性能的影响,并确定D1/D2的最佳取值范围,对比设计了4个不同D1/D2的叶轮,分别为叶轮A、叶轮B、叶轮C和叶轮D,其中叶轮A和叶轮D的D1/D2分别采用上述2种方法计算,叶轮B和叶轮C的D1/D2通过插值圆整得到.为突出D1/D2对叶轮的影响,对4个叶轮子午流道形状的设计作如下要求:保证叶片进口宽度基本一致,其他主要结构尺寸相同;保证叶轮出口子午面出口收缩角θ相同以及轮盖转弯处最大曲率基本一致.
不同D1/D2对应的三元离心叶轮的子午面几何特征参数见表1.其他参数不变,叶片表面气流角动量分布按图3和图4给定,即角动量及其变化率沿流线比长度分布保持一致.对表1中的4个离心叶轮进行三元气动设计,模拟分析这4个三元离心叶轮的气动性能,计算结果见图5.
由图5可知,随着叶轮进口相对直径D1/D2的增大,在小质量流量区域,叶轮全压多变效率降低,在大质量流量区域,叶轮全压多变效率先随着D1/D2的增大而提高,但当D1/D2达到一定值后,继续增大D1/D2,叶轮全压多变效率反而下降了.在工况范围内,与叶轮A和叶轮D相比,叶轮B和叶轮C的全压多变效率提高5%左右.

表1 各三元叶轮子午面几何特征参数

(a) 全压多变效率
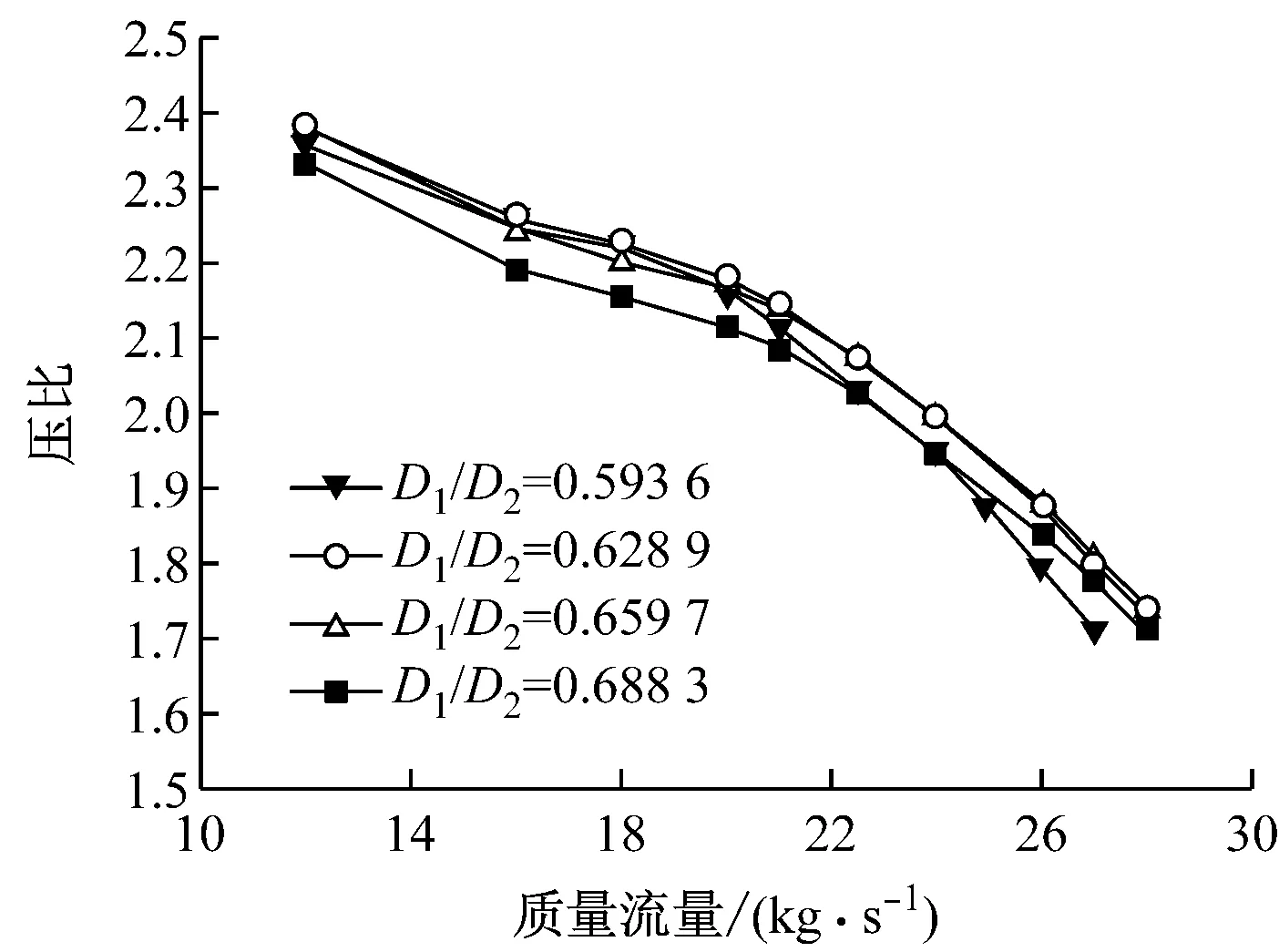
(b) 压比
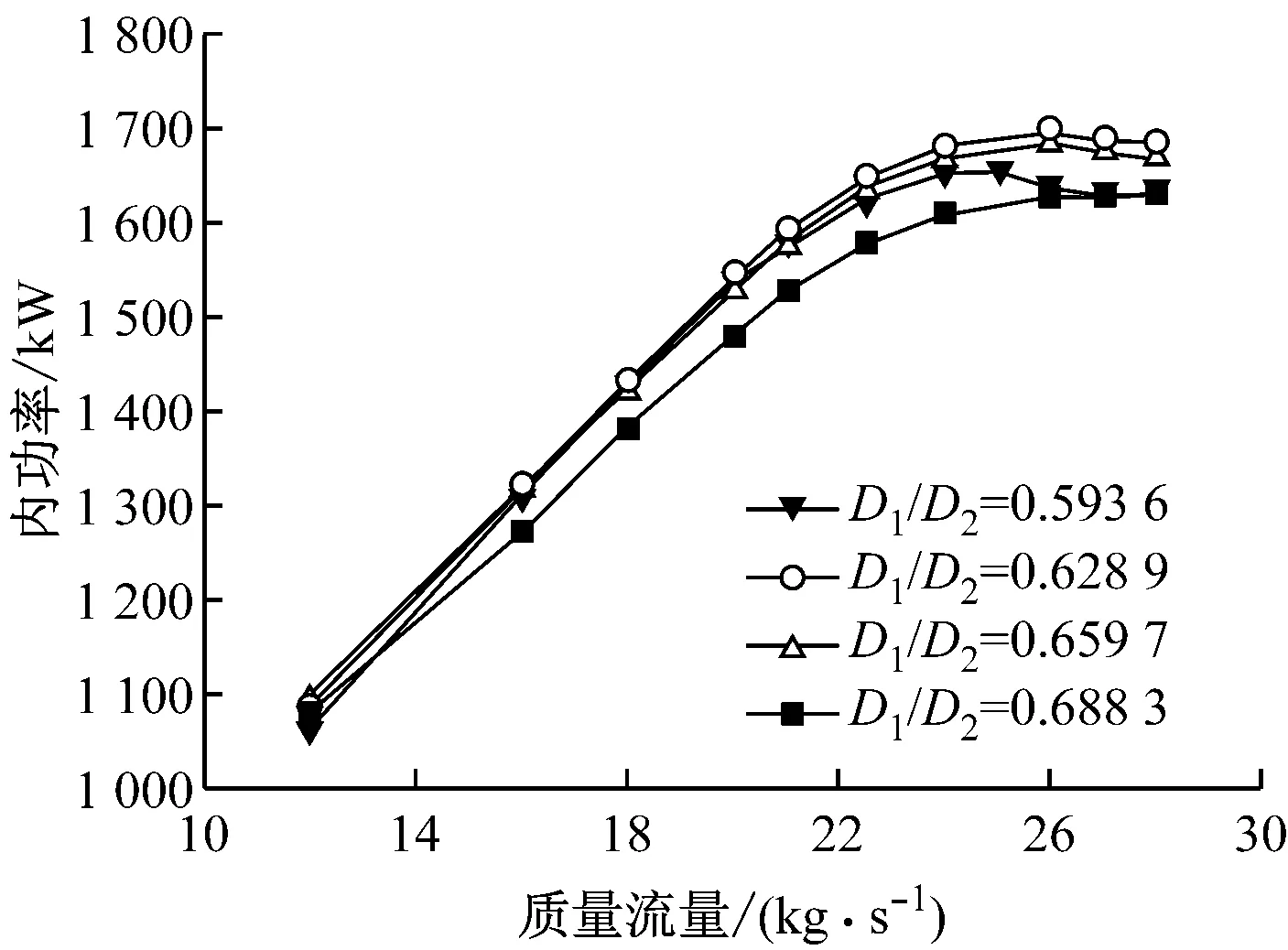
(c) 内功率
当D1/D2由0.593 6增大到0.628 9(约为叶轮A的1.06倍)时,大质量流量区域效率提高尤为明显,在1.2倍设计质量流量(27 kg/s)下,全压多变效率提高约4.9%,小质量流量区域效率则有所下降,但没大质量流量区域变化明显,只下降约0.3%.当D1/D2提高到0.659 7(约为叶轮A的1.11倍)时,小质量流量区域效率继续下降,约降低0.7%,但内功率和压比基本不变,设计点质量流量区域和大质量流量区域的全压多变效率继续提高,但趋势变缓,在1.2倍设计质量流量点(27 kg/s),全压多变效率再次提高1.4%;当D1/D2增大到0.688 3(由式(7)计算确定)时,叶道明显变短,叶轮做功能力降低,效率也降低了,叶轮排气压比有较为明显的下降.
由于所设计的三元叶轮在主流区的流动情况都较为良好,因而选取叶轮C和叶轮D的0.9倍叶高处的流动情况进行对比(见图6).由图6可知,在0.9倍叶高处,叶轮D的低速区明显大于叶轮C的低速区.
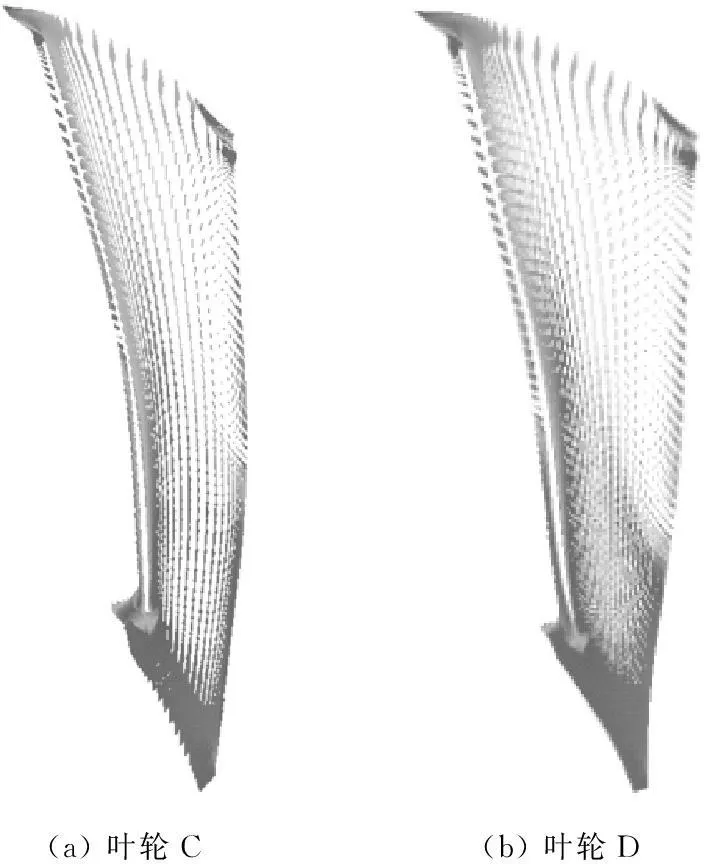
(a)叶轮C(b)叶轮D
图60.9倍叶高处叶轮C和叶轮D的相对速度矢量图
Fig.6Distribution of relative velocity vectors of blade C and
blade D at 90% blade height
综上所述,式(6)和式(7)计算得到的D1/D2值之间存在一个最优值.对于叶轮叶片进口为轴向进气的离心叶轮,建议对上述2种确定方法进行修正:
(1) 根据叶片进口处相对速度最小原则可得:
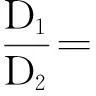
(8)
(2) 根据经验公式可得:
(9)
以叶轮C为例,其叶片几何特性分析见图7和图8.图7为叶片轴向进气三元扭曲叶片叶根、叶顶型线在回转平面上的投影.由于叶片是轴向进气,且叶片进口内、外径跨度大,所以叶片进口的角度变化较大.图8给出了叶根和叶顶的叶片安装角沿轮盘、轮盖流线的分布规律.由图8可知,设计得到的高效叶轮叶顶叶片安装角基本上是单调增大的,没有出现驼峰现象,这个变化趋势与文献[5]总结的一般径向和斜向进气离心叶轮的叶片安装角分布规律有所不同;叶根的叶片安装角基本上还是出现了单驼峰现象,与文献[5]类似.

图7 叶根、叶顶型线在回转面上的投影

图8 叶根和叶顶的叶片安装角沿轮盘、轮盖流线的分布
4结论
(1) 采用最高为4阶的分段多项式函数来给定叶片表面角动量,在保证精度的同时计算更为方便,且能较好地控制叶片轴向进气叶轮内流场,设计得到高效的大流量、中高压比离心叶轮.
(2) 针对叶片轴向进气离心叶轮,提出了叶轮进口相对直径的修正公式.由进口相对直径修正公式计算得到的叶轮比由原始计算公式(6)和式(7)计算得到的叶轮,在工况范围内的全压多变效率提高5%左右.
(3) 叶片轴向进气叶轮中,三元扭曲叶片的叶片安装角的分布规律与一般径向或斜向进气叶轮不同.因此,建议采用给定角动量的气动控制方法设计叶片轴向进气离心叶轮.
参考文献:
[1]BONAIUTI D, ZANGENEH M. On the coupling of inverse design and optimization techniques for turbomachinery blade design[C]//ASME Turbo Expo 2006: Power for Land, Sea, and Air. Barcelona,Spain:ASME,2006:1431-1444.
[2]卢金铃,席光,祁大同,等.离心泵三元扭曲叶片设计的研究[J].工程热物理学报,2002,23(增刊): 61-64.
LU Jinling,XI Guang,QI Datong,etal. Research on the inverse design method for 3-d blades in centrifugal pumps[J].Journal of Engineering Thermophysics,2002,23(S): 61-64.
[3]徐忠.离心压缩机原理[M].北京:机械工业出版社,1990:71-81.
[4]DIXON S L, HALL C A. Fluid mechanics and thermodynamics of turbomachinery[M].6th ed. Oxford:Butterworth-Heinemannm Elsevier Ltd,2010:229-236.
[5]席光, 王志恒,王尚锦. 叶轮机械气动优化设计中的近似模型方法及其应用[J].西安交通大学学报,2007,41(2): 125-135.
XI Guang,WANG Zhiheng,WANG Shangjin. Aerodynamic optimization design of turbomachinery with approximation model method[J].Journal of Xi'an Jiaotong University,2007, 41(2):125-135.
[6]张莉.离心叶轮的准三元正命题分析与基于平均S_2 m流面的半反命题设计的研究[D].西安:西安交通大学,1996.
[7]HATHAWAY M D, CHRISS R M, STRAZISAR A J,etal. Laser anemometer measurements of the three- dimensional rotor flow field in the NASA low-speed centriufugal compressor[R]. Washington D C,USA:NASA, 1995.
[8]KRAIN H, HOFFMAN W. Verification of an impeller design by laser measurement and 3D-viscous flow calculation[R].New York,USA:ASME, 1989.
[9]张莉,徐忠.离心叶轮的半反命题设计[J].上海电力学院学报,1998, 14(1):1-6.
ZHANG Li, XU Zhong. Study on qusai-inverse proposition on mean S2-streamsurface in centrifugal impeller[J].Journal of Shanghai Institute of Electric Power,1998,14(1): 1-6.
[10]王尚锦.离心压缩机三元流动理论及应用[M].西安:西安交通大学出版社,1991: 55-147.
[11]马广健.基于控制载荷法的离心风机单板叶片设计与内部流场分析[D].上海:上海交通大学,2011.
Design and Analysis of a Centrifugal Impeller with Blade Leading Edge Located at the Impeller Eye
GENGWenqian1,DANHanpan2,CHENCongcong1,LIJingyin1
(1. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China;2. Hangzhou Steam Turbine Co., Ltd., Hangzhou 310012, China)
Abstract:The design of an impeller with axial admission of air flows, i.e., the impeller with blade leading edge located at the impeller eye, was presented and discussed. First, the cubic Bezier curve was applied to design the meridional flow channel. Then, the distribution of the angular momentum on surfaces of the shroud and hub was prescribed by using a piecewise polynomial function. Finally, modified formulas for the optimum ratio of D1/D2 (D0=D1) were proposed via numerical simulations for the impeller with blade leading edge at the impeller eye, and simultaneously the blade angle was analyzed. Results show that the blade angel on the shroud surface shows a monotonic increasing tendency for the impeller with axial admission of air flows, different from that with radial admission of air flows. By calculation with above modified formulas to optimize the ratio of D1/D2, the whole-pressure polytropic efficiency can be improved by 5% within the scope of working conditions.
Key words:centrifugal impeller; blade axial admission; ratio of D1/D2; blade angle
文章编号:1674-7607(2016)02-0113-05
中图分类号:TK16
文献标志码:A学科分类号:470.30
作者简介:耿文倩(1992-),女,河南商丘人,硕士研究生,研究方向为三元离心压缩机的设计.电话(Tel.):18629356249;E-mail:gengwq@stu.xjtu.edu.cn.
基金项目:国家自然科学基金资助项目(51276137)
收稿日期:2015-01-29
修订日期:2015-05-26
