核电厂主蒸汽管道材料断裂韧性试验三维数值模拟研究

张　旭，　窦一康,2，　梁兵兵

(1．上海核工程研究设计院，上海 200233； 2．上海发电设备成套设计研究院，上海 200240)



核电厂主蒸汽管道材料断裂韧性试验三维数值模拟研究

张旭1，窦一康1,2，梁兵兵1

(1．上海核工程研究设计院，上海 200233； 2．上海发电设备成套设计研究院，上海 200240)

摘要：基于商用软件ABAQUS对国产化主蒸汽管道材料P11合金钢的断裂韧性试验中起裂前的加载过程进行了精细的三维数值模拟，对含侧槽和光滑侧面2种标准CT试样结构进行建模分析，获得加载过程中裂纹前沿的塑性区、应力场和J积分的三维精细分布及变化规律.开展了SA335 P11合金钢材料含侧槽结构试样的断裂韧性试验，试验中载荷线位移响应曲线与有限元分析结果具有很好的一致性，验证了数值分析的有效性.通过有限元和试验相结合的方式，确定了延性金属材料试样采用光滑侧面结构是导致其试验过程中难以起裂的主要原因，含侧槽结构试样能为裂纹尖端提供有效约束，使得裂纹前沿附近区域的塑性区尺寸、局部J积分和张开应力分布更加均匀，对优化延性金属材料断裂韧性试验作用明显.

关键词：国产化P11合金钢； 有限元三维模拟； 断裂韧性试验； 侧槽结构； 应力应变场

在试验过程中，随着载荷的施加，延性金属材料的初始预制疲劳裂纹在起裂前首先发生钝化，同时随着载荷增加，在光滑侧面标准CT试样的自由表面会出现明显的塑性流动，给试验造成较大困难，为了限制这种塑性流动，通常采取试样侧面加工侧槽结构.这种结构的改变会对裂纹前沿附近的塑性区尺寸、应力场和局部J积分等参数带来明显影响，进而对试验结果造成影响.显然，量化分析延性金属材料裂纹前沿的主要断裂力学参数的分布与变化规律，对于优化试验方案和获得可靠试验结果都尤为重要，故需开展精细的三维有限元分析.笔者基于弹塑性断裂力学理论，采用有限元分析方法对标准CT试样的含侧槽和光滑侧面2种结构进行了三维建模分析，对2种结构中裂纹前沿的塑性变形和断裂力学相关参数进行精细对比分析.

1有限元分析过程

基于平面应变(PE)和平面应力(PS)2种应力状态的二维分析相结合的方法可整体估算试验过程中的力学响应，同时可节省计算时间，故获得了广泛应用，但是二维分析未纳入试样结构的三维效应影响，无法获得精细的局部状态参数.随着计算能力的不断提高和对断裂问题面外约束等方面理论的深入研究，三维数值模拟因分析的准确性受到越来越广泛的应用[3-7].笔者基于ABAQUS /Standard分析建立三维模型，使用等效积分区域法计算J积分模块，对2种不同结构试样裂纹前沿进行有限元分析.为了准确模拟计算加载过程中裂纹前沿的应力应变场，采用Mises屈服准则和J2流动理论，即各向同性硬化定律，采用更接近材料真实力学响应的塑性增量理论建立本构方程，对裂纹前沿进行非线性力学分析,主要研究起裂前裂纹前沿参数的变化，不涉及裂纹扩展相关问题.

1.1材料性能

管道材料为国产SA335-P11合金钢，在280 ℃下进行拉伸性能试验，测得弹性模量E为180 GPa，泊松比ν为0.29，屈服强度σy为230 MPa，拉伸强度σu为480 MPa，故流动应力σY为355 MPa.分析获得P11合金钢材料的真应力应变曲线(图1)，作为进行有限元分析的材料参数输入.

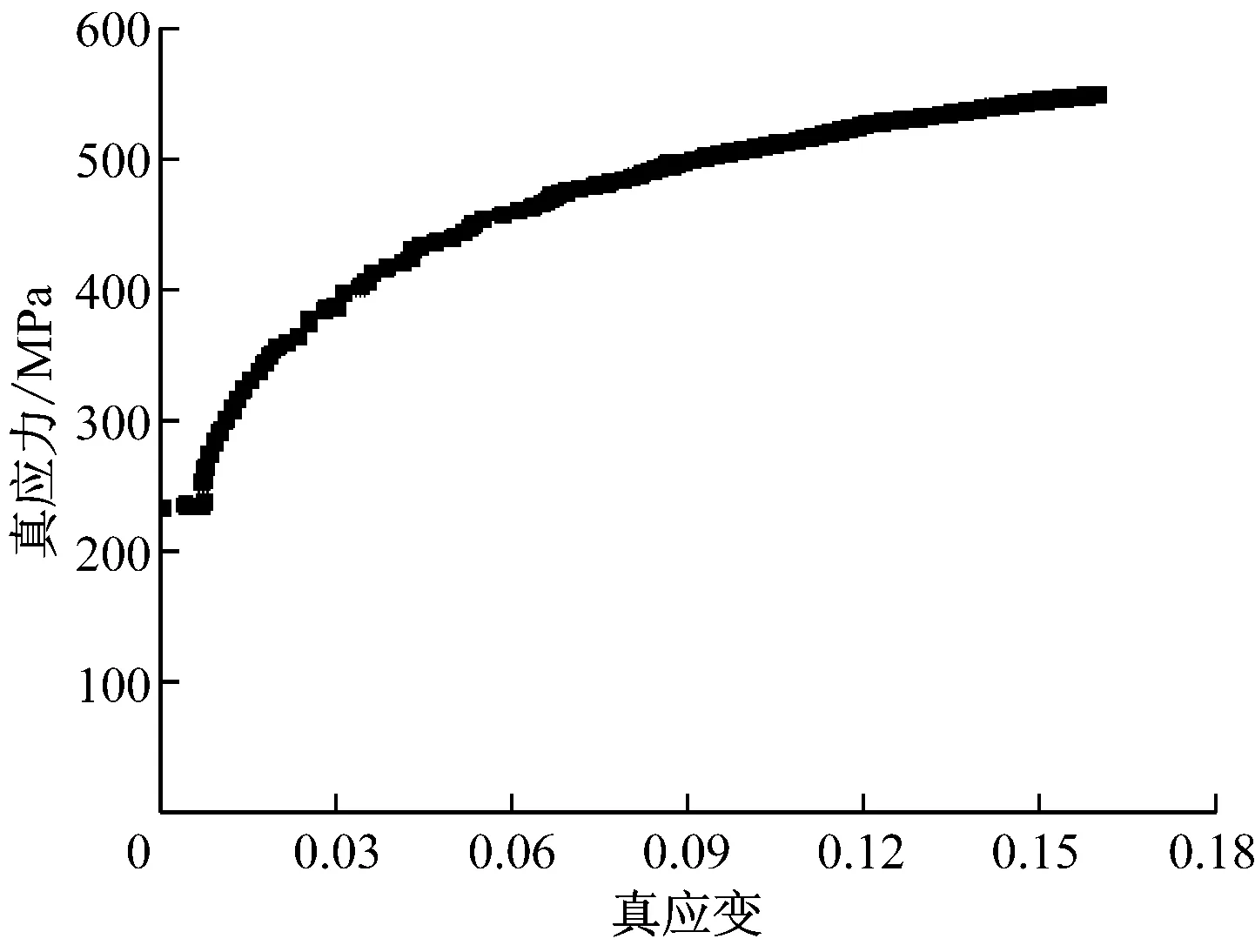
图1　P11合金钢的真应力应变曲线

1.2几何结构模型

图2所示为本文中主要考虑的2种CT试样结构，即表面光滑的试样和含侧槽结构的试样.为了满足试验有效性要求，取允许的最大管道试样厚度40 mm CT试样,主要参数为厚度B=40 mm，宽度W=80 mm，高度H=86 mm，初始裂纹长度(含疲劳裂纹)为40 mm，初始裂纹占比a/W=0.5，其中含侧槽结构的试样两侧各加工深度为4 mm的侧槽，试样净厚度BN=32 mm.

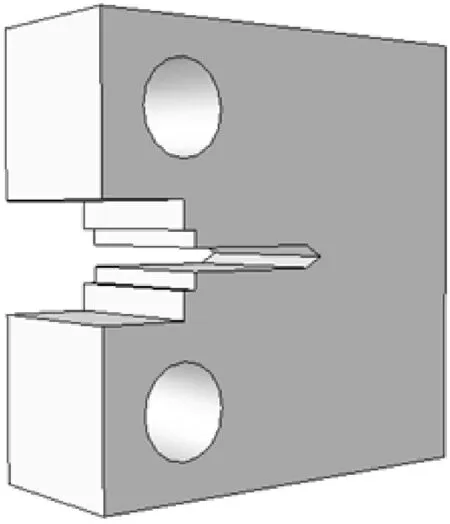
(a) 光滑侧面结构试样

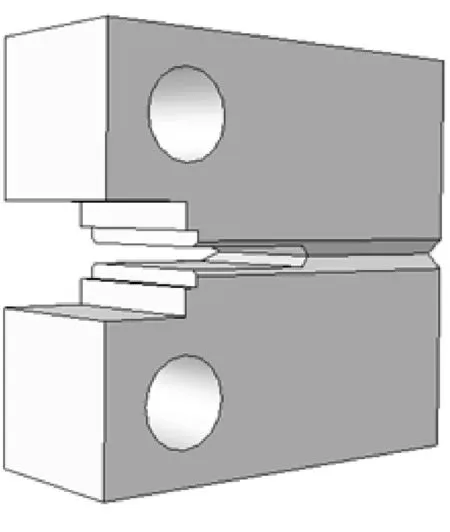
(b) 含侧槽结构试样

1.3边界条件与网格结构

由于试样结构和载荷具有对称性，建立1/4模型进行有限元分析.试验边界条件参照实际情况，在对称约束基础上，采用分析刚体模型(analytic rigid)进行接触分析来模拟加载过程，采用位移控制方式对试样进行I型加载，对刚体施加向上位移约束，位移为0.75 mm.为了计算J积分值，定义裂纹前沿和裂纹扩展方向，如图3所示，采用等效积分区域法分析，通过ABAQUS内嵌程序计算局部J积分.

由于裂纹尖端应力应变梯度大，需要进行网格的局部加密，采用围线结构，如图3(b)所示；由于自由表面附近存在明显的应力梯度，故在厚度方向上进行了从表面到中间面网格由密向疏过渡设计，如图3(a)所示；含侧槽结构试样的网格更为复杂，侧槽附近的网格结构如图3(c)所示.光滑侧面结构试样的网格划分方案与含侧槽结构裂纹面部分一致.

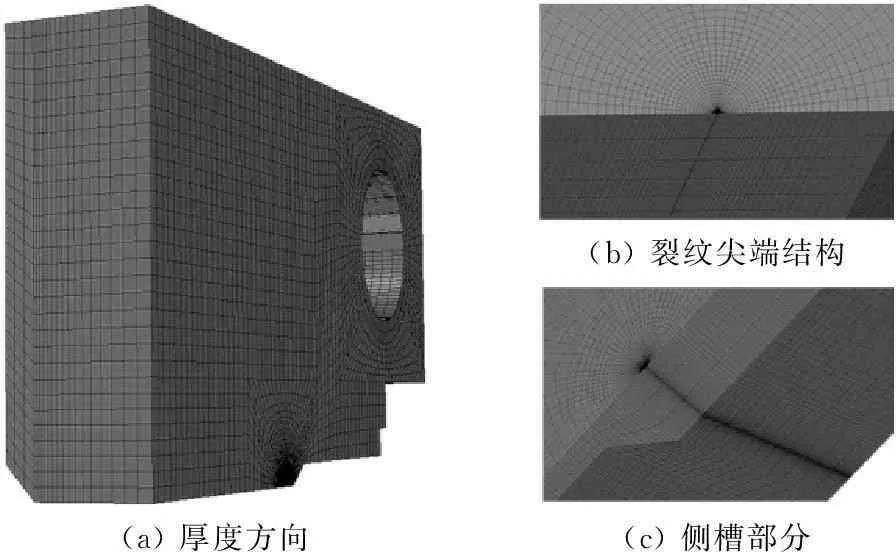
(a)厚度方向(b)裂纹尖端结构(c)侧槽部分

图3网格设计

Fig.3Design of the finite element mesh

网格采用可满足裂纹尖端分析精度要求的六面体单元C3D8R，单元在裂纹尖端退化为三棱柱结构.在裂纹尖端向外沿径向环绕40圈围线进行积分运算获得J积分，环向设计了32个分区，裂纹尖端最小单元尺寸为径向0.003 mm，环向0.001 mm.含侧槽结构和光滑侧面结构试样厚度方向分别有17层和21层单元，含侧槽结构和光滑侧面结构试样所含单元总数分别为62 211个和67 734个.网格敏感性分析表明本结构能够满足分析需求.

1.4输出结果及分析

使用ABAQUS 6.12对上述2组模型进行非线性力学计算，输出围线对应区域裂纹尖端的局部J积分.为了避免塑性增量理论引起的J积分计算路径影响，采用外圈J积分计算结果，并将厚度方向上不同位置的J积分取平均值，用以模拟试验测试结果，见文献[8].基于接触分析模拟加载过程,可以输出接触力，用以模拟实际施加载荷.选择载荷线上两节点输出相对位移变化，用以模拟实际COD引伸计测量的载荷线位移VLLD(Load-Line Displacement).同时，精密的网格结构可保证计算输出裂纹前沿附近的塑性区、张开应力场，用于实际分析，获得载荷P、载荷线位移VLLD、裂纹前沿局部J积分、裂纹前沿局部应力应变和位移场后，通过对比分析即可确定2种结构在试验过程中对试验结果造成影响的根本原因.

2分析结果的试验论证

为了验证有限元分析的有效性，从某国产主蒸汽管道上切取LC方向(即试样上裂纹方向为管道环向)1.6T-CT试样进行试验.试样结构参照ASTM E1820—2009标准,当试样预制完疲劳裂纹后，在两侧面分别加工深度为试样厚度10%的侧槽，试样初始裂纹长度占比为a0/W=0.5，获得的试验过程中载荷线位移曲线如图4所示.

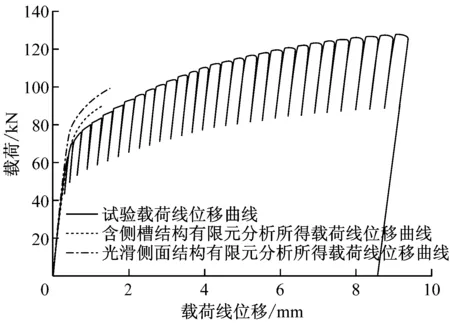
图4　载荷线位移曲线验证分析

将2种模型有限元分析输出的载荷线位移曲线与试验结果对比可知，含侧槽结构有限元分析结果与试验结果具有高吻合度，由于试验中出现卸载释放能量，故数值模拟结果略高于试验结果，光滑侧面结构有限元分析结果高于含侧槽结构有限元分析结果.对比结果一方面验证了有限元分析的有效性，另一方面也证明本文模型可在材料断裂韧性试验中辅助进行载荷水平、载荷线位移响应行为等方面的预估，为优化试验提供支持.

3裂纹前沿参数对比分析

通过对含侧槽结构和光滑侧面结构CT试样模型的有限元分析,获得2种结构试样在不同载荷水平下的裂纹前沿附近不同位置的断裂参数分布和变化规律，其中主要分析与裂纹前沿塑性区尺寸相关的裂纹尖端的Mises应力、对I型裂纹起主要影响的垂直于裂纹面的主应力σyy和加载过程中的J积分.为了同时对裂纹前沿参数沿厚度的分布规律和随载荷增加的变化规律进行研究，提取裂纹前沿厚度方向不同位置处、不同载荷水平下各节点的力学参数进行对比分析.

3.1裂纹前沿塑性区分布规律

模型选用Mises屈服准则，故由Mises屈服应力水平和范围可确定裂纹前沿附近发生屈服的程度和范围，分析不同结构模型在试验过程中裂纹前沿塑性区的分布.在载荷线位移为VLLD=1.4 mm时，2种结构模型在裂纹前沿附近的Mises等效应力场如图5所示.

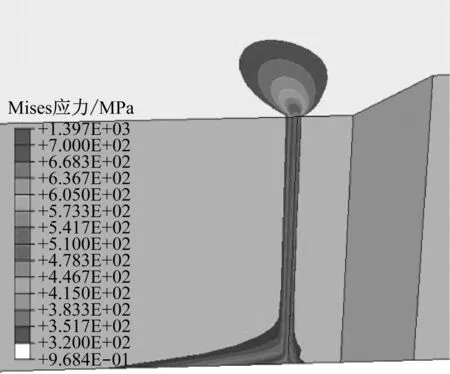
(a) 含侧槽结构

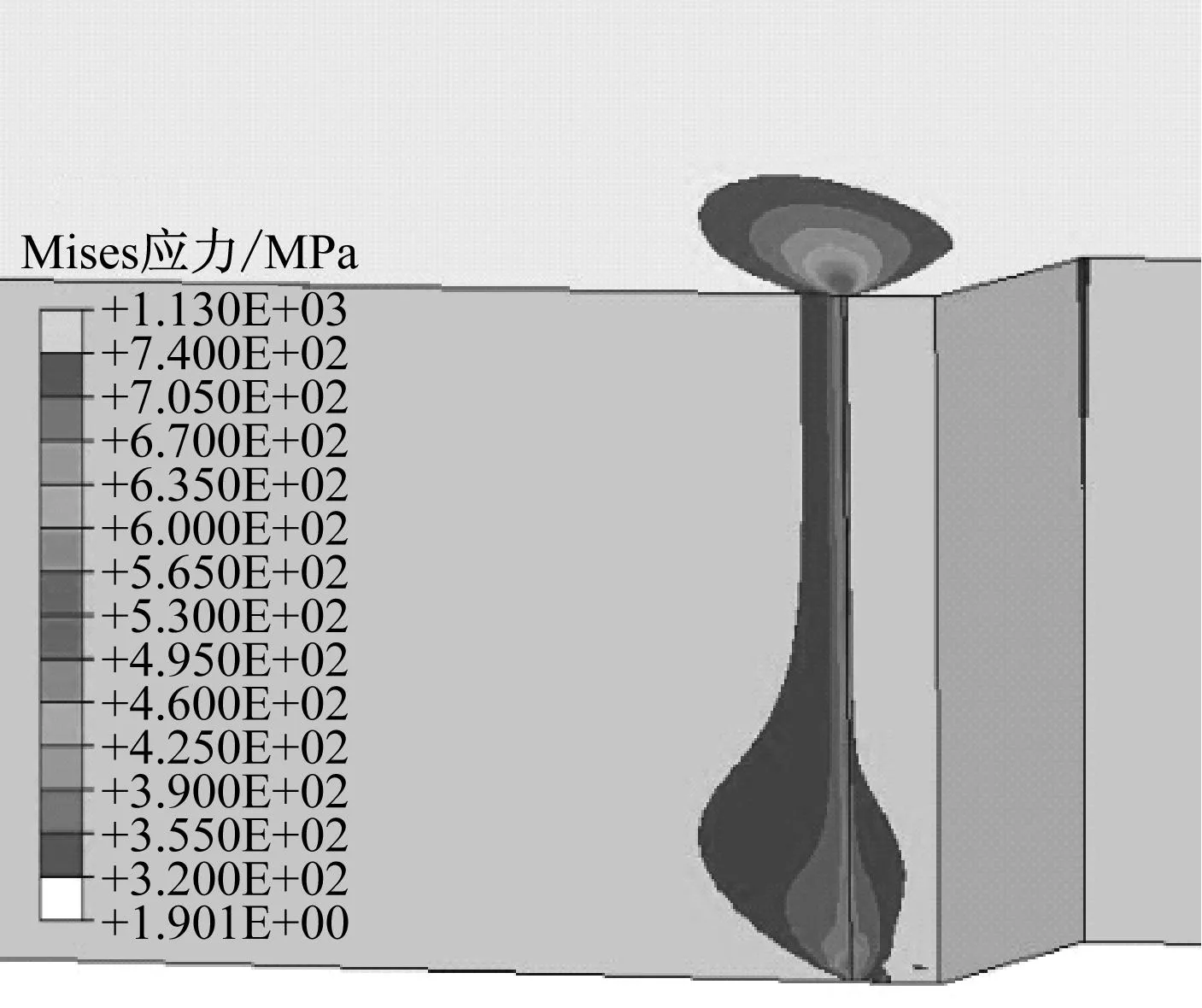
(b) 光滑侧面结构

在含侧槽结构模型的裂纹前沿与侧槽相交的位置，由于侧槽根部应力集中和裂纹尖端的应力奇异性叠加,导致试验自由表面出现高应力梯度，塑性区几何尺寸远高于其他位置，屈服范围也较大，但在厚度方向上占比10%左右，裂纹前沿绝大部分的应力参数接近中间面，分布均匀一致，其中均匀部分在中间面的应力水平最高，如图5(a)所示.光滑侧面结构模型裂纹前沿在自由表面附近的应力也出现应力梯度，塑性区尺寸分布表现为由低向高再向低的规律，接近中间面时趋于均匀，其中塑性区尺寸较大的区域相对裂纹前沿尺寸占比接近30%.

由相同载荷水平下2种结构模型的Mises应力分布云图对比可知，含侧槽结构引起裂纹前沿塑性区的重新分布，裂纹前沿塑性区尺寸分布更加均匀；光滑侧面结构模型中，自由表面附近塑性区变化范围大，使得材料在厚度方向一定距离内丧失约束，出现自由塑性流动，增加了试验难度.

3.2裂纹前沿张开应力分量分布规律

裂纹前沿的张开应力分量(即模型中试样裂纹面上y向应力分量σyy)是影响I型裂纹开裂的主要原因，故σyy的水平直接反映了裂纹前沿受到张开载荷的强度.图6给出了载荷线位移VLLD=1.4 mm时2种结构模型裂纹前沿的y向正应力σyy沿试样厚度方向的分布规律.

含侧槽结构模型的张开应力在靠近侧槽位置较大，由侧槽向中间面的变化则呈现出先减小再平缓增大的趋势，在中间位置附近趋于稳定，且应力水平整体均匀，如图6(a)所示.光滑侧面结构模型的张开应力则呈现出从自由表面向中间面逐步增大的趋势，自由表面张开应力小，中间面张开应力最大，张开应力值分布不均匀，如图6(b)所示.

对比分析结果，在相同载荷水平下，含侧槽结构模型整个裂纹前沿受力均匀集中，更有利于裂纹起裂和平直扩展；光滑侧面结构模型中的裂纹前沿张开应力分布不均匀,直接影响厚度方向上裂纹扩展量分布，并导致表面附近优先出现塑性变形，替代开裂，给试验有效性造成严重干扰.

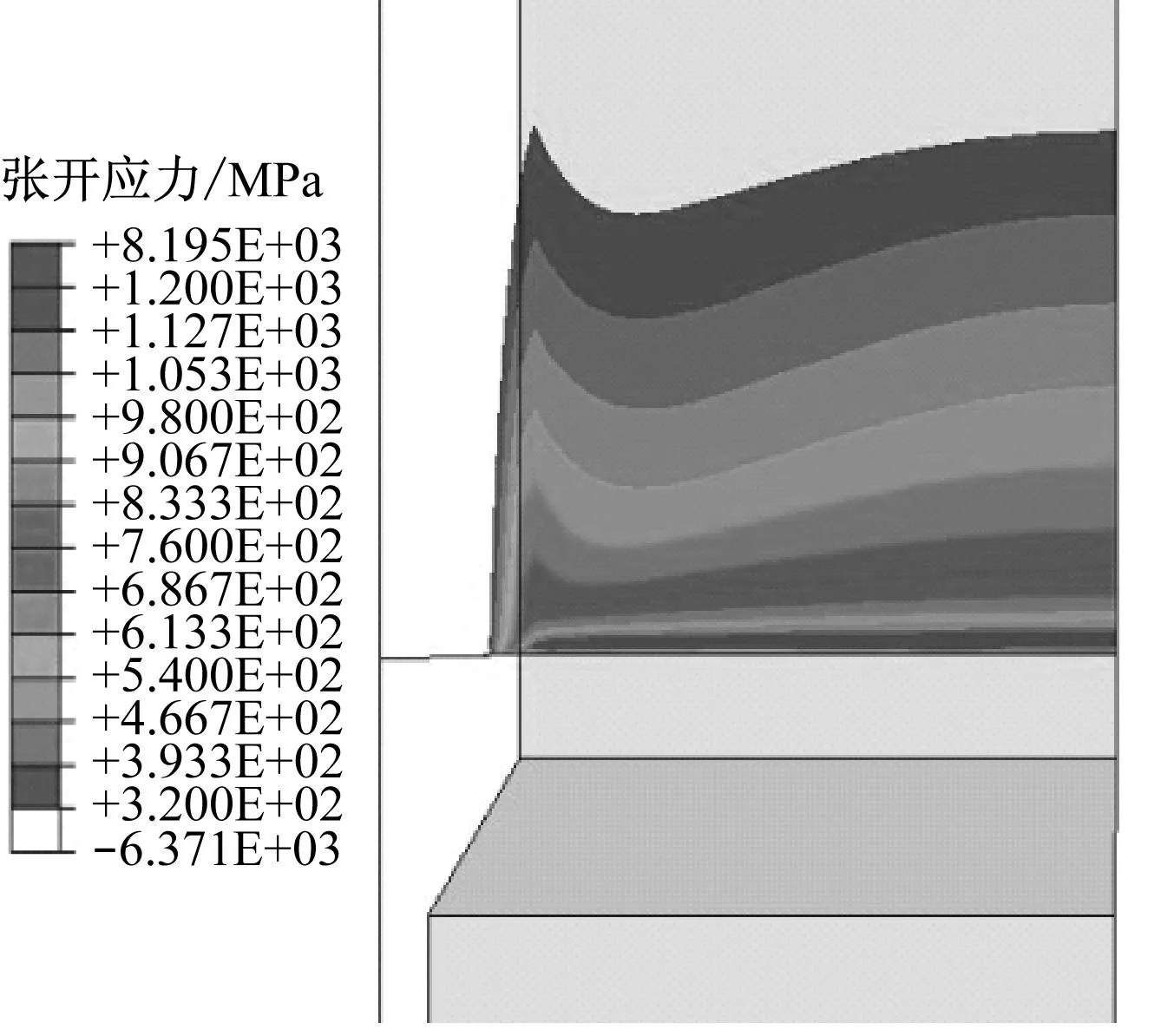
(a) 含侧槽结构

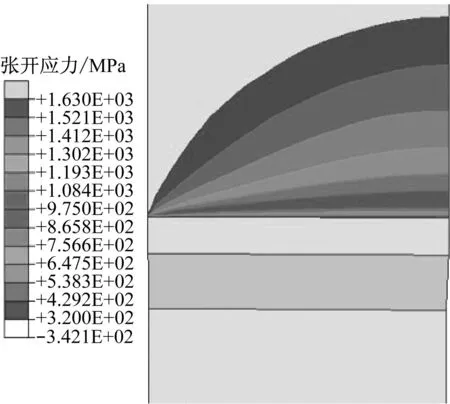
(b) 光滑侧面结构

3.3裂纹前沿附近J积分分布及变化规律

对2种结构模型输出的沿裂纹前沿的J积分进行分析，含侧槽结构模型裂纹前沿J积分分布如图7(a)所示，图中BN为含侧槽结构试样在断裂处的净厚度；光滑侧面结构模型裂纹前沿J积分分布如图7(b)所示，其中2z/B=0处为中间面，2z/B=1处为外侧面，B为光滑侧面结构试样在断裂处的厚度.

对比图7(a)和图7(b)可知，随着载荷线位移的不断增加，裂纹前沿各个部位J积分均逐步增大，其中含侧槽结构模型沿厚度方向局部J积分分布均匀统一，在侧槽面与裂纹面交接处J积分会出现突增但占比较小，而光滑侧面结构模型沿厚度方向局部J积分出现中间面大、自由表面小的分布，且两者差别随着载荷线位移的增加而增大.

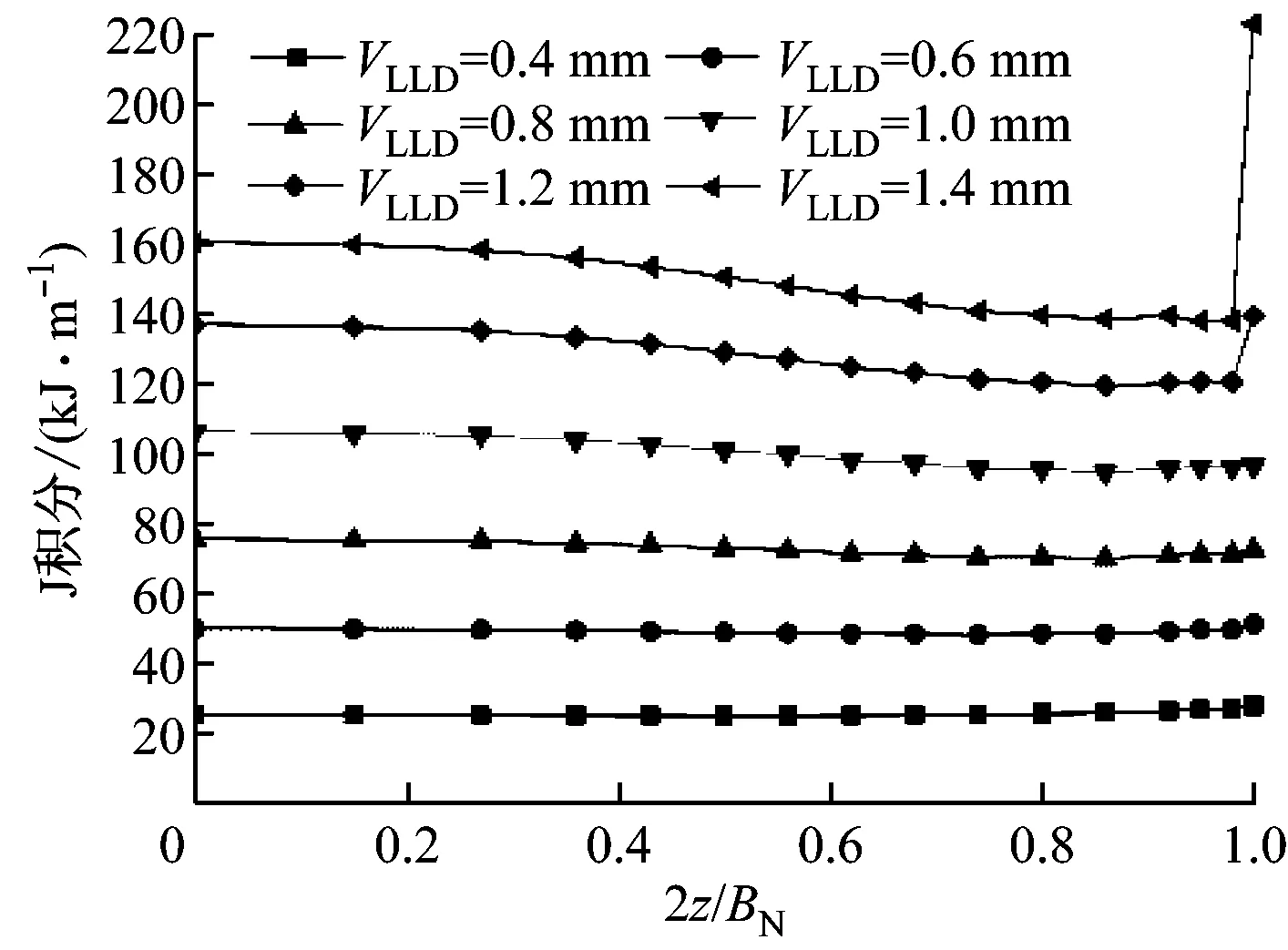
(a) 含侧槽结构

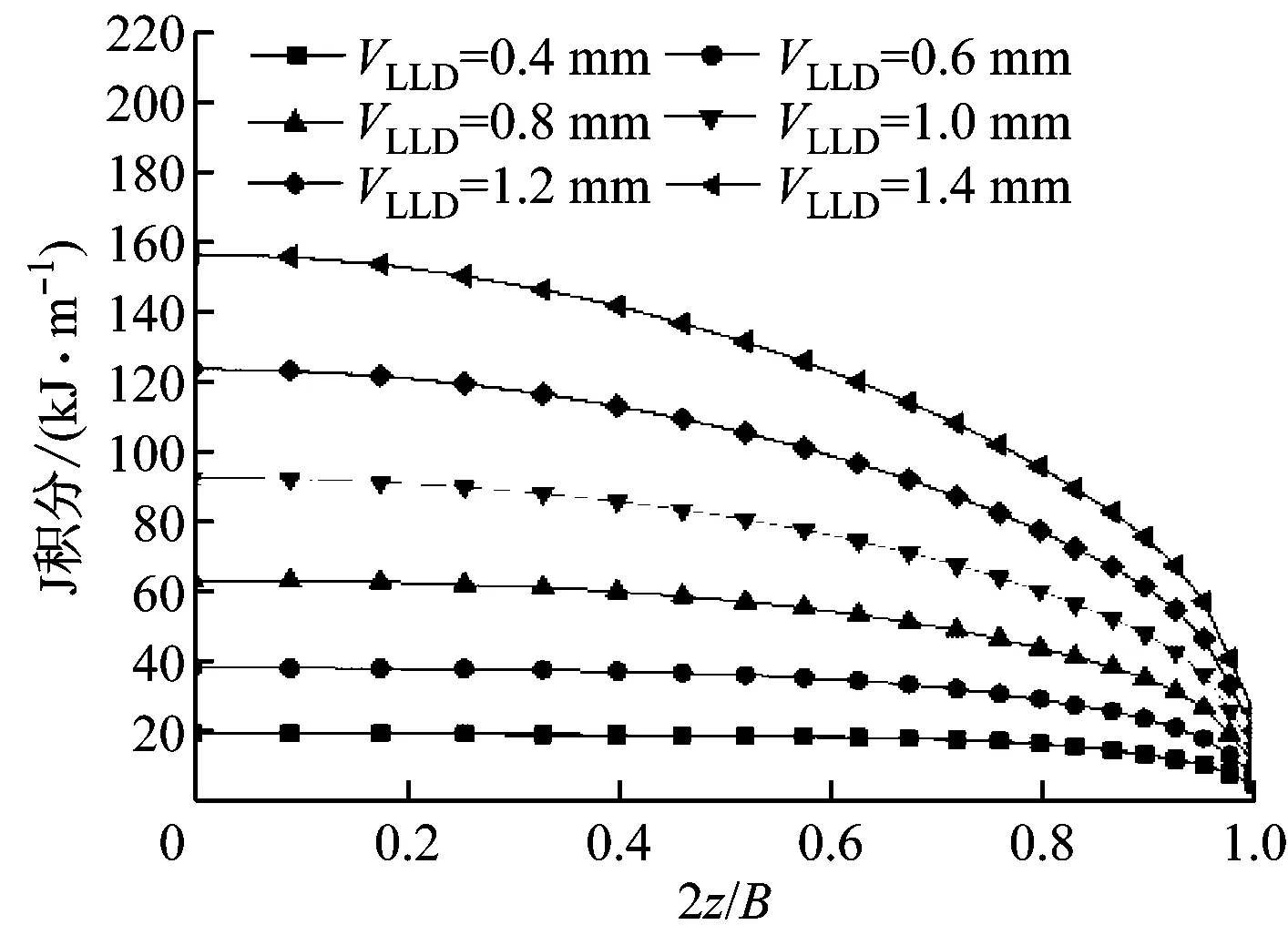
(b) 光滑侧面结构

Fig.7Distribution and variation of local J integrals for both the specimens

对比可知，在相同载荷线位移下，含侧槽结构模型和光滑侧面结构模型中间面的J积分水平相当，裂纹前沿J积分最大，但含侧槽结构模型的平均J积分水平高于光滑侧面结构模型，即在相同载荷线位移下，含侧槽结构模型裂纹前沿扩展驱动力更大，这对于延性金属材料的断裂是有利的.

综上分析可知，对于延性金属材料，为了限制试样自由表面的塑性流动，保证裂纹平直扩展，确保裂纹前沿处于有效约束状态，试样采用含侧槽结构是更加合理的选择；光滑侧面结构试样存在自由表面约束效应小，起裂难度大，裂纹扩展不易控制等问题，故应首先选择含侧槽结构试样开展相关试验.

4结论

(1) 基于有限元分析方法获得的载荷线位移曲线与试验结果相符，是可靠有效的，可用于试验过程中载荷的分析.

(2) 获得了2种结构模型裂纹前沿的塑性区尺寸、张开应力和J积分在加载过程中沿厚度方向的三维分布规律，即含侧槽结构将引起裂纹前沿各参数的重新分布，除了在侧槽根部位置出现小范围应力集中外，所有参数分布更加均匀一致，同时试验过程中裂纹前沿力学参数更加趋近于平面应变状态，使得试验更加优化.

(3) 含侧槽结构引起裂纹前沿附近应力场的重新分布，使裂纹前沿各断裂参数更加趋于均匀，提高了裂纹前沿附近材料的约束能力，在相同载荷线位移下，含侧槽结构可增大裂纹扩展的驱动力，故含侧槽结构试样更适用于延性金属材料的断裂韧性试验.

(4) 试验过程中光滑侧面结构试样在加载过程中自由表面附近张开应力水平偏低是难以起裂的主要原因.

参考文献：

[1]张振,胡正飞,范立坤,等. 国产P92钢低周疲劳性能与断裂特征研究[J]. 动力工程学报,2014,34(4):330-336.

ZHANG Zhen, HU Zhengfei, FAN Likun,etal. Low cycle fatigue and fracture properties of domestic P92 heat-resistant steels[J]. Journal of Chinese Society of Power Engineering, 2014,34(4):330-336.

[2]ASTM E1820—2009. Standard test method for measurement of fracture toughness[S]. USA: American Society for Testing and Materials,2010.

[3]SAXENA S, RAMAKRISHNAN N, DUTTA B K. Determination of stretch zone width using fem[J]. Engineering Fracture Mechanics, 2009, 76(7): 911-920.

[4]GRABA M, GALKIEWICZ J. Influence of the crack tip model on results of the finite elements method[J]. Journal of Theoretical and Applied Mechanics, 2007, 45(2): 225-237.

[5]KULKA R S, SHERRY A H. Fracture toughness evaluation in C(T) specimens with reduced out-of-plane constraint[C]//ASME 2012 Pressure Vessels and Piping Conference.Toronto,Canada: American Society of Mechanical Engineers, 2012.

[6]TKACH Y, BURDEKIN F M. A three-dimensional analysis of fracture mechanics test pieces of different geometries-Part 1 stress-state ahead of the crack tip[J]. International Journal of Pressure Vessels and Piping, 2012, 93/94(5): 42-50.

[7]SHLYANNIKOV V N, BOYCHENKO N V, TUMANOV A V,etal. The elastic and plastic constraint parameters for three-dimensional problems[J]. Engineering Fracture Mechanics, 2014, 127: 83-96.

[8]BROCKS W, SCHEIDER I, GEESTHACHT G F. Numerical aspects of the path-dependence of the J-integral in incremental plasticity[R]. Geesthacht, Germany: GKSS Forschungszentrum, 2001.

Three-dimensional Numerical Investigation on Fracture Toughness Testing of SA335 P11 Alloy Steel for PWR Main Steam Piping

ZHANGXu1,DOUYikang1,2,LIANGBingbing1

(1.Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China;2. Shanghai Power Equipment Research Institute, Shanghai 200240, China)

Abstract：Using commercial software ABAUQS, a detailed three-dimensional finite element analysis was conducted to the loading process before breaking of SA335 P11 alloy steel for PWR main steam piping during fracture toughness test, so as to numerically analyze the toughness of standard CT specimens with and without side grooves, and to obtain the distribution and variation law of the plastic zone, stress field and local J integrals around the crack front. Meanwhile, a fracture toughness test was carried out to P11 alloy steel specimens with side grooves, and the load-displacement curves agreed well with those of finite element analysis, proving the numerical method to be effective. Based on both the finite element analysis and experimental tests, it has been found that for testing of ductile metals, the specimen with plane-sided structure is hard to get cracking, and the structure with side groove is believed to be a better choice, as it keeps providing high level of constraints around crack front, which makes the distribution of plastic zone dimension, local J integrals and the opening stress become more uniform, and therefore helps to optimize relevant test procedures.

Key words：localized P11 alloy steel; 3D finite element analysis; fracture toughness test; side-groove structure; stress-strain field第二代压水堆核电厂主蒸汽管道通常采用碳钢， P11合金钢抵抗二回路流动加速腐蚀的能力相对一般碳钢材料具有明显优势，故被用于第三代压水堆核电厂AP1000的主蒸汽管道材料.国产主蒸汽管道应用破前泄漏(LBB)技术时,需要材料在电厂运行温度下的非常规力学试验参数(如J-R阻力曲线、疲劳性能曲线[1]等)作为输入.故需依据ASTM E1820—2009《Standard Test Method for Measurement of Fracture Toughness》标准[2]开展运行温度环境下的准静态断裂韧性试验.

文章编号：1674-7607(2016)01-0074-05

中图分类号：TL353

文献标志码：A学科分类号：430.20

作者简介：张旭 (1989-)，男，湖北十堰人，硕士研究生，主要从事反应堆结构力学方面的研究.电话(Tel．)：15121103421；

收稿日期：2015-04-13

修订日期：2015-05-11

E-mail：zhangxu2@snerdi.com.cn．