遗传算法在炸药爆轰参数计算中的应用*

谢中元,王晓峰,王 浩,周 霖

(1.西安近代化学研究所,陕西 西安 710065；2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

遗传算法在炸药爆轰参数计算中的应用*

谢中元1,王晓峰1,王 浩1,周 霖2

(1.西安近代化学研究所,陕西 西安 710065；2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

为解决爆轰参数计算中自变量取值范围要求严格以及收敛性差等问题，在最小自由能法的基础上，引入遗传算法建立了炸药爆轰参数的计算方法，并利用典型单质炸药和混合炸药的实验结果对计算结果进行了验证。结果表明：采用该方法计算得到的单质和混合炸药的爆速、爆压与实验测试结果基本一致，误差在5%以内，满足炸药性能预估的要求；该方法人工干预弱，只需一次性确定少数主要组分物质的量的变化范围，可适应于多配方优化计算。

爆炸力学;遗传算法;最小自由能法;爆轰参数

爆轰参数理论计算是炸药性能预估的技术基础，是炸药技术的核心内容。炸药爆轰参数计算方法的研究一直受到重视，从C.L.Mader[1]推广应用的BKW状态方程，到Qiu Jianbin等[2]、李德华等[3]采用的WCA状态方程，再到Wu Xiong[4]、吴雄等[5]提出的VLW状态方程，爆轰参数的计算范围和计算精度等均得到明显改善。然而这类方法在爆轰产物组分含量的处理中大多采用B-W准则[6]、泰勒级数展开法[7]或简化平衡常数法[8]，以致计算过程中存在一定主观臆断、初始值要求较高或不收敛等技术问题。针对此问题，已进行了一定修正，取得了一定效果，但是对于复杂计算，特别是含固态产物的计算，仍然存在很大困难，且计算初始值设置要求高的问题仍未得到解决，无法实现同一系列多种配方炸药爆轰参数的计算[9]。为此，构建新型爆轰产物计算方法并解决计算收敛问题，对于爆轰参数的准确计算具有重要意义。遗传算法是近年来基于基因遗传以及生化进化理论而提出的一种寻优方法，具有全局优化、操作简便以及较强的鲁棒性等特点，在单目标寻优、多目标寻优、参数优化、计划调度等方面得到了广泛应用[10-12]。目前，遗传算法已经开始应用于化学平衡计算，如范磊等[13]、安维中等[14]采用遗传算法对含化学反应体系的相平衡进行求解，取得了良好效果。基于此，本文中拟以CHON类炸药为典型，在现有爆轰参数计算总体框架[7]的基础上，引入遗传算法，建立炸药爆轰参数的计算方法，并验证计算结果的正确性，以期为炸药配方研制与性能预估奠定技术基础。

1 计算模型

炸药爆轰基本方程如下[15]，其中，式(2)为C-J条件，式(3)为气态爆轰产物状态方程(BKW)，式(4)为固态爆轰产物状态方程(Cowan状态方程)：

(1)

(2)

(3)

(4)

炸药爆轰参数理论计算即为式(1)～(4)的理论求解，主要包含在给定温度和压力的条件下爆轰产物组成的计算、在给定温度和压力的条件下炸药能量的计算、在给定压力的条件下温度的计算、C-J参数的求解等过程，具体可参考文献[9]，其中，爆轰产物组分含量的准确计算是爆轰参数理论计算的核心内容。下面主要结合遗传算法的特点阐述爆轰产物组分含量的计算原理和计算方法。

1.1 爆轰产物组分含量的计算原理

依据热力学平衡原理，爆轰组成即为炸药爆轰时爆轰产物体系自由能达到最小值时各组分的物质的量。为表述清楚，设气态产物各组分的物质的量为x1，x2，…,xN，固态产物各组分的物质的量为xN+1，xN+2，…,xM，则体系自由能F可表述为[7]：

(5)

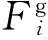
(6)

(7)

式中:Vs为固态产物压缩后的体积，cm3。

式(5)中气态爆轰产物和固态爆轰产物同时还需满足以下约束条件：

(8)

式中:aij为第i种爆轰产物组分分子式中第j种元素的个数；xi为爆轰产物i的物质的量；Nj为炸药中第j种元素的物质的量；l为炸药分子式中元素的总数。

爆轰产物组成计算即在满足式(8)的条件下，使得式(5)达到最小值时所求得的爆轰产物组分i的物质的量xi。

1.2 计算方法

炸药爆轰产物组成计算框图如图1所示。具体计算步骤如下：(1)输入初始条件，包含混合物分子式CaHbOcNd、生成焓ΔHf(kJ/kg)、压力p、温度T。(2)输入计算控制条件，包含种群大小NIND、最大迭代次数MAXGEN、变量数NVAR、变量字节数PRECI、代沟GGAP，其中，NIND取值为250，以保证充足的样本数；MAXGEN取值为2 000；NVAR依据炸药组分数目而定；PRECI取值为20，以保证计算精度达到10-6以上；GGAP设置默认值为0.7。(3)依据可能的爆轰产物组分，确定独立组分的数目(即NVAR)以及变化范围。(4)计算目标函数值并将其作为初始值，进入包含适应度、选择、交叉、变异的循环计算，当条件满足时跳出计算。(5)最后，输出爆轰产物组分含量。计算中，遗传算法中自变量的选取变化范围的确定、目标函数与适应度函数是遗传算法中的核心内容。

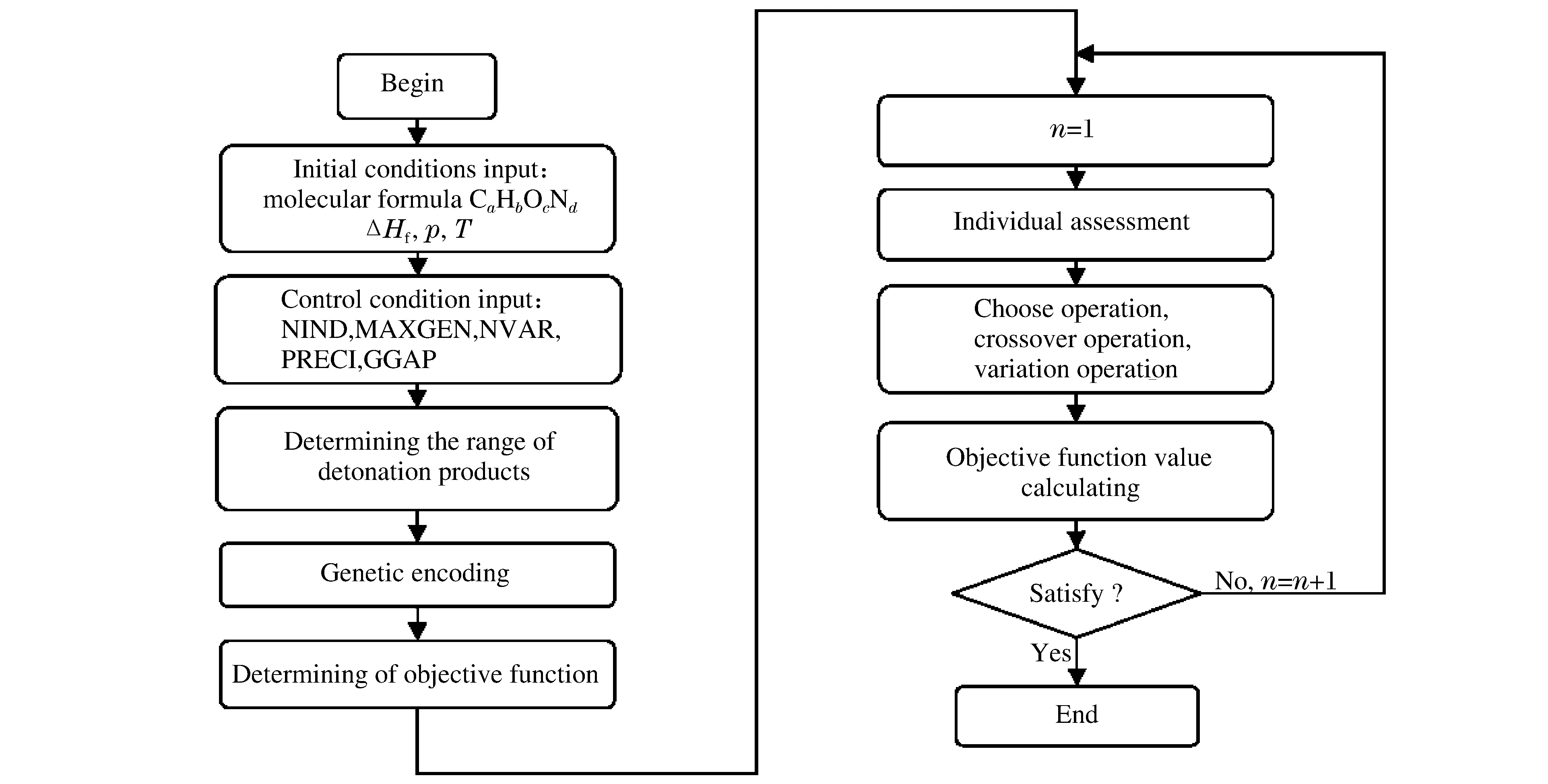
图1 爆轰产物组成计算流程图 Fig.1 Calculation process for the content of detonation products

1.2.1 独立组分的选取和变化范围的确定

[5,7,11]，CHON类化合物的分子式可表示为CaHbOcNd(下标表示1 kg化合物中相应元素的物质的量)，可能的爆轰产物组分(14种)的物质的量表示为：x(Cs)、x(CO2)、x(CO)、x(CH4)、x(H2O)、x(H2)、x(H)、x(OH)、x(NH3)、x(N2)、x(N)、x(NO)、x(NO2)、x(O)。由于各组分的物质的量满足式(8)，因此将式(8)展开为：

(9)

根据式(9)可将4种组分的物质的量表示为其他组分的物质的量的线性关系式，使得独立变量由14个减少至10个，进而最小自由能函数可表示为10个自变量的函数，同时，求解问题由线性化约束问题转化为线性化非约束问题。

独立组分的选取和变化范围的确定，原则上可以从爆轰产物中任取10种组分，只要涵盖所有元素即可，但是由于各组分的物质的量差异较大，任意选定的自变量不容易确定其变化范围。考虑到爆轰产物中一些组分的物质的量较少，变化范围容易确定，首先将其选作自变量，然后补充一定的主要成分。对于CHON类化合物，首先选取x(CH4)、x(H)、x(OH)、x(NH3)、x(N)、x(NO)、x(NO2)、x(O)作为自变量，再添加x(Cs)、x(CO2)共同组成10个自变量，然后通过文献[6]中火炸药燃烧产物组分含量的统计与整理，以较大上限确定各组分含量变化范围:

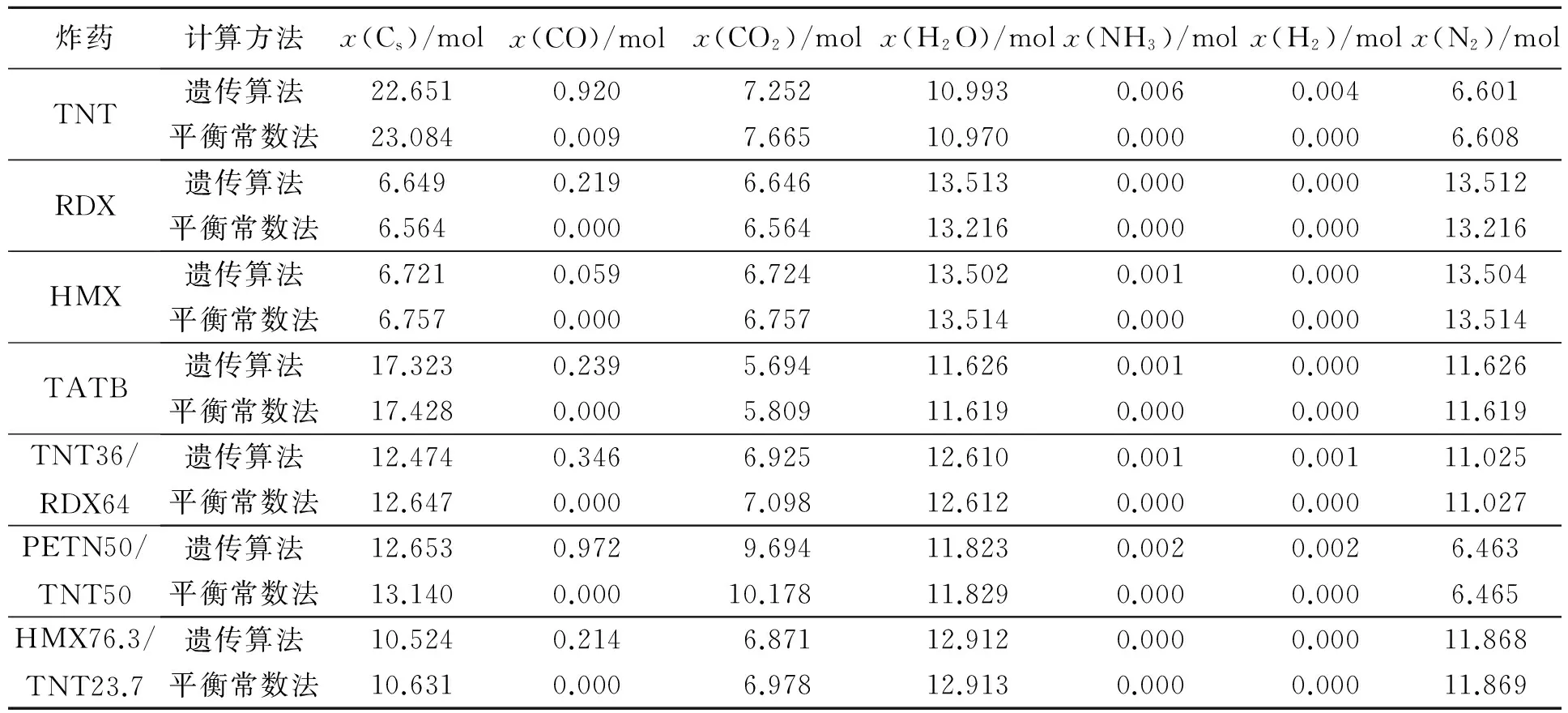
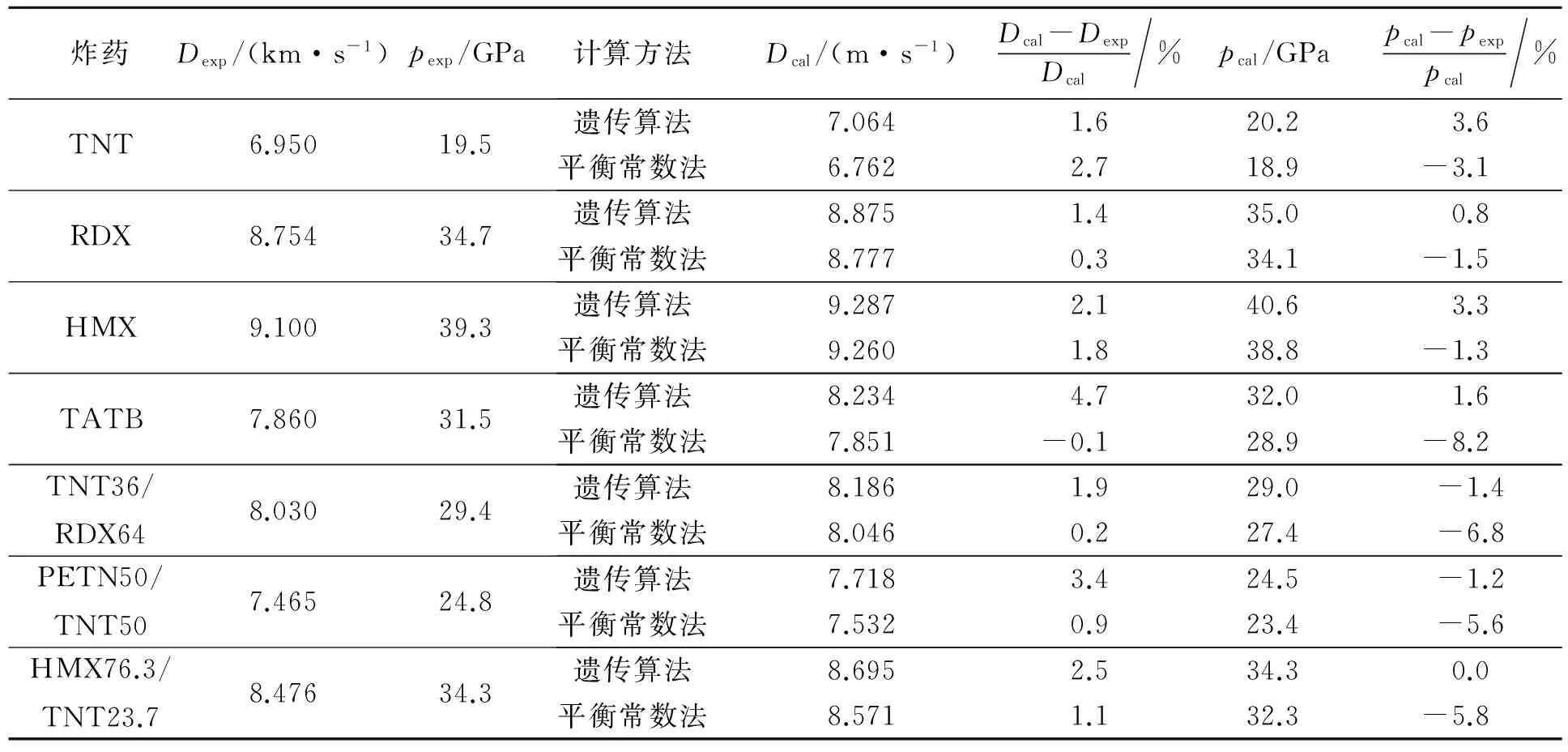
0

0

0

其中除x(Cs))和x(CO2)需要根据不同系列炸药稍作调整外，其他变量的取值范围无需变化就可满足爆炸产物计算需求。显然，相对于泰勒展开法等对各组分初始值设置应与真值相接近的严格要求，本方法计算简便且可适应于同一系列多种炸药配方的优化计算。

1.2.2 目标函数和适应度函数的确定

适应度G是与目标函数值接近程度相对应的评价个体优劣的参数，越接近于目标函数值，则个体对应的适应度值越大，个体越容易继承。根据爆轰产物计算的特点，本文中直接将目标函数(体系自由能F)作为判别个体优劣的适应度函数，并添加正数2 000以保证目标函数值为正。另外，由于各变量在其变化范围内是随机抽取的，很有可能出现组分物质的量为负值而不满足式(8)的情况，为使其在迭代过程中被淘汰，本文中设定其为10 000，以减少其适应度。适应度函数如下：

(10)

2 计算结果与分析

为验证本文计算方法的精度和可行性，选取TNT(C30.84H22.03O26.43N13.22)、RDX(C13.51H27.03O27.03N27.03)、HMX(C13.51H27.03O27.03N27.03)、TATB(C23.26H23.26O23.26N23.26)典型单质炸药和TNT36/RDX64(C19.75H25.23O26.81N22.05)、PETN50/TNT50(C23.33H23.67O32.20N12.94)、HMX76.3/TNT23.7(C17.62H25.84O26.89N23.74)典型混合炸药作为计算对象，对其爆轰参数进行计算，计算结果列于表1～2中，为便于比较，将以平衡常数法为基础的爆轰参数计算结果[6]以及实验结果[1]也一并列入表中。计算时所用的炸药质量均为1 kg,且TNT的初始密度为1.64 g/cm3,RDX的初始密度为1.80 g/cm3,HMX的初始密度为1.90 g/cm3,TATB的初始密度为1.895 g/cm3,TNT36/RDX64的初始密度为1.713 g/cm3,PETN50/TNT50的初始密度为1.65 g/cm3,HMX76.3/TNT23.7的初始密度为1.809 g/cm3。

表1 不同炸药爆轰产物各组分的物质的量的计算结果Table 1 Amount of substance calculted by different methods for different detonation products of different explosives

从表1中典型单质炸药和混合炸药爆轰产物组分含量的计算结果可以看出：采用遗传算法和平衡常数法计算所得主要组分物质的量非常接近，Cs、CO2、H2O、N2等主要组分物质的量的计算结果相差在6%以内，一定程度上验证了遗传算法在爆轰产物组分含量计算中的准确性，但是两者在微量组分的计算中仍存在较大差异，其中，平衡常数法计算结果趋近于零，典型的如CO、H2等。具体分析原因可知：平衡常数法在计算过程中由于采用水汽平衡方程来简化计算，计算过程存在一定的人为干预，加之水汽平衡方程中平衡常数是依据一定温度和压力条件下拟合得到的，其与实际情况存在一定的差异，最终导致微量组分含量趋近于零；而遗传算法在计算过程中仅涉及爆轰产物在不同温度下的自由能，不需要选取各组分间化学反应的平衡常数，且计算过程完全脱离了人为干预，因此其计算结果可信度更高。

表2中Dcal为爆速计算结果，Dexp为爆速实验结果，pcal为爆压计算结果，pexp为爆压实验结果。从表2可以看出，以平衡常数法为基础的爆速计算结果尽管与实验结果吻合较好，误差在5%以内，但其爆压计算结果误差较大，最大误差达8%以上。而相比之下，以遗传算法为基础的爆速和爆压的计算结果则与实验测试结果吻合更好，爆速和爆压计算结果误差都在5%以内。

分析原因可知，当采用BKW状态方程计算炸药爆轰参数时，由于爆轰产物各组分余容对总余容的影响较小，为此，尽管采用遗传算法与平衡常数法计算得到的爆轰产物组分的物质的量存在一定的差异，但其对炸药爆速的影响较弱，以致于两者爆速计算结果与实验结果吻合较好；另一方面，由爆压与爆速的关系：p=ρ0D2/(1+γ)可知，当炸药密度、爆速一定时，炸药爆压主要受多方指数的影响，而多方指数又是与炸药爆轰产物组分密切相关的，为此，精确的爆轰产物计算结果是影响炸药爆压变化的主要原因，对比两种方法计算得到的结果与实验结果的符合程度可以看出，本方法具有更高的精度和准确度。

表2 不同方法得到的不同炸药的爆轰速度和爆轰压力Table 2 Detonation velocity and pressure obtained by different methods for different explosives

3 结 论

(1)在最小自由能原理的基础上，引入遗传算法建立了炸药爆轰参数理论计算模型，形成了爆轰参数计算方法，为炸药配方设计与性能预估奠定了理论基础。

(2)本计算方法精度高、人工干预弱，单质炸药和混合炸药爆轰参数计算结果误差在5%以内，可望在混合炸药等爆轰参数计算以及多配方优化计算中得到应用。

参考文献：

[1] Mader C L. Numerical modeling of explosive and propellants[M]. 2nd ed. Florida: CRC Press, 1998:33-52.

[2] Qiu Jianbin, Feng Gang, Gao Huijun. A new equation of state for detonation products[J]. Journal of Chemical Physics, 1981,74(8):4634-4645.

[3] 李德华,程新路,杨向东,等.TNT 和TATB 炸药爆轰参数的数值模拟[J].兵工学报,2006,27(4):638-642. Li Dehua, Cheng Xinlu, Yang Xiangdong, et al. Numerical simulation of detonation parameters for TNT and TATB detonation products[J]. Acta Armamentarii, 2006,27(4):638-642.

[4] Wu Xiong. Detonation performance of condensed explosives computed with the VLW EOS[C]∥Proceedings of the Eighth Symposium (International) on Detonation. Albuquerque: Office of Naval Research, 1986:796-804.

[5] 吴雄,龙新平,何碧,等.VLW爆轰产物状态方程[J].中国科学:B辑:化学,2008,38(12):1129-1132.

[6] 周霖.爆炸化学基础[M].北京:国防工业出版,2005:33-37.

[7] 孙志艳,潘功配,陈宁,等.底排药剂燃烧产气量的理论计算[J].弹箭与制导学报,2006,26(2):71-73. Sun Zhiyan, Pan Gongpei, Chen Ning, et al. Calculation of gaseous products quantity for base bleeding agent[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006,26(2):71-73.

[8] 周霖,谢中元.含Cs盐推进剂燃烧产物导电特性研究[J].含能材料,2009,17(1):99-102. Zhou Lin, Xie Zhongyuan. Research on electrical conductivity of combustion production of composite propellant containing Cs salt[J]. Chinese Journal of Energetic Materials, 2009,17(1):99-102.

[9] 张熙和,云主惠.爆炸化学[M].北京:国防工业出版社,1989:23-35.

[10] 雷英杰,张善文,李续武,等.Matlab遗传算法工具箱及其应用[M].西安:西安电子科技大学出版社,2011:45-61.

[11] Goldberg D E. Genetic algorithms in search, optimization and machine learnin[M]. Boston: Addison-Wesley Professional, 1989:1-25.

[12] 谢中元,周霖,王浩,等.遗传算法在推进剂燃烧产物组成计算中的应用[J].含能材料,2015,23(4):340-345. Xie Zhongyuan, Zhou Lin, Wang Hao, et al. Application of genetic algorithm in calculation of combustion equilibrium composition[J]. Chinese Journal of Energetic Materials, 2015,23(4):340-345.

[13] 范磊,潘功配,欧阳的华,等.基于遗传算法结合支持向量机的Mg/PTFE贫氧推进剂配方优化[J].推进技术,2012,33(4):620-624. Fan Lei, Pan Gongpei, Ouyang Dehua, et al. Application of genetic algorithm-support vector machine in formula optimization of Mg/PTFE fuel rich propellant[J]. Journal of Propulsion Technology, 2012,33(4):620-624.

[14] 安维中,胡仰栋,袁希钢.多相多组分化学平衡和相平衡计算的遗传算法[J].化工学报,2003,54(5):691-694. An Weizhong, Hu Yangdong, Yuan Xigang. Calculation of multiphase and multicomponent chemical equilibrium using genetic algorithm[J]. Journal of Chemical Industry and Engineering, 2003,54(5):691-694.

[15] 陈朗,龙新平.含铝炸药爆轰[M].北京:国防工业出版社,2004:30-38.

[16] 宁小蘶.炸药水下爆炸性能计算方法研究[D].北京：北京理工大学,2010:10-21.

(责任编辑 张凌云)

Application of genetic algorithm to calculation of detonation parameters

Xie Zhongyuan1, Wang Xiaofeng1, Wang Hao1, Zhou Lin2

(1.Xi’anModernChemistryResearchInstitute,Xi’an710065,Shaanxi,China; 2.StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China)

To solve the problems of bad convergence and to satisfy the strict requirement to initial conditions in the calculation of detonation parameters, a new calculation method was proposed based on the principles of chemical equilibrium and the method of minimum free energy by introducing the genetic algorithm, and the calculated results of typical explosives were compared with the experimental data to verify the validity and the accuracy of the new method. It is demonstrated that, by the new method, the calculated results of detonation pressure and velocity of the explosives correspond well with the experimental data with the errors under 5%, which can be applied to predict explosive properties. Also, the computational process is convenient with little manual intervention and entails only the verification of the moles variation form of the few major ingredients, which may be used for multi-formula optimization design.

mechanics of explosion; genetic algorithm; minimum free energy; detonation parameters

10.11883/1001-1455(2016)04-0503-06

2014-12-24；

2015-04-21

国家自然科学基金项目(11502194)

谢中元(1982— )，男，博士，副研究员,408671355@qq.com。

O381; TJ012.1国标学科代码：13035

A