传动齿隙对电视导引头伺服系统稳定性的影响分析*

游培寒,缪 昕,祝逢春,孙 靖,赵未平

(1 95856部队,南京 210000;2 解放军理工大学,南京 210007)

传动齿隙对电视导引头伺服系统稳定性的影响分析*

游培寒1,缪 昕2,祝逢春1,孙 靖1,赵未平1

(1 95856部队,南京 210000;2 解放军理工大学,南京 210007)

电视导引头伺服系统传动齿隙是产生图像抖动的重要因素,为了分析齿隙大小与图像抖动幅度的关系,文中在某型电视导引头伺服系统模型基础上,采用描述函数法建立传动齿隙的非线性模型,根据推广的奈奎斯特稳定性判据分析缝隙大小对系统稳定性的影响,并用图解法推导计算系统自振频率和幅度,最后推导出齿隙大小与电视导引头图像抖动幅度关系,并通过Simulink建模仿真验证了计算方法有效性。

传动齿隙;伺服系统;Simulink仿真

0 概述

由于控制精度要求较高,大多数电视导引头都采用齿轮传动平台式伺服系统,影响其性能的非线性因素包括系统死区、摩擦、饱和、齿隙等;其中齿隙是影响伺服控制系统控制精度的主要因素[1-3],装配、磨损等因素造成齿隙实际难以避免,齿隙的存在造成系统自振,影响电视导引头成像清晰度,严重时系统将难以锁定目标或图像目标丢失。某型制导炸弹导引头伺服系统采用三自由度平台式结构,其中内框与中框用于俯仰和偏航方向角度调整,两框均采用直流电机驱动,单级齿轮传动,各框主动轮固联于直流电机力矩输出轴,从动轮固联于活动框架,各框上安装有角速率陀螺,并通过底部速度控制器形成平台速度环控制回路;安装在内框上的电视跟踪器可以实时检测目标与视场中心的角度差并传输给速度控制器,从而构成位置环控制回路;为了节省篇幅,文中以下以内框为例进行分析,其结构如图1所示。

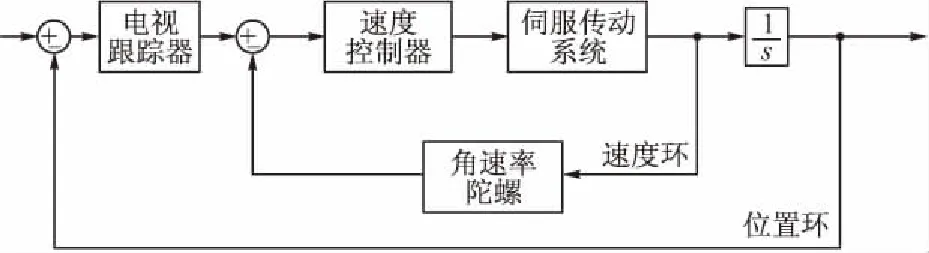
图1 电视导引头伺服控制系统结构图

文中构建内框控制回路模型,并对相关模块进行合理简化,第二部分将介绍考虑齿隙的伺服传动模型;第三部分将介绍控制回路模型;第四部分推导系统奈奎斯特稳定性判据公式;第五部分计算自振频率和幅度等参数。第六部分给出齿隙与图像抖动幅度的关系。

1 考虑齿隙的伺服传动模型

伺服传动系统模型如图2所示,可以用如下微分方程组表示[1]:

(1)

图2 伺服传动系统模型

其中:Ke是直流电机的电势反馈增益;θ1、θ2分别是主动、从动轮转动角度;Re是电机电枢电阻;Le是电枢电感;J1、J2分别是主动、从动轮转动惯量;b1、b2分别是主动、从动轮摩擦系数;Km为电机力矩系数;i为传动比;Ue是功率放大模块的输出电压;Ie为电机电枢电流。考虑系统存在齿隙,式(1)中θ1需要用非线性函数φ(θ1)替代,则(式1)变为:

(2)

式(2)拉氏变换为:

(3)

式中:s为拉氏变换符号;L[φ(θ1)]为φ(θ1)的拉氏变换,其解析解相对复杂,无法进行稳定性分析。采用描述函数法[2]对其建模,其原理是假设齿隙前主动轮转角θ1=Asinωt,ω为齿隙输入正弦波角速度,A为正弦波幅度,则齿隙系统输出波形为:

(4)

式中:a为齿隙宽度;α为齿隙宽度对应相位角宽。式(4)频率变换后的0阶项为零,由于伺服控制系统的低通滤波特性,高阶项失效,只取其一阶项组成L[φ(θ1)]的描述函数:

(5)

这里j表示虚部符号。在稳定性分析中,可将L[φ(θ1)]=N(A)θ1代入式(3),得到齿轮传动模型Ge(s):

(LeJ1b2i+LeJ2b1i+J1J2Rei)s3+(KmKeJ2i+

ReJ1b2i+ReJ2b1i+k12LeJ1+Leb1b2i+

LeJ2k12N(A)i)s2+(KeKmb2i+ReJ1k12+Reb1b2i+

ReJ2k12N(A)i+Leb1k12+Leb2k12N(A)i)s+

(KeKmk12+Reb1k12+N(A)k12Reb2i)]

(6)

2 控制系统模型

除了齿轮传动模型外,控制系统还包括速度控制器、角速率陀螺、电视跟踪器等子系统。速度控制器一般采用PID控制[4],其主要作用是提高系统抗干扰能力和优化速度环带宽,可以用下式表示[3]:

(7)

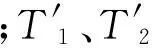
Gg(s)=Kg

(8)

则速度环传递函数Gw(s)为:

[T1T2s2+(T1+T2)s+1]KcKmk12N(A)i/

{[J1J2Leis4+(LeJ1b2i+LeJ2b1i+J1J2Rei)s3+

(KmKeJ2i+ReJ1b2i+ReJ2b1i+k12LeJ1+Leb1b2i+

LeJ2k12N(A)i)s2+(KeKmb2i+ReJ1k12+Reb1b2i+

ReJ2k12N(A)i+Leb1k12+Leb2k12N(A)i)s+

(T1+T2)s+1]KcKmk12N(A)i}

(9)

电视跟踪器是位置环中的主要器件,其传递函数可以用一个延迟网络表示:GT(s)=e-τs≈1-τs,则位置环开环传递函数GK(s)为

{KcKmk12N(A)i[-T1T2τs3+

(T1T2-T1τ-T2τ)s2+(T1+T2-τ)s+1]}/

(KmKeJ2i+ReJ1b2i+ReJ2b1i+k12LeJ1+Leb1b2i+

J1J2Rei)+(KeKmb2i+ReJ1k12+Reb1b2i+

(KmKeJ2i+ReJ1b2i+ReJ2b1i+k12LeJ1+Leb1b2i+

ReJ1k12+Reb1b2i+ReJ2k12N(A)i+Leb1k12+

ReJ2b1i+k12LeJ1+Leb1b2i+LeJ2k12N(A)i)+

KgKcKmk12N(A)iT1T2)s3+((KeKmk12+Reb1k12+

Reb1b2i+ReJ2k12N(A)i+Leb1k12+Leb2k12N(A)i)+

KgKcKmk12N(A)i(T1+T2))s2+(KeKmk12+

Reb1k12+N(A)k12Reb2i+KgKcKmk12N(A)i)s}

(10)

3 伺服系统奈奎斯特稳定性判据

系统临界稳定时有如下关系1+GK(s)=0,则有式(11)。根据推广的奈奎斯特稳定性判据,当GN(s)的奈奎斯特曲线不包围负-1/N(A)时系统稳定,否则系统不稳定或者自振。

LeJ2k12i+KgKcKmk12iT1T2-KcKmk12iT1T2τ)s3+

KgKcKmk12i(T1+T2)+KcKmk12i(T1T2-T1τ-

T2τ))s2+(k12Reb2i+KgKcKmk12i+KcKmk12i(T1+

LeJ2b1i+J1J2Rei)+(KeKmb2i+ReJ1k12+Reb1b2i+

ReJ2b1i+k12LeJ1+Leb1b2i))s3+((KeKmk12+

Reb1b2i+Leb1k12))s2+(KeKmk12+Reb1k12)s]

(11)

4 自振频率和自振幅度

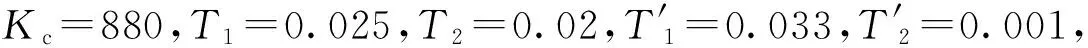
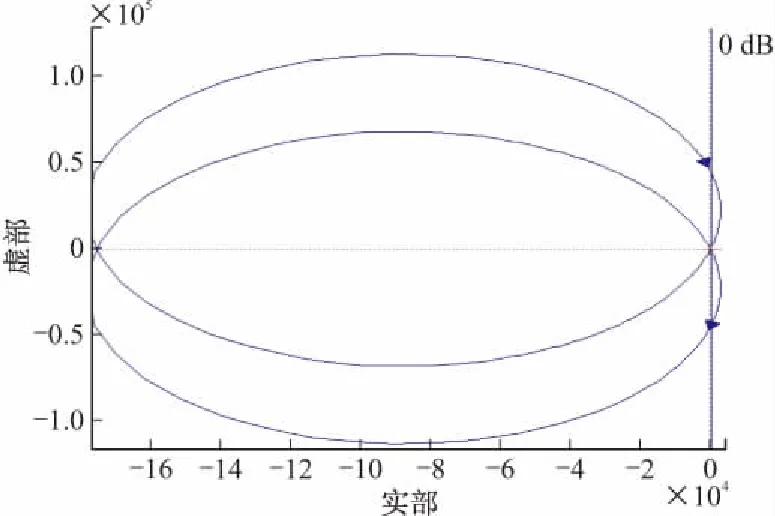
图3 伺服系统奈奎斯特曲线

通过式(5)可以发现-1/N(A)曲线只和A/a有关,与齿隙宽度a无关,当A>a时,绘制-1/N(A)曲线如图4所示,则-1/N(A)与GN(s)交点为:

(12)

GN(ωj)奈奎斯特曲线与-1/N(A)的交点就是系统自振点,则自振时Nz(A)=0.497 1-0.318 6j,代入式(5)解得:

(13)

可见自振幅度会随着齿隙宽度增大而增大,通过观察GN(ωj)奈奎斯特曲线,可以发现交点处系统自振频率约为ωz≈86.8 rad/s。

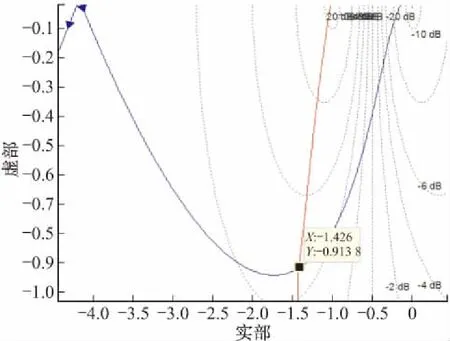
图4 伺服系统稳定性临界点

利用Simulink搭建电视导引头控制系统仿真模型如图5所示,系统在齿隙处的自振幅值和自振频率与文中计算结果较为一致,图6为齿隙宽度a=0.001 rad时的齿隙前后自振波形。

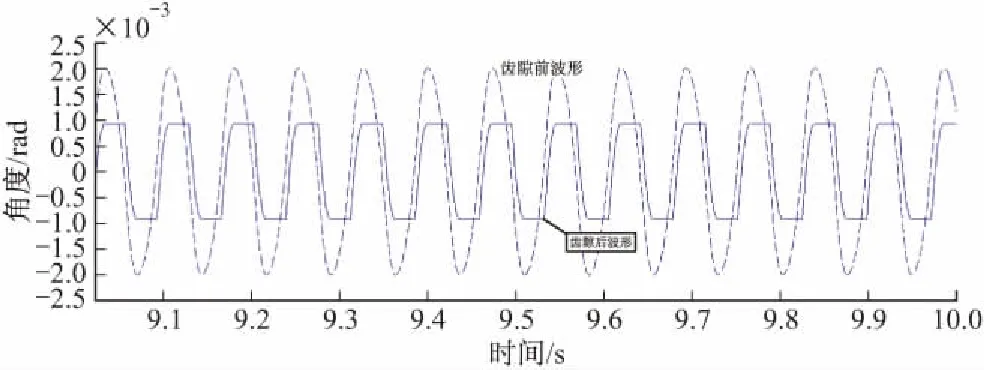
图6 齿隙前后的自振波形

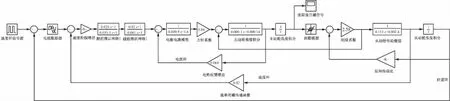
图5 考虑齿隙的电视导引头控制系统仿真模型

5 齿隙与成像抖动幅度

通过式(2)和式(13)可以推导出镜头抖动(位置环振幅)A1与齿隙前振幅的关系:

(14)

将上文参数代入,通过式(14)可以计算镜头抖动幅度A1,如当a=0.001 rad时,A1=3.6×10-6rad。通过Simulink仿真得到在齿隙宽度分别为a=0.001 rad、0.01 rad和0.02 rad时的伺服系统位置环输出速度信号如图7所示,与式(14)计算结果一致。可以看出随着齿隙的增大,位置环输出镜头抖动幅度会越来越大,从而影响电视成像精度。

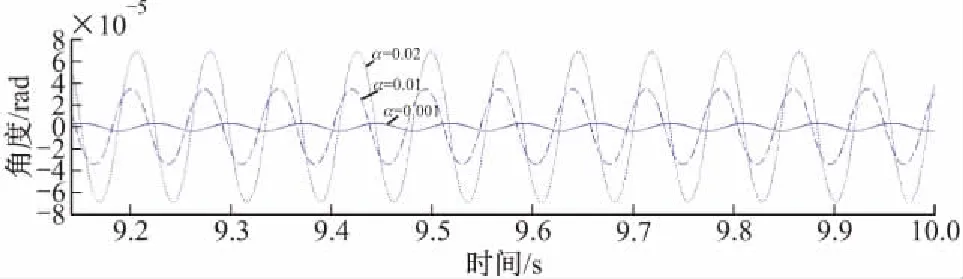
图7 镜头抖动幅度随齿隙宽度变化

6 结论

文中利用描述函数法分析了齿隙与电视导引头伺服系统自振的关系,计算了自振频率和幅度等参数,并分析了齿隙对导引头镜头抖动幅度的关系。通过Simulink搭建电视导引头控制系统模型,仿真验证了计算方法的有效性。

[1] 王建侠. 多电机同步联动系统的动力学建模及消隙控制算法研究 [D]. 南京: 南京理工大学, 2004.

[2] 袁新星. 多电机同步联动消隙伺服系统动力学建模与控制研究 [D]. 南京: 南京理工大学, 2014.

[3] 苗少帅. 导引头伺服机构谐振频率与去偶精度分析 [D]. 长沙: 国防科技大学, 2008.

[4] 王秋平, 左玲. 光电跟踪伺服系统的位置超前抑制法 [J]. 弹箭与制导学报, 2012, 31(1): 7-8.

[5] 欧朝华. 电视末制导导引头伺服系统的研制 [D]. 哈尔滨: 哈尔滨工业大学, 2007.

Analysis of the Impact of Transmission Backlash on the Stability of TV-seeker Servo System

YOU Peihan1,MIAO Xin2,ZHU Fengchun1,SUN Jing1,ZHAO Weiping1

(1 No.95856 Unit, Nanjing 210000, China; 2 PLA University of Science and Technology, Nanjing 210007, China)

Transmission backlash of TV-seeker servo system was an import influence factor for image vibration. In order to analyze the relationship between transmission backlash width and image vibration amplitde, this paper used describing function method to construct non-linear model of transmission backlash.According to Nyquist stability criterion, the effect of gapsize on the stability of the system was analyzed. And the natural frequency and amplitude of the system were deduced by graphic method. Finally we got the relationship between the TV-seeker’s image vibration magnitude and the backlash size. Using Simulink we constructed a whole servo system model to test the effectiveness of the new analysis method.

transmission backlash; servo system; Simulink simulation

2016-01-06

游培寒(1978-),男,江苏南京人,工程师,博士,研究方向:航空弹药与制导控制。

TJ765

A