钢梁与混凝土墙铰接节点嵌固弯矩的计算方法

Calculation Methods for Partially Restrained Moment at Bolted Connection Joint of Steel Beam to Concrete Wall

周承宗（同济大学建筑工程系，上海　200092）



钢梁与混凝土墙铰接节点嵌固弯矩的计算方法

Calculation Methods for Partially Restrained Moment at Bolted Connection Joint of Steel Beam to Concrete Wall

周承宗
（同济大学建筑工程系，上海200092）

摘要：钢梁与混凝土墙铰接节点是外钢框架-混凝土核心筒结构中常见的一种节点连接形式，在其预埋件的设计计算中，需要考虑节点连接处嵌固弯矩的影响。该文讨论了钢梁与混凝土墙的铰接节点嵌固弯矩的形成原因及受力特点，介绍了嵌固弯矩的理论计算方法、Crawford计算方法及规范建议方法，并对三类方法进行了对比。研究表明，采用规范建议的方法可得到偏于安全的结果。

关键词：钢梁-混凝土墙节点；嵌固弯矩；螺栓连接；方法对比

Abstract:The pinned connection joint of steel beam to concrete wall is a common practice in steel frame and concrete core tube structure. In the design for the embedded part of the connection，the partially restrained moment must be taken into account. In this paper，the causes and features of partially restrained moment are discussed; and the calculation methods like theoretical method，Crawford method and code recommended method are also introduced and compared among each other. The study shows that the code recommended method can obtain a reasonable result.

Keywords:connection of steel beam to concrete wall; partially restrained moment; bolted connection; methods comparison

0　引言

近年来，外钢框架-混凝土核心筒结构在我国高层建筑中的应用逐渐增多，钢梁与混凝土墙铰接节点已成为这种混合结构中一种常见的节点连接形式。例如在上海世博“绿谷”A片区B2塔楼的三层钢结构夹层中，为了避免结构三层处形成薄弱层，该层的钢梁与混凝土墙柱连接节点被设计成铰接，如图1所示。这种铰接节点是将钢梁腹板与混凝土墙中预埋件上的连接钢板通过螺栓连接，预埋件则通常利用栓钉埋置于混凝土墙中。事实上，由于混凝土墙不宜承受较大的出平面集中弯矩，当混凝土墙内无钢骨时，钢梁与墙的刚接连接构造是不稳定的，因此常被建议做成铰接，并且在结构内力分析时按铰接考虑。

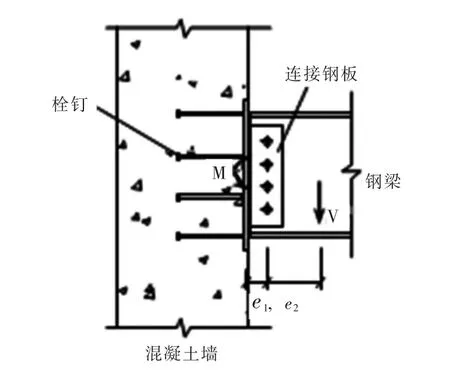
图1　钢梁与混凝土墙的连接

钢梁与混凝土铰接节点设计的关键问题在于计算钢梁传给预埋件的剪力和弯矩，进而验算预埋件及栓钉的承载力。预埋件承受的剪力等于钢梁梁端的剪力V，而所承受弯矩的计算却有待探究。一方面，如果简单地按照铰接节点设计计算，埋件所承受的弯矩为偏心弯矩；另一方面，由于节点螺栓群的嵌固作用，钢梁无法充分自由转动，实际节点并非完全的铰接节点，而更应该被视作为半刚性节点，所以预埋件实际所承受的弯矩还应包括由于螺栓群嵌固作用形成的嵌固弯矩M2[1]，即预埋件所承受的总弯矩为M=M1+M2。嵌固弯矩的大小与螺栓群连接的刚度有关，由于螺栓连接的弹塑性性质，嵌固弯矩的计算比较复杂。本文分别介绍了嵌固弯矩的理论计算方法、Crawford计算方法及规范建议方法，并对三类方法进行了对比。

1　高强度螺栓的受剪工作性能

根据“强连接”设计准则，嵌固弯矩的大小应根据连接节点达到承载力极限状态时螺栓群受力的弹塑性状态来确定。可见，高强度螺栓的受剪工作性能是计算嵌固弯矩的基本问题。

参考文献[2]所建议的剪力-变形关系曲线如图2所示，分为四个阶段：摩擦传力的弹性阶段OA、滑移阶段AB、板孔壁挤压阶段BC和破坏阶段CD。摩擦型高强度螺栓是依靠连接板间的摩擦阻力来传递剪力的，以滑动时摩擦阻力Rs作为摩擦型连接的极限抗剪承载力。过B点后，滑移阶段结束，螺杆杆身与孔壁接触，使螺杆受剪和孔壁受压，螺栓连接由摩擦型转为承压型，受剪承载力可以继续增加，直至达到螺栓连接的极限承载力Ru，该值即为高强度螺栓的承压型连接的极限承载力。

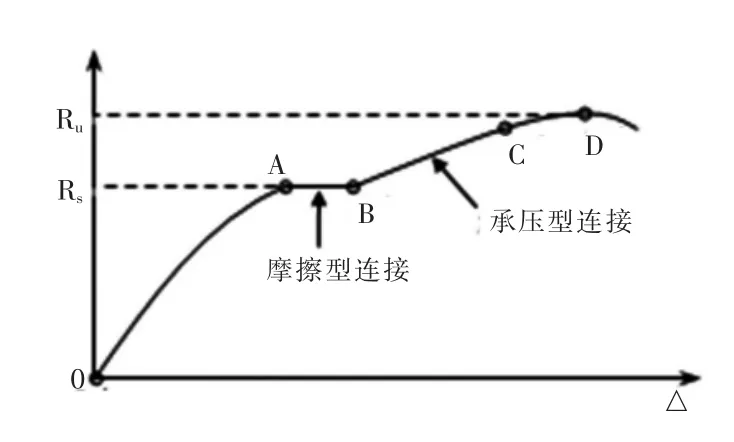
图2　高强度螺栓的受剪工作性能

2　嵌固弯矩计算的理论方法

螺栓连接的嵌固弯矩的计算简图如图3所示，在距离螺栓群竖向中心轴的e2处作用竖向剪力V，假定预埋件的连接钢板保持刚性，此时螺栓群绕某一瞬时中心O转动。当距离瞬时转动中心最远的螺栓达到其极限承载能力时，整个螺栓群连接也达到极限承载能力。此时螺栓群承受的弯矩即为嵌固弯矩，即M2=Ve2，称e2为折算偏心距。

对于承压型螺栓连接，按以下步骤计算螺栓群连接的嵌固弯矩及折算偏心距：

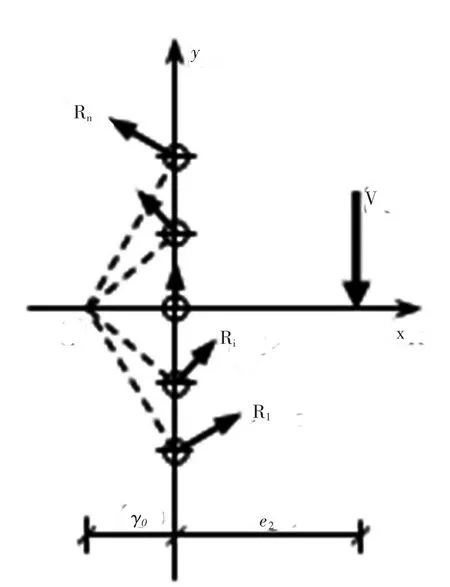
图3　嵌固弯矩的理论计算简图

（1）假定瞬时转动中心O的位置，该点定在通过螺栓群的中心与荷载P作用力方向垂直的直线上，瞬时转动中心到螺栓群形心之间的距离记为r0。

（2）距瞬时转动中心最远处rmax的螺栓达到极限剪切变形△u，螺栓所受剪力也达到其极限承载力Ru。各螺栓的剪切变形与该螺栓到瞬时转动中心的距离ri成正比，假定各螺栓所受的剪力Ri亦与ri成正比，同时按式（1）计算Ri的竖向分力Ri，v：

（3）计算所有螺栓剪力竖向分力合力，并与竖向剪力V进行比较，验算是否满足式（2）的平衡条件，若小于容许误差，则可解得r0。

若式（2）平衡条件不满足，则需重新选择一个新的r0，重复上述步骤，迭代求解r0直到能够满足式（2）的平衡条件为止。此时，螺栓群所承受的弯矩为各螺栓剪力对瞬时转动中心的弯矩之和，则嵌固弯矩及折算偏心距为：

对于摩擦型高强度螺栓连接，达到最大摩擦力时为极限状态，并认为所有的螺栓都达到滑动受剪承载力Rs。那么，极限状态时的竖向受力平衡条件简化为：

r0的迭代求解思路与承压型相同，然后将r0再代入式（3）即可得出摩擦型连接的嵌固弯矩及折算偏心距。可见，嵌固弯矩的大小与螺栓的数目及布置、梁端剪力大小均有关。

3　Crawford方法

Crawford等根据前述理论方法进行了大量的分析，提出了一个计算嵌固弯矩的简化方法[3]。基于此简化方法，Hawkins等针对图1所示的钢梁-混凝土墙连接节点，提出了预埋件所承受的最大弯矩的近似经验计算方法[4]。

式中，Asb为螺栓连接的受剪面积；Isb0为螺栓群对其形心的极惯性矩，即，其中，xi、yi为第i个螺栓的坐标；k为与螺栓群极惯性矩和折算偏心矩e2有关的系数，其中的参数α和β按下列公式确定：

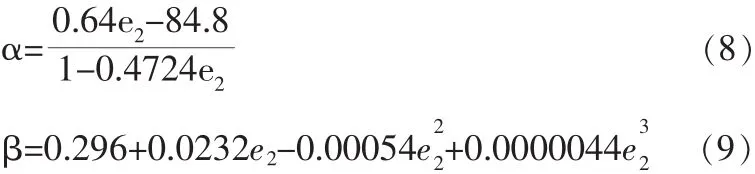
上述方法在计算时需k、α和β三个公式联立求解超越方程才能得到e2，较为复杂，使用十分困难。已经废止的中华人民共和国黑色冶金行业标准《钢骨混凝土结构技术规程》YB 9082-1997基于Crawford等的研究成果，在条文说明中列出了k-Isb0-e2的列线图，由其中第一式计算k值，由k值和Isb0值可查该图得偏心距e2，进而计算嵌固弯矩M2=Ve2。

4　规范建议的方法

替换YB 9082-1997的《钢骨混凝土结构技术规程》[5]YB 9082-2006及中国工程建设协会标准《高层建筑钢-混凝土混合结构设计规程》[6]CECS 230:2008给出了相对简单的近似弹塑性方法。考虑到螺栓群嵌固弯矩的弹塑性受力特点，其计算假定为：

（1）梁端剪力V在各个螺栓产生的竖向剪力均匀分配，水平剪力沿每列螺栓线性分布（如图4）。

（2）当离螺栓群形心最远的螺栓达到其极限受剪承载力Rm时，整个螺栓群也达到极限承载力。对于承压型螺栓，Rm取Ru；对于摩擦型螺栓，Rm取Rs。

对于图4所示的单列螺栓情况，由以上假定（1）可得极限状态时单个螺栓的竖向剪力和水平剪力分别为：

对螺栓群形心取矩，可得极限荷载V作用下的弯矩平衡方程为：

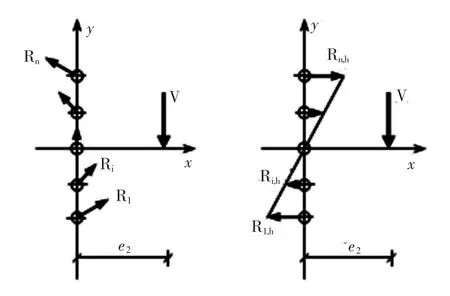
图4　规范建议方法的计算简图

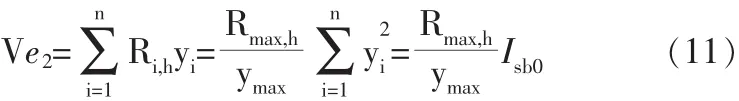
距螺栓群最远处螺栓的极限水平受剪承载力Rmax,h为：

代入式（11）即得：

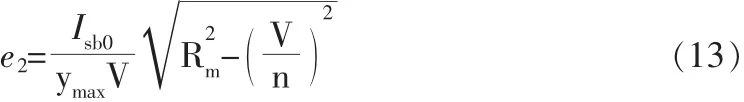
在计算嵌固弯矩时，需考虑预埋件的弯矩增大系数ηm，即M2=ηmVe2。其中，ηm在抗震等级为特一级时取1.5，一级取1.3，二级取1.2，三级取1.1，其他取1.0。

5　各类方法对比

对于承压型螺栓，假设采用10.9级M22螺栓，连接钢板厚t= 15mm，经计算得单个螺栓的极限承载力为Ru=188.1kN，螺栓行间距为70mm，一级抗震。分别利用上述理论方法、Crawford方法、规范建议方法，计算不同行数螺栓的嵌固弯矩，所得结果如表1所示。

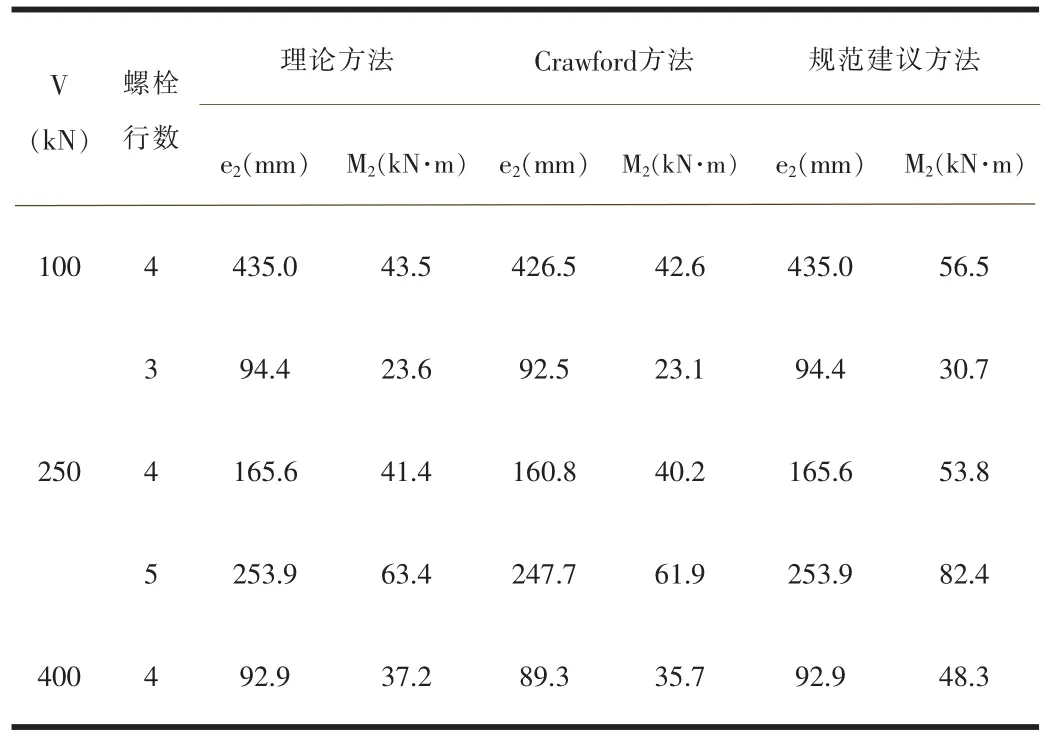
表1　承压型螺栓嵌固弯矩各计算方法对比

对于摩擦型螺栓，假设螺栓规格及布置与前述承压型相同，但单个螺栓的极限承载力为Rs=119.7kN，所得结果如表2所示。

对比以上计算结果，可得出以下结论：

（1）Crawford方法没有区分螺栓连接类型，所以表1及表2中的计算结果相同。采用Crawford方法得出的承压型螺栓连接的嵌固弯矩与理论方法接近，且比理论方法小，但在计算摩擦型螺栓连接时则与理论方法相差很大。可见，Crawford方法仅适用于高强度螺栓的承压型连接。

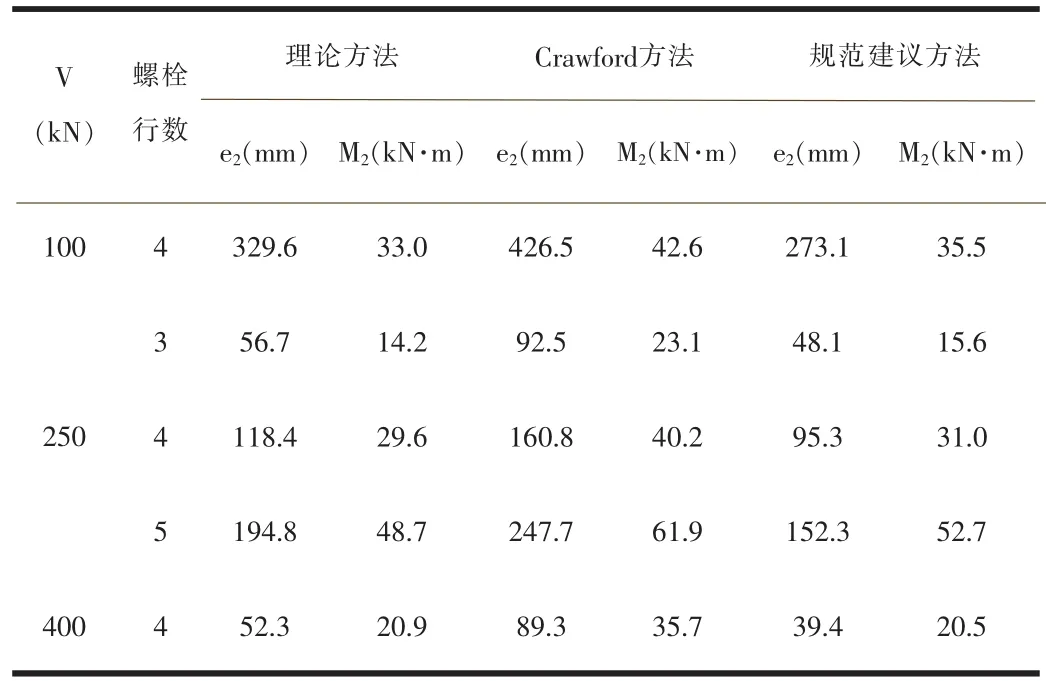
表2　摩擦型螺栓嵌固弯矩各计算方法对比

（2）采用规范建议方法，并考虑预埋件的弯矩增大系数ηm所计算得出的摩擦型螺栓连接的嵌固弯矩与理论方法接近，在计算承压型螺栓连接时则比理论方法大，在设计时采用该方法是偏于安全的。

6　结语

在计算钢梁与混凝土墙的铰接节点嵌固弯矩的各类方法中，理论方法需借助计算机编程实现迭代求解，求解过程复杂；而Crawford方法通过查图表求解，过程复杂，且所得结果较理论值小；采用规范YB 9082-2006及CECS 230:2008推荐的计算方法，过程简单，在设计时采用该方法可得到近似或偏于安全的计算结果。

[1]叶列平，郑从立，蔡益燕，等.钢梁-混凝土墙铰结连接节点嵌固弯矩的分析与计算[J].建筑结构学报，2006，27（5）: 30-38.

[2]沈祖炎，陈扬骥，陈以一.钢结构基本原理[M].北京：中国建筑工业出版社，2005.

[3] Crawford S F，Kulak G L.Eccentrically loaded bolted connections[J].Journal of the Structural Division，1971，97（3）: 765-783.

[4] Hawkins N M，Mitchell D，Roeder C W.Moment resisting connections for mixed construction [J].Engineering Journal，1980，17（1）.

[5]中冶集团建筑研究总院.YB 9082-2006钢骨混凝土结构技术规程[S].北京：冶金工业出版社，2007.

[6]中国建筑标准设计研究院.CECS 230:2008高层建筑钢-混凝土结构设计规程[S].北京：中国计划出版社，2008.

责任编辑：孙苏，李红

作者简介：周承宗（1991-），男，安徽六安人，硕士研究生，主要研究方向为工程结构的计算机数值仿真。

收稿日期：2016-01-11

doi：10.3969／j.issn.1671-9107.2016.03.060

中图分类号：TU312+.1

文献标识码：A

文章编号：1671-9107（2016）03-0060-03