基于联系数的区间二元语义模糊多属性群决策方法*

吴　群， 吴　澎， 周礼刚,2**

(1.安徽大学 数学科学学院，合肥 230601；2.南加利福尼亚大学 电气工程系信号与图像处理实验室，美国洛杉矶 加利福尼亚州 90089)



基于联系数的区间二元语义模糊多属性群决策方法*

吴群1， 吴澎1， 周礼刚1,2**

(1.安徽大学 数学科学学院，合肥 230601；2.南加利福尼亚大学 电气工程系信号与图像处理实验室，美国洛杉矶 加利福尼亚州 90089)

摘要：针对区间二元语义评价信息的不确定性，考虑区间二元语义变量取值的分布情况，定义了二元语义联系变量、二元语义正态分布变量，研究了它们的运算法则，并提出了二元语义联系变量信息集结算子；针对决策矩阵元素为区间二元语义变量属性权重完全未知的模糊多属性群决策问题，利用二元语义正态分布变量的方差，通过构建优化模型确定最优属性权重，提出了基于二元语义联系变量信息集成算子的模糊多属性决策方法，最后通过实例分析了方法的可行性和有效性.

关键词：多属性群决策；区间二元语义变量；二元语义联系变量；二元语义正态分布变量；信息集成算子

近年来，多属性群决策方法的研究已经取得了很大的进展.当属性值与属性权重都是确定的实数或语言评价信息时，已有很多成熟的解决方法，而在实际决策过程中，由于客观事物的复杂性、不确定性，以及人类思维的模糊性和决策者的主观性，决策者往往不能明确给出属性信息，而是以区间自然语言形式给出[1]，当属性权重或属性值含有一定的不确定性时，方案的排序一般也有一定的不确定性，这时就需要通过不确定性分析才能得到可靠的排序结果，因此对于这类区间多属性群决策问题的研究有着重要的理论意义和实际应用背景.自从西班牙学者Herrera 等[2]首次提出二元语义来描述语言评价信息，其对自然语言评价具有开创性的意义.近年来，对于区间二元语义评价信息的研究也引起了国内外众多学者的关注，其研究主要集中于两个方面：(1) 基于区间二元语义的信息集成算子研究.例如，文献[3]提出了基于语言值区间二元语义组能量平均(LI2TPA)算子，文献[4]提出了区间二元语义加权算术平均(IT-WAA)算子、区间二元语义有序加权平均(IT-OWA)算子、区间二元语义组合加权算术平均(IT-CWAA)算子等，这些集成算子在多属性群决策中得到了广泛应用；(2) 相关属性权重信息完全未知的情况下，建立一些优化模型，构建二元语义信息多属性决策方法.例如，文献[5]提出了一种基于区间二元语义信息处理和离差最大化的目标规划模型，文献[6]研究了基于极大熵和正理想方案的权重确定模型等.

但是这些基于区间二元语义的多属性群决策方法在处理区间二元语义多属性群决策问题时，均将二元语义评价信息落在区间二元语义评价信息中的分布看成服从均匀分布的，然而，区间二元语义信息反映的是对某个属性评价信息的变化范围，在此范围内的每一个评价信息均反映了决策者的决策态度，因此决策的方案优劣的排序与决策者的决策态度存在重要关系，需要通过决策者的风险态度分析才能做出更合理的决策；而另一方面，在实际过程中，考虑人类思维的惯性，属性评价信息落在区间二元语义评价信息中点的可能性最大，而越靠近区间二元语义评价信息端点时，落在其附近的可能性会逐渐减小，因此，可以将区间二元语义评价信息看成服从正态分布的.

从均匀分布和正态分布角度，考虑区间二元语义变量的分布情况.通过引入二元语义联系变量、二元语义正态分布变量，将区间二元语义变量表示为反映决策者的风险态度因子的二元语义变量形式，并提出了一些新的信息集成算子.解决问题的基本思路是：将区间二元语义变量转换成二元语义正态分布变量，根据二元语义正态分布变量方差和属性权重的随机性建立优化模型来确定最优属性权重，并将这些新的算子应用于模糊多属性群决策问题中，最后对综合评价二元语义联系变量中反映决策者的风险态度的不确定数i进行讨论，在不同情况下分析得到方案不同的排序结果，综合得到最终的排序结果，提高了区间二元语义模糊多属性群决策结果的可靠性与有效性.

1预备知识

定义1[7]若sk∈S是一个语言短语,则相应的二元语义形式可以通过函数θ获得,即

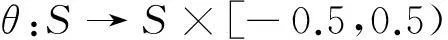
其中S是含有g+1个语言短语的语言评价集.

定义2[7]设实数β∈[0,g]为语言评价集S经过集结方法得到的实数,g+1为语言评价集S中元素的个数, 则β可以由函数Δ表示二元语义信息, 即

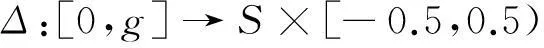
其中round为四舍五入取整算子.

定义3[7]若(sk,α)为二元语义信息, 其中sk为S中第k个元素,α∈[-0.5,0.5). 则存在一个逆函数Δ-1, 使其转换成相应的数值β, 即

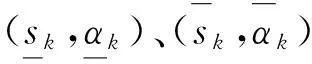
集对分析(Set Pair Analysis，简记为SPA)理论是我国学者赵克勤于1989年首次提出并用以研究不确定性的数学方法，从理论上承认了客观事物的模糊不确定性的存在，集对分析理论的提出，刻画了研究对象模糊不确定性以及模糊不确定性和确定性之间的相互联系、相互影响的关系.

联系数[9]是集对分析中给出的一个数学工具，其一般形式为

u=A+Bi+Cj

(1)

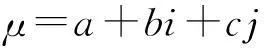
(2)

式(2)为联系数表达式，其中a,b,c∈[0,1]，a+b+c=1.式(1)和式(2)统称为联系数的表达式.联系数的其他表达形式如下：

u=A+Bi，u=a+bi

u=A+Cj，u=a+cj

u=Bi+Cj，u=bi+cj

仅研究u=a+bi+cj联系数的一种特殊形式u=a+bi(c=0)型联系数，并称其为二元联系数，因为二元语义形式的变量可以从不确定性角度用二元联系数来描述，即二元联系数u=a+bi是描述不确定量的一种数，常把a称为确定量，把bi称为不确定量，a和bi统称为二元联系数的联系分量.

针对区间二元语义评价信息的不确定性，下面将从均匀分布考虑区间二元语义评价信息分布的不确定性.

设随机变量X~U(a,b)，则：

(3)

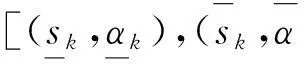
则称之为二元语义联系变量，其中

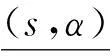
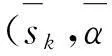
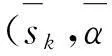
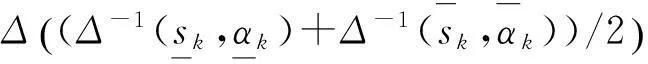
也就是说，在实际的决策过程中，决策者可以根据个人对风险的偏好来选择合适的风险态度因子i，因此对于任意一个区间二元语义变量，它可以表示为含有决策者的风险态度因子i的二元语义联系变量.

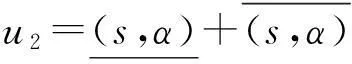
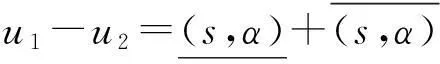
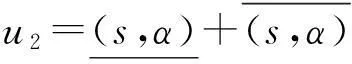
下面考虑将区间二元语义变量看成服从正态分布形式.设随机变量X~N(μ,σ2)，则：

(4)

由式(4)可以看出，基于正态分布的3σ准则，按照原则可以将区间二元语义变量转化为正态分布形式，为此定义二元语义正态分布变量如下：

均方差为

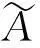
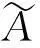
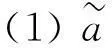
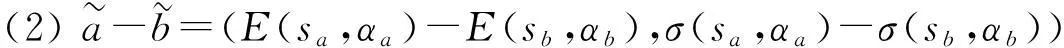
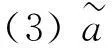
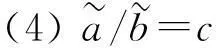
解此方程组得，

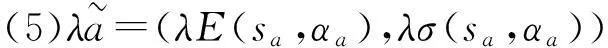
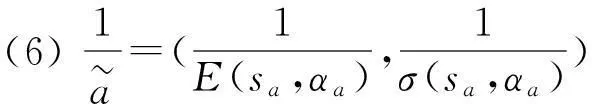
根据期望-方差准则，给出以下一种二元语义正态分布变量的比较与排序方法.

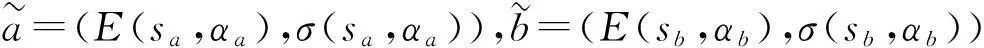
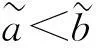
2) 若E(sa,αa)=E(sb,αb)，则：

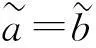
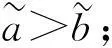
2二元语义联系变量信息集成算子

基于二元语义联系变量的运算法则，下面给出二元语义联系加权算术平均(2TLCWAA)算子的概念.为方便起见，用Ω表示所有二元语义联系变量构成的集合.

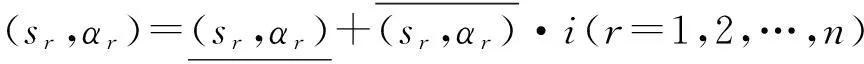
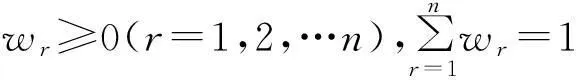
对于2TLCWWA算子含有以下性质：

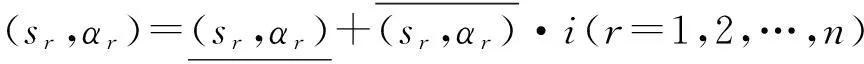
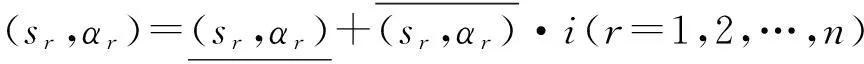
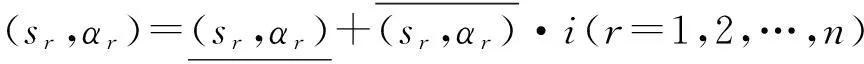
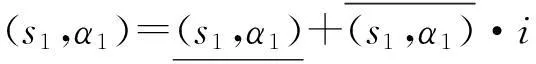
为二元语义联系变量(s1,α1)与(s2,α2)的距离.

同样的，可定义两个二元语义正态分布变量之间的距离

定义9设a1=(E1(s1,α1),σ1(s1,α1))和a2=(E2(s2,α2),σ2(s2,α2))均为二元语义正态分布变量，则a1和a2之间的距离可定义为

3基于二元语义联系变量信息集成算子的区间二元语义多属性群决策方法

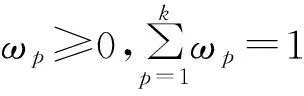
则基于二元语义联系变量信息集成算子的模糊多属性决策方法如下：

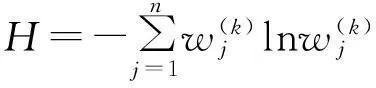
为了达到上述两个目标，求解合理的属性权重w(k)等价于求解如下最优化问题：

(5)

再考虑决策者权重ω=(ω1，ω2,…,ωp)T，则属性的最优权重向量w=(w1,w2,…,wn)T可由下式计算得出：

(6)

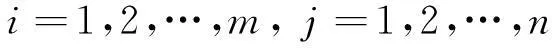
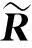
Step 4再次利用2TLCWWA算子

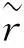
Step 7结束.

4案例分析

某年级准备从3个候选人xi(i=1,2,3)中选拔出最合适的教学办公室主任，评价准则包括工作能力(c1)、学识水平(c2)、服务意识(c3)三个方面.现有3决策者dk(k=1,2,3)，权重向量分别为ω=(0.3,0.4,0.3)T就这三个方面对3位候选人进行考核.预定的语言评价集为S={s0=非常差,s1=很差,s2=差,s3=一般,s4=好,s5=很好,s6=非常好}，3位决策者分别给出其区间二元语义评价信息对这3位候选人给出各项考核评价，结果如下所示，则基于二元语义联系变量算子的模糊多属性群决策方法如下：

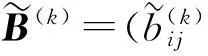
再利用式(6)求得最优属性权重向量为w.

Step 4利用2TLCWAA算子

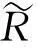
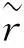
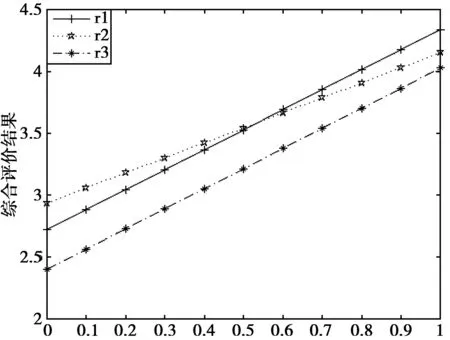
图1　决策者风险态度因子i对综合评价结果s的影响Fig.1　Effect of decision maker risk attitude factori on comprehensive evaluotion result s

由图1可以看出，决策者风险态度因子i对候选人的考核结果有一定的影响，但从数值上影响不大，对总的排名也有一定影响，当i≤0.54时，x1和x2的考核结果相差逐渐减小，但是x2的综合评价结果在决策者非常悲观时，即i≤0.3时明显占优势，而当i>0.54时x1和x2的考核结果相差逐渐增大，但是x1的综合评价结果在决策者非常乐观时，即i≥0.7时明显占优势，而x3的综合评价结果总是处于劣势.也就是说，若决策者非常悲观，可以选择较小的i，此时综合评价结果对x2明显有利，而对于中性或较乐观决策者而言，x1和x2的结果相差不大，两者都可以选择，若决策者非常乐观，可以选择较大的i，此时综合评价结果对x1明显有利，而x3的综合评价结果与其他候选人之间总是保持着一定的差距.

综上所述，考虑决策者的风险态度因子可以得到不同的结果，但是，x3的综合评价结果总是处于劣势，所以x3不纳入考虑当中，而x1和x2的选择需要根据决策者的风险态度因子来做出最后的评价.

下面将二元语义联系变量转换为区间二元语义变量，并运用文献[7,8]中对区间二元语义变量的大小进行比较的方法而构建基于优势度的比较矩阵，得到结果如下：

构建基于两两比较的优势度矩阵，得：

由此得到每个方案的总优势度为

根据总优势度的大小得到排序方案结果为

x2>x1>x3

容易看到方法与文献[7，8]的方法得到的决策结果相似，但与之相比，提出的二元语义联系变量决策方法与以往的区间二元语义决策方法相比，在对二元语义联系变量进行集结时，考虑了决策者的风险态度因子，决策者可以根据自己的乐观状态对二元语义联系变量中的不确定数i进行取值，因此更能反映群决策的决策属性.

5结束语

对属性值为区间二元语义变量而属性权重信息完全未知的多属性决策问题进行了探讨.从区间二元语义变量的分布情况角度入手，定义二元语义正态分布变量、二元语义联系变量，使得区间二元语义变量在一定评价信息范围内的确定与不确定性联系起来，给出了新的信息集成算子，针对属性权重完全未知的情况下，利用二元语义正态分布变量的方差以及属性权重的随机性，通过建立优化模型来确定最优属性权重，进而提出了基于二元语义联系变量的模糊多属性决策方法.方法的优点在于将区间二元语义决策变量通过决策者的风险态度因子转化为二元语义联系变量，使得区间二元语义模糊多属性决策方案排序更为可行和有效.

参考文献(References)：

[1]SENGUPTA A,PAL T K.Fuzzy Preference Ordering of Interval Numbers in Decision Problems[M].Springer Heidelberg Berlin,New York,2009

[2] HERRERA A F,HERRERA EV,MARTINEZ L.A fusion Approach for Managing Multi-granularity Linguistic Term Set in Decision Making[J].Fuzzy Sets and Systems,2000,114:43-58

[3] 晏力，阮艳丽，裴峥.语言值区间二元组能量平均算子及其应用[J].山东大学学报(工学版)，2013，43(1)：115-122

YAN L,RUAN Y L,PEI Z.Linguistic Interval Two-tuple Power Average Operator and Its Application[J].Journal of Shangdong University(Engineering Science),2013,43(1):115-122

[4] 林建，兰继斌，林耀海.基于区间二元语义集结算子的多属性群决策方法[J].吉林师范大学学报(自然科学版)，2007(1)：5-9

LIN J,LAN J B,LIN Y H.A Method of Multi-Attribute Group Decision-Making Based on the Aggregation Operators for Interval Two-tuple Linguistic Information[J].Journal of Jilin Normal University：Natural Science Edition,2007(1):5-9

[5] 王晓，陈华友，刘兮.基于离差的区间二元语义多属性群决策方法[J].管理学报，2011，8(2)：301-305

WANG X,CHEN H Y,LIU X.Multiple Attribute Group Decision Making with Interval Two-tuple Linguistic Information Based on Deviation[J].Chinese Journal of Management,2011,8(2):301-305

[6] 张娜，方志耕，朱建军，等.基于等信息量转换的区间二元语义多属性群决策方法[J].控制与决策，2015，30(3)：403-409

ZHANG N,FANG Z G,ZHU J J,et al.Multiple Attribute Group Decision Making with Interval Two-tuple Linguistic Information Based on the Amount of Information Convert[J].Control and Decision,2015,30(3):403-409

[7] HERRERA A F,MARTINEZ L.A 2-tuple Fuzzy Linguistic Representation Model for Computing with Words[J].IEEE Transactions on Fuzzy Systems,2000(8)：746-752

[8] HERRERA A F,MARTINEZ L.A Model Based on the 2-tules Linguistic for Dealing with Multi-granularity Hierarchical Linguistic Contexts in Multi-expert Decision Making[J].IEEE Transactions on Systems Man and Cybernetics,2001,31:227-234

[9] 赵克勤.集对分析及其初步应用[J].大自然探索，1994，47(13)：67-72

ZHAO K Q.Set Pair Analysis and Its Prelimiary Application[J].Exploration of Nature,1994，13(47)：67-72

[10] YAGER R R.The Power Average Operator[J].IEEE Transactions on Systems Man and Cybernetics,2001,31:724-731

[11] 汪新凡.基于联系数纯语言多属性群决策方法[J].重庆工商大学学报(自然科学版)，2006，23(6)：580-584

WANGXF.Pure-LinguisticInformationMulti-AttributeGroupDecision-MakingMethodBasedonConnectionNumber[J].JournalofChongqingTechnologyandBusinessUniversity(NaturalScienceEdition),2006,23(6): 580-584

[12]XUZS,CAIXQ.UncertainPowerAverageOperatorsforAggregatingIntervalFuzzyPreferenceRelations[J].GroupDecisionandNegotiation,2012(2):1381-397

[13]ZHOULG,CHENHY,LIUJP.GeneralizedPowerAggregationOperatorsandTheirApplicationsinGroupDecisionMaking[J].Computers&IndustrialEngineering,2012,62:989-999

[14]XUYJ,WANGHM.ApproachesBasedon2-tupleLinguisticPowerAggregationOperatorsforMultipleAttributeGroupDecisionMakingUnderLinguisticEnvironment[J].AppliedSoftComputing,2011(11):3988-3997

[15] 林伟.模糊设计方法在功能鞋设计中心的应用[J].包装工程，2015，36(11)：84-87

LINW.ApplicationofFuzzyDesignMethodintheDesignofFunctionalFootnear[J].PackagingEngineering,2015,36(11):84-87

责任编辑：田静

Interval 2-tuple Linguistic Fuzzy Multiple Attributes GroupDecision-making Based on Connection Variables

WU Qun1, WU Peng1, ZHOU Li-gang1,2

(1.School of Mathematical Science, Anhui University, Anhui Hefei 230601, China;2.Signal and Image Processing Institute, Department of Electrical Engineering, University of Southern California, Los Angles, USA)

Abstract：According to the uncertainty of interval 2-tuple linguistic evaluation information, by considering the distribution of interval 2-tuple linguistic variables, the 2-tuple linguistic connection variables and the 2-tuple linguistic normal distribution variables are defined. Their operation laws are studied, and the information aggregation operators of 2-tuple linguistic connection variables are presented. Based on fuzzy multiple attribute group decision-making problem with completely unknown weight of interval 2-tuple linguistic variable attributes of decision-making matrix elements, by using the 2-tuple linguistic variable variance of normal distribution, by constructing optimization model to determine optimal attribute weight, the fuzzy multiple attributes group decision-making method is proposed based on 2-tuple linguistic connection variable information, and finally numerical example is used to analyze the feasibility and validity of this method.

Key words：multiple attribute group decision-making; interval 2-tuple linguistic variable; 2-tuple linguistic connection variable; 2-tuple linguistic normal distribution variable; information aggregation operator

中图分类号：C934

文献标志码：A

文章编号：1672-058X(2016)01-0001-08

作者简介：吴群(1994-)，男，安徽安庆人，硕士研究生，从事预测与决策研究.**通讯作者：周礼刚(1980-)，男，安徽安庆人，副教授，博士，从事预测与决策研究. E-mail:shuiqiaozlg@126.com.

*基金项目：国家自然科学基金(71371011；71301001；11426033);安徽省自然科学基金(1308085QG127；1508085QG149);安徽省振兴计划高校优秀青年人才支持计划项目，安徽大学科研训练计划项目(KYXL2014010);安徽省大学生创新创业训练项目(201510357119).

收稿日期：2015-06-17；修回日期：2015-07-01.

doi:10.16055/j.issn.1672-058X.2016.0001.001