“平均数”的教学要重视其统计意义

陈繁荣



“平均数”的教学要重视其统计意义

陈繁荣

“平均数”的教学，人教版教材原先安排在三年级下册，现移至四年级下册。教材上安排了两个例题，例1是教学平均数的含义和求法，例2是让学生理解比较两组数据的总体情况时，用平均数比较合适。教学目标是：使学生理解平均数的含义，学会简单的求平均数的方法，体会平均数在统计学中的作用，并能够用自己的语言解释其实际意义。

在统计中，算术平均数常用于表示统计对象的一般水平。它是描述数据集中程度的一个统计量，既可以用来反映一组数据的一般情况（用平均数表示一组数据的情况，有直观、简明的特点），也可以进行不同组数据的比较，可以看出组与组之间的差别。用平均数作为一组数据的代表，比较可靠和稳定，它与这组数据中的每一个数都有关系，对这些数据所包含的信息的反映最为充分，因而应用最为广泛，特别是在进行统计推断时有重要作用。求平均数的方法并不难，理解平均数的意义应是本课的重点。教材在习题中安排了不少让学生理解平均数统计意义的题目。这些题目并不单纯是计算平均数，更多的是运用平均数的统计含义解决问题，帮助学生进一步理解平均数的意义。

在平均数中有一种去尾平均数，它是将一组数据中的一个最大值和一个最小值去掉后再求其余数值的平均数。它保留了平均数的集中趋势代表性强的优点，又具有中位数的可排除个别数据变动较大所带来的影响的特点，因而当一组数据的个数较少、且可能个别数据变动较大时，常用去尾平均数描述一组数据的集中趋势。平均数反映一组数据的总体情况比中位数、众数更为可靠、稳定。平均数的缺点是需要整批数据中的每一个数据都加入计算，因此，在数据有个别缺失的情况下则无法准确计算。一组数据的每一个数据都要参加计算才能求出，特别是当一组数据的数量较大时，其计算的工作量也较大。平均数易受极端数据的影响，从而容易让人对平均数产生怀疑。这也就是在许多竞赛中对评委亮分后的成绩分数要去掉一个最高分和一个最低分，再计算平均数的原因。针对这一缺点，教材在练习中以选做题（如下图）的形式让学生在解决问题中有所体会，以进一步丰富学生对平均数特点的认识。

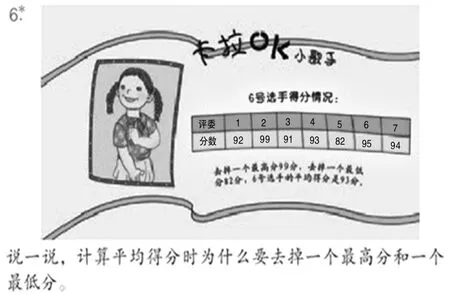
下面是笔者听到的一堂“平均数”教学片段，从中我们可以得到一些启发。

【片段一】

师：（出示分别装有5支、6支和7支笔的3个笔筒）谁能只移动1支笔，使每个笔筒里的笔一样多呢？（指名一位学生上台操作）说说你是怎么想的。

生：从最多的装有7支笔的笔筒里拿出1支放到最少的装有5支笔的笔筒里。

【片段二】

师：你们喜欢什么体育运动？

生：喜欢踢足球、打篮球……

师：下面是两个队进行投篮比赛（每人投10次）投中个数的示意图。你认为哪队的实力强呢？你是怎么知道的？

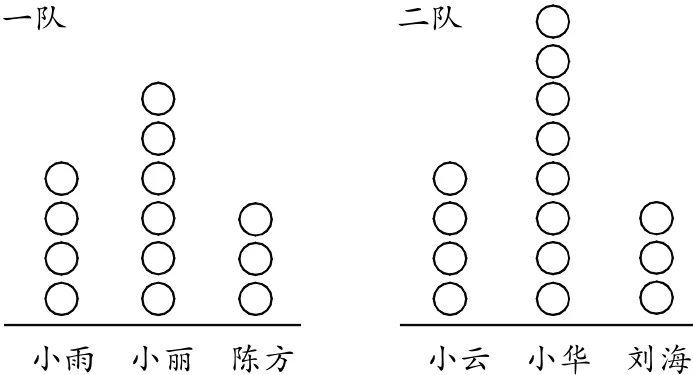
生1：二队的实力强些。因为二队共投中了15个球，一队只投中了13个球。

生2：二队有1个人投中的个数最多。

师：（出示下图）你认为哪队的实力强呢？你是怎么知道的？

生3：四队的实力强，因为四队共投中了16个球，三队只投中了15个球。

生4：不能用总数比较，因为四队多1个人参加比赛。应该是三队的实力强，他们每个人都投中了5个球，四队每个人都只投中4个球。

师：（出示下图）你认为哪队的实力强呢？你是怎么知道的？

学生分组讨论，师指名学生上台操作（如下图所示）。

生5：五队的实力强，平均每个人投中了6个球，六队平均每个人只投中了5个球。

师：你们是怎么算出平均数的？

生6：列式计算。

教材上的例题是小红、小兰、小亮和小明四人一组共收集52个矿泉水瓶，要求平均每个人收集了多少个，内容是采用象形和条形统计图来呈现的。这里的教学片段选择的教学内容是学生投篮比赛，比较两个队的实力强弱，内容的呈现具有层次性，有利于学生的体验与理解、思考与探索。学生通过活动，体会到了学习平均数的必要性和平均数的统计意义，即平均数能较好地反映一组数据的总体情况。遗憾的是活动后教师没有让学生反思。其实，教师可以提问：在人数不相等的情况下怎样比较两队的实力？通过平均数的学习，你感觉到平均数有什么作用？有什么特点？——平均数比这组数据中最大的数要小，比最小的数要大。

（作者单位：攸县酒埠江镇中心小学）