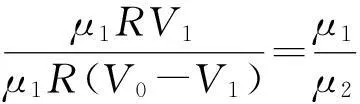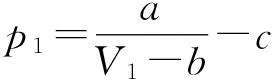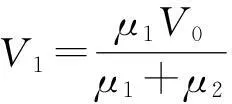对一道“气体类”高考题的讨论
2016-04-15姚黄涛
姚黄涛 冯 杰
(上海师范大学数理学院 上海 200235)
对一道“气体类”高考题的讨论
姚黄涛冯 杰
(上海师范大学数理学院上海200235)
摘 要:2014年全国高考物理上海试卷中第20题,即多项选择题的最后一题,是一道气体类型的题目.自行解题后发现网上相关教师上传的解析存在着不妥之处,于是提供此类型题目的解题方法和相应结论以供参考.
关键词:高考物理理想气体
1原题与参考答案
原题[1]如下:如图1,在水平放置的刚性气缸内用活塞封闭两部分气体A和B,质量一定的两活塞用杆连接,气缸内两活塞间保持真空,活塞与气缸壁之间无摩擦,左侧活塞面积较大,A,B的初始温度相同,略抬高气缸左端使之倾斜,再使A,B升高相同温度,气体最终达到稳定状态.若始末状态A,B的压强变化量ΔpA,ΔpB均大于零,对活塞压力的变化量为ΔFA,ΔFB,则
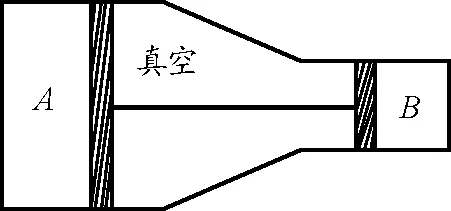
图1
A.A体积增大B.A体积减小
C.ΔFA>ΔFBD.ΔpA<ΔpB
此题标准答案为A,D.
参考答案[2]如下:
平放时有
pASA=pBSB
由SA>SB得
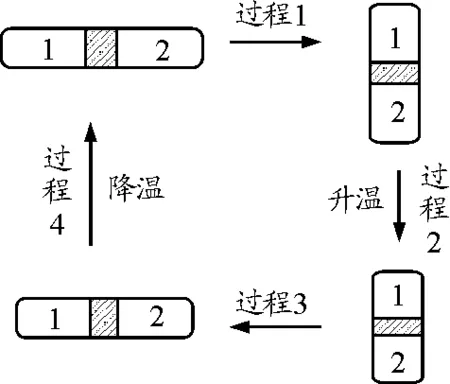
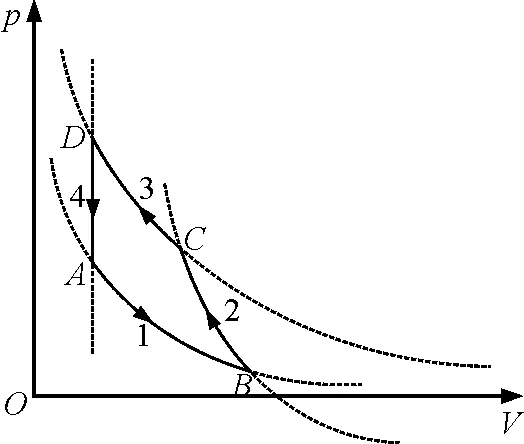
pA (1) 倾斜后一定有 (pA+ΔpA)SA+(M+m)gsinθ= (pB+ΔpB)SB (2) 升温后先假设A,B体积均不变,由查理定理有 (3) 故D正确. 故ΔFA=ΔFB (4) 如果活塞质量忽略不计,则前后两个状态活塞不动,A,B体积均不变,现在活塞有了质量故活塞会向下滑,即A体积增大.” 2分析题目和“参考解析”中的问题 整个系统发生了两个过程,先将气缸左端抬高,后升高温度,题目所要问的是两个过程前后A,B气体的物理量的变化,即状态参量的改变量.对于判断ΔpA与ΔpB的关系,参考答案中式(3)得出的结论是ΔpA<ΔpB,我们注意到得出此结论的基础是假设A,B气体的体积不变,但是实际情况是求A,B气体经过两个过程后压强总的改变量,其中体积显然是发生变化的,那么体积的变化会引起压强的变化,所以直接用查理定律的变式解决Δp不合适(此方法常常适用于判断两部分封闭气体之间水银柱的移动方向,我们要搞清楚这两种情况的区别,以防思维定势的误导),同样的道理,式(4)得出的结果也存在方法上的问题.最后再看判断气体A的体积变化的分析,参考答案未考虑升高温度所产生的影响,同时其判断方法模糊不清,无法触及到此类问题的本质所在. 现分析如下:设活塞总体质量为m,左端抬高为过程1,加热为过程2,A,B气体状态参量分别用pA,pB,VA,VB表示,初始状态参量分别为pA0,pB0,VA0,VB0.当气缸平放时有pA0SA0=pB0SB0,经过过程1和过程2后系统处于平衡,则 (pAO+ΔpA)SA+mgsinθ=(pBO+ΔpB)SB (5) ΔpASA+mgsinθ=ΔpBSB (6) ΔFA+mgsinθ=ΔFB (7) 所以 ΔFA<ΔFBΔpA<ΔpB 对于A体积如何变化,我们分开考虑.过程1中,A的体积增大,活塞右移;过程2中,假设升高温度时活塞不发生移动,根据查理定律有 (8) 所以 则活塞将左移,A的体积在过程2中会减小.于是我们发现无法以此判断A的体积的总变化. 3引入物理模型得出两个结论 图2 我们考虑以下物理模型——两端封闭玻璃管中上下部分被水银柱隔开的气体,如图2所示.设上部分气体1和下部分气体2的状态参量分别为 p 1 , V 1 和 p 2 , V 2 ,水银柱产生的压强为 p 0 ,气体1和气体2的总体积为 V 0 .则 p1+p0=p2 (9) p1V1=μ1RT (10) p2V2=μ2RT (11) V1+V2=V0 (12) 由式(9)、(10)、(11)、(12)消去p1,p2,得出上部分气体体积与温度的关系 (13) 对于式(13),当T→∞时,两边取极限 当p0→0时(即管子水平放置),两边取极限 也就是说,将管子转至水平位置与将温度升高至无穷大,两者的效果是相同的,即水银柱处于同一位置.或者换一种说法,我们的第一个结论是:水平放置的管子被竖直后,上部分气柱体积增大,若想使其体积减小到原来的程度,则需将气体的温度升高到无穷大.更进一步,这里的p0可以看成非竖直情况下水银柱产生压强的竖直分量,那么在有限的温度范围内,无法通过升温消除力学影响(这里仅限于我们讨论的图2所示的物理模型). 对于图2中的上部分气体1,由式(13)和理想气体物态方程p1V1=μ1RT,消去变量T后可以得出封闭管子中上部分气体在温度变化过程中,压强与体积的关系 μ2RTV1=(μ1RT+p0V1)(V0-V1) (14) 于是我们进一步分析下图2中上部分气体1所经历的一个循环过程,此循环过程可以分为4个阶段,如图3.玻璃管由水平转至竖直方向为阶段1;对玻璃管上下部分气体加热为阶段2;玻璃管由竖直转动至水平方向为阶段3;对玻璃管降温至初始温度为阶段4.将这4个过程作于p-V图像上,如图4所示.(注意:研究对象为上部分气体1) 图3 图4 4总结 归纳得出的两个结论: (1)水平放置的管子被竖直后,上部分气柱体积增大,若想使其体积减小到原来的程度,则需将气体的温度升高到无穷大. (2)理想气体从初状态经过一系列过程最终达到的末状态是唯一的,无关乎这些过程的顺序. 回到2014年的那道高考题,根据结论(1),可以判断出|ΔV1|<|ΔV1|,所以最终A的体积是增大的.从本质上看,如果气缸左端未抬高,只是升温,那么活塞是不会移动的,即过程1中活塞的移动是过程2中活塞移动的原因,体积增大的效应是大于体积减小的效应的,或者说升温引起的体积减小无法补偿左端抬高引起的体积增大.从结论(2)出发,我们也可以得出那道高考题的A选项,整个系统经历了两个过程,由于理想气体的状态变化与过程无关,那么系统的末状态的确定就无关乎这两个过程的先后顺序,所以我们可以假设先升温,后将左端抬高,这样的话,我们很容易地可以得出VA最终是增大的. 参 考 文 献 12014年全国高考物理上海试卷及答案详解. (收稿日期:2015-08-31)