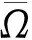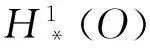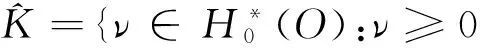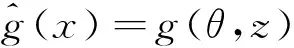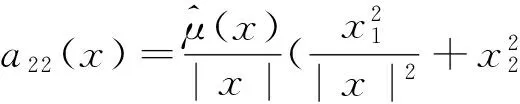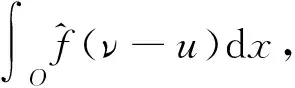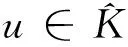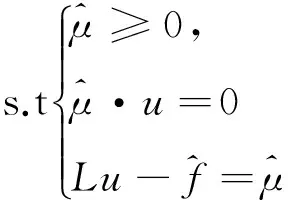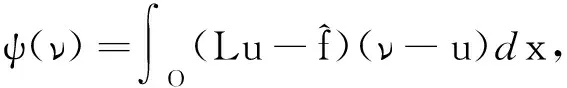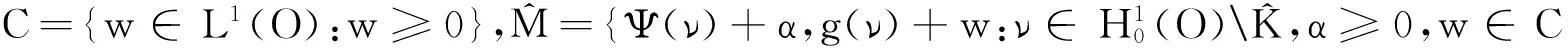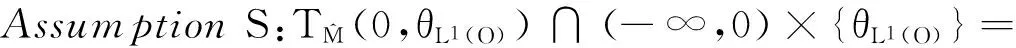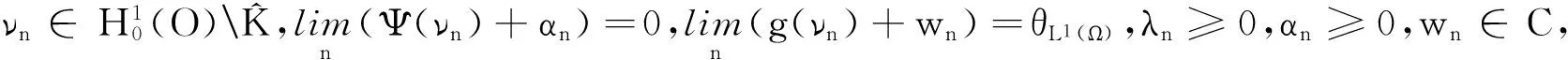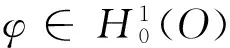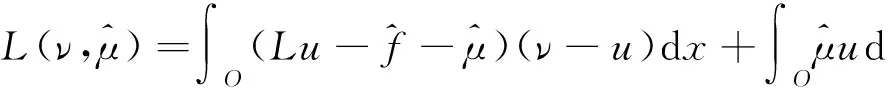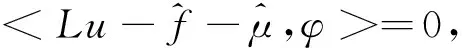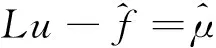无限维空间中强对偶定理在润滑问题上的应用*

邬月月，胡艳红

(哈尔滨师范大学)

无限维空间中强对偶定理在润滑问题上的应用*

邬月月，胡艳红

(哈尔滨师范大学)

研究在无限维空间中，强对偶定理在润滑问题上的应用，并找到了润滑问题的对偶问题的无限维lagrange乘子.

强对偶定理;润滑问题;lagrange乘子

0 引言

该文主要研究的是介于无限维凸优化问题和它的lagrange对偶问题之间的强对偶定理及其它的应用.文献[1]中，作者通过假设 给出无限维空间中凸优化问题的强对偶定理，并把它应用到双障碍问题上.在文献[2]中，作者研究了强对偶定理在弹缩扭转问题上的应用.以上作者是把这些实际问题转换成变分不等式，进而转化为无限维凸优化问题，再应用强对偶定理找到研究问题的对偶问题的无限维lagrange乘子.

笔者研究的问题是一个完整轴颈轴承的润滑剂薄膜的压强分配问题，所以说这是一个力学问题中的润滑问题[3].主要结果是把强对偶定理应用到这个力学问题上.通过把原问题转变成变分不等式，再把强对偶定理应用到变分不等式上，同时找到了原问题的对偶问题的无限维lagrange乘子.

1 预备知识

定义1[1]X是线性拓扑空间,Y是由赋序锥C定义的实赋范空间,Z是实赋范空间,S是X的一个凸子集.f是S到X的给定泛函，g是S到Y的映射，考虑的约束集合是K={x∈S:g(x)∈-C}.

该文研究的优化问题为：找到x0∈K,使得

(1)

通常它的Lagrange对偶问题为：

(2)

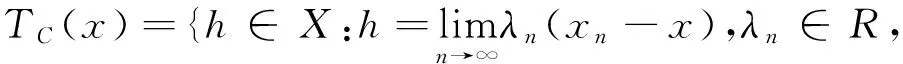
定义3[2]假设S在一点x0∈K满足是指

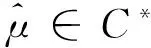
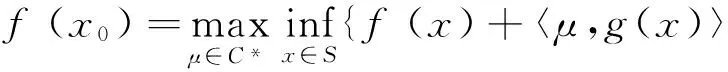
推论5[2]如果问题(1)与问题(2)之间的强对偶成立，那么假设S也是满足的.

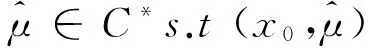
2 主要内容

文献[4]中的润滑问题可以写成以下变分不等式

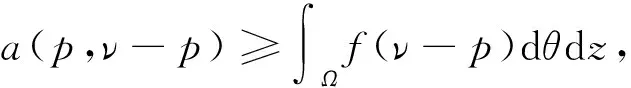
(3)

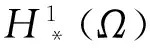
ν(0,z)=ν(2π,z),|z|

ν(b,θ)=ν(-b,θ)=0,0≤θ≤2π.

Ω={(θ,z):0<θ<2π,|z|

这里提到的ω,η,ε都是文献[3]中润滑问题提到的变量.

x1=(a+b+z)cosθ,x2=(a+b+z)sinθ,令x=(x1,x2)

则O={x∈R2:a<|x|

问题(3)可等价的表示为如下变分不等式问题：

(4)

(5)

(6)

下面给出该文研究的主要结果：

(7)

(-φ)dx≥0.

另一个方向，要证假设S成立，下面让(7)式成立，所以有

故假设S成立，综上所述，定理得到证明.

[1] Evans L C. The infinite dimensional Lagrange multiplier rule for convex optimization problems[J].Journal of Functional Analysis,2011(261):2083-2093.

[2] Daniele P, Maugeri A,Raciti F.Duality Theory and Applications to Unilateral Problems[J],J Optim Theory Appl,2014,162:718-734.

[3] David Kinderlehrer,Guido Stampacchia.An Introduction to Variational Inequalities and Their Applications. Springer in Applied Mathematics, New York, 1980.

[4] Mauger A,Puglisi D. A new necessary and sufficient condition for the strong duality and the infinite dimensional Lagrange multiplier rule[J]. J Math Anal Appl, 2014,415:661-676.

(责任编辑：季春阳)

Strong Duality Theory on Application of Lubrication Problem in Infinite Dimensional Space

Wu Yueyue, Hu Yanhong

(Harbin Normal University)

In this paper, concerned with the problem in infinite dimensional space, strong duality theory of the lubrication problem are applied and the dual problem of the lubrication problem and its infinite dimensional lagrange multiplier are found.

Strong duality theory; The lubrication problem; Lagrange multiplier

2016-12-23

*黑龙江省教育厅项目(12521147)

O189

A

1000-5617(2016)05-0013-03