最小二乘估计的性质
2016-04-15陈佳妮
陈佳妮
(哈尔滨远东理工学院)
最小二乘估计的性质
陈佳妮
(哈尔滨远东理工学院)
估计线性模型中的回归参数的基本方法就是最小二乘法,鉴于最小二乘估计在实际生活中的作用及其地位,就最小二乘估计的性质进行分析.
线性模型;最小二乘估计;性质
0 引言
经典线性回归模型[1]自创立以来,无论是在医学,还是在科研中,亦或是实践中都得到了广泛的应用,并取得了相当大的成果.线性回归模型中的回归系数的估计问题一直是众多学者研究分析的课题,其中最原始也是最基本的估计方法就是“最小二乘估计”[2].最小二乘法是一种数学优化技术,又称作“小平方法”,它通过最小化误差的平方和寻找数据的最佳函数匹配,以达到最终解决问题的目的.作为回归参数估计的最基本方法,最小二乘估计在统计学、计算数学、运筹学以及控制论中都占有重要的地位.该文主要介绍最小二乘估计的基本方法,并对最小二乘估计的性质[3]进行研究.
1 最小二乘估计的原理
首先给出一个线性模型.因变量Y与对其有影响的m个自变量X1,X2,…,Xm具有如下的线性关系[4]:
Y=β0+β1X1+…+βmXm+ε

yi=β0+β1xil+…+βmxim+εi,i=1,2,…,n
其矩阵形式为:

将此矩阵简化等价于:
Y=Xβ+ε
那么估计参数β的最基本方法就是最小二乘法,其原理为使得‖Y-Xβ‖2达到最小,通过求偏导[5]得到参数估计:
2 最小二乘估计的性质
最小二乘估计具有很多优良的性质,正是因为如此,奠定了其在回归参数估计中的地位,本节主要介绍其几个重要性质.

(X′X)-1X′E(Y)=(X′X)-1X′Xβ=β
证毕.
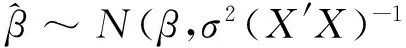

(X′X)-1X′Cov(Y)((X′X)-1X′)′=(X′X)-1X′XCov(Y)(X′X)-1=σ2(X′X)-1.
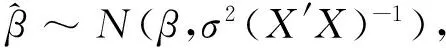
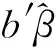

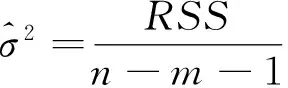
证明 因为残差平方和
E(RSS)=(n-m-1)σ2
那么
E(RSS)=E(Y′(I-X(X′X)-1X′)Y)=β′X′(I-X(X′X)-1X′)Xβ+tr((I-X(X′X)-1X′)σ2)=0+tr((I-X(X′X)-1X′)σ2)=(n-(m+1))σ2.
证毕.
3 结论

[1] 王松桂.线性统计模型[M].合肥:安徽教育出版社,1987.
[2] 陈希孺,王松桂.线性模型中的最小二乘法[M].上海:上海科技出版社,2003.
[3] 陈希孺.最小二乘估计相合性的若干结果[J].科学通报,1994,39(13).
[4] 陈希孺.数理统计引论[M].北京:科学出版社,1981.
[5] 韩兆洲,汪建华.线性化最小二乘法的理论分析[J].统计与决策,2009(10):29-30.
[6] 秦峰.广义Gauss-Markov模型参数的Bayes线性无偏估计及优良性研究[]J.重庆大学,2013(9):1-7.
[7] 张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1983.
(责任编辑:于达)
The Nature of the Least Squares Estimate
Chen Jiani
(Harbin Far East Institute of Technology)
The based method of estimating regression parameters of the linear model is the least squares estimate,according to its role and status in real life,analysis of the nature of the least squares estimate will be performed in this paper.
Linear Model;Least Squares Estimate;The Nature
2016-05-05
O212
A
1000-5617(2016)05-0007-02
