二元上尾独立风险模型中的带有随机权重的随机变量的大偏差*
2016-04-15陈丽莹
陈丽莹
(内蒙古民族大学)
二元上尾独立风险模型中的带有随机权重的随机变量的大偏差*
陈丽莹
(内蒙古民族大学)
设{Xi,i≥1}是一个二元上尾独立的服从不同分布的随机变量,{θi,i≥1}是一个独立同分布的非退化的随机变量,研究了由{Xi,i≥1}和{θi,i≥1}构成的风险模型中的大偏差,采用类似求带随机权重的相依风险模型中的大偏差的方法,得到了二元上尾独立风险模型中的带有随机权重的随机变量的大偏差的一致渐近公式.
随机权重;大偏差; 二元上尾独立
0 引言
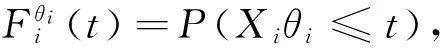
记模型
(1)
称(1)为一个带有随机权重的非随机和.见文献[1-3].
当θi退化到1时,带有随机权重的随机和退化到一般的随机变量和.见文献[4-8].
1 预备知识
定义1 如果不存在指数矩,即对EetX,∀t>0不存在,则称某一非负随机变量X或者其分布F(X)是重尾的.
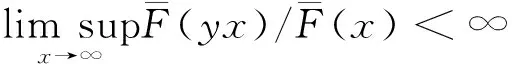
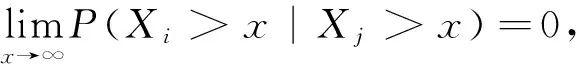
引理1 设{Xi,i≥1}满足BUTI的,且Fi,i≥1服从D族;有{θi,i≥1}满足P(a≤θ≤b)=1,其中(0 证明 接下来给出该文要用到的三个假设条件,如下: 假设条件1 存在非负的随机变量X和某个正数M0,X的分布函数F(x),{Xi,i≥1}和X满足:对于∀n∈Z+,有 假设条件2 存在非负随机变量Y和某个正数M1,Y的分布函数G(x),Y的数学期望存在,{Xi,i≥1}和Y满足:对于∀x>0和∀n∈Z+,有(见文献3) 假设条件3X和Y是尾等价的,即 证明 对任意的0<η<1,有 由于 任意的0<δ<1由假设条件可得 所以有 L2≥(1-δ)P(S(1-η)λ(t)-(1-η)μθλ(t)>x+μθλ(t)-(1-η)λ(t)μθ) 又由定理1可得: 从上式可导出 从而有 故结论成立. 上述定理对不同分布的尾概率做了加权推广,得到了加权随机和的大偏差的结论. [1] Tang Qihe, Tsitsiashvili G. Randomly weighted sums of subexponential random variables with application to ruin theory[J]. Extremes, 2003, 6: 171-188. [2] Wang Dingcheng, Tang Qihe. Tail probabilities of randomly weighted sums of random variables with dominated variation[J]. Stochastic Models,2006,22:253-272. [3] Zhang Yi, Shen Xinmei, Weng Chengguo. Approximation of the tail probability of randomly weighted sums and applications [J]. Stochastic Processes and their applications, 2009, 119: 655-675. [4] 华志强,杨少华,陈丽莹.上尾渐近独立随机变量和的大偏差的渐近下界[J]. 数学杂志, 2014, 34(1): 58-64. [5] 华志强,宋立新,冯敬海,齐晓梦. 索赔盈余风险模型中精确大偏差[J]. 大连理工大学学报, 2016, 56(1): 64-69. [6] 华志强,玄海燕,董莹,等. 一个宽上限相依不同分布的随机变量和不等式[J]. 兰州理工大学学报, 2016, 33(2): 151-153. [7] 华志强,张春生. 推广的延拓负相依风险模型中的精确大偏差[J]. 重庆师范大学学报:自然科学版, 2016,42(1):62-66。 [8] Hua Zhiqiang, Song Lixin, Lu Dawei, et al. Precise large deviations for the difference of two sums of END random variables with heavy tails[J]. Communications in Statistics-Theory and Methods,2017,46(2):736-746. (责任编辑:季春阳) Large Deviation with Random Weight Random Variables in Bivariate Upper Tail Independent Risk model Chen Liying (Inner Mongolia University for the Nationalities) Let {Xi,i≥1} be a sequence of bivariate upper tail independent and non-identically distributed random variables, and {θi,i≥1} be a sequence of independent identically distributed random variables random variables. In this paper, the large deviation in a risk model is investigated, which is constructed by {Xi,i≥1} and {θi,i≥1}, and the asymptotic formula of the large deviation is obtained by using the method of large deviation in a risk model, which is constructed by dependent and random weighted random variables. Random weight; Large deviation; Bivariate upper tail independence 2016-12-15 *内蒙古民族大学科学研究基金资助项目(NMDYB1437) O2111 A 1000-5617(2016)05-0005-02
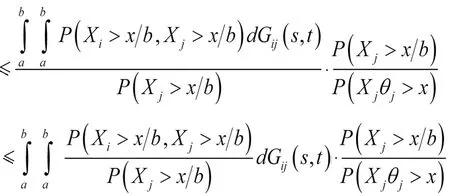

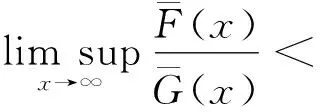
2 非确定和的精确大偏差