基于LS-DYNA软件的爆索空中弹道仿真研究*
2016-04-15万业廷高建光
万业廷 高建光
(1.海军工程大学 武汉 430033)(2.92196部队 青岛 266200)
基于LS-DYNA软件的爆索空中弹道仿真研究*
万业廷1高建光2
(1.海军工程大学武汉430033)(2.92196部队青岛266200)
摘要在应用火箭弹外弹道理论、确定爆索拉出前初始弹道参数的基础上,文章使用LS-DYAN软件建立了弹仓、爆索以及发动机段的有限元模型,定义并加载了气动载荷和初始条件,仿真了爆索空中拉出下落的运动轨迹。计算结果直观、精确,为此类弹道的研究提供了新的基于有限元平台的仿真思路。
关键词爆索; LS-DYAN软件; 空中弹道
Simulation of Blasting-Rope Air Trajectory Based on LS-DYNA Software
WAN Yeting1GAO Jianguang2
(1. Naval University of Engineering, Wuhan430033)(2. No. 92196 Troops of PLA, Qingdao266200)
AbstractBased on the rocket exterior ballistics and the initial trajectory parameters of blasting-rope, this paper builds the finite element models of the magazine, blasting-rope and rocket engine by LS-DYNA software, defines and loads the pneumatic load and initial conditions, simulates the movement locus of blasting-rope. The calculation results are intuitionistic and accurate, which provides a new simulation method for this type of trajectory based on finite element platform.
Key Wordsblasting-rope, LS-DYNA software, air trajectory
Class NumberTJ012.3
1引言
为了实现远距离快速爆破敌方滩头雷区和障碍,本文设想一种尾翼式不旋转爆破火箭弹,该火箭弹主要由弹仓、爆索以及发动机段三部分构成,其中爆索由一定长度的连接绳和球形子弹串接组成。其主要作战过程为火箭弹发射至预定空域后,弹仓和发动机段在燃气活塞作动下迅速分离,形成速度差,而爆索则利用发动机段与弹仓的相对速度以及发动机段本身气动阻力实现空中展开拉直并最终呈“一”字形落地起爆,如图1所示。
要想实现上述战术想定,关键是实现爆索空中迅速拉出并呈“一”字形落地,这需要准确计算爆索的空中弹道轨迹,确定合适的分离点和相对分离速度。传统的火箭弹弹道计算,理论模型已经非常完善[1~7],但是上述爆索分离展开的弹道轨迹研究目前则相对少见,而直接的建模方式仍是参考火箭弹外弹道模型,利用Matlab软件进行仿真[3],不够直观,而且连接绳的折叠以及展开无法精确建模。因此,本文探索应用有限元软件平台LS-DYAN[8~11],进行爆索空中弹道轨迹的仿真计算。
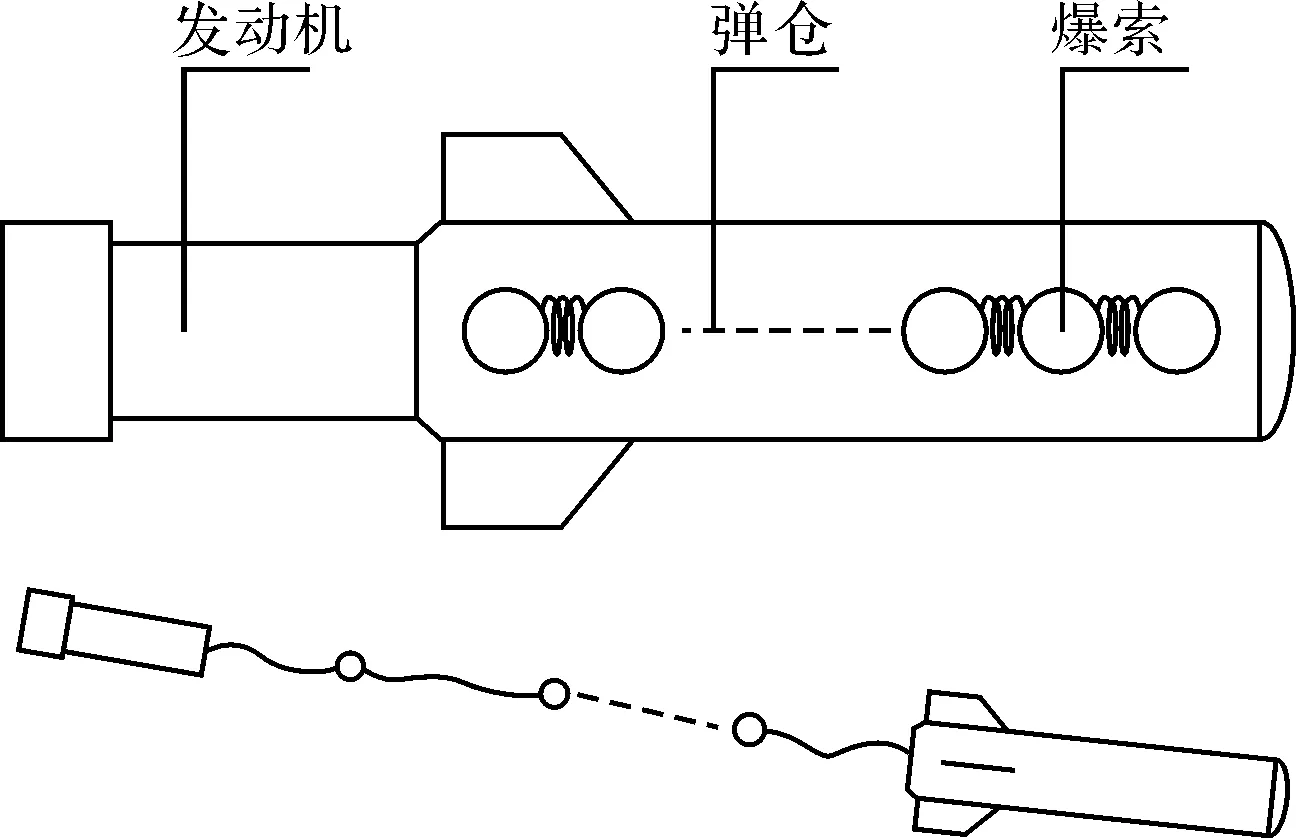
图1 爆破火箭弹结构及爆索展开图
本文首先应用传统的火箭弹外弹道理论[1],建立了射击平面内外弹道运动微分方程组,并应用Matlab软件仿真了分离前火箭的运动轨迹,确定了爆索展开前的弹道参数。随后,应用LS-DYAN软件建立了有限元仿真模型,定义并加载了气动载荷和初始条件,仿真分析了爆索空中展开下落的运动轨迹。
2分离前火箭外弹道计算
为准确计算爆索空中拉出时弹仓、子弹以及发动机段的初始弹道参数,本节在分析火箭弹空中运动过程中弹体所受气动力和气动力矩情况的基础上,建立了射击平面内五自由度刚体运动微分方程[1~2],并通过Matlab进行了数值仿真计算,最后研究了燃气活塞作动分离后弹仓、爆索以及发动机段相对速度的估算方法。
2.1作用在弹体上的气动力和气动力矩
火箭弹在射击平面内的受力情况如图2所示。假设火箭弹小攻角条件下飞行,发动机推力曲线已知,忽略非定常运动附加质量和质量惯性矩的影响,弹体所受气动力和气动力矩的表达式如下[1~2]:
空气阻力:
(1)
空气升力:
(2)
稳定力矩:
(3)
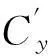
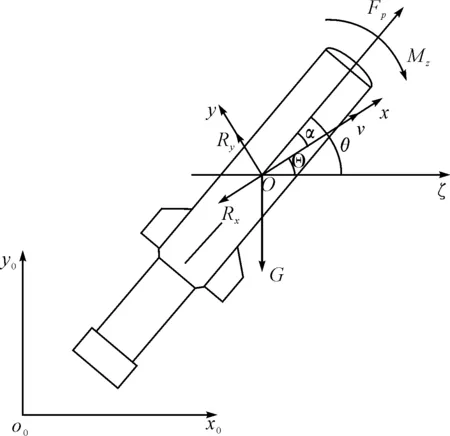
图2 火箭弹受力及运动平面图
2.2运动微分方程的建立与仿真
由动量定理和动量矩定理可知,火箭弹射击平面内外弹道运动微分方程组由质心平面运动方程、弹体平面运动方程以及弹体绕轴转动方程组成[1],其中质心运动方程在地面坐标系o0-x0y0中建立,坐标原点位于发射点处,x0y0平面与射击平面重合,o0x0轴指向发射方向;弹体平面运动方程以及弹体绕轴转动方程在速度坐标系o-xy中建立,坐标原点位于弹体质心处,xy平面与射击平面重合,速度v位于射击平面内,ox轴与速度方向一致。火箭弹在射击平面内的运动如图2所示。
弹体平面运动方程:
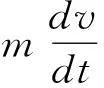
(4)
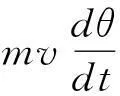
(5)
弹体绕轴转动方程:
(6)
dθ/dt=ω
(7)
弹体质心运动方程:
(8)
(9)
式中,Fp为发动机推力,a为攻角,θ为弹道偏角,Θ为弹道角,ω为弹体绕质心轴的转动角速度。根据攻角、弹道偏角以及弹道角的几何关系,可知:
a=θ-Θ
(10)
综和方程(1)~(10),得到了火箭弹射击平面内五自由度运动微分方程组,在给定初始条件的情况下,运用Matlab软件中的龙格-库塔函数[3~4]进行数值计算,结果如图3所示。
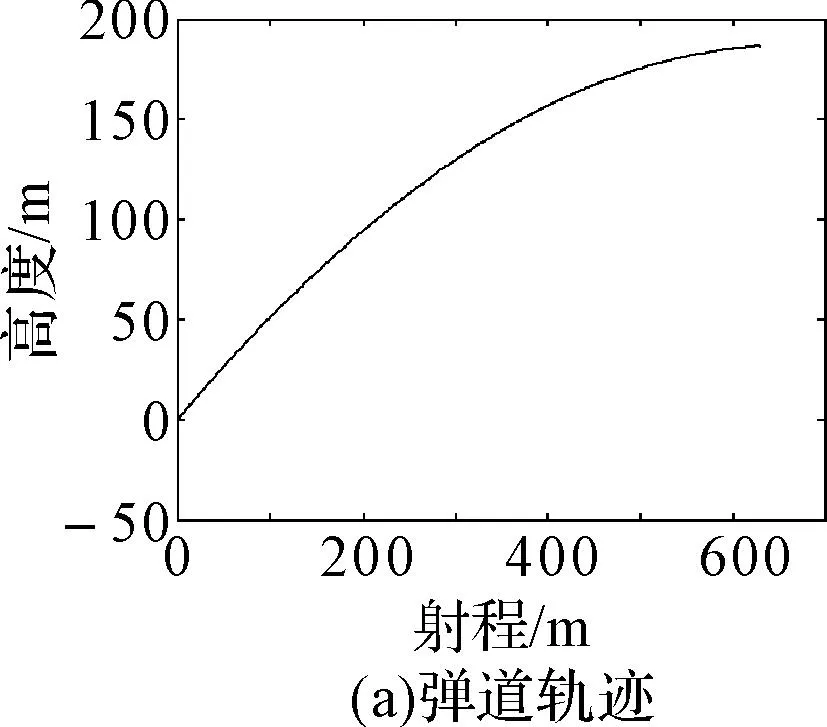
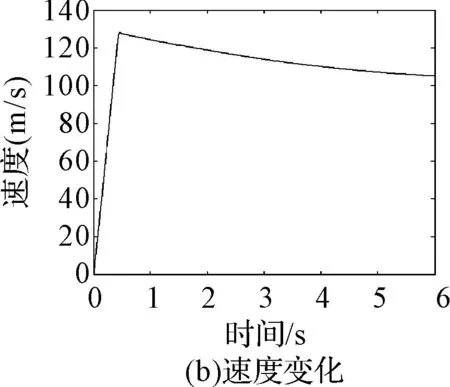
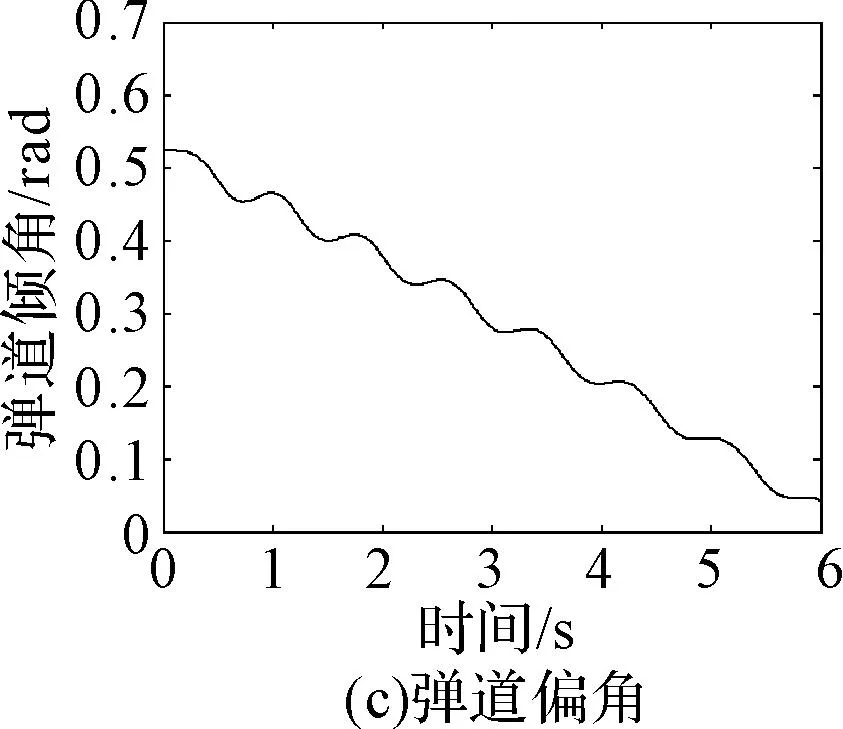
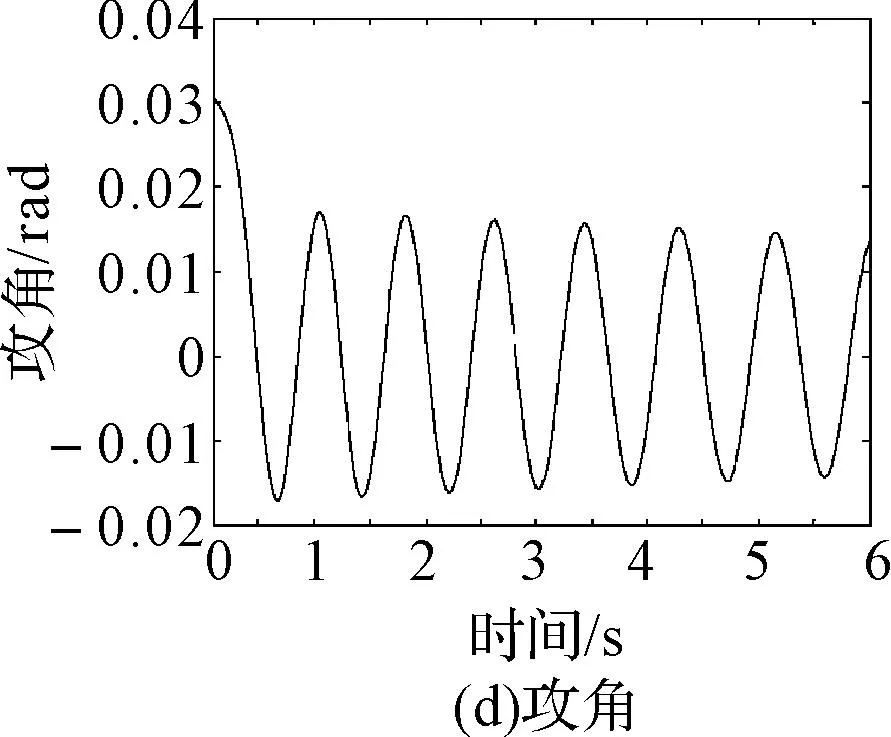
图3 火箭弹分离前外弹道分析图
2.3燃气作动分离相对速度的估算
火箭弹采用燃气活塞作动的方式在时间延时装置的控制下进行分离。由于燃气作动分离时间极短,一般为几毫秒至几十毫秒[8],在这个过程中,忽略弹体气动阻力的影响,可以认为整个火箭弹动量守恒,燃气活塞相互作用力为内力,这样发动机段减速,弹仓以及爆索加速,两者之间形成速度差,利用发动机段的速度差及其本身的气动阻力,可以实现爆索的拉出展开,最后呈现“一”字型落地起爆。假设分离前火箭弹的运动速度为v0,弹仓、爆索以及发动机段的质量分别为mc、ms以及mr,根据动量守恒定律:m·v0=(mc+ms)·vc+mr·vr,在已知速度差的情况下,可以计算得到分离后的各部件速度。
计算得到相对速度之后,忽略作动分离极短时间内的弹道变化,则根据2.2节的仿真结果,可以明确火箭弹分离后,即爆索空中拉出前的位置、速度、角速度、弹道偏角以及攻角等弹道参数,这些参数将作为初始条件,加载到下一节中的仿真模型中,用于后续爆索展开下落弹道轨迹的计算。
3仿真模型的建立
火箭弹燃气作动分离后,其结构可简化为由弹仓、爆索(子弹和连接绳)以及发动机段三部分组成,本节首先建立火箭弹分离时刻弹仓、爆索以及发动机段的有限元模型,然后定义并施加推力、重力、气动力和气动力矩等载荷曲线,最后加载上一节中计算的弹道初始条件、设置控制参数,并进行仿真计算。
3.1有限元模型的建立
根据火箭弹各组成部分的结构尺寸,首先建立几何模型,然后分别进行网格划分。弹仓、子弹以及发动机段进行四面体单元网格划分;连接绳进行离散梁单元网格划分[9]。
网格划分完毕后,需要进行单元算法的选择和材料属性的定义[10]。在LS-DYNA软件中,利用关键字*SECTION_SOLID对弹仓、子弹以及发动机段的体单元选择中心单点积分常应力体单元算法公式[8];而子弹之间的连接绳则利用关键字*SECTION_BEAM选择离散梁单元算法公式。单元算法设置完毕后,进行材料属性的定义。弹仓、子弹以及发动机段视为刚体,利用关键字*MAT_RIGID分别设置体单元材料密度、刚度以及泊松比等参数;而连接绳则利用关键字*MAT_CABLE进行离散梁单元的密度、刚度、泊松比以及预应力等参数的定义[11]。
完成上述步骤后,爆索展开前的有限元模型即建立完毕,下一步需要定义载荷曲线并进行加载。仿真模型如图4所示。
3.2载荷曲线的定义与加载
在爆索展开下落过程中,弹仓、子弹以及发动机段分别受气动阻力、升力、气动力矩以及重力的作用,需要根据计算公式定义载荷曲线[8],并分别施加到弹仓、子弹以及发动机段上。

图4 爆索拉出前有限元模型简图
首先定义重力曲线并加载。根据各个刚体的实际质量利用关键字*DEFINE_CURVE定义重力常量曲线,然后利用关键字*LOAD_RIGID_BODY施加到各个刚体的重力方向上。其次定义气动阻力、升力以及气动力矩函数曲线并加载。根据式(1)~式(3),利用关键字*CURVE_FUNCTION中的库函数[11],可以计算弹仓、子弹以及发动机段刚体的速度、角速度和攻角等参数,然后定义各个刚体的阻力、升力以及力矩函数曲线,最后利用关键字*LOAD_RIGID_BODY施加到弹仓、子弹以及发动机段上,如图5所示。
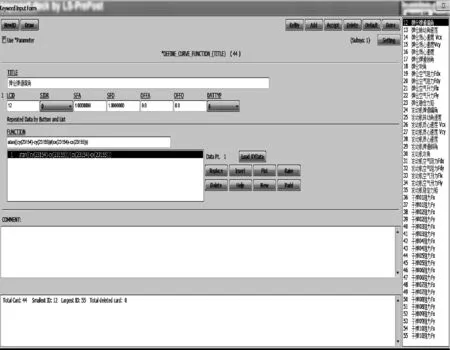
图5 载荷曲线定义加载界面
3.3初始条件的施加
载荷曲线定义及施加完毕后,根据第一节中计算得到的分离时刻的弹道参数,对弹仓、爆索以及发动机段施加初始条件。首先,平移有限元模型至分离点的位置,然后旋转模型,调整至分离时刻的弹道偏角,最后利用关键字*INITIAL_VELOCITY给弹仓、爆索以及发动机段施加初始速度ox轴和oy轴分量以及角速度[8~9]。
初始条件施加完毕后,设置求解控制参数。主要包括关键字*TERMINATION、*TIMESTEP计算时间和时间步长的设置,关键字*DATATBASE_BINARY_D3PLOT、*ASCII_OPTIPN文件格式和载荷曲线的输出设置等。
最后导出仿真模型的关键字文件,在LS_DYNA软件的求解器中进行并行计算,并对求解过程进行监控。
4仿真结果分析
经过仿真计算,爆索空中拉出下落的弹道轨迹,如图6所示。


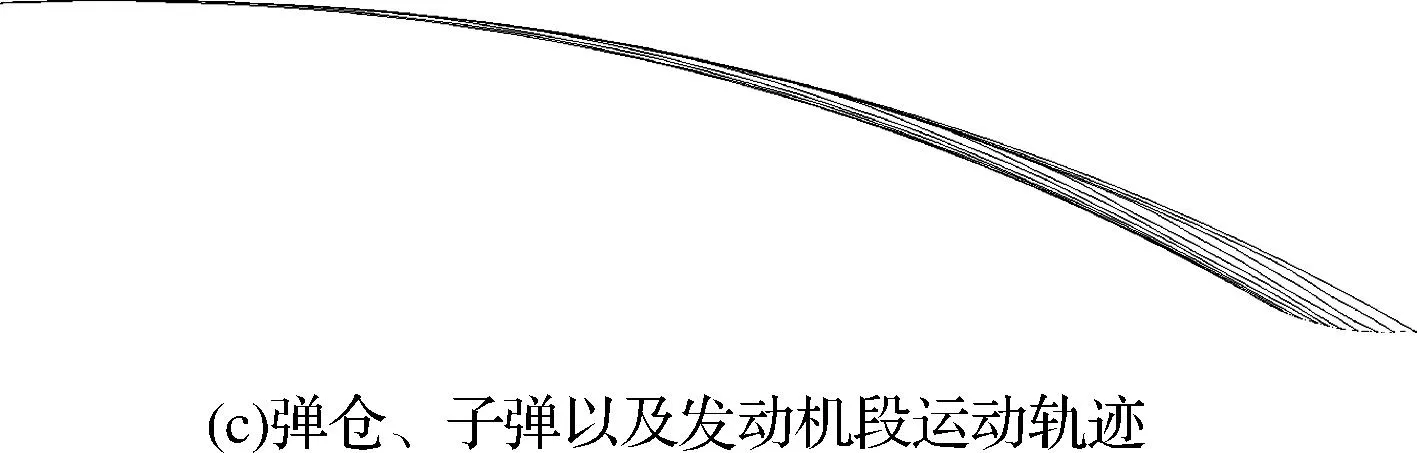
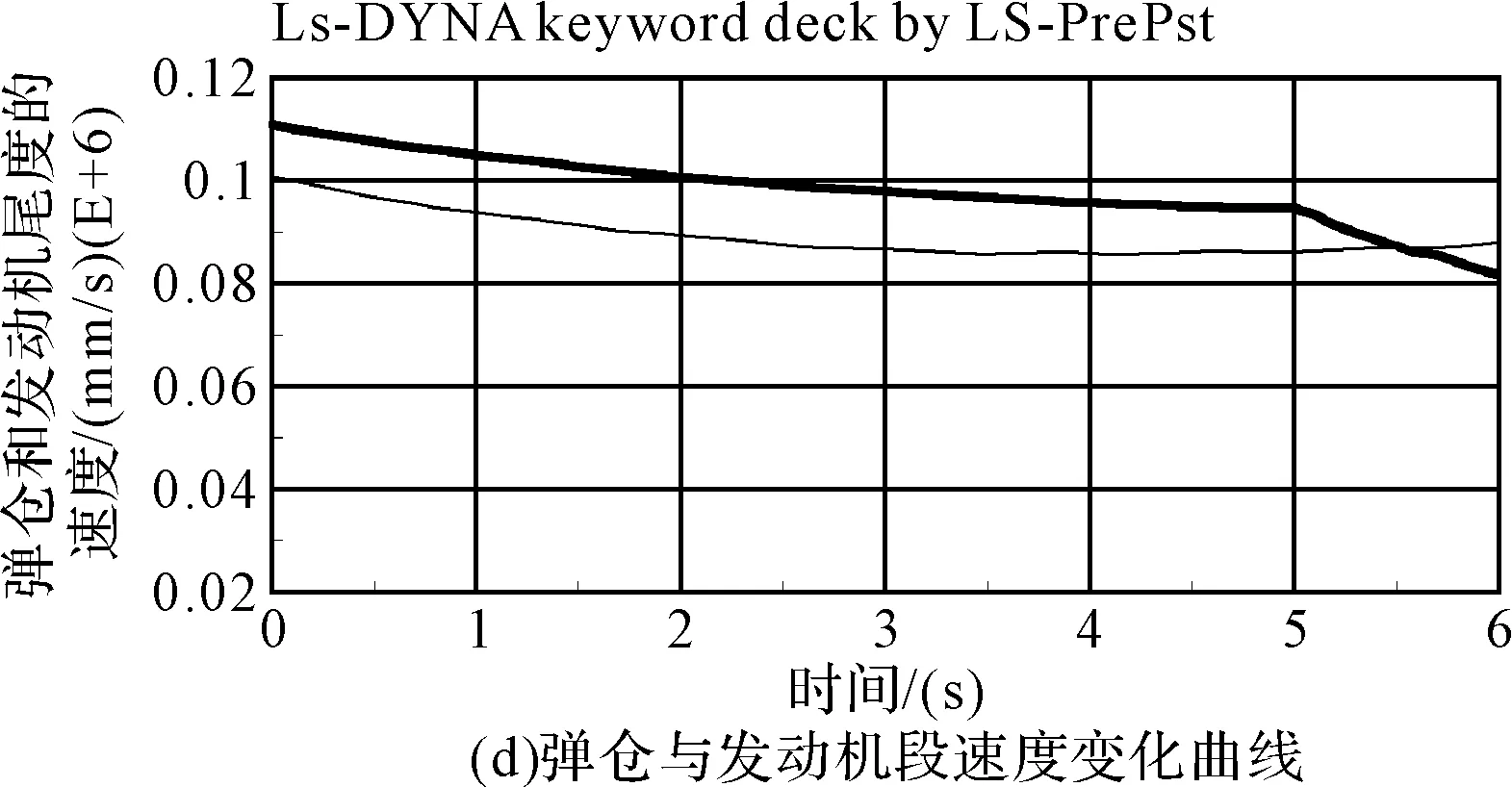
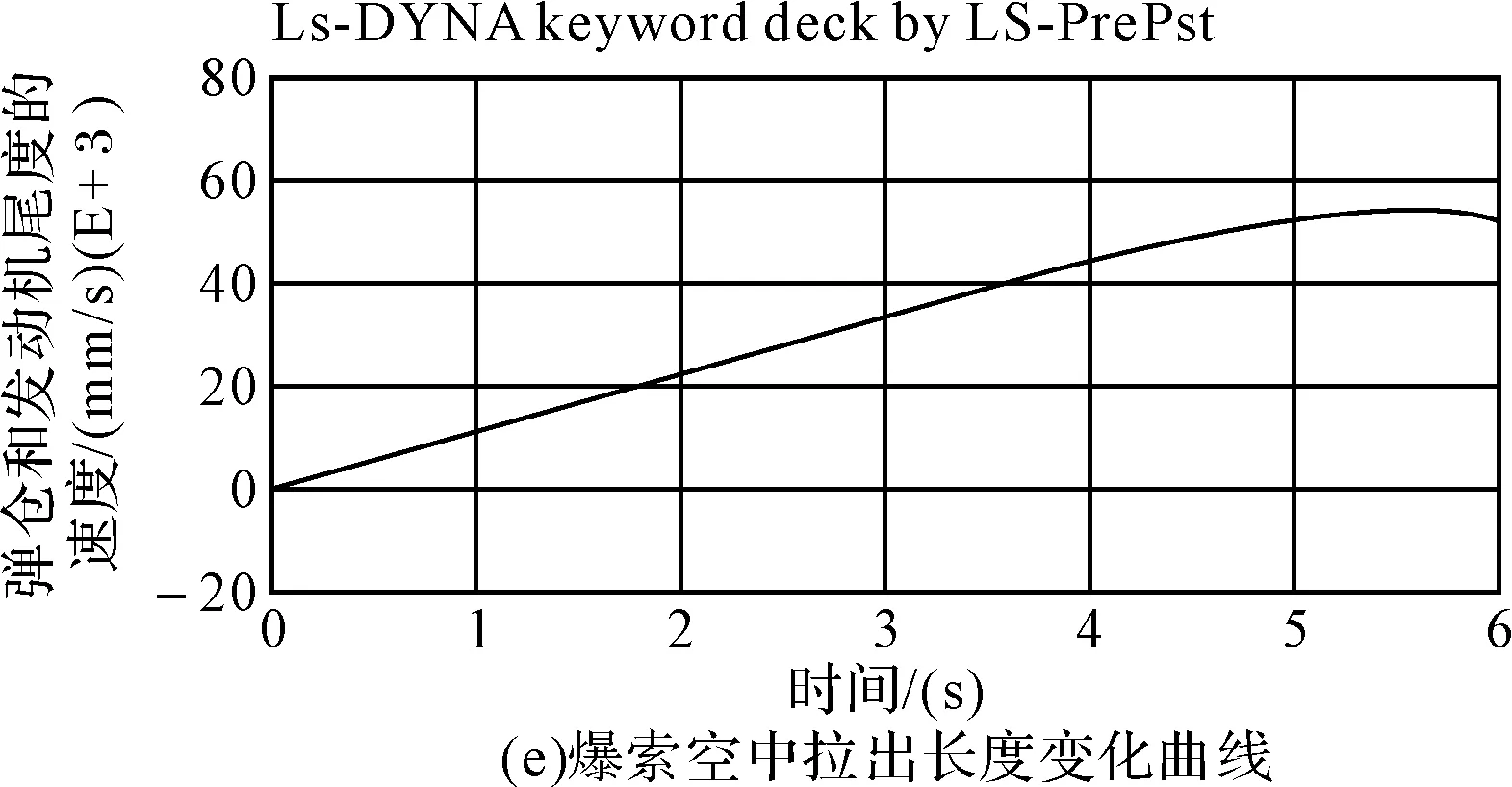
图6 爆索空中弹道分析图
由图6(a)、(b)可以看出,火箭弹燃气作动分离后,爆索在发动机段与弹仓之间相对分离速度以及发动机段本身气动阻力的作用下逐渐拉出、拉直并下落。图6(c)显示了弹仓、爆索子弹以及发动机段在各自气动力、重力以及连接绳拉力的作用下的运动轨迹,其中子弹的运动轨迹在不断波动。图6(d)为弹仓和发动机段的速度变化曲线,由该图可知,弹仓与发动机段燃气作动分离后存在初始速度差,随后逐渐减速,而发动机段由于依次拉出子弹,速度存在轻微波动,最后当爆索拉直之后,弹仓与发动机段速度耦合,在连接绳拉力的作用下,弹仓速度迅速减小,发动机段速度迅速增大。图6(e)显示了爆索拉出长度的变化。火箭弹分离后,爆索从弹仓内迅速拉出,在弹仓与发动机段速度耦合时,爆索拉出长度达到最大,随后则开始减小。
5结语
本文在应用火箭弹外弹道理论,确定爆索拉出前初始弹道参数的基础上,通过应用LS-DYAN软件建立了有限元模型,仿真分析了爆索空中弹道,得到如下三点结论:
1) 本文所设想的爆破火箭弹利用燃气作动分离,实现爆索拉出展开并呈“一”字形落地理论上可以实现。
2) 应用LS-DYAN有限元软件平台进行爆索空中弹道的仿真研究较为直观、精确,为此类弹道轨迹的建模分析提供了新的基于有限元平台的思路。
3) 要想实现爆索在全长拉直的瞬间同时落地起爆,达到最大的爆破长度,则需要进一步分析不同分离点、不同相对分离速度对爆索空中拉直长度的影响。
参 考 文 献
[1] 徐明有.火箭外弹道学[M].哈尔滨:哈尔滨工业大学出版社,2004:95-105.
[2] 周曾素,黄惠冲.弹道学[M].武汉:海军工程大学出版社,1996:121-130.
[3] 马利兵,林都.基于MATLAB的外弹道模型仿真研究[J].中北大学学报,2006,27(5):412-415.
[4] 吴志强,张晏铭,秦浩东.龙格—库塔方法与差分法的比较[J].成都大学学报,2014,33(4):337-338.
[5] 陈国光,田晓丽,赵捍东,等.二维弹道修正火箭弹弹道方案研究[J].弹箭与制导学报,2002,22(4):161-163.
[6] 王少飞.基于固定舵的火箭弹二维弹道修正控制方法[D].北京:北京理工大学,2015.
[7] 陈雄.整体式固体火箭冲压发动机内外弹道一体化计算[D].南京:南京理工大学,2014.
[8] 高滨.火工驱动分离装置的应用[J].航天返回与遥感,2004,25(1):55-59.
[9] 赵海鸥.LS-DYNA动力分析指南[M].北京:兵器工业出版社,2003:58-74.
[10] 白金泽.LS-DYNA3D理论基础与实例分析[M].北京:科学出版社,2005:30-59.
[11] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual[G]. Version 971,2007.
中图分类号TJ012.3
DOI:10.3969/j.issn.1672-9730.2016.03.021
作者简介:万业廷,男,硕士研究生,研究方向:弹箭外弹道学。
收稿日期:2015年9月4日,修回日期:2015年10月25日
