基于变形监测的金龙沟料场边坡失稳时间预测

冷超勤，张 扬（雅砻江流域水电开发有限公司，四川成都 610000）



基于变形监测的金龙沟料场边坡失稳时间预测

冷超勤，张 扬
（雅砻江流域水电开发有限公司，四川成都 610000）

摘 要：在加强现场检查的同时，高度重视安全监测及资料的深入分析，科学构建边坡失稳预测预报与稳定性评价模型和方法，对及时发现边坡工程安全隐患，实时调整施工过程，确保边坡工程安全具有极其重要的意义，亦是边坡工程领域长期关注的研究课题。基于此，本文以金龙沟料场边坡为依托，开展了相关预测模型、预报方法的研究，进行了金龙沟料场边坡失稳垮塌案例分析，证实了双曲线预测模型、非等时距GM（1，1）模型、黄金分割法、变形速率判据法的可行性、有效性。

关键词：金龙沟料场边坡；安全监测；现场检查；失稳预测预报

0 前 言

水利、交通和建筑等工程会形成大量的大坝坝肩边坡、料场边坡、铁路和公路的道路边坡。边坡的稳定问题不仅关系到工程本身的安全，同时也涉及到整体环境的安全。边坡的失稳破坏不仅会直接影响工程建设本身，而且也会通过环境灾难对人民生命财产安全带来影响和灾害。深入分析和掌握边坡变形规律，科学预测预报边坡失稳破坏，对防灾减灾具有十分重要的意义。

金龙沟料场为桐子林水电站工程的主要料场，该料场边坡在2010年10月23日发生垮塌，由于高度重视监测资料的及时分析，借此建立了预测模型，并结合现场巡查情况，临滑前成功预测了边坡失稳时间，并及时预警，提前撤离施工人员、设备，才避免了人员伤亡和重大经济损失。该案例充分说明了边坡安全监测及其科学分析对于边坡工程的重要性。以该料场边坡垮塌案例为依托，基于该工程宝贵的监测资料，开展边坡失稳预测预报模型、方法研究，不仅具有重要的科学意义，对其他边坡工程亦具有重要的参考价值。

1 工程概况

1．1 概 述

桐子林水电站位于四川省攀枝花市盐边县境内，系雅砻江下游最末一个梯级电站。金龙沟料场为原二滩电站人工骨料场开采剩余部分（见图1），现为桐子林水电站工程的主要料场，位于二滩电站左岸坝肩上游金龙沟谷坡左侧，距二滩大坝直线距离约700 m，距桐子林电站19 km。料场右侧紧邻金龙山滑坡。分布高程1 330～1 600 m，料场区总面积约0．1 km2，地质储量约670万m3（以开采至高程1 300 m计）。

图1 二滩水电站原料场边坡

2009年11月料场边坡在原料场的基础上开始揭顶开挖，2010年9月底开挖至高程1 560．00～1 594．00 m，边坡揭顶开挖工作基本结束。金龙沟料场揭顶边坡于2010年10月23日下午5 h 33 min出现垮塌，垮塌桩号约为0－30．00～0＋90．00 m，顺坡长约120 m；垮塌高程约为1 562．00～1 685．00 m，最大垮塌高度约为120 m，垮塌面积近1万m2，垮塌厚度约15～25 m，垮塌方量估计约20万m3。由于预警及时，施工人员疏散得力，垮塌未造成任何人员伤亡及设备材料损失。垮塌前后照片如图2、3所示。

图2 金龙沟料场边坡垮塌前现场

图3 金龙沟料场边坡垮塌后现场

1．2 金龙沟料场边坡安全监测概况

根据桐子林金龙沟料场边坡的地质情况及结构支护措施，采用外部变形观测墩、多点位移计、测斜孔、锚杆应力计、锚索应力计等仪器设备，对边坡表面及深部变形和锚杆、锚索支护应力情况进行监测。保障开挖过程安全为主要设计目的，采用仪器监测和人工巡视检查相结合的观测方法。综合考虑料场边坡的破坏机理、稳定条件、整体稳定性和局部稳定性，在金龙沟料场边坡1 611 m以上高程共设AA、B－B和C－C三个监测剖面，在1 611 m以下高程共布设LCBP1、LCBP2、LCBP3、LCBP4和LCBP5五个监测剖面。

截至2010年10月23日，金龙沟料场边坡完成1 611 m以上高程3个监测断面的多点位移计、锚索测力计的埋设。监测布置见图4～6。

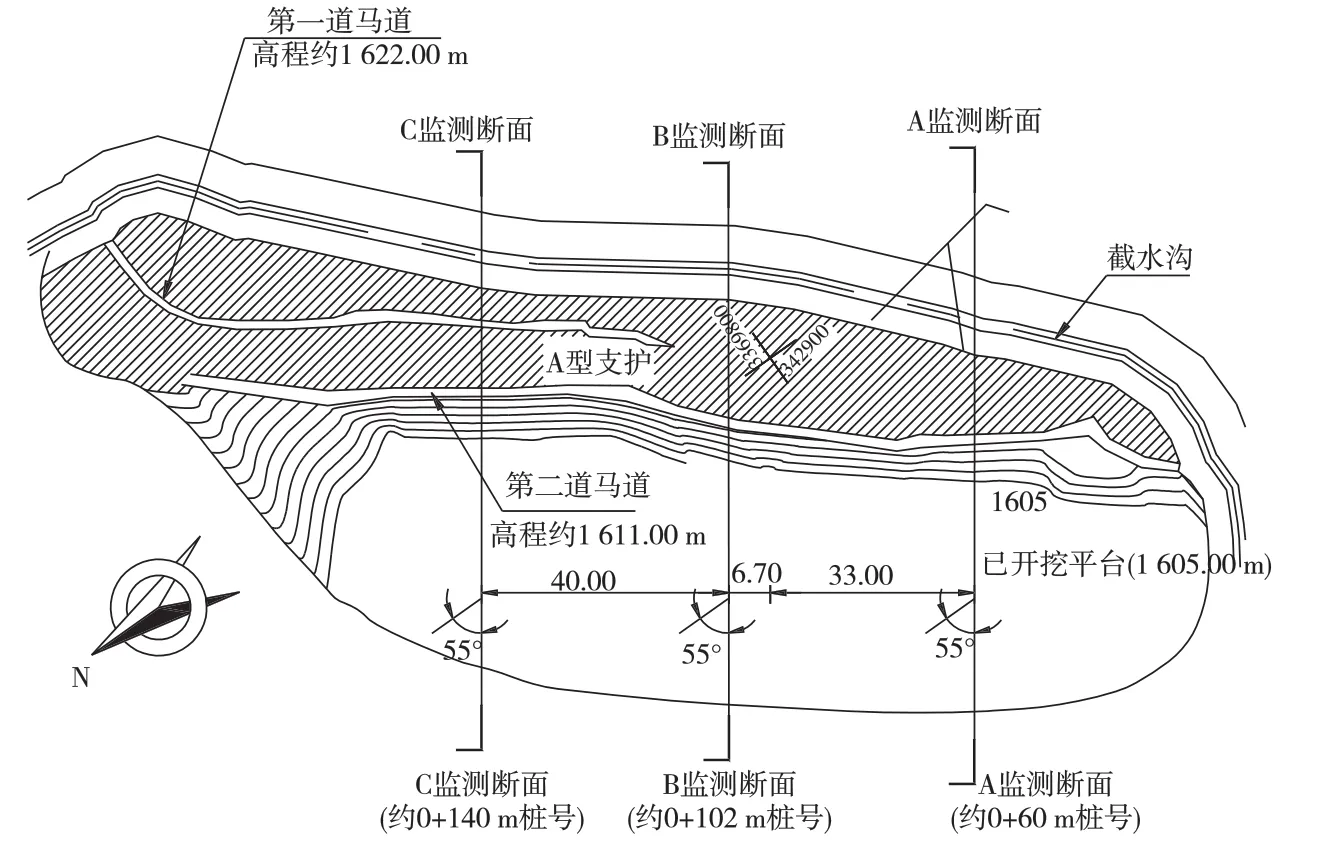
图4 1 611 m高程以上边坡监测剖面布置示意

2 基于变形监测数据的边坡失稳预测预报方法

边坡变形是边坡稳定状况最直观的反映，合理分析、预测边坡变形规律及其与边坡稳定关系，对边坡失稳的可靠预报具有重要意义。由于工程及地质条件的复杂性，在分析边坡变形监测资料并预测其变化规律时，常常会出现拟合不佳的现象，进而会影响到对边坡性状及规律的分析和预测。因此针对边坡特点探讨合适的分析预测模型及边坡失稳时间的预报方法具有重要的意义。

图5 A－A剖面监测仪器布设示意

图6 B－B剖面监测仪器布设示意

2．1 边坡变形预测模型

2．1．1 双曲线预测模型

双曲线法认为边坡变形量与时间近似呈双曲线函数关系［1］。这是一种纯经验的曲线配合方法，利用实测位移—时间曲线确定拐点t0（起点，通常取恒载下的某个时刻），将实测S（t）—t曲线的起点放在t0处，则位移时间曲线将接近于双曲线，可近似用双曲线表示，即：

式中 S（t）——为t时刻的位移值；

t0——为拐点处的时间或时间零点；

S0——为对应t0时刻的位移值；

a、b——为曲线方程待拟合的参数。

2．1．2 灰色预测模型

边坡的变形破坏是受内外多因素综合作用的结果，由于边坡变形破坏机理的复杂性和人们认识的局限性，仍存在许多因素、参数及其相关性不十分清楚，可以认为边坡变形系统是个灰色系统。自1988年陈明东等首次将灰色系统理论中的GM（1，1）模型应用于滑坡变形预测以来，该模型及其改进的非等时距GM（1，1）模型被广泛应用于滑坡变形预测中［2］。

非等时距GM（1，1）模型反应了一个变量对时间的一阶动态微分函数，可以确定观测值与变化的关系，对未来的观测量变化进行预测。其相应的微分方程为

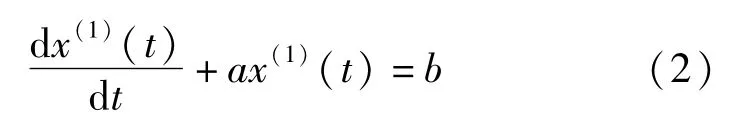
式中 x（1）——为经过一次累加生成的数列；

t——为时间；

a——为发展系数；

b——为灰色作用量。

设原始数列X（0）＝（x（0）（1），x（0）（2），x（0）（3），…，x（0）（n）），对X（0）进行一阶累加可生成新的序列X（1）＝（x（1）（1），x（1）（2），x（1）（3），…，x（1）（n）），其中，建立灰色非等时距GM（1， 1）模型，得到如式（2）所示关于x（t）的灰色一阶微分方程。对微分方程进行离散化，可得到如下近似线性方程：

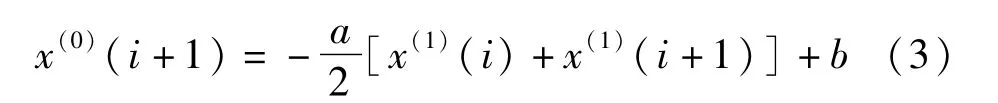
式中：i＝0，1，2，…，n；a、b为待定系数，可用最小二乘法求得。令

则

式中：YN为原始数列矩阵，用YN＝｛x（0）（2），x（0）（3），…，x（0）（n）｝T求得；参数β由最小二乘法原理可得到，其估值＾β＝（BTB）－1BTYN。

在考虑初始条件x（1）（1）＝x（0）（1）时，白化微分方程的解为：

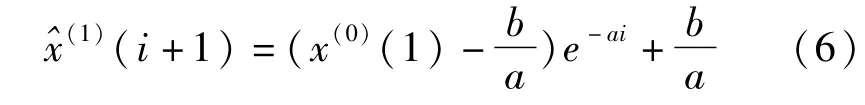
通过累减还原，可求出原始序列：

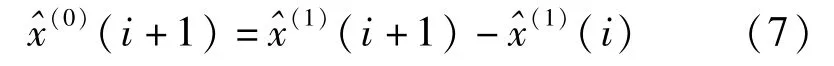
非等时距GM（1，1）模型算法流程如图7所示。

2．2 基于变形状况的边坡失稳时间预测方法

2．2．1 黄金分割法

张倬元教授通过收集分析若干岩体失稳实例的位移观测曲线发现，岩体失稳前整个变形可分为线性稳定变形及非线性非稳定破裂发展两个阶段，这两个阶段的历时T1、T2符合“黄金分割”原理［3］，即有：

由岩体系统状态的历时曲线，获知岩体的变形发展进入了非线性的累进性破坏阶段后，即可得知其线性稳态变形的历时T1，由式（8）则可求得将要经历的非线性阶段历时T2，从而得出岩体失稳破坏的时间。

图7 灰色非等时距GM（1，1）模型算法流程

2．2．2 变形速率判据法

滑坡的发生，本质上属斜坡上的物质以一定的速度沿某滑移面向下移动所致。因此，以斜坡体上物质变形速率的大小来作为滑坡是否会发生、何时发生的预报判据更直观、更可靠。目前，人们都直接或间接地使用滑坡变形速率作为判据来对滑坡作出临滑预报。

李秀珍研究大量滑坡工程实例，通过对现有一些滑坡的统计结果表明，一般黏土斜坡的临界变形速率为0．1 mm／d；岩质边坡一般为10 mm／d、14．4 mm／d或24 mm／d［4］。

3 基于监测资料的金龙沟料场边坡失稳分析

3．1 巡视检查情况分析

2010年9月29日巡视发现，在1 611．00 m高程马道（桩号K0＋090．00 m附近）出现裂缝，其最大宽度约3 mm；在1 562．00 m高程新发现一缓倾坡外泥化夹层，长约30 m，厚约3～10 cm，其上层已相对下层滑动约30 mm。2010年10月21日巡视发现，桩号0＋00．00～0＋90．00 m段边坡，坡体前缘出现一系列竖向裂缝；桩号0＋00．00 m开口线附近，分别于高程1 590．00 m、1 600．00 m、1 620．00 m处出现顺坡向裂缝；桩号0＋90．00 m处裂缝变宽，最大宽度约30 mm，竖向裂缝于高程1 617．00 m、1 623．00 m两处将锚礅与锚索梁连接处错开；桩号0＋65．00～0＋85．00 m，高程1 062．00～1 088．00 m，顺裂隙（N70°E SE∠50°）出现断续挤压裂缝，长约16 m，宽3～10 mm。

经现场巡查及分析推测桩号0＋00．00～0＋90．00 m段边坡，存在整体垮塌的可能。

结合巡视检查情况分析和监测资料分析可得A－A典型剖面在滑动范围内，的测值数据可作为关键依据预测失稳时间。

边坡实际失稳的时间是2010年10月23日17：33。黄金分割法、变形速率判据法的预测结果都与之接近。对比上述模型可知：

（1）黄金分割法十分简便，而且适用范围广，不论岩体的地质条件、经历的变形时间长短，皆可利用此法预测失稳时间；且不需要过多观测数据。黄金分割法的难点在于准确确定边坡变形的线性阶段T1，本案例位移—时间曲线为光滑型曲线，且拐点较明显，很适合用该法。但如果位移－时间曲线为振荡型、波动型，确定边坡变形的线性阶段T1将会有难度。

（2）双曲线预测模型适用于中长期预测，对于边坡线性变形阶段到非线性变形阶段的变形数据拟合精度高，预测效果好；非等时距GM（1，1）模型只适用于临滑前短期预测，对于非线性阶段的变形数据拟合精度较高，而对于线性变形阶段到非线性变形阶段的变形数据拟合精度较低。

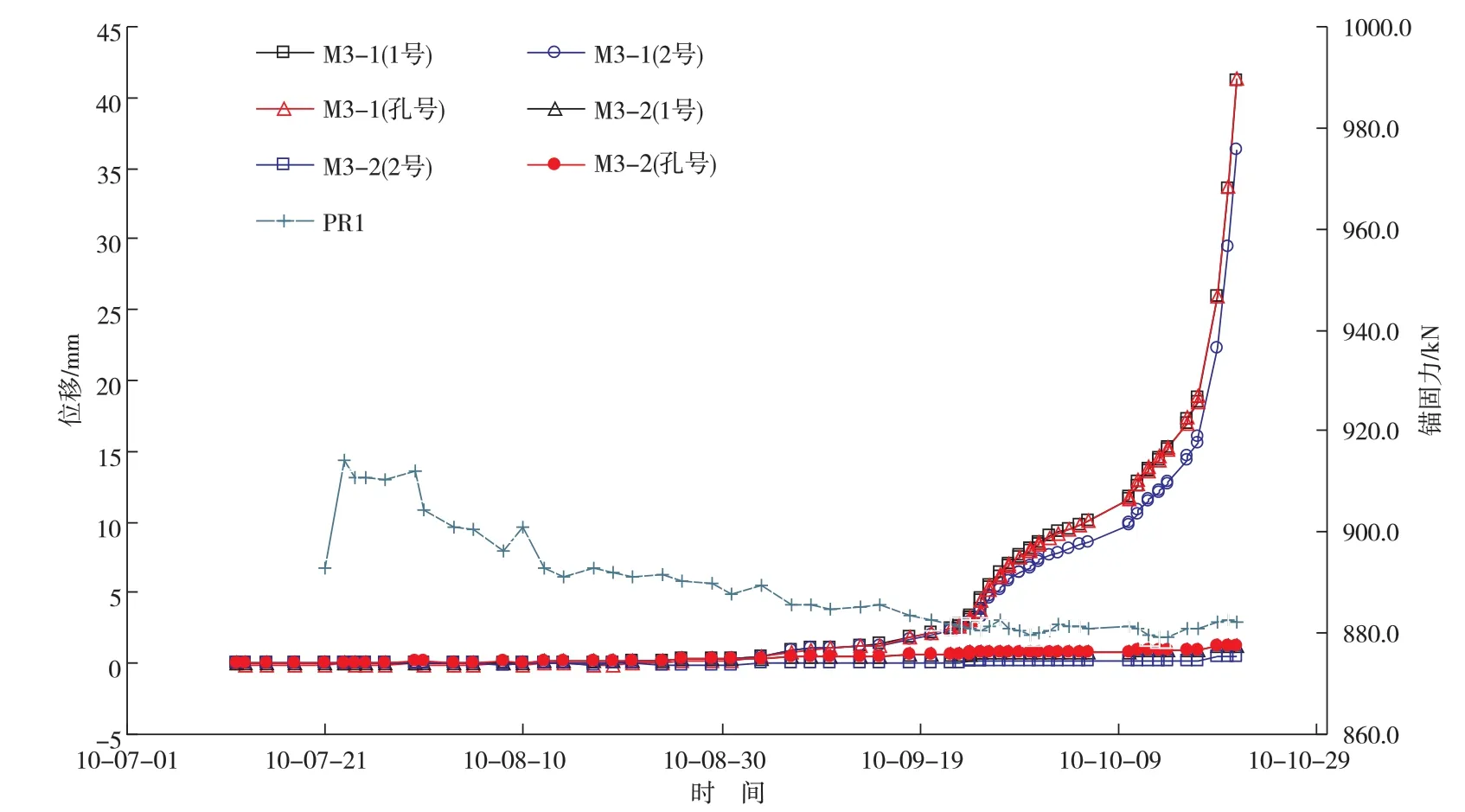
图8 A－A监测剖面多点位移计和锚索测力计测值－时间过程线

表1 各预测方法预测时间汇总

（3）该工程案例再次验证了位移变形速率判据对于滑坡预测的实用性，地质条件类似的岩质边坡可取变形速率10 mm／d作为判据对滑坡作出临滑预报。

4 结 论

本文以金龙沟料场边坡为依托，以该料场边坡垮塌案例分析为目标，充分依据该边坡监测资料和现场检查成果，开展边坡失稳预测预报方法研究。主要研究内容及相关结论如下：

（1）研究基于监测资料的边坡变形预测模型和边坡失稳时间预测方法。论述了边坡变形双曲线预测模型、非等间距GM（1，1）模型的建模原理和过程，分析阐述了利用边坡变形实测数据序列和预测成果，实现边坡失稳时间预报的黄金分割法、变形速率判据法。

（2）针对金龙沟料场边坡失稳垮塌案例，在对该次事故前巡查资料和监测资料详细分析的基础上，基于该边坡变形实测数据和上述模型计算值，应用文中所述边坡失稳时间预报方法，进行了该边坡失稳时间的分析预报，得出了与实际情况较吻合的预报结果。证实了双曲线预测模型、非等时距GM （1，1）模型、黄金分割法、变形速率判据法的可行性、有效性。

（3）分析阐述了各种预测方法的优缺点及其适用条件，便于该类方法的推广。

参考文献：

［1］ 汪国斌，李融融，董泽荣．边坡稳定预测方法在桐子林水电站边坡垮塌的应用［J］．云南水利发电，2012，23（3）：23－25．

［2］ 陈明东，王兰生．边坡变形破坏的灰色预报方法［C］／／全国第三次工程地质大会论文选集（下）．成都：成都科技大学出版社，1988：1226－1240．

［3］ 张倬元，黄润秋．岩体失稳前系统的线性和非线性状态及破坏时间预报的“黄金分割法”［C］／／全国第三次工程地质大会论文选集（下）．成都：成都科技大学出社，1988：1233－1240．

［4］ 李秀珍，许强，黄润秋，汤明高．滑坡预报判据研究［J］．中国地质灾害与防治学报，2003，18（4）：8－14．

作者简介：冷超勤（1987－），男，湖北武汉人，助理工程师，从事项目工程管理工作。

收稿日期：2015-10-13

中图分类号：TU457

文献标志码：B

文章编号：1003－9805（2016）01－0084－05