EMD－SVD及粒子群优化的SVM变压器局部放电模式识别

董朋，张建文，贾立敬

(1.国华徐州发电有限公司，江苏徐州221000;2.中国矿业大学，江苏徐州221166)

EMD－SVD及粒子群优化的SVM变压器局部放电模式识别

董朋1，张建文2，贾立敬2

(1.国华徐州发电有限公司，江苏徐州221000;2.中国矿业大学，江苏徐州221166)

为了对变压器的局部放电信号进行特征量提取以及模式识别，在分析EMD和SVD理论的基础上，提出了EMD－SVD和PSO－SVM相结合的方法。将选取的四种去噪后的局部放电信号(空气中电晕、沿面、气隙，油中气隙)经EMD分解为由高到低的固有模态函数，再利用SVD对其进行数据压缩，提取出14个反应PD信号本质的特征量，并将其输入到经粒子群优化的支持向量机进行模式识别。仿真结果表明，此方法能够较好地识别出四种局部放电信号，与未经优化的SVM、GA－SVM、GRID－SVM相比，经粒子群优化的支持向量机分类准确率较高、速度较快。

EMD;SVD;PD;粒子群

1 引言

随着现代社会工业化程度的不断提高，电力系统朝着超高压、大电网、大容量、自动化方向发展。大型电力变压器作为电力系统的主要设备，其造价昂贵、结构复杂，承担着联系不同电压等级电网的重任，其运行状态直接影响系统的安全水平和可靠性［1］。局部放电(PD)是电力变压器绝缘劣化的主要原因和早期表现形式，PD信号模式识别对大型电力变压器故障诊断和实时状态评估具有重要意义。

局部放电模式识别过程由特征量提取和分类识别组成。目前，国内外研究局部放电特征量提取的方法主要包括统计特征参数、威布尔参数［2］、分型特征参数［3］、矩特征参数［4－5］等。目前常用的分类识别方法有模糊聚类法［6］、人工神经网络法［7］、隐马尔科夫分类法［8］、支持向量机法［9］等。上述方法大多数针对大样本数据，鉴于经EMD－SVD提取出的局部放电信号特征量较少，因此选用专门解决具有非线性、样本少及维数高等特性的支持向量机方法(SVM)。支持向量机中参数选择影响其分类效果，粒子群算法是基于群体的具有全局寻优能力的优化算法，采用粒子群算法对高斯径向基核函数进行优化，搜索到最优(c，σ)，再将得到的参数进行验证，获得最优的支持向量机模型，提高了分类准确率。

本文采用EMD方法将4种去噪后的局放信号(空气中气隙、沿面、电晕，油中气隙)分别分解为由高到低的固有模态函数，通过SVD方法对其进行正交变换获得14个奇异值，将其输入到经粒子群优化的支持向量机，输出为4种局部放电故障。仿真发现其最终的分类结果与未经优化的SVM、GA－SVM、GRIDSVM相比，其识别精度和运算速度得到了大大提高。

2 基于EMD－SVD的PD信号特征量的提取

2.1 经验模态分解(EMD)理论

在信号分析中，经常遇到多时间尺度的非平稳、非线性信号。1998年，美国华裔科学家NordenE.Huang等人提出希尔伯特－黄变换(即HHT变换)，HHT变换由EMD分解和Hilbert变换两部分组成。EMD分解完全自适应的将多时间尺度复杂信号分解为由高到低的多个单一时间尺度的IMF信号。从而表现出良好的非线性、非平稳信号的局部分析能力。黄对IMF做出如下限定［10］:

(1)在给定的整个数据序列区间内，其极值点个数和过零点的个数相等，或至多相差一个。

(2)对任意时刻，由极大值拟合出的包络线和由极小值拟合出的包络线的均值为零，即信号关于零均值局部对称。其分解流程图如图1所示。

其具体的分解过程如下:

步骤1:找出信号的所有极值点，利用曲线拟合方法分别将所有极大值点和极小值点连接拟合成上、下两条包络线(本文采用3次样条插值函数拟合)，两条包络线的均值为m1，h1为信号与m1之差，即:

步骤2:判断h1是否满足IMF所限定的两个条件，若满足，则h1信号x(t)的第一个IMF分量，若不满足则令x(t)=h1，将x(t)代入式(1)，重复步骤1，循环k次(一般小于10次)，得到h1(k－1)－m1k=h1k，当h1k满足IMF两个条件时，则h1k为信号的第一个IMF分量，记为imf1。这种求取IMF分量的做法称为“筛分”。

步骤3:将imf1从信号x(t)中分离出来，得到的差值信号r1为:

图1 EMD分解流程图

步骤4:r1含有较多周期成分，对差值信号r1重复步骤1～3，得到x(t)的第二个IMF分量imf2，如此反复进行，直到imfn或残余分量rn满足终止条件时，EMD分解终止。

信号x(t)经分解后可表示为:

imfn代表信号频率从高到低的使瞬时频率能合理定义的IMF分量。对实测的去噪后空气中电晕放电信号进行EMD分解如图2所示，图中x(t)为原始的空气中电晕放电信号，imf1－imf14为固有模态函数，r(t)为残差。

2.2 奇异值分解(SVD)理论

奇异值分解理论的提出和完善经历了一个多世纪，其中具有代表性性的人物有Beltrami、Jordan、Autonne、Eckart和Yonng［11－13］奇异值分解的本质是正交变换，是谱分析理论在任意矩阵的推广。奇异值个数代表原矩阵中独立行(列)的个数，其值的大小反映各独立成分的构成。

在信号处理方面主要体现为数据降维、压缩、弱信号特征提取和分离等，实际意义为反映信号能量集中和信息包含情况，奇异值越大，说明其所对应的子矩阵所表达的独立成分在整个矩阵中越突出以及包含信息越多。奇异值分解反映矩阵的固有特征，得到的子矩阵相互正交，所以具有良好的平稳性，能最大限度的减少特征量的冗余，很适合对PD这种随机性信号的特征量提取［14］。

图2 空气中电晕放电信号进行EMD分解

2.3 局部放电信号特征量的提取

EMD－SVD就是利用EMD分解得到的各阶IMF分量构建矩阵进行奇异值分解，并将分解后的奇异值向量作为特征量。提取方法步骤如下:(1)根据EMD分解方法，对PD信号进行分解，利用经过去噪后的各个imfs形成固有模态矩阵。(2)对矩阵进行SVD，得到奇异值向量。表1为4种PD信号(空气中电晕、沿面、气隙，油中气隙)用EMD－SVD特征量提取方法得到的奇异值向量。PD信号长度为一个工频周期，用EMD分解得到的多个IMF分量组成奇异值分解矩阵，奇异值分解得到14个奇异值作为特征向量。表中每种PD类型取一个样本，A为空气中电晕放电、B为空气中沿面放电、C为空气中气隙放电、D为油中气隙放电。

表1 奇异值分解值

3 粒子群优化支持向量机的局部放电信号识别

支持向量机SVM是在统计学习理论的基础上提出的一种模式识别新方法，它是建立在统计学习理论和结构风险最小化原理基础上的学习机器［15］。特别是在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势。支持向量机在处理非线性问题时，将训练数据从原始模式空间经过特定核函数的非线性变换，映射到高维特征空间，变成线性可分问题，通过建立一个超平面，正反样本数据被分开，同时之间的距离最大化［16］。因此，SVM在处理非线性情况时，仅比线性情况多了一个非线性映射环节，假定该非线性映射为x→ψ(x)，则优化问题的对偶形式为:

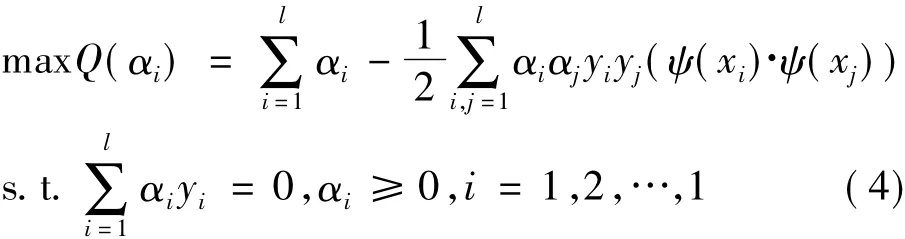
但是，原始空间中的数据点经过非线性变换后，被映射到非常高维的特征空间。在满足Mercer条件下为降低计算量，通过使用核函数K(xi，xj)=ψ(xi)· ψ(xj)来代替最优分类超平面的点积，从而避免高维进行复杂的运算。因此，式(4)变为:

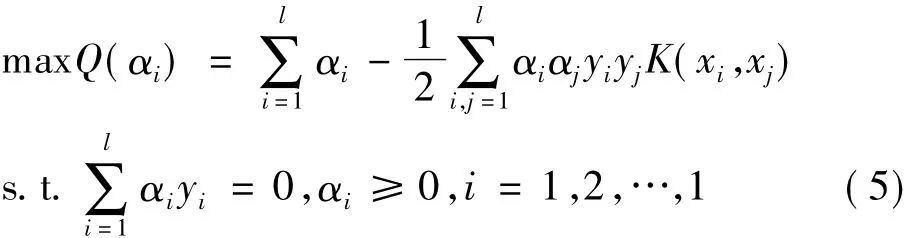
而非线性SVM的分类函数为:

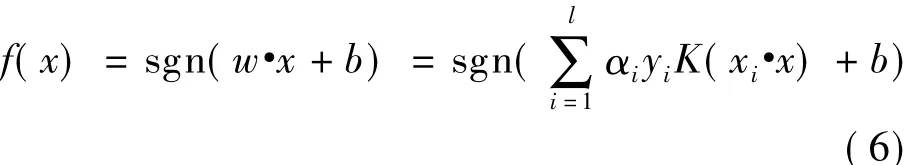
采用不同的内积核函数将形成不同的SVM算法，综合支持向量个数、对阶次的影响程度，考虑选择径向基核函数作为支持向量机的核函数。同时通过调节参数σ可以改变分类准确率，本文采用粒子群算法对其参数进行优化。

3.2 基于粒子群算法的SVM参数寻优

3.2.1 粒子群算法

粒子群算法用速度、位置以及适应度值表征粒子特征，首先在可行解空间中初始化粒子速度和位置，通过适应度函数计算其适应度值，根据适应度值对个体极值和群体极值进行更新，再利用个体极值和群体极值更新粒子位置和速度，即

为此，笔者认为在“二考”复习过程中要调动学生的主观能动性，突出学生的主体地位，避免教辅材料的结构和教师的思路“绑架”学生，忽略学生自己的构建和思考。本文通过对比常规复习和基于项目学习理论的复习之间的差异，提出项目学习理论在新高考生物“二考”复习中的应用方法。

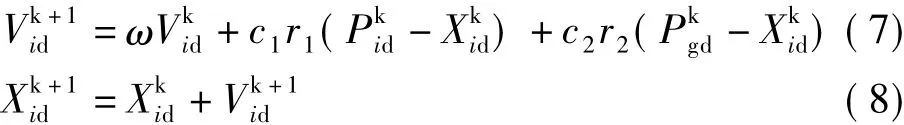
其中，Pi=(Pi1，Pi2，…，PiD)T为个体极值，Pg= (Pg1，Pg2，…，PgD)T为种群的群体极值，ω为惯性权重，d=1，2，…，D;i=1，2，…，n;k为当前迭代次数;Vid为粒子速度，Xid为粒子位置;c1和c2是非负的常数，成为加速因子;r1和r2是分布于［0，1］区间的随机数。判断迭代次数是否达到了所设置的最大迭代次数或者是否搜寻到了小于设定的误差，若满足则终止，否则继续循环迭代。其流程图如图3所示。

图3 粒子群算法流程图

3.2.2 基于粒子群算法的SVM参数寻优

粒子群算法采用k——折交叉验证法计算的平均准确率αk－cv作为适应度函数，对支持向量机分类器的核函数参数σ(径向基函数的宽度)和惩罚参数c寻优，提高了支持向量机的分类精度和实用性能。基于粒子群算法的支持向量机参数寻优步骤如下:

步骤1:初始化粒子群，确定支持向量机参数寻优终止条件、种群规模，设定迭代次数T、权重因子ω;

步骤3:按照式(7)和式(8)进行计算，对粒子的位置和速度进行更新;

步骤4:判断是否满足终止条件，若满足则将输出的(c，σ)赋给SVM进行训练，否则继续循环迭代;

步骤5:用训练好的支持向量机进行预测，对测试集的实际值与预测值进行比较分析，判断分类的准确程度。

4 实例仿真与结果分析

4.1 实例仿真

为了验证该方法的可行性，本文在MATLAB平台上进行仿真，将经EMD－SVD变换后的去噪信号作为样本数据进行仿真，首先将样本数据分为训练集和测试集，并对其进行预处理，通过粒子群算法寻找最优的参数(c，σ)，利用最优参数对SVM进行训练，再对测试集进行预测，其完整模型如图4所示。

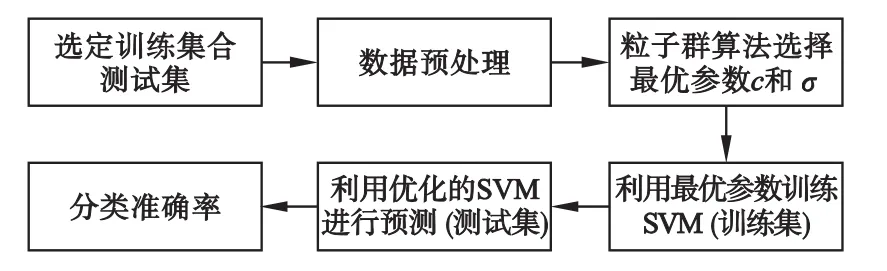
图4 基于PSO－SVM的模型

选取四种典型的经EMD－SVD分解后的局部放电信号(空气中电晕、沿面、气隙，油中气隙)作为样本，分为训练集和测试集，其对应的样本如表2所示。

表2 训练集和测试集对应的样本分布

初始化粒子群，设定迭代次数为100，种群数量为56，SVM惩罚参数C和RBF核参数σ的范围为［2－15，215］和［2－10，210］，惯性权重ω的范围为［0.4，0.9］，c1=c2=2，经过优化选择后最终得到支持向量机最优惩罚参数C=2.2965、σ=34.7128，最佳分类准确率为90.0%。最佳适应度曲线如图5所示。

图5 最佳适应度曲线

4.2 结果分析

将寻优得到的(c，σ)进行验证，其结果为Accuracy=90.0%(18/20)(classification)。

为了验证经PSO优化的SVM方法的有效性，分别对未经优化的SVM、经GRID优化的SVM、经GA优化的SVM、经PSO优化的SVM与经PSO优化的SVM进行对比分析。比较结果如表3所示。

表3 不同方法对局部放电信号识别的比较

由表3发现，经过优化的SVM比未经优化的SVM准确率得到不同程度的提高，但对于网格法进行优化时所需时间较长;遗传算法优化的支持向量机准确率虽然得到了很大程度地提高，但是遗传算法进行优化时比粒子群优化训练所需时间要长;而采用粒子群算法相对于遗传算法，不需要编码，没有交叉、变异操作，粒子只是通过内部进行更新，原理更简单、参数更少、实现更容易，并且其识别准确率最高，训练和测试时间最短，因此选用粒子群优化的支持向量机对变压器局部放电信号进行模式识别。

5 总结

本文提出一种基于EMD－SVD方法对去噪后的4种PD信号进行特征量提取，经过奇异值分解得到14个特征值;采用粒子群算法对SVM的参数进行优化，获得最优的支持向量机模型;将特征量输入到经过优化的支持向量机，对变压器局部放电信号进行模式识别。仿真结果表明，与未经优化的SVM、GA－SVM、GRID－SVM相比，经过粒子群优化的支持向量机分类时间最短、识别精度最高。

［1］朱永利，尹金良.组合核相关向量机在电力变压器故障诊断中的应用研究［J］.中国电机工程学报，2013(22):68－74.

［2］胡文堂，高胜友，余绍峰，等.统计参数在变压器局部放电模式识别中的应用［J］.高电压技术，2009，35(2):277－281.

［3］R Candela，G Mirelli，R Schifani.PD recognition by means of statistical and fractal parameters and aneural network［J］.IEEE Transations on Dielectrics and Electrical Insulation，2000，7(1):87－94.

［4］Gao Kai，Tan Ke-xiong，Li Fu-qi，Wu Cheng-qi.The Use of Moment Features of Partial Discharges in Generator Stator Winding Models［C］.Pro-ceedings of the 6th International Conference on Properties and Applications of Dielectric Materials，2000:290－293.

［5］张正晗.基于图像灰度矩特征的气体电晕放电WFCM辨识方法［J］.哈尔滨理工大学学报，2010，15(2):14－18.

［6］L.Hao and P.L.Lewin.partial discharge source discrimination using a support vector machine［J］.IEEE Transationson Dielectrics and Electrical Insulation，2010，17(1):189－197.

［7］王重云.基于神经网络的变压器故障诊断技术研究［D］.大庆:东北石油大学，2013.

［8］何洪军.变压器故障诊断识别理论与方法的研究［D］.上海:上海交通大学，2011.

［9］肖燕彩.支持向量机在变压器状态评估中的应用研究［D］.北京:北京交通大学，2008.

［10］N.E.Huang，Shen Z，S.R.Long，etal.The empirical moded ecomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.ProcRsoLond，1988，454:56－78.

［11］Aharon，Michal，Elad，et al.An algorithm for designing over complete dictionaries for sparse representation［J］.IEEE Transactions on signal Processing，2006，54(11):4311－4322.

［12］Vozalis M G，Margaritis K G.Using SVD and demographic data for the enhancement of generalized collaboratire filtering［J］.Information Sciences，2007，177(15):3017－3037.

［13］丛飞云.基于滑移向量序列奇异值分解的滚动轴承故障诊断研究［D］.上海:上海交通大学，2012.

［14］唐炬，李伟，欧阳有鹏.采用小波变换奇异值分解方法的局部放电模式识别［J］.高电压技术，2010，30(7):1686－1691.

［15］华丁剑.基于支持向量机的油浸式变压器故障诊断研究［D］.长沙:长沙理工大学，2012.

［16］He H，Starzyk J A.A self-organizing learning array system for power quality classification based on wavelet transform［J］.IEEE Trans on Power Delivery，2006，21(1):286－295.

张建文(1968.4－)，男，汉族，宁夏贺兰县人，教授，博士，研究方向:从事电气设备状态监测与故障诊断技术、高电压技术方向研究;

贾立敬(1986.7－)，女，汉族，河北省衡水市，硕士研究生，主要研究方向:主要从事电气设备状态监测与故障诊断技术方向研究工作。

The Pattern Recognition of Partial Discharge Based on EMD－SVD and PSO Optimizing Parameters of SVM

DONG Peng1，ZHANG Jian-wen2，JIA Li-jing2
(1.Guohua Power Generation of Xuzhou，Xuzhou 221116，China;2.China University of Mining and Technology，Xuzhou 221116，China)

In order to extract and distinguish the pattern for the partial discharge signals of transformer，after analyzing thoretical of EMD and SVD，the method of combining between EMD-SVD and PSO-SVM is proposed.The four selected denoising partial discharge signals(corona、surface、cavity in air，cavity in oil)decomposes into intrinsic mode functions from high to low through EMD，using its SVD realizes data compression，thereby extracting the feature quantity of fourteen reactive nature of the PD signal.At the same time，pattern discrimination by entering into the PSO optimizing parameters of SVM.The result show that，this method can identify the four kinds of partial discharge signals preferably，and compared with non-optimized SVM，GA-SVM，GRID-SVM，it has higher classification accuracy rate and faster by PSO optimizing parameters of SVM.

EMD;SVD;PD;PSO

TM411

A

1004－289X(2016)04－0016－06

2016－06－10

董朋(1982.10－)，男，汉族，江苏省徐州市，工程师，工程硕士研究生，研究方向:主要从事火力发电厂电气设备技术管理工作;