二阶双曲问题各向异性有限元的超收敛分析

马国锋

(许昌学院 数学与统计学院,河南 许昌 461000)

二阶双曲问题各向异性有限元的超收敛分析

马国锋

(许昌学院 数学与统计学院,河南 许昌 461000)

克服传统有限元要求剖分网格满足正则假设(或拟一致假设)的限制 ,利用具有各向异性特征的双线性元对二阶双曲问题进行研究，并借助于积分恒等式技巧和插值后处理技术, 得到了各向异性网格下的超逼近和超收敛分析.

各向异性网格;超逼近;超收敛

最近许多文章涉及各向异性剖分下的有限元方法分析，即研究基于摆脱剖分正则性的有限元方法，陈绍春教授提出一种验证适用于各向异性情况的有限元的分析方法，可用于一些Hermite元，拓宽了各向异性元的范围[1].各向异性情况下，插值定理可以应用于二维或三维情况的类Wilson元和改进的五节点矩形元.另一方面，有限元解的超收敛性研究对提高计算效率有重要意义.林群、严宁宁、周爱辉等考虑运用积分恒等式来处理许多单元得到超收敛性质[2].

本文是在各向异性网格下，充分利用单元的构造性质，给出用于二阶双曲问题的协调双线性元的超逼近与超收敛结果.都可得到与正则网格下相同的收敛阶.

1 二阶双曲问题及单元构造

考虑模型问题[2]

(1)

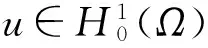
(2)

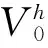
(3)

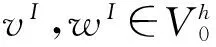
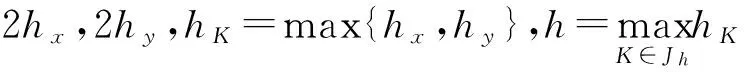
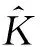
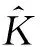
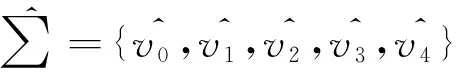
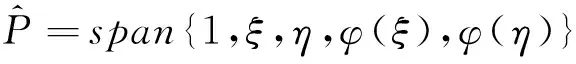
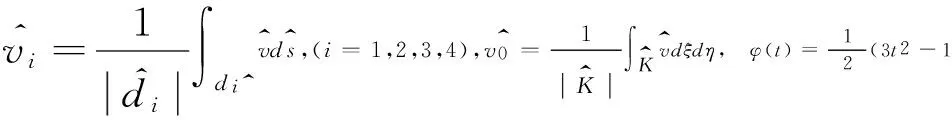
通过计算，可得插值为：

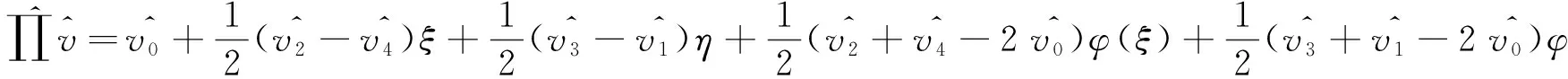
那么，我们有：

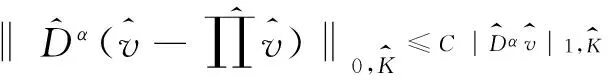
(4)

2 有限元逼近格式及超逼近分析

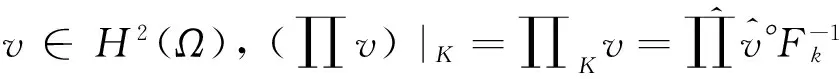
相应的有限元空间为：

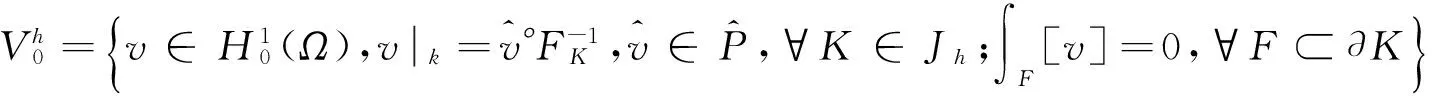
这里[v]表示v跨过单元边界的跳跃度，当F⊂∂Ω时，[v]=v.

为了研究上述问题的超逼近性质，首先给出下面两个重要引理：

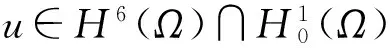
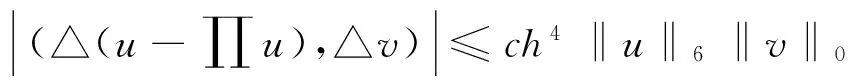
引理3[4]设ut∈H4(Ω),则

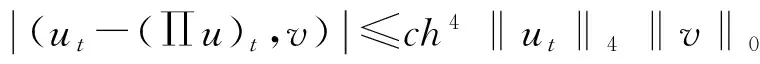
利用引理2和引理3我们可以得到下面重要的超逼近结果.

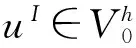
(5)

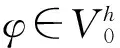
取φ=θt,由引理2、引理3及插值理论知

(6)

对(6)式积分并注意到θ(0)=θt(0)=0,

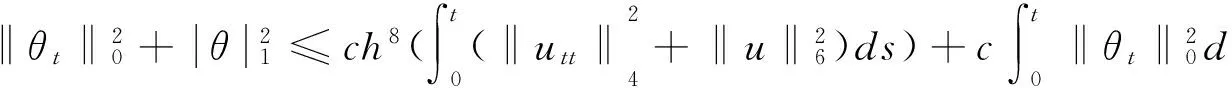
(7)

由Gronwall引理得

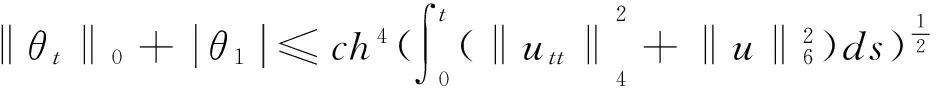
(8)

定理1证毕.

3 超收敛性分析

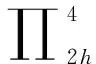
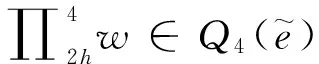
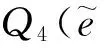
这里ei,di,Zi分别为小单元及它们的边和顶点.

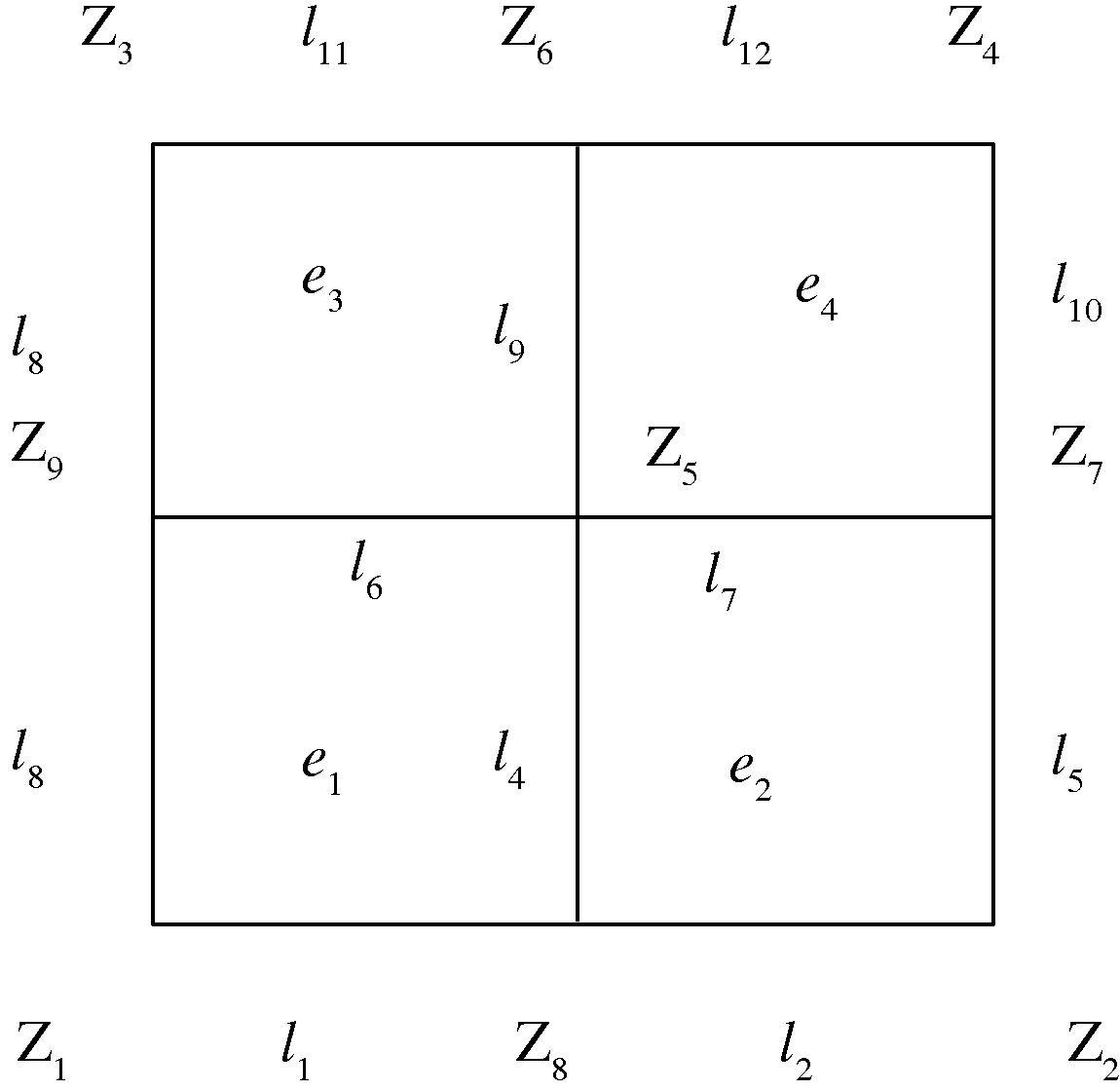
图1 大单元

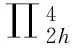
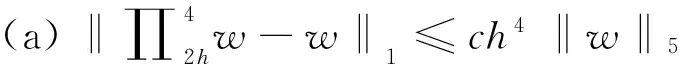
(9)

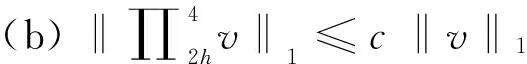
(10)

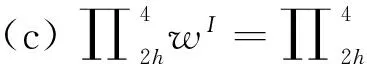
(11)

定理2 在定理1的假设下，我们有如下的整体超收敛结果：

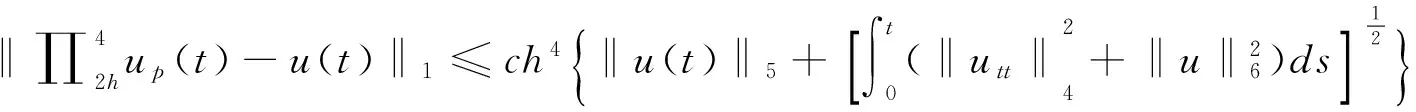
(12)

证明 注意到

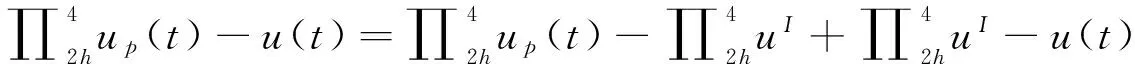
(13)

由式(9)和(11)可知

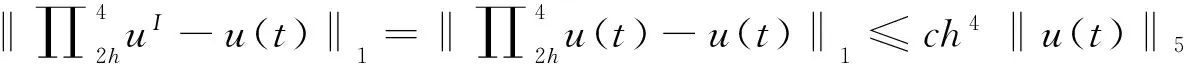
(14)

又由式(10)和定理1有

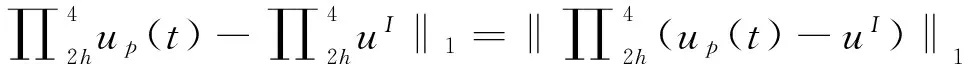
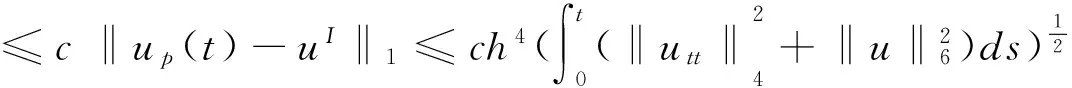
(15)

于是由式(13)、(14)、(15)可得

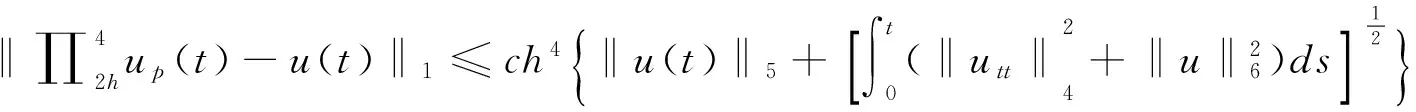
定理2证毕.

[1] 乔中华，陈绍春.窄边双三次 Hermite矩形元[J].郑州大学学报：理学版，2003,35(1):6-10.

[2] 林 群，严宁宁.高效有限元构造与分析[M].保定：河北大学出版社，1996.

[3] 石东洋，谢萍丽，陈绍春.双曲积分微分方程的各向异性非协调有限元逼近[J].应用数学学报，2007，30(4)：654-666.

[4] Liu X Q. High accuracy methods for fully discrete galerkin approximation of parabolice quations[J]. BeijingMathemetics，1995，1(2)：31-36.

[5] 石东洋，梁 慧.一个新的非常规 Hermite型各向异性矩形元的超收敛分析及外推[J].计算数学，2005，27(4)：369-382.

[6] Chen S C, Shi D Y, Zhao Y C. Anisotropic interpolation and quasi-Wilson element for narrow quadrilateral meshes[J].IMA J Numer Anal， 2004, 24: 77-95.

责任编辑：周 伦

Superconvergence Analysis of Anisotropic Finite Element in Second-order Hyperbolic Problem

MA Guo-feng

(SchoolofMathematicsandStatistics，XuchangUniversity，Xuchang461000，China)

Avoiding the regularity assumption (or Quasi-uniform assumption) usage as a limitation in mesh division of finite elements, second-order hyperbolic problem was studied by using anisotropic bilinear element. With integral identity and the interpolation postprocessing techniques, superclose property and superconvergence were derived on anisotropic meshes.

anisotropic meshes, superclose, superconvergence

2015-10-13

马国锋(1971—),男，河南许昌人，副教授，硕士，研究方向：有限元方法及应用．

1671-9824(2016)02-0015-04

O241．21

A