起伏湿气管路持液率和压降计算模型
2016-04-13王文光颜慧慧曲兆光刘春雨万宇飞
王文光,颜慧慧,曲兆光,刘春雨,万宇飞
1.中海石油(中国)有限公司天津分公司,天津 300452
2.中石化天津石油分公司,天津 300100
起伏湿气管路持液率和压降计算模型
王文光1,颜慧慧2,曲兆光1,刘春雨1,万宇飞1
1.中海石油(中国)有限公司天津分公司,天津 300452
2.中石化天津石油分公司,天津 300100
湿气集输管道在天然气开发中发挥着重要作用,如果湿气管道内存在积液,会导致能耗增加、腐蚀加剧和生成水合物等问题,但目前尚没有一个瞬态两相流模型能够准确地计算起伏湿气管道中的积液和压降规律。在已有的两相流双流体模型基础上,基于连续性方程和动量方程,建立了一种新的适用于起伏管路的瞬态两相流理论模型,并利用数值方法通过编制MATLAB程序实现对起伏湿气管道中持液率及压降等的计算。利用普光气田现场湿气集输管道的运行数据对模型进行了验证,并与多相流软件OLGA的模拟计算结果进行了对比。验证结果证明所建立的模型计算精度较高,持液率和压降的相对误差分别为±15%、±5.5%,可以应用于起伏湿气管道两相流的模拟。
起伏湿气管路;瞬态两相流模型;持液率;压降
湿气集输管道中如果存在积液会导致能耗增加,腐蚀加剧,同时还存在生成水合物的风险[1];而在复杂的地形条件下,管道的起伏对管内两相流流型、气液相相间作用有很大的影响,从而导致积液规律等问题更加复杂化。因此,探索起伏湿气管道内的持液率和压降计算方法,对预防管道积液,提高管道输送效率和安全性,具有十分重要的意义[2]。
近年来许多学者对起伏管道内的两相流机理和流动规律进行了实验及理论研究,提出了若干适用于起伏或者倾斜管路的两相流理论模型。
1991年,Wood提出一种适用于起伏凝析气管道的机理模型[3],该模型以实验为基础,是一种一维准稳态模型。模型可以计算出能够带走管道低洼处积液的临界气体速度、最大稳定段塞长度以及初始段塞特性。Zheng通过研究总结了两相流管路的起伏对流动的影响[4],并针对单个起伏管道提出了一种段塞跟踪的理论模型[5],研究了单个起伏管道中段塞的流动特性。1995年,Henau与Raithby提出了一种适用于多起伏管道的段塞流模型[6],提出了关于阻力系数和虚拟质量力的新关系式,并利用实验进行了验证。
宋立群、李玉星针对复杂地形条件下的低含液率管道[7],提出了稳态的水力计算模型,给出了凹面湿壁分数、摩擦因子等参数的计算式。喻西崇等人针对起伏管道对多个持液率计算相关式进行了比较[8],包括Eaton相关式、Dukler II相关式、BB相关式等,给出了各相关式适用的倾角范围。
国内外对起伏管路两相流的研究现状表明,管道起伏对气液两相流流型、气液相分布和管道压降等具有十分显著的影响,但目前尚没有一个较好的模型能够准确地预测复杂多起伏湿气管道内的流动特性,且多数两相流模型是建立在稳态工况条件之上的,对起伏管道内瞬态模型的研究较少。
1 瞬态两相流理论模型
为实现对起伏湿气管路中持液率和压降等参数的计算,本文将结合已有的双流体模型,针对起伏管路中常见的流型,选择合适的闭合关系式,建立适用于绝热条件下的瞬态气液两相流的理论模型。
1.1 基本方程
两相流瞬态模型的建立以流体力学基本守恒方程为基础,作出以下假设[9]:
(1)认为管道处于绝热条件下,可忽略能量方程。
(2)管道内气体可以近似作为理想气体处理。
(3)不考虑相变与相间传质。
根据以上假设,两相流中k相(k=g表示气相、k=l表示液相)的连续性方程和动量方程分别为:

式中:A为管道截面积,m2;t为时间,s;αk为k相占管道截面积的比例;ρk为k相密度,kg/m3;uk为k相速度,m/s;S′mk为单位长度上的质量源项,kg/(s·m);Pk为k相压力,Pa;x为长度,m;Fkx为单位质量力,N/kg;Tkw为k相与管道壁面通过剪切力产生的单位面积动能交换,N/m;Tki为k相在相界面处的单位面积动能交换,N/m;x为x位置处的单位向量;k为k相界面单位向量,l=-g;l、g分别为气、液相界面单位向量;τkw为k相壁面剪切应力,N/m2;ΔPki为k相在相界面处的压力差,Pa;P′ki为k相由于相对速度导致的压力波动,Pa;τki为k相在相界面处的剪切应力,N/m2;Pgi、Pli为气、液相局部界面压力,Pa;τgi、τli分别为气、液相在相界面处的剪切应力,N/m2;σ为相界面表面张力,N/m;Ri为相界面平均曲率半径,m。
1.2 闭合方程
1.2.1 分层流
为推导分层流闭合方程,需要作出以下假设(见图1):第一,假设分层流中气液界面为水平界面。第二,假设气液相界面的曲率半径足够大,表面张力作用可以忽略。第三,忽略相界面压力波动P′ki。

图1 分层流气液相分布
可以得出分层流的闭合方程为[9]:
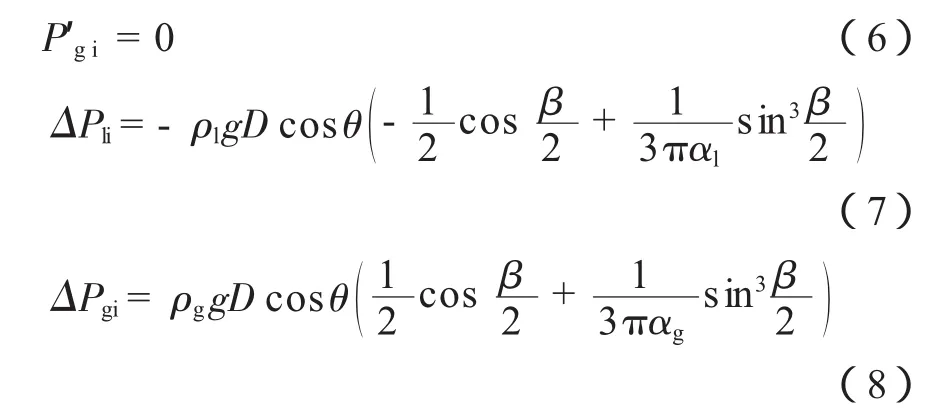
式中:P′gi为由于相对速度导致的气相压力波动,Pa;ΔPgi、ΔPli分别为气、液相在相界面处的压力差,Pa;ρg、ρl分别为气、液相密度,kg/m3;g为重力加速度,取9.8 m/s2;αg、αl分别为气、液相占管道截面积的比例。
假设k相与壁面的剪切力沿Ckw(k相在截面内与管壁的交线,m)不变,则k相与壁面的单位面积动能交换可以写作:

式中:Sk为k相的湿周,m;fk为k相壁面摩擦系数。
k相壁面摩擦系数fk的计算公式[10]:
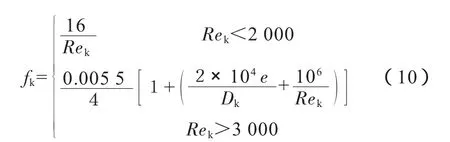
当2 000≤Rek≤3 000时,取上述两者中计算值较大者。
式中:e为管壁粗糙度,m;Rek为k相雷诺数;Dk为k相水力直径,m。
气液界面处的单位面积动能交换等于界面处的剪切应力:
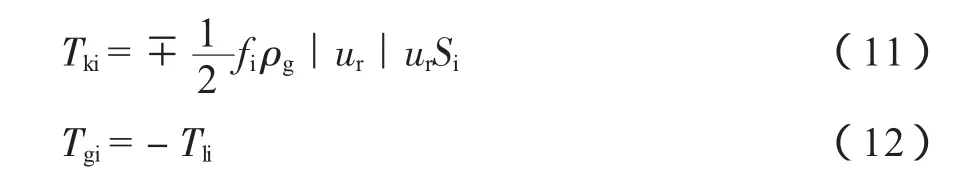
式中:Tgi、Tli分别为气、液相在相界面处的单位面积动能交换,N/m;fi为界面摩擦系数;ur为相对速度,m/s,ur=ug-ul,当ug>ul,气相产生压力降,反之液相产生压力降。
界面摩擦系数fi选用Andritsos[11]所提出的计算公式:
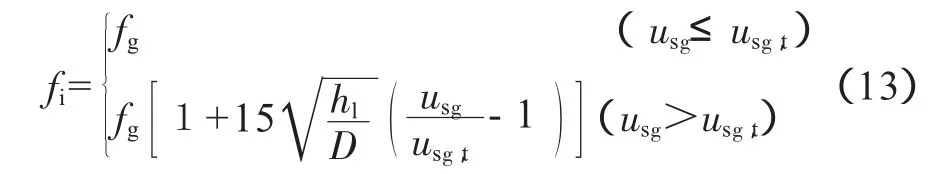
式中:fg为气相壁面摩擦系数;usg为气相表观速度,m/s;usg,t为临界气相表观速度,m/s;hl为稳态分层流液膜厚度,m。

式中:P为系统压力,Pa。
1.2.2 环状流
环状流的闭合方程为:

由于认为环状流的液膜很薄,所以可以认为相平均压力[Pk](Pa)等于界面平均压力Pi(Pa),故可得:

环状流中壁面摩擦系数与分层流公式相同,即公式(9)、(11)。
界面摩擦系数fi按照下面的公式计算[12]:
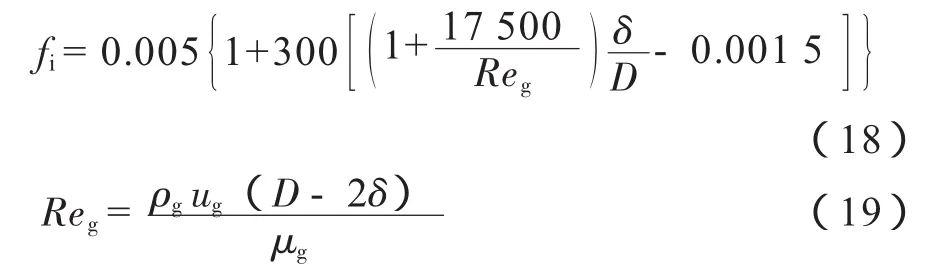
式中:Reg为气相雷诺数;δ为分层流液膜厚度,m;μg为气相动力黏度,Pa·s。
1.2.3 分散流
为了便于推导,方程中使用下标d表示分散相,下标c表示连续相。
假设管道截面内分散相的压力等于连续相的压力,即:

式中:Pc、Pd分别为连续相、分散相平均压力,Pa。
根据上述假设,气液界面动量方程可以化简为:

式中:Tci、Tdi分别为连续相、分散相在相界面处的单位面积动能交换,N/m。
Stuhmiller给出了分散流界面处Tci的表达式:
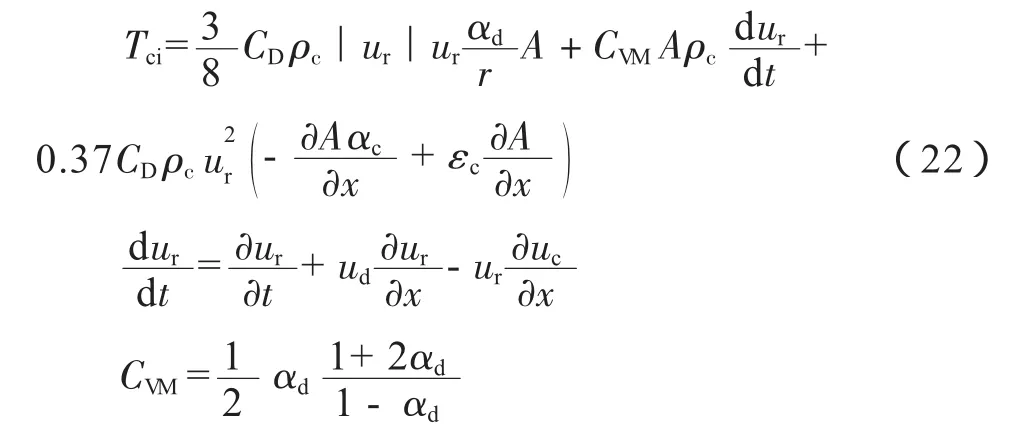
式中:CD为阻力系数,按照文献[13]中的方法计算;ρc为连续相密度,kg/m3;ur为相对速度,m/s,ur= ud-uc;uc、ud分别为连续相、分散相速度,m/s;αc、αd分别为连续相、分散相占管道截面积的比例;r为分散相半径,m;CVM为虚拟质量力系数;εc为连续相湿壁系数,对于均匀分布的混合物,εc=αc;dur/dt为迁移导数,m/s2。
分散流壁面剪切力依然使用公式(9)计算。
1.2.4 段塞流
对于段塞流,假设一个段塞内的压力不变,气、液相压力均等于截面上的平均压力Px,即:

式中:[Pg]、[P1]分别为气、液相平均压力,Pa。
与分散流类似,段塞流界面动量方程可以化简为:

参考公式(22),段塞流中Tli的表达式可以化简为:
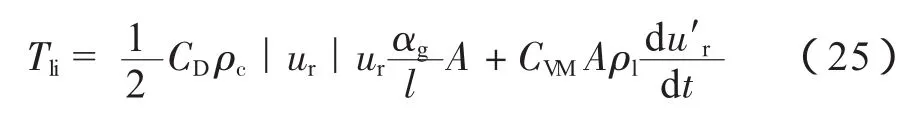
式中:l为段塞总长度l=ls+lf,m,;ls、lf分别为液塞和液膜段的长度,m;ur为气相与液相之间的平均相对速度,m/s;u′r为段塞平移速度vt与液膜速度vlf之差,u′r=vt-vlf,m/s。
段塞流中,流体壁面剪切力应该分别计入液塞段和液膜段的壁面剪切力[14],因此一个段塞内的剪切应力可以写为:
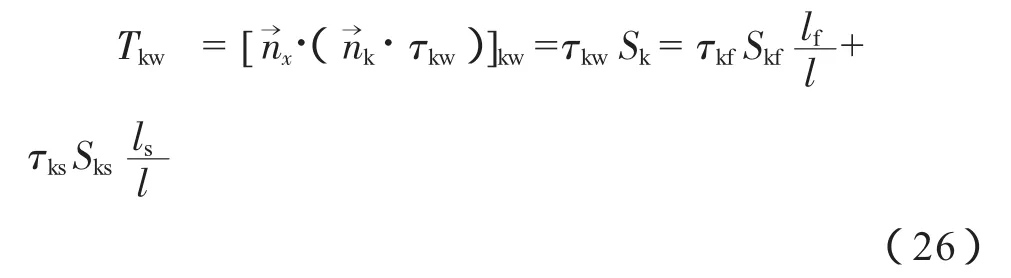
式中:τkf、τks分别为液膜段、液塞段k相的剪切应力,N/m2;Skf、Sks为液膜段、液塞段k相湿周,m。
1.3 气体状态方程修正
对于压力较高的气田集输管道,理想气体的假设会带来较大误差,因此需要对模型进行修正。
考虑到天然气组分较为复杂,采用BWRS方程对模型中气体密度的计算进行修正。BWRS方程形式如式(27) 所示[15-16]:
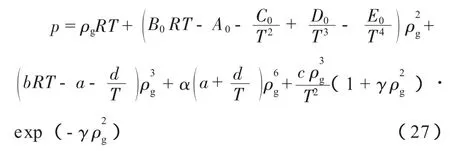
式中:p为系统压力,kPa;R为通用气体常数,R= 8.314 J/(mol·K);T为系统温度,K;A0,B0,C0,D0,E0,a,b,c,d,α,γ为状态方程的11个参数,具体计算方法请参考文献[17]。
由于BWRS方程形式十分复杂,如果采用线性化、离散的处理办法会大大增大程序的复杂程度,导致计算速度降低,因此程序中采用延时修正的方法,即先假设气体为理想气体(压缩因子Z=1),计算出各点压力后,再利用计算出的压力值计算气体密度和压缩因子,然后在循环过程中不断更新压缩因子,从而达到对气体密度的修正。
2 现场起伏湿气管道数据验证
普光气田采用湿气集输系统,管道内气、液相并存[18],由于受地形影响,管道起伏比较剧烈,管道内两相流动较为复杂,因此探究管道内气液两相流流动规律对管路的优化设计和经济、安全运行具有十分重要的意义。
图2为普光气田P201集气站至集气末站的管道高程图[19],从图中可以看出,管道起伏剧烈,管道最大的倾角可以达到47.8°。
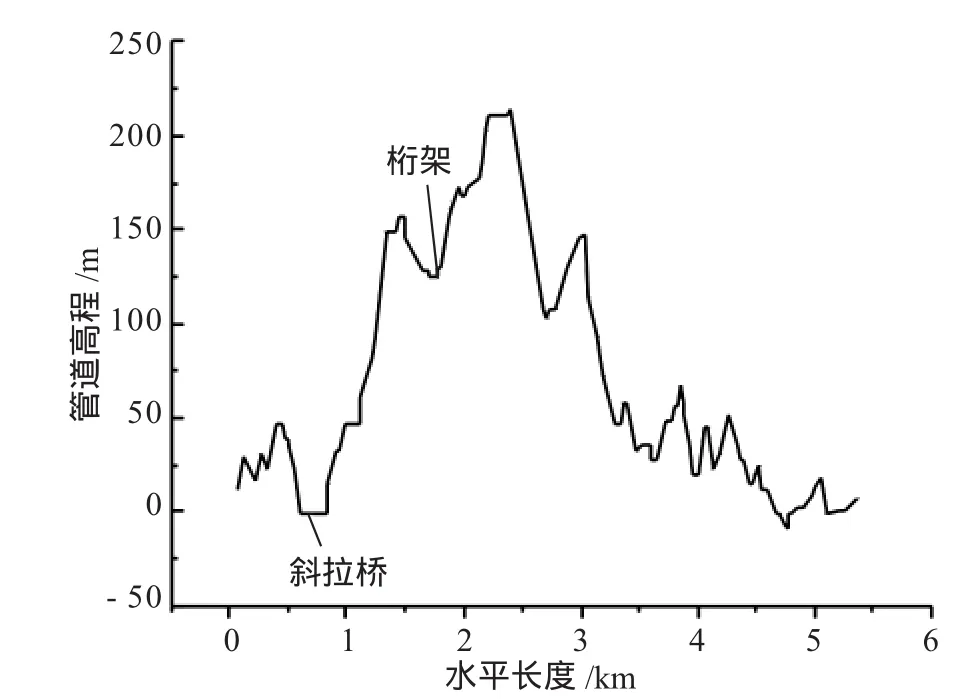
图2 普光气田P201-集气末站管道高程
为了验证本文模型的可靠性,利用该管道的现场运行数据对模型的计算结果进行验证,同时与瞬态多相流软件OLGA的计算结果进行对比,结果见表1和表2。
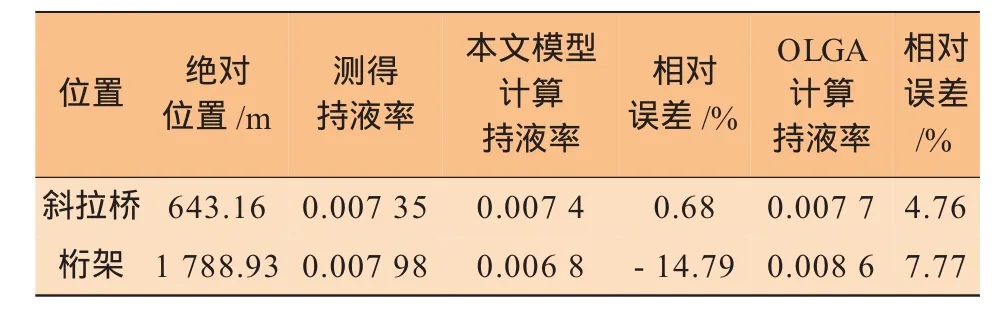
表1 持液率计算结果与测量值对比
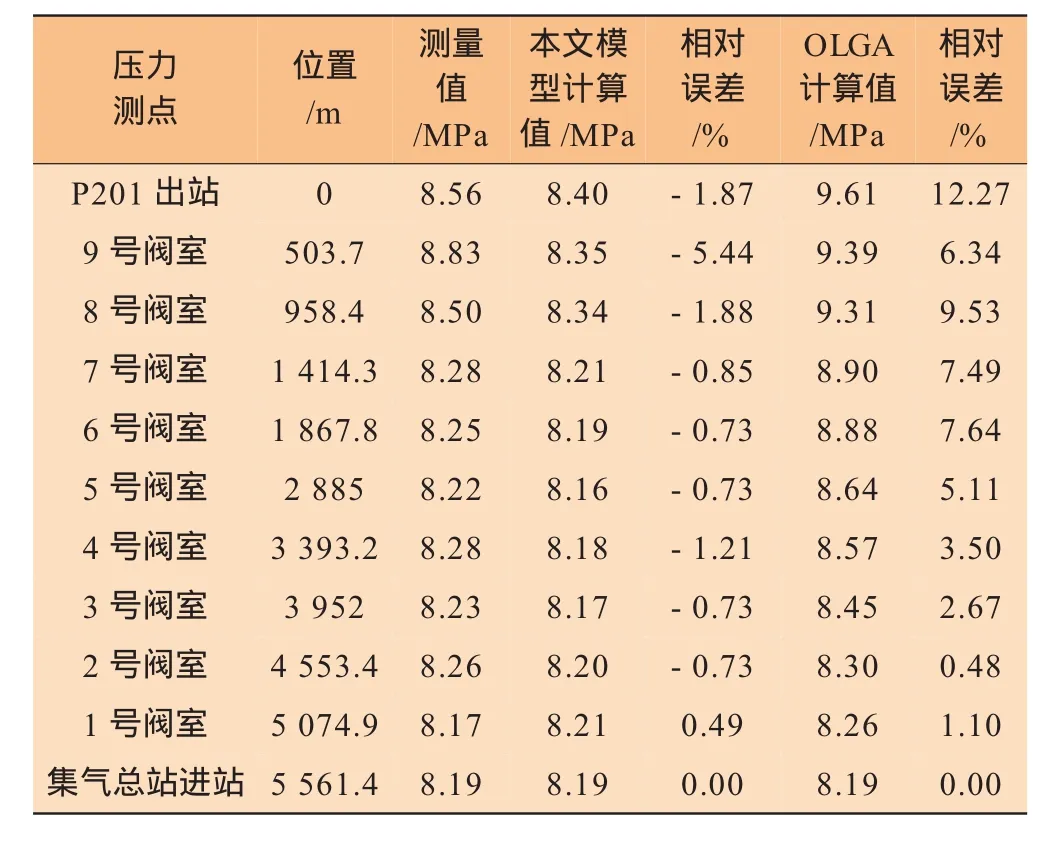
表2 管道压力分布计算结果与测量值对比
从表1管道持液率的计算结果分析,本文模型和OLGA软件对管道持液率的计算结果误差均在±15%以内,能够很好地预测管道内液相分布规律。
从表2中可以看出,OLGA软件计算的管道压力结果普遍偏大,原因是OLGA对流型的判断准确性较差,由于在较大范围内存在段塞流,因此导致管道压力升高。由于引入了BWRS方程对气体密度进行修正,本文模型对管道压力的计算精度明显提高,相对误差均在±5.5%以内。
3 结论
与现场多起伏湿气管道实际运行数据的对比表明,本文的瞬态两相流模型能够很好地模拟起伏湿气管道内的两相流流动,其中,采用本文模型计算持液率的计算精度为±15%,压力计算精度可达±5.5%,与OLGA计算结果相比,本文模型对压力的计算精度更高,两者对持液率的计算精度相近。
[1]张钦杰.气液两相流管道振动机理研究[D].青岛:中国石油大学(华东),2009.
[2]周良胜.复杂地表条件下天然气集输管线积液规律研究 [D].青岛:中国石油大学(华东),2009.
[3]WOOD D.Mechanistic modeling of terrain-induced slugs in gas/condensate lines[C]//Proceedings of BHRG Multiphase Conference.Cannes,France:BHRG,1991.
[4]ZHENG G.Two-phase slug flow in hilly terrain pipelines[D]. Tulsa,US:University of Tulsa,1991.
[5]ZHENG G,BRILL J P,TAITEL Y.Slug flow behavior in a hilly terrain pipeline[J].International journal of multiphase flow,1994,20(1):63-79.
[6]De HENAU V,RAITHBY G D.A transient two-fluid model for the simulation of slug flow in pipelines—I.Theory[J]. International journal of multiphase flow,1995,21( 3):335-349.
[7]宋立群,李玉星.复杂地形条件下气液两相混输工艺水力模型建立[J].化工学报,2012,62(12):3 361-3 366.
[8]喻西崇,赵金洲,冯叔初.起伏多相流管路持液率计算方法研究[J].西南石油学院学报,2000,22(3):94-97.
[9]DE HENAU V.A study of terrain-inducedsluggingin two-phase flow pipelines[D].Waterloo,Canada:University of Waterloo,1992.
[10]BENDIKSEN K,MAINES D,MOE R,et al.The Dynamic Two-Fluid Model OLGA:Theory and Application[J].Spe Production Engineering,1991,6(2):171-180.
[11]ANDRITSOS N,HANRATTY T J.Influence of interfacial waves in stratified gas-liquid flows[J].AIChE Journal,1987,33(3):444-454.
[12]FORE L B,BEUS S G,BAUER R C.Interfacial friction in gas-liquid annular flow:analogies to full and transition roughness [J].International Journal of Multiphase Flow,2000,26(11):1 755-1 769.
[13]ISHII M,MISHIMA K.Two-fluid model and hydrodynamic constitutive relations[J].Nuclear Engineering and Design,1984,82(84):107-126.
[14]曹学文,周鹏.油气水三相段塞流的压降研究[C]//中国工程热物理学会多相流学术会议论文集.重庆:中国工程热物理学会,2006.
[15]STARLING KE,HAN M S.Thermo data refined for LPG--14. Mixtures [J].Hydrocarbon Processing,1972,51( 5):129-132.
[16]苑伟民.修改的BWRS状态方程[J].石油工程建设,2012,38(6):9-12.
[17]吴玉国,陈保东.BWRS方程在天然气物性计算中的应用[J].油气储运,2003,22(10):16-21.
[18]李玉浩,曹学文,雷毅,等.基于超声回波特性的湿气集输管线积液检测技术[J].石油学报,2013,34(6):1 200-1 205.
[19]李玉浩,曹学文,梁法春,等.多起伏湿气集输管线工艺计算方法优选[J].天然气工业,2013,33(8):114-118.
Calculation Model of L iquid Holdup and Pressure Drop in Undulating Wet-gas Gathering Pipeline
WANG Wenguang1,YAN Huihui2,QU Zhaoguang1,LIU Chunyu1,WAN Yufei1
1.CNOOC Tianjin Company,Tianjin 300452,China
2.Sinopec Tianjin Company,Tianjin 300100,China
Wet-gas gathering pipeline plays an important role in natural gas development.Liquid accumulation in the wet-gas pipeline will result in higher energy consumption,corrosion and more hydrates.However,the prediction of the flow behavior in the undulating wet-gas pipeline is difficult,thus no accurate modelis available now.Based on the existing two-phase flow model,a transient two-phase flow model applicable for the undulating wet-gas pipeline is developed in this paper.AMATLAB code is developed and applied to simulate the flow in wet-gas pipeline.In order to testify the accuracy of the model,the liquid holdup and pressure drop of the wet-gas gathering pipeline in Puguang Gas Field are calculated with the errors of±15%and±5.5%respectively.The results are also compared with those calculated by OLGA,which shows the modelcan be applied to simulate the two-phase flow in undulating wet-gas gathering pipeline.
undulating wet-gas pipeline;transient two-phase flow model;liquid holdup;pressure drop
10.3969/j.issn.1001-2206.2016.06.001
王文光(1989-),男,山东滨州人,助理工程师,2015年毕业于中国石油大学(华东)油气储运工程专业,主要从事海上油气田开发前期研究、管道安全流动保障工作。Email:wangwg17@cnooc.com.cn
2016-05-24
