无线电时间比对中的时标偏差影响分析
2016-04-13朱陵凤韩春好
朱陵凤,李 超,韩春好,刘 利,郭 睿
(北京卫星导航中心,北京 100094)
无线电时间比对中的时标偏差影响分析
朱陵凤,李超,韩春好,刘利,郭睿
(北京卫星导航中心,北京 100094)
摘要:结合星地无线电双向时间比对基本原理及模型,从机理和特性上分析了时标偏差对星地双向时间比对精度的影响,并利用实测的GEO、IGSO和MEO卫星星地双向时间比对测距值,计算比较了时标偏差对三类卫星的星地双向时间比对结果影响量级。结果表明:时标偏差影响主要体现在伪距变率项和伪距径向加速度项,当时标偏差不大于1 s时,伪距径向加速度项引起的影响可以忽略,1 s时标偏差导致的星地钟差偏差等于伪距变率的1/2;对于不同类型卫星而言,时标偏差对星地双向时间比对结果的影响不同,卫星运动速度越快,时标偏差导致的星地双向时间比对精度降低程度越大。
关键词:无线电时间比对;时标偏差;伪距变率;伪距径向加速度
0引言
伪距作为无线电时间比对的基本观测量,其测量时刻理应准确标记为伪距信号的本地接收时刻,即本地钟面时。如果由于各种可能原因,测量过程中没有给伪距信号打上准确的接收时刻(时标),我们就认为该伪距测量值存在时标偏差,并且该时标的准确性对于观测目标在不断运动的导航卫星而言显得尤为重要[1]。
基于星地无线电双向时间比对的基本原理和计算模型,从两方面阐述了时标偏差对星地双向时间比对的影响,推导了时标偏差与星地双向时间比对结果的数学关系式,并利用不同类型卫星的星地双向时间比对实测数据进行试验验证。
1星地无线电双向时间比对模型
如图1所示,地面站A和卫星S分别在本地钟的控制下产生并发播无线电伪码测距信号,地面站A发射的无线电信号经时延τAS(t)后,在卫星S本地钟面时TS(t)被S星接收,测量得到上行伪距值ρAS(t),同样,卫星S发射的无线电信号经时延τSA(t)后,在地面站A本地钟面时TA(t)被A站接收,测量得到下行伪距值ρSA(t)。
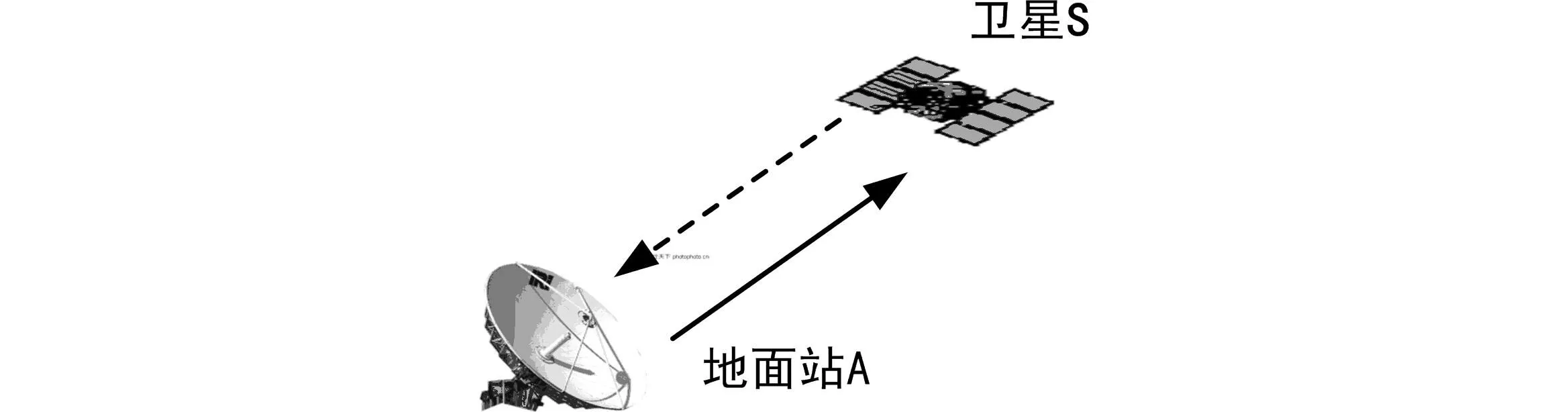
图1 星地双向时间比对示意图
卫星将自己的上行伪距值通过通信链路发送给地面站A,地面站A综合利用本地测量的下行伪距和接收到的上行伪距,解算得到卫星S相对于地面站A的星地钟差ΔTSA(t),从而完成卫星与地面站之间的无线电双向时间比对。其中,t为系统时间。由星地无线电双向时间比对[2-6]的基本原理得出:
ΔTAS(t)=ρAS(t)-CAS-τAS-ΔDAS,
(1)
ΔTSA(t)=ρSA(t)-CSA-τSA-ΔDSA;
(2)
由于ΔTSA(t)=-ΔTAS(t),因此,上两式相减得:
ΔDSA-CAS-τAS-ΔDAS] ,
(3)
上式即为星地无线电双向时间比对基本原理公式,其中,CAS、CSA为上下行几何时延,τAS、τSA为上下行路径上的组合设备时延,ΔDAS、ΔDSA为上下行路径上的电离层、对流层、相对论周期改正、固体潮和测站位移等其他综合延迟量。
2时标偏差影响机理分析
若伪距测量值中存在时标偏差,对星地无线电双向时间比对的影响包括上下行伪距配对错误和单向钟差解算错误两方面。
2.1上下行伪距配对错误
与单向时间比对方法相比,星地无线电双向时间比对的优势在于双向比对过程中抵消上行和下行路径中的公共误差项,而抵消的前提条件就是相同时刻,也就是说,成功配对的上下行伪距测量时刻应该保持一致,如此才能确保配对解算过程中公共误差项基本抵消,以提高星地无线电双向时间比对精度。
若伪距测量值被打上了不准确的时标,即伪距值与测量时刻不相符,会导致配对的上下行伪距的测量时刻并不是真正意义上的一致,导致不同测量时刻的上下行伪距配对成功,与双向时间比对基本原理相悖,简单地说,时标偏差会导致上下行伪距配对错误。
2.2单向钟差解算错误
双向比对钟差是由方向相反的上下行单向钟差互差除以2计算得到,由于卫星轨道随时刻不断变化,因此,与轨道相关的计算项如几何时延、相对论周期改正项等,对时刻信息很敏感。上行路径中的卫星轨道对应时刻为上行伪距测量时刻,下行路径中卫星轨道对应的时刻由下行伪距测量时刻迭代推算得到,也就是说,若伪距测量值存在时标偏差,单向钟差计算式(1)、式(2)中的伪距与后面被减项不匹配,导致单向钟差解算错误,进而导致双向比对钟差结果错误。
3时标偏差影响特性分析
假设地面站A误以为t1时刻的下行伪距ρSA(t1)是t时刻伪距ρSA(t),卫星S误以为t2时刻的上行伪距ρAS(t2)是t时刻伪距ρAS(t),也就是说,上下行伪距测量值中均存在时标偏差。此类情况下,星地相对钟差计算式不再是式(3),而是:

(4)
假设下行伪距中的时标偏差为ΔtA=t1-t,上行伪距中的时标偏差为ΔtS=t2-t,将上下行伪距ρAS(t2)、ρSA(t1)分别在t时刻进行泰勒级数[7,8]展开,保留到二阶项可得:
(5)
(6)
将式(5)、式(6)代入式(4)得:
(7)

对于不同类型卫星而言,伪距变率项量级不同,其中,MEO卫星伪距变率量级最大,其次IGSO卫星,再次GEO卫星,因此,同量级的时标偏差对3种不同类型卫星星地双向时间比对结果的影响量级从大到小依次为MEO卫星、IGSO卫星和GEO卫星。
4实测数据验证分析
为了验证上述理论分析结果的正确性,利用连续3天实测的GEO、IGSO和MEO卫星与北京站的双向时间比对观测数据,分析了伪距变率的变化特性及量级,设定相同量级时标偏差深入分析其对3种不同类型卫星星地双向时间比对结果的影响3类卫星的伪距变率如图2所示。
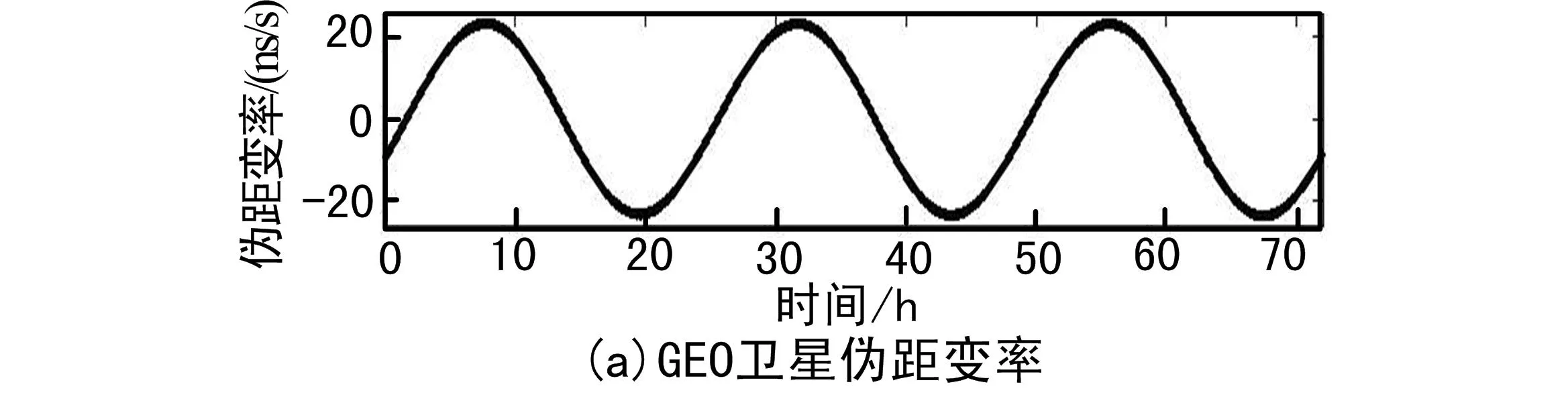
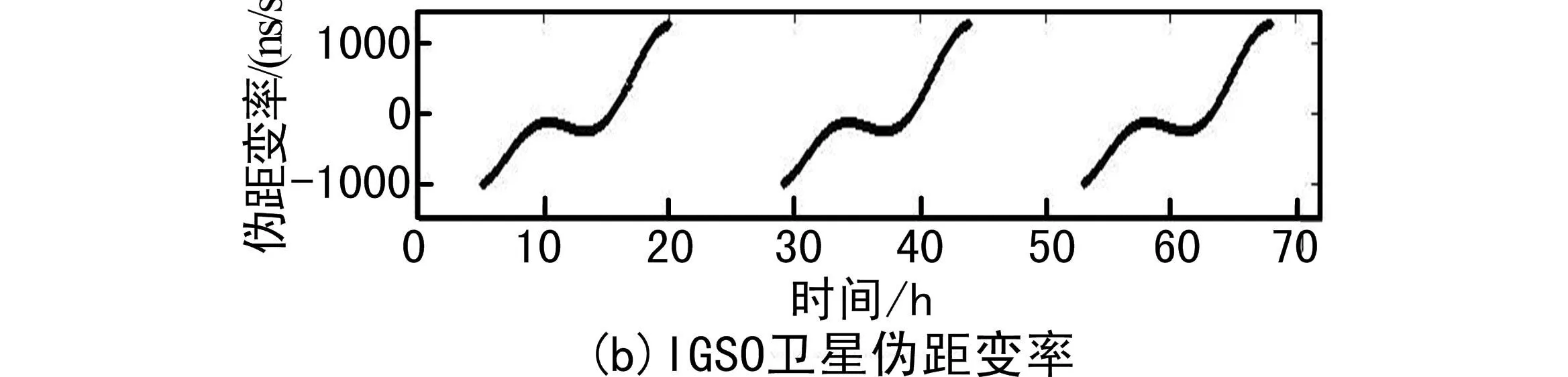
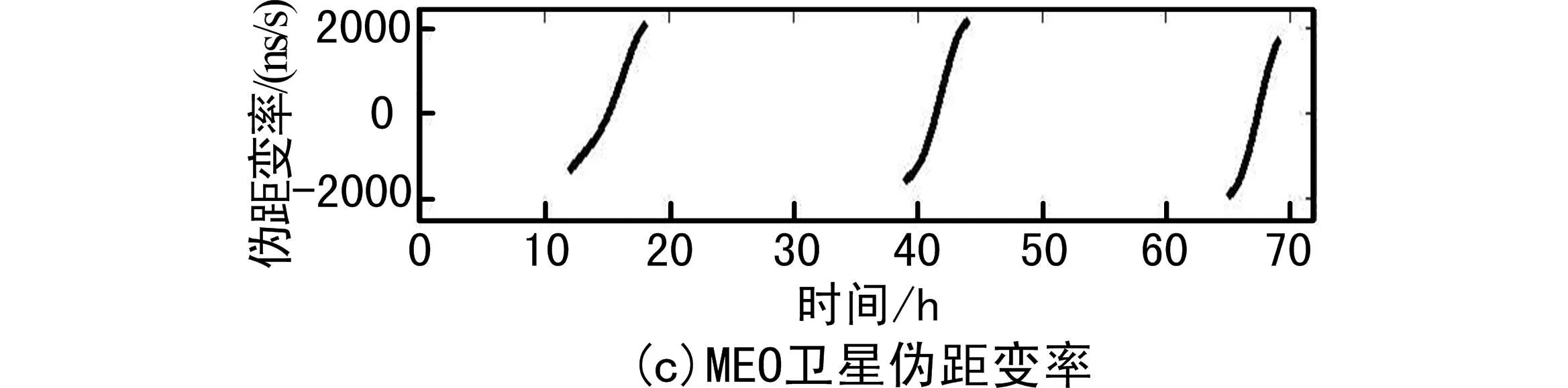
图2 不同类型卫星伪距变率
由图2可见,对于GEO卫星,其多普勒频移引起的伪距变率最大可达约23.35 ns/s,呈现类正弦曲线的变化趋势;对于IGSO和MEO卫星,其多普勒频移引起的伪距变率最大可达约1 266.76 ns/s和2 159.58 ns/s,该影响随着卫星高度角变化不断变化。
假设北京站的下行伪距测量中存在-1 s的时标偏差,计算比较该时标偏差对3种不同类型卫星星地双向时间比对结果的影响。具体方案如下:① 评估有时标偏差与无时标偏差的星地双向时间比对精度,分析时标偏差对不同类型卫星星地双向时间比对精度的影响差异;② 评估时标偏差导致星地相对钟差的偏差与伪距变率项的对应关系,验证上述理论公式的正确性。具体结果如表1和图3所示。
由图3、图4和图5可见:① 无时标偏差情况下,GEO卫星的星地双向时间比对精度约0.68 ns,北京站存在-1s时标偏差情况下,精度下降11倍,达8.27 ns;② 无时标偏差情况下,IGSO卫星的星地双向时间比对精度约0.93 ns,北京站存在-1s时标偏差情况下,精度下降308倍,达287.93 ns;③ 无时标偏差情况下,MEO卫星的星地双向时间比对精度约0.46 ns,北京站存在-1 s时标偏差情况下,精度下降1 273倍,达586.28 ns。
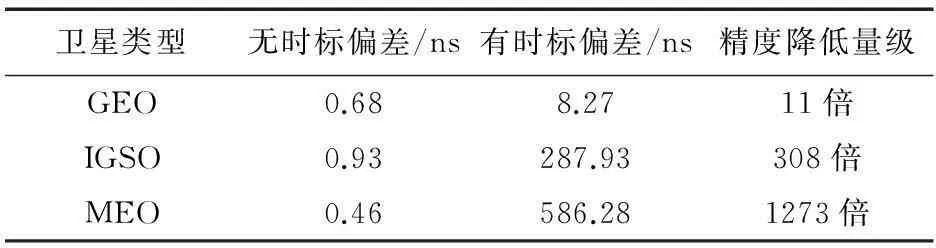
表1 时标偏差对星地双向时间比对精度的影响

图3 GEO卫星星地钟差拟合残差图
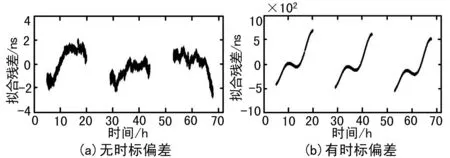
图4 IGSO卫星星地钟差拟合残差图

图5 MEO卫星星地钟差拟合残差图
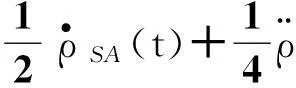
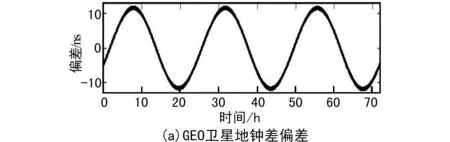
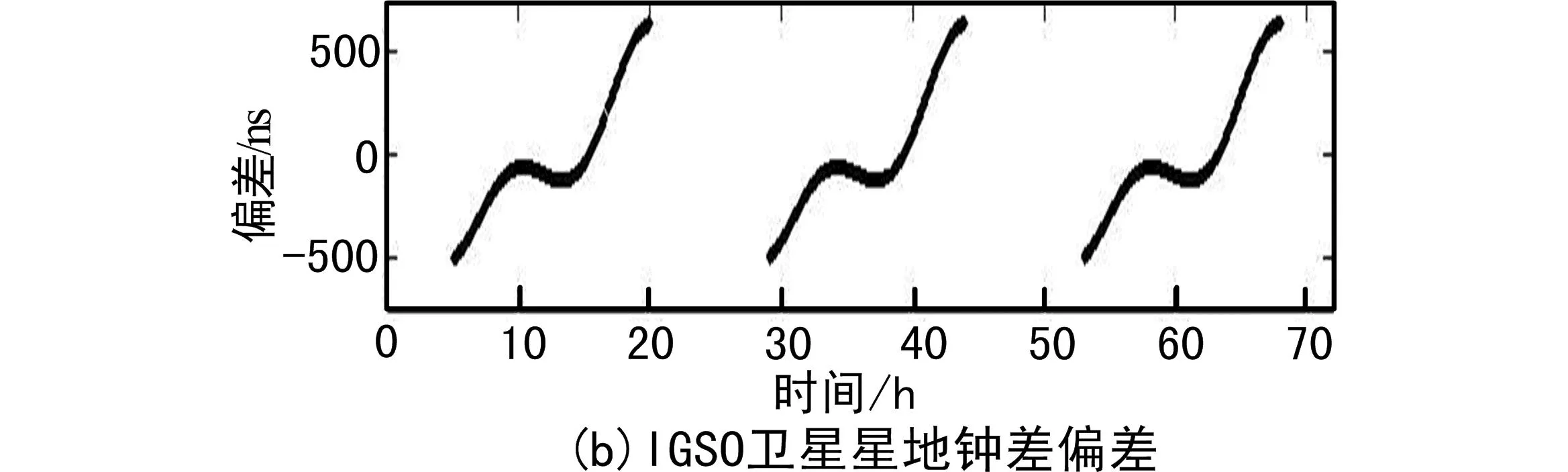

图6 时标偏差导致的星地钟差偏差图
由图6和图2可以看出,北京站-1 s时标偏差导致的星地钟差偏差等于北京站下行伪距变率值的1/2,充分验证了上述理论分析结果的正确性。
5结束语
通过时标偏差对星地无线电双向时间比对的影响机理分析,得知时标偏差会导致星地无线电单向钟差解算错误进而导致双向时间比对结果错误,当时标偏差量级超过1 s时,会导致星地上下行伪距配对错误进而导致双向时间比对结果错误;通过影
响特性分析和实测数据验证,得知时标偏差对星地无线电双向时间比对的影响值主要体现在伪距变率项上,并且卫星运动速度越快,时标偏差导致的星地无线电双向时间比对精度降低程度越大。因此,星地无线电双向时间比对测量过程中应尽可能地避免出现时标偏差问题。
参考文献
[1]韩春好,刘利,赵金贤.伪距测量的概念、定义与精度评估方法[J].宇航学报,2009,30(6):2421-2425.
[2]许其凤.空间大地测量学—卫星导航与精密定位[M].北京:解放军出版社,2001.
[3]夏一飞,黄天衣.球面天文学[M].南京:南京大学出版社,1995.
[4]刘利,韩春好,朱陵凤,等.基于伪距测量的钟差计算模型[J].时间频率学报,2009,6(32):36-41.
[5]刘利,朱陵凤,韩春好,等.星地无线电双向时间比对模型及试验分析[J].天文学报,2009,50(2):189-196.
[6]刘利,韩春好.地心非旋转坐标系中的卫星双向时间比对计算模型[J].宇航计测技术,2004,24(1):34-39.
[7]李志刚,李焕信,张虹.卫星双向法时间比对的归算[J].天文学报,2002,43(4):422-431.
[8]黄维彬.近代平差理论及其应用[M].北京:解放军出版社,1992.
[9]朱陵凤,唐波,李超,等.不同时标偏差对站间双向时间比对的影响分析[J].宇航计测技术,2008,5(5):39-41.
[10]刘利,唐桂芬,郭睿,等.伪距测量中的时标偏差影响分析[J].时间频率学报,2012,4(35):105-111.
Influence Analysis of Timescale Deviation on Radio Time Transfer
ZHU Ling-feng,LI Chao,HAN Chun-hao,LIU Li,GUO Rui
(Beijing Satellite Navigation Center,Beijing 100094,China)
Abstract:This paper analyzes the influence of timescale deviation on time transfer processing precision from mechanism and characteristic combining with the basic principle and model of satellite-earth two-way radio time transfer.By using measured ranging values of satellite-earth two-way time transfer of GEO,IGSO and MEO satellites,the influence magnitude of timescale deviation on satellite-earth two-way time transfer of these three satellites is calculated and compared.The results show that the influence of timescale deviation is mainly from pseudorange variability and pseudorange radial acceleration.When the timescale deviation is more than 1s,the influence from pseudorange radial acceleration can be ignored,and the satellite-earth clock deviation of 1s timescale deviation is half of pseudorange variability.For different types of satellite,the influence of timescale deviation on satellite-earth two-way time transfer results is different.The higher the satellite velocity is,the higher the influence magnitude is.
Key words:radio time transfer;timescale deviation;pseudorange variability;pseudorange radial acceleration
中图分类号:TN927
文献标识码:A
文章编号:1003-3114(2016)02-66-4
作者简介:朱陵凤(1983—),女,工程师,主要研究方向:卫星导航与无线电时间比对技术。李超(1981—),男,工程师,主要研究方向:卫星导航用户终端算法研究。
基金项目:国家高技术研究发展计划(863 计划)(2013AA122402;2014AA123102)
收稿日期:2015-09-17
doi:10.3969/j.issn.1003-3114.2016.02.17
引用格式:朱陵凤,李超,唐波,等.无线电时间比对中的时标偏差影响分析 [J].无线电通信技术,2016,42(2):66-69.
