一种基于频率相关的MPSK信号检测方法

杜　谦

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)



一种基于频率相关的MPSK信号检测方法

杜谦

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

摘要：针对负信噪比条件下MPSK通信信号的盲检测问题，通过对MPSK信号频域特性进行理论分析，提出了一种基于频率相关的MPSK信号检测方法。该方法利用MPSK信号的相位变换状态有限而造成频域上谐频分量对称的特点，采用频率相关方法，将信号由于相位翻转而产生的频率谐波分量集中起来，从而获得较高的处理增益，能够在负信噪比下实现MPSK信号的快速搜索和截获。理论分析和工程实践均证明了该算法的有效性和正确性。

关键词：负信噪比；频率相关；MPSK信号；盲检测

0引言

至今为止，卫星通信、对流层散射通信和无线移动通信等领域为了达到更高的数据传输性能，仍普遍采用相位键控信号(MPSK)调制。因此，在通信侦察或智能接收系统中需要对MPSK进行精确的检测和参数估计。目前，MPSK的盲检测和盲识别算法中存在一个迫切需要解决的问题，就是如何利用MPSK信号的周期平稳特性来抑制背景噪声，实现负信噪比情况下对MPSK信号的快速搜索和截获，达到能够有效降低信号检测门限的目的。近年来，有许多文献提出了基于周期谱[1-3]、基于星座图聚类法[4，5]和基于信号二次方谱相关特征法[6]等来实现MPSK信号盲检测[7-9]或盲识别的算法[10-12]，但这些方法存在无法适应低信噪比的要求、运算复杂度大等问题。

针对这一问题，提出了一种基于频率相关的MPSK信号盲检测方法。该方法利用MPSK信号的相位变换状态只有几种有限的情况，通过频率相关的方法可以将信号由于相位翻转而产生的频率谐波分量能量更集中起来，从而在信号的幅度谱上形成锐利的尖峰，以获得较高的处理增益。该方法可以在负信噪比条件下快速搜索并确定MPSK信号的存在，且运算简单，适应性好，抗噪声能力强，对不同调制阶数、不同成形滤波系数的MPSK类调制信号均适用。

1MPSK信号的频域特性分析

首先，以BPSK信号为例来研究MPSK调制信号的频域特性。众所周知，BPSK信号的调制倍数M为2，其信息相位可取的φ(t)值分别为0或π，显然，BPSK信号有2种状态：

S0(t)=S·cos(ω0t+φ0) ，

(1)

S1(t)=S·cos(ω0t+π+φ0)=-S0(t)；

(2)

若将BPSK 信号以具有2个正交脉冲的集合来表征，则：

Si(t)=S·Ai(t)cos(ω0t+φ0)，

(3)

式中，Ai(t)是确定频谱包络的信号，取值-1或1。分解后，信号Si(t)可以表示为频谱上多个谐波分量之和的形式。即：

(4)

(5)

和

(6)

这2组频谱分量对称地出现在载波频率ωо的两侧，而且呈现出复共轭的特性。这些相对于ωо的对称的成对谱分量的积，均是实数。即：

(7)

而且，任何其他的、不与载波频率ωо相对称，而与任何一个其他频率ωm≠ω0对称的谱对数，即：

(8)

上式是一复合数。这些分量之和的极限为：

(9)

N愈大，且在极限内等于频率相关函数的最大值，则相对于ωо对称的谱分量的乘积将愈大：

(10)

式中，Rimax(ω)是频率相关函数的最大值。这样，

(11)

与BPSK不同，QPSK(四相相位键控)调制信号，在符号周期Тс内可取4个离散的相位值(例如，0,π/2,π,3π/2)。这导致它可用4个符号的组合来描述，这些符号用下面的表示式来定义：

S00(t)=S·cos(ω0t+φ0)，

(12)

S10(t)=S·cos(ω0t+π/2+φ0)，

(13)

S11(t)=S·cos(ω0t+π+φ0)=

-S·cos(ω0t+φ0)=-S00(t),

(14)

S01(t)=S·cos(ω0t+3π/2+φ0)=

-S·cos(ω0t+π/2+φ0)=-S10(t)

(15)

通过对QPSK 信号表达式进行分析，可见QPSK信号的符号组成一个双正交的集合。因此，此信号可以表示为2个相互位移π/2的BPSK信号之和。

2基于频率相关的MPSK信号检测及识别算法

通过上节对BPSK和QPSK信号频谱特性的理论分析，可以确定基于频率相关的MPSK信号检测算法，具体步骤如图1所示。

图1　基于频率相关的MPSK信号检测算法流程图

按照图1的计算方法，对BPSK信号进行频率相关函数及其卷积计算，可以得到如图2的最大值谱图结果。图2(a)是BPSK信号的功率谱，显然没有明显的尖锐谱线，而在图2(a)和图2(b)的频率相关函数和卷积之后获得的谱图上，都出现了具有明显的尖锐谱线，且最大值对应的位置就是载波频率。

图2　采用频率相关法对于BPSK信号的检测结果

图3　采用频率相关法对于QPSK信号的检测结果

3性能分析

本节将通过仿真试验验证本文提出方法的性能。试验条件：归一化采样频率下，AWGN信道，伪随机序列调制过的BPSK或QPSK信号，每个脉冲成形波形为升余弦滤波器，每个码元周期内有8个采样点。

试验内容一：测试新方法的检测信噪比门限；

图4给出了在不同信噪比下新方法检测BPSK或QPSK信号的仿真性能结果，试验结果表明该算法在负信噪比下仍能准确地检测到信号。

图4　新方法的BPSK/QPSK信号检测性能测试结果

仿真试验结果表明：采用频率相关法的最小信噪比检测门限为：对BPSK信号，不大于-5.0 dB；对QPSK信号，不大于-3 dB。

试验内容二：测试新方法的测频误差；

频率相关法其测频精度取决于采样率Fs和FFT的点数N，而N点FFT变换的测频精度为：

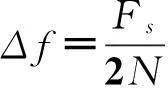
(1)

当采用频率相关法来分析MPSK信号时，频率相关函数输出的信号能量，就是将按所选的离散FFT加窗函数的特性(亦即所得序列乘加权函数)，分布在各离散分量上。这时，相对于载波频率对称的谐波分量仍然是复共轭的。采用频率相关法估计载频时，由于加窗FFT运算而带来的输出信号能量损耗，对于不同类型的窗函数是不一样的。仿真试验表明，矩形窗的频率识别率最高，但其幅度值识别精度最低；此时的最大损耗为：对于BPSK信号，不大于3 dB；对于QPSK信号，不大于6 dB。

试验内容三：BPSK/QPSK调制方式的识别概率。图5给出了在不同信噪比下新方法识别BPSK或QPSK信号的仿真性能结果，试验结果表明该算法在负信噪比下能够正确识别信号。

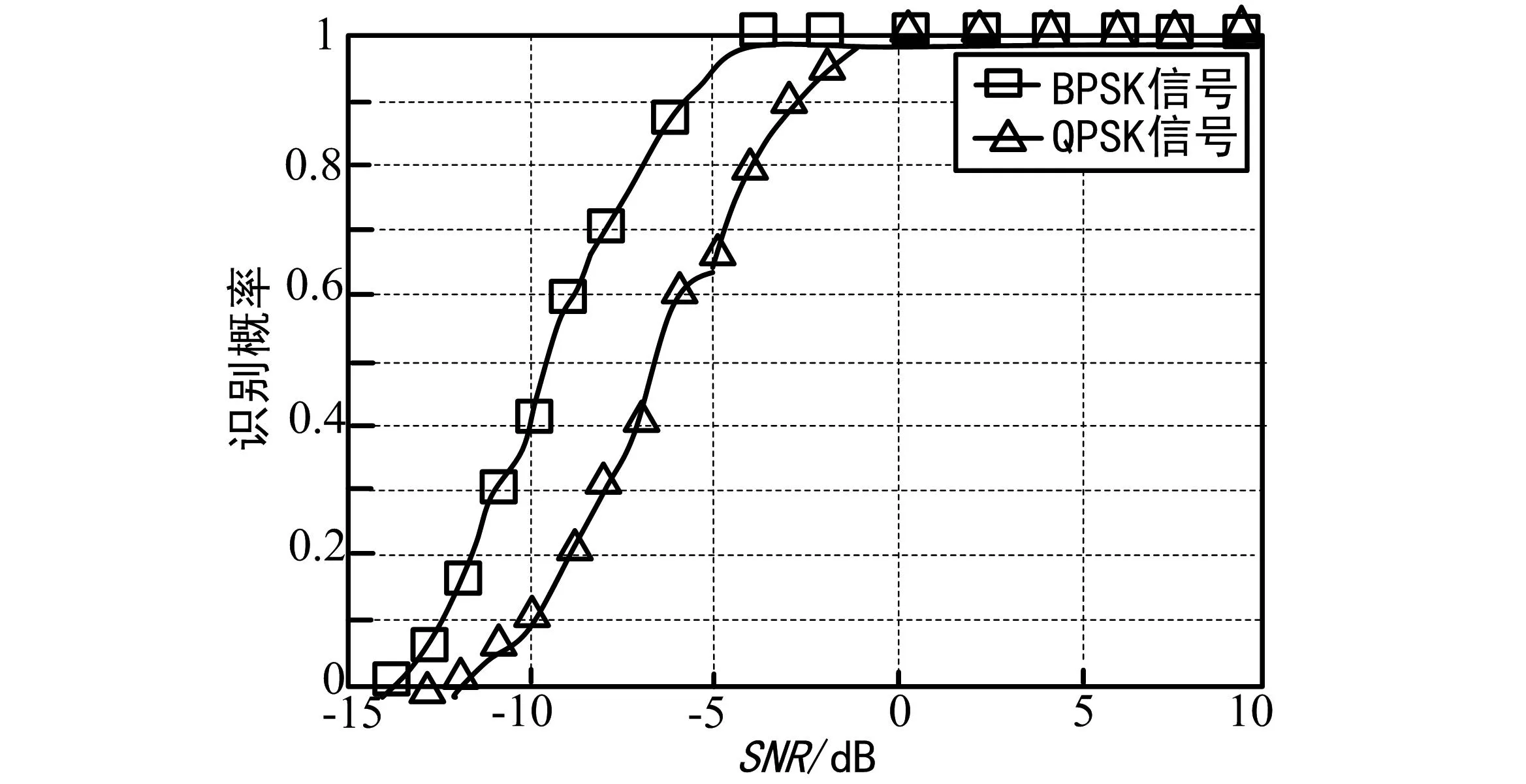
图5　新方法的BPSK/QPSK信号识别性能测试结果

仿真试验结果分析表明：以识别概率达到99%为条件，采用频率相关法进行BPSK或QPSK信号识别时，最小信噪比识别门限为：对BPSK信号，不大于-4 dB；对QPSK信号，不大于-1 dB。

4结束语

本文提出一种基于频率相关的MPSK信号盲检测算法。该方法首先要对MPSK信号进行过采样，通过计算频率相关函数和信号卷积后的频率相关函数，可以将信号由于相位翻转而产生的频率谐波分量能量集中起来，以获得较高的处理增益，进而提取频率相关函数的特征对调制阶数进行识别。该方法不需要任何先验信息，可以在较短的数据长度下得到理想的检测性能。但是它的不足之处是对高阶(m>4)的MPSK的识别能力有限，且检测信噪比要

求较高。总之，本算法为低信噪比下MPSK信号的盲检测提出了一种切实可行的解决方案。

参考文献

[1]韩国栋,蔡斌,邬江兴.调制分析与识别的谱相关方法[J].系统工程与电子技术,2001(23):34-36.

[2]郑鹏,刘锋,张鑫,等.MPSK信号循环谱检测与码元速率估计改进算法[J].电光与控制，2012(8):42-43.

[3]张仔兵,李立萍,肖先赐.MPSK信号的循环谱检测及码元速率估计[J].系统工程与电子技术,2005(5):803-805.

[4]张炜.数字通信信号调制方式自动识别研究[D].长沙：国防科学技术大学,2006:65-145.

[5]徐健飞,汪芙平,王赞基.基于相位聚类的MPSK信号调制分类算法[J].电路与系统学报,2011(5):55-57.

[6]袁本义,于宏毅,田鹏武.基于信号二次方谱相关特征的MPSK调制识别[J].信号处理,2011(4):559-561.

[7]郑纪民，胡亚.一种MPSK信号载频高精度实时估计算法 [J].无线电工程,2012(5):22-23.

[8]李辉,吴争.一种QPSK突发信号的信噪比估计方法[J].无线电工程,2007(9):26-27.

[9]夏辉,靳晓艳.相关运算在信号处理中的应用[J].无线电工程,2014(9):67-69.

[10]白洁,陈健.MPSK/QAM信号自动识别算法的研究[J],电子科技,2008(2):68-70.

[11]邓振淼,刘渝.MPSK信号载频盲估计[J].通信学报,2007(2):95-98.

[12]孟玲玲，侣秀杰.瑞利衰落信道下MPSK信号调制方式识别 [J].无线电通信技术,2008,34(5):59-61.

A Method for Blind Detection of MPSK Signal Based on Frequency Correlation

DU Qian

(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)

Abstract：To solve the problem of blind detection method of MPSK signal in bad condition such as negative SNR,a method for blind detection of MPSK signal based on frequency correlation is presented,in accordance with theoretical analysis of MPSK signal in frequency domain.The method takes full advantage that the symmetrical characteristic of harmonic component as a result of MPSK signal only has several very limited phase transformation states.The method also utilizes frequency correlation to gather frequency harmonic component and win higher processing gain and provides good performance to search and detect quickly MPSK signal under negative SNR.Theoretical analysis and engineering practice prove the availability and validity of the method.

Key words：Negative Signal-to-noise Ratio;Frequency Correlation;MPSK signal;Blind Detection

中图分类号：TN911

文献标识码：A

文章编号：1003-3114(2016)02-44-4

作者简介：杜谦(1973—)，男，高级工程师，主要研究方向：通信对抗、现代信号处理技术和无线通信系统等。

基金项目：国家部委基金资助项目

收稿日期：2015-11-26

doi:10.3969/j.issn.1003-3114.2016.02.11

引用格式：杜谦.一种基于频率相关的MPSK信号检测方法[J].无线电通信技术,2016,42(2):44-47.