基于对称视角的一题多法的研究
2016-04-13山东省栖霞市教体局教研室王志进
☉山东省栖霞市教体局教研室 王志进
基于对称视角的一题多法的研究
☉山东省栖霞市教体局教研室王志进
一、研究一题多法的缘起
一题多法是具有中国特色的数学教育成果之一,它在培养学生的发散思维、提高学生的综合素养及减轻学生的学习负担等方面作用巨大.
笔者在长期的实践与研究中,深感学生解题思路匮乏,不少学生面对教师或教辅给出的精彩纷呈的巧思妙解,往往产生难以企及的自卑感,因此,破解一题多法产生的密码,从而让更多的学生受益,是数学教育者共同面对的难题,也是笔者长期研究的课题.
本文研究的范围仅限于某一知识领域内的、教师在教学中可操作的、学生便于掌握的一题多法,研究策略是基于对称视角下,对这些眼花缭乱的解法之间关系的揭示与梳理,从而揭示一题多法自然产生的密码.
二、探索一题多法的历程
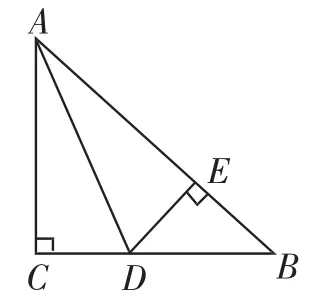
图1
笔者见过不少专著、论文等文献探索一题多法的成因,下面的三个案例引起了笔者的注意.
案例1如下所示.
例1如图1,在△ABC中,AC= BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
反思:这是山教版义务教育课程标准实验教科书数学七年级下册第128页的一个例题,也是初中数学的一个经典题型——求线段之和的问题,课本上的解法很显然是截长法.有经验的老师会补充另一种解法:补短法.
截长与补短,它们之间是怎样的关系呢?它们之间的这种关系能引发我们对一题多法产生怎样的思考呢?
案例2如下所示.
上海教师进修学校的孙琪斌老师早在20多年前就发现有一类题目的证明方法时常成对出现!并于2009年和2010年两次在《上海中学生报》(中招周刊)分别撰文《从一个有趣的证法成对说起》(例2)和《再谈“证法成对出现”》(例3),利用平行线构造A型或X型基本图解决问题的方法成对出现,即过图中的每个点都存在两种利用平行线构造A型或X型基本图的解题方法.
例2(2009年山东潍坊)已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E(如图2).
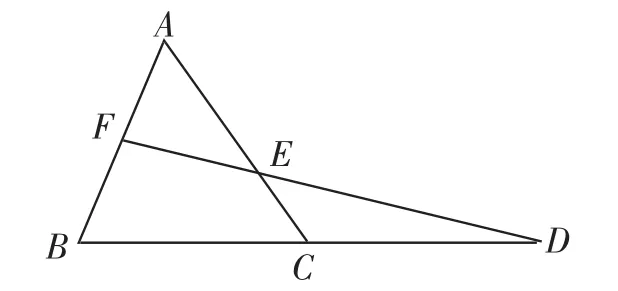
图2
(2)若AB=a,FB=EC,求AC的长.
反思:孙琪斌老师利用自己发现的成对理论,引导学生分别过A、B、C、D、E、F六个点中的任意一个点都可以作两条平行线,共得到十二种解法,
例3(2010年上海)如图3,在Rt△ABC中,∠ACB= 90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与线段BC的延长线交于点P.
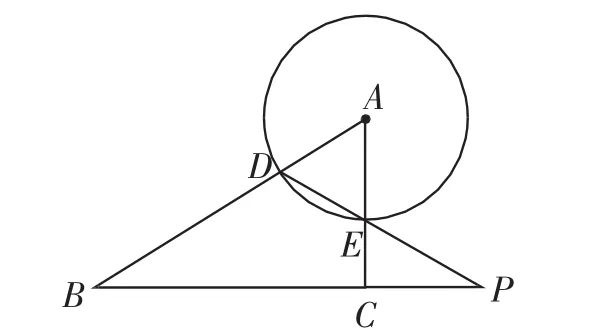
图3
(1)当∠B=30°时,连接AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
反思:2010年上海市初中毕业统一学业考试数学卷第25题中第二、三问也属于这类“证法成对出现”的范畴.引导学生分别过A、B、C、D、E、P六个点中的任意一个点都可以作两条平分线,共得到十二种解法.
案例3如下所示.
列方程解应用题是初中数学的一个难点,学生列一个方程都很难,又怎能实施一题多法呢?特级教师孙维刚发现列方程的一个绝招:选择题目中的任意一个量,然后用两种方式加以表达,并用等号连接,即可以得到方程!
反思:题中的任何一个量既然都可以用两种方式表达,那么这些量之间存在着怎样的关系?
这三个案例都能够形成一题多法,它们的关键词分别是“截长与补短”“过任意一个点都可以作两条平行线,证法成对出现”“任意一个量用两种方式加以表达”!笔者隐隐约约觉得它们之间有着不可言喻的共性.那么这个共性到底是什么呢?应该如何来描述呢?
笔者想到了用“对称”这个词来描述一题多法成因的内核,对称不是指数学、物理等学科上的定义,而是指广义的对称性,即指我们关注的研究对象在解题中的地位相同、功能相似.对称不仅是指已知条件之间的对称,也可以指结论之间的对称及解法之间的对称.
比如,在案例1中线段和的问题,截长与补短在解题中地位一样,由截长联想到补短,能截长就一定能补短,反之,能补短就一定能截长;在案例2中,题目中出现的六个点的地位一样,能过其中一点作平行线,就能过另一点作平行线,能过其中一点作某一方向的平行线,就能过该点作另一方向的平行线;在案例3中,我们可以把其中任意一个量用两种方式加以表达,并用等号连接得到方程.这都是对称思想的具体体现.
例4一艘轮船顺水航行40千米所用的时间与逆水航行30千米所用的时间相同,若水流速度为3千米/时,求轮船在静水中的速度.
分析1:本题是数学中常见的题型——行程问题,根据我们解题经验的积累,常常是求谁设谁.
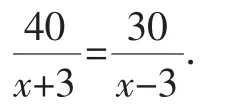
分析2:我们知道,与速度有关的量共有四个:顺水速度、逆水速度、静水速度和水流速度,而水流速度是已知的,另外三个量都是未知的,所以我们认为顺水速度、逆水速度、静水速度这三个量之间应该是对称的,所以也可以采取如下未知数的设法.
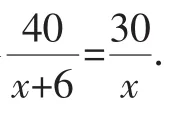
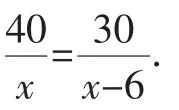
分析3:我们知道行程问题中有三个重要的条件:路程、时间、速度.由于路程已知,所以速度和时间就是对称的,当我们设速度为未知数时,同样也可以设时间为未知数.因为顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度,所以顺水速度-逆水速度=2×水流速度.
分析4:我们利用对称的思想探究了未知数设法的多样性,从而形成了一题多法.由于应用题的求解一般是按照审、设、列、解、验、答“六字诀”进行的,所以我们预测应用题的求解这六个步骤之间也是对称的!
列方程实际上就是运用算两次的思想,把题中的一个量用两种方法表示即可!由于题目中涉及的量共七个:顺水路程、逆水路程、时间、顺水速度、逆水速度、水流速度、静水速度.根据对称性的理论,我们预测每一个量都可以用两种方式来表示.
我们设轮船在静水中的速度为x千米/时,则轮船在顺水中的速度为(x+3)千米/时,轮船在逆水中的速度为(x-3)千米/时为例来说明这个问题,我们还可以列出下面的方程:
我们设轮船在静水中的速度为未知数,就有法1、法5~法12共9种解法,我们还可以设顺水速度、逆水速度或时间为未知数,这样共计形成36种解法的庞大解法体系,让我们再一次领略了基于对称性理论指导下产生一题多法的巨大威力.
例5已知在△ABC中,∠B=2∠C,∠A的平分线AD 交BC边于点D.求证:AC=AB+BD.
分析:这是初中数学常见的截长补短的题型,这个题目比例1更具一般性,因此,笔者选用本题实施对称思想下的一题多法的实践.
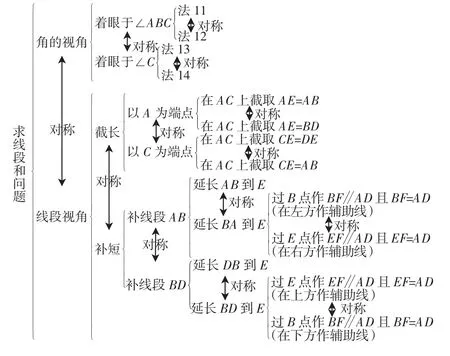
本题主要的解法就是两大类:截长与补短,这两大类解法之间就充分体现了对称的思想.
第一类:截长法(共四种方法).
法1:最常见的解法就是在AC上截取AE=AB,连接DE,然后证明BD=CE(如图4).
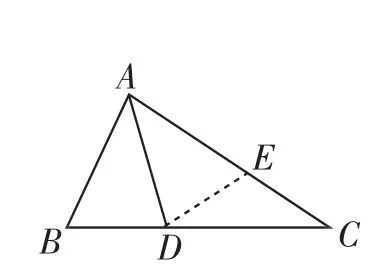
图4
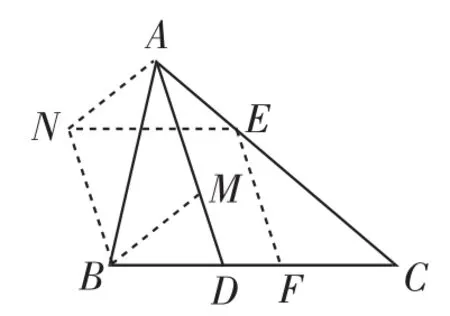
图5
分析1:法1中,我们是在AC上截取AE=AB,根据对称的思想,我们能否在AC上截取AE=BD,然后证明AB= CE?所以产生法2.
法2:在AC上截取AE=BD,然后作∠ABC的平分线BM,交AD于M点,过B点作BN∥AM且BN=AM,连接AN、NE,过E点作EF∥BN,交BC于点F,最后证明AB=CE(如图5).这种截长法思路行得通,要证明比较复杂,图中众多的辅助线可以说明证明过程的艰辛.
分析2:法1和法2是从A点开始截取,根据对称性,我们能否从C点开始截取呢?
法3:在AC上截取CE=BD,然后证明AB=AE(如图6).(法3也等价于作线段DC的垂直平分线,与线段AC交于E点)

图6
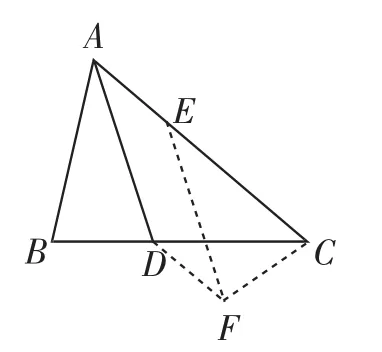
图7
分析3:根据对称性结合法3,我们能否在AC上截取CE=AB,然后证明AE=BD?
法4:在AC上截取CE=AB,然后过D作DF∥AE且DF= AE,连接EF、FC,再证明BD=AE(如图7).
第二类:补短法(共六种方法).
分析4:我们可以猜测,截长与补短在地位上、功能上是一样的,据此,我们展开补短法的探究.
法5:延长AB到E,使BE=BD,连接DE,然后证明AE= AC(如图8).
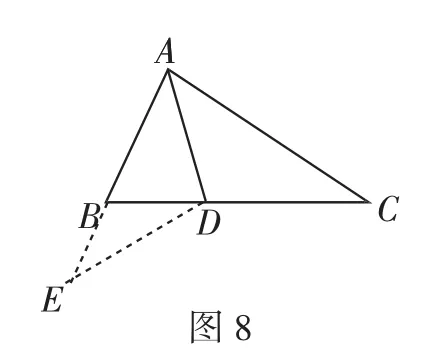
图8
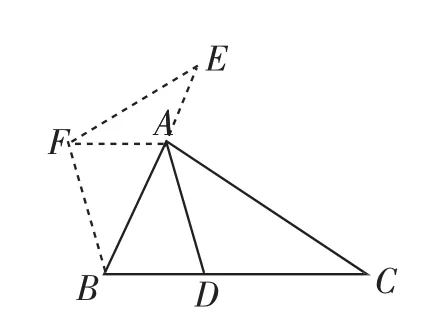
图9
分析5:法5中,我们是延长AB到E,根据对称性,我们能否延长BA到E,使AE=BD,然后证明BE=AC?
法6:延长BA到E,使AE=BD,然后过B点作BF∥AD 且BF=AD,连接AF、EF,然后证明BE=AC(如图9).
分析6:法6是过B点作BF∥AD且BF=AD,根据对称性,我们能否在线段BE的另一个端点E作辅助线呢?
法7:延长BA到E,使AE=BD,然后过E点作EF∥AD 且EF=AD,连接BF、DF,然后证明BE=AC(如图10).(需要说明的是F点可能在线段AC上,也可能在线段AC的上方或下方,这并不影响证明的可行性)
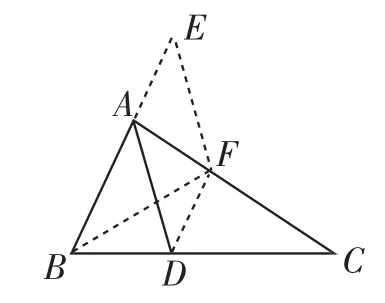
图10

图11
分析7:法5是延长线段AB,法6、法7是延长线段BA,我们能否延长线段DB呢?
法8:延长DB到E,使BE=AB,连接AE,然后证明DE= AC(如图11).
分析8:法8中,是从线段BD的B点向左延长,我们能否从线段BD的D点向右延长呢?
法9:延长BD到E,使DE=AB(实际上是截取),然后过E点作EF∥AD且EF=AD,连接BF、AF,最后证明BE= AC(如图12).(需要说明的是E点可能与C点重合,也可能在点C的左边或右边,这并不影响证明的可行性)
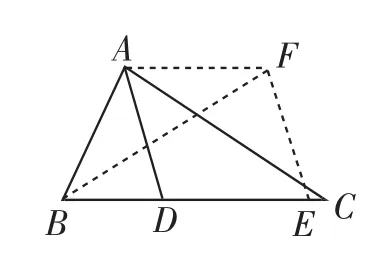
图12
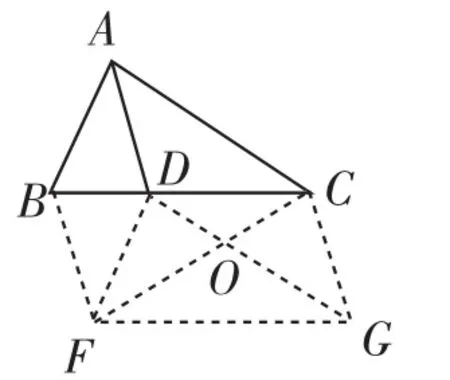
图13
分析9:法9中,是在线段BC的上方作辅助线,我们能否在线段BC的下方作辅助线呢?
法10:延长BD到E,使DE=AB(实际上是截取),然后过B点作BF∥AD且BF=AD,过C点作CG∥BF且CG=BF,连接FD、DG、EF、FG,DG、EF相交于点O,最后证明BE= AC(如图13).(需要说明的是E点可能与C点重合,也可能在点C的左边或右边,这并不影响证明的可行性)
第三类:从角出发(共有四种方法).
观察前面的10种解法,都是首先基于线段长度的思考,我们知道线段的长和角是度量图形数量关系的两种根据,从广义的角度来看,这两种度量关系也是对称的,如果我们从角的角度来看,会有什么样的解法呢?
法11:作∠ABC的平分线BE,交AD于点E,然后作DF∥BE交AB的延长线于点F(如图14),然后证明△AFD≌△ACD.实际上,这种方法和法5有异曲同工之妙.
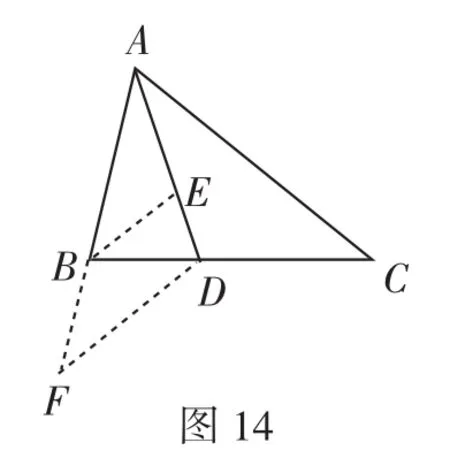
图14
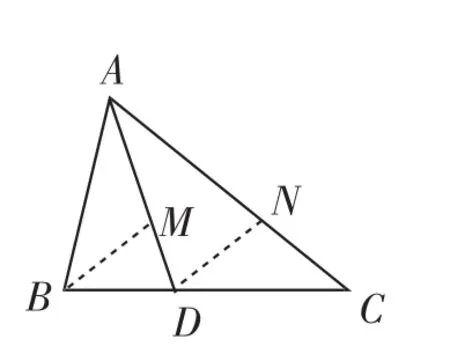
图15
分析10:法11中,是过D点作DF∥BE交AB的延长线于点F,那么能否过D点作DN∥BM交AC于点N呢?
法12:作∠ABC的平分线BM,交AD于点M,然后作DN∥BM交AC于点N(如图15),然后证明△ABD≌△AND.实际上,这种方法和法1、法3有异曲同工之妙.
分析11:法11、法12是针对∠ABC设计的辅助线,分析重要的已知条件∠B=2∠C,从对称性的角度思考,我们能否针对∠C设计辅助线解题呢?
法13:作∠ADE=∠ADB,交AC于点E,然后证明△ABD≌△AED(如图6).(与法3有异曲同工之妙)
法14:作∠CDE=∠C,交AC于点E,然后证明△ABD≌△AED(如图6)(与法3有异曲同工之妙)
三、基于对称视角的一题多法的再思考
由于版面所限,本文只能选取5个例题说明对称思想指导下的一题多法的研究,根据上述例题的简略步骤,我们有如下的思考.
1.根据对称的思想找到添加辅助线的方法,但是解法之间的繁简程度上是不对称的
对于几何题目,特别是例5,虽然我们找出了14种方法,而且全部能解,但是根据添加辅助线的繁杂程度我们可以揣测解题步骤的繁简程度,比较简单、常用的是法1、法3、法5、法8、法13、法14,其余都比较复杂.虽然我们能够根据对称的思想找到添加辅助线的方法,但是我们发现它们在解题的繁简程度上是不对称的!笔者认为比较简单的解法往往吻合几何中条件集中的原则,比较复杂的解法常常是割裂了已知条件之间的内在关联.
我们可以借助于算法框图展示一题多法形成的思维过程:
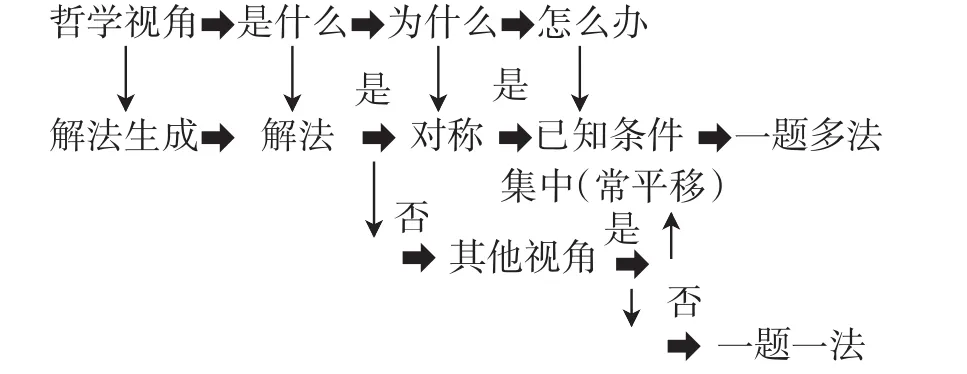
2.对称是集知识结构、认知结构、思维结构和智能结构为一体的综合成因
对称性的视角是开启学生解题思路之门的钥匙,它能够引导学生养成多层次、多角度思考问题的习惯;全面地应用知识来分析问题、解决问题;培养学生思维的灵活性、发散性、应变性和全面性.
在解决数学问题的过程中,不要奢望任意选择一种方法都能解决问题,当解题遇到困难时,应该快速联想到其他解题思路,从而避免思路误入死胡同.
3.初生之物其形必丑,臻善臻美需同仁助力
本文涉及几何和方程等两类比较常见、简单、典型的例题,由于版面关系,删掉了一个代数求值的问题,而对称理论广泛应用还需要读者在深入的基础上进一步体验.
本文的研究是抛砖引玉的探索行为,就其成果而言是一个粗糙的、前瞻性的、成长中的理论,还有很多不完善的地方,比如,条件之间的对称性的界定,对称性的普适性的研究等.这个理论还需要我们在解题实践中不断地细化、完善、发展.
参考文献:
1.孙琪斌.从一个有趣的证法成对说起[N].上海中学生报(中招周刊),2009-10-20(11).
2.孙琪斌.再谈“证法成对出现”[N].上海中学生报(中招周刊),2010-11-22(11).
3.慕学忠,王志进.探索布列方程通法的拾级历程[J].中学数学教学参考(中),2011(4).
4.陈宏亮.从“学不得法”谈从条件寻找思维起点——从一份七年级考卷的两道题说起[J].中学数学(下),2015(3).
5.曹伟娟.从一题多解到多解归一:解题教学的一种追求——2015年湖北武汉卷第24题解析与反思[J].中学数学(下),2015(10).
