基于增益调度的变速控制力矩陀螺操纵律设计*

张科备，王大轶，汤亮

(1.北京控制工程研究所，北京100190;2.空间智能控制技术国防重点实验室，北京100190)

基于增益调度的变速控制力矩陀螺操纵律设计*

张科备1，2，王大轶1，2，汤亮1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术国防重点实验室，北京100190)

针对以往变速控制力矩陀螺(VSCMGs)加权操纵律存在增益调度与卫星姿态机动信息脱节的不足，设计一种VSCMGs改进增益调度操纵律.不同于以往VSCMGs加权操纵律仅通过奇异度进行增益调度，改进型操纵律采用奇异度结合误差四元数进行增益调度设计，能够根据卫星姿态机动信息进行增益调度，同时该操纵律通过添加零运动，实现规划CMGs框架角和转子转速收敛在标称值附近，避免转子转速饱和.仿真结果表明改进增益调度操纵律能够实现CMGs模式和RWs模式二者之间平滑切换，有利于实现大力矩输出和精细力矩输出.

增益调度;VSCMGs;操纵律;姿态机动

0 引言

在未来航天事业发展中，越来越多的航天任务要求航天器具有姿态快速机动和快速稳定的能力.控制力矩陀螺(control moment gyros，CMGs)作为一种新型的执行机构，具有大力矩输出特点，使得CMGs广泛应用于大型航天器平台［1］.然而，当处于奇异状态时，CMGs不能输出三维任意方向的力矩.针对此问题，工程人员引入了变速控制力矩陀螺(variable-speed control moment gyros，VSCMGs)，采用其反作用轮(reaction wheels，RWs)模式输出力矩进行CMGs避奇异.与CMGs相比，VSCMGs具有额外的控制自由度.它可以通过改变转子转速输出力矩，进行奇异状态规避.理论上，VSCMGs能够实现输出三维任意方向的力矩，但是在实际中仍需要驱动框架角远离奇异状态，才能更有效地实现CMGs力矩放大能力.VSCMGs既可以采用CMGs模式输出大力矩，也可以采用RWs模式输出精细力矩，或者同时采用以上两种模式输出力矩.因此，VSCMGs作为高效能的执行机构在高精度指向和高稳定度的敏捷卫星中发挥着不可替代的作用［2-3］.

针对VSCMGs，许多学者设计了多种操纵律进行避奇异和力矩输出规划.Yoon和Leeghim等［4-6］在分析VSCMGs奇异度的基础上设计了一种刻度因子进行VSCMGs转子转速的描述，针对不同的任务需求来设计调节刻度因子进行VSCMGs最佳角动量的设置.Lee等［7-8］将上述一步预测奇异度的操纵律应用到VSCMGs中，通过最小化奇异指标和能量的指标函数，得到了VSCMGs的最优操纵律.分析证实，基于一步奇异预测的VSCMGs操纵律与添加零运动的最优解操纵律是等价操作，但是基于奇异度量预测的操纵律能够处理VSCMGs转子转速饱和现象.为了减小控制关联矩阵的条件数，进行性能良好的避奇异，Schaub等［9-10］设计了VSCMGs的带零运动操纵律.在VSCMGs加权操纵律的基础上添加零运动，能够提高避奇异性能.Mcmahon等［11］采用一种简单的方法将CMGs操纵律的零运动添加到VSCMGs加权操纵律中.该方法不是通过跟踪计算VSCMGs操纵律投影矩阵的秩来设计避奇异，而是基于跟踪旋转轴的范围进行计算，且不需要通过获取转子转速来设计避奇异零运动，极大的简化了零运动的计算.杨雅萍等［12］针对VSCMGs设计了增益调度型的操纵律，但是该操纵律不能根据姿态信息进行CMGs模式和RWs模式之间转化.在姿态稳定控制时，控制精度低.Shinya等［13］将误差四元数矢量模引入操纵律中，设计了根据误差四元数的增益调度操纵律.但是该操纵律没有进行良好的零运动规划，仿真校验该操纵律发现该操纵律不能通过双曲奇异点.

文中重新审视了由Schaub等提出的带零运动操纵律以及杨雅萍和Shinya等提出的增益调度变速控制力矩陀螺操纵律，发现以往的增益调度操纵律往往是在远离奇异时采用CMGs模式，当接近奇异状态时采用RWs模式进行避奇异.这样的操纵律没有对CMGs模式和RWs模式的系数进行灵活规划，不利于卫星本体的高精度稳态控制.同时，也没有很好的对RWs的转速进行规划，采用操纵律在控制VSCMGs多次接近奇异状态后，容易出现RWs转子转速饱和现象，从而影响控制力矩陀螺避奇异性能和姿态稳定性能.而RWs转子转速饱和现象往往是工程实践中需要解决的问题，因此需要对增益调度操纵律进行改进，在原来的基础上添加零运动和转子转速平衡项，使RWs在标称转速附近工作，避免转速饱和.

1 问题描述

1.1 问题提出

在实际卫星姿态机动中，需要多个VSCMGs进行三维力矩输出.常用的VSCMGs构型有双平行结构、屋顶型结构、金字塔结构.其中在金字塔形结构下，VSCMGs的角动量轮廓接近球状，有利于三维力矩的输出.因此成为最常用的构型.金字塔构型示意图如图1所示，其框架倾斜角为β，在经典金字塔构型下，β=53.13°.在初始状态下，各个VSCMGs的角动量在XY平面内.

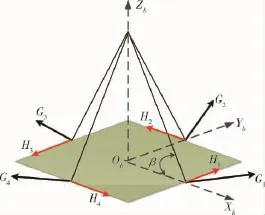
图1 VSCMGs金字塔构型Fig.1Pyramid configuration for VSCMGs

在金字塔构型下VSCMGs的动力学方程为

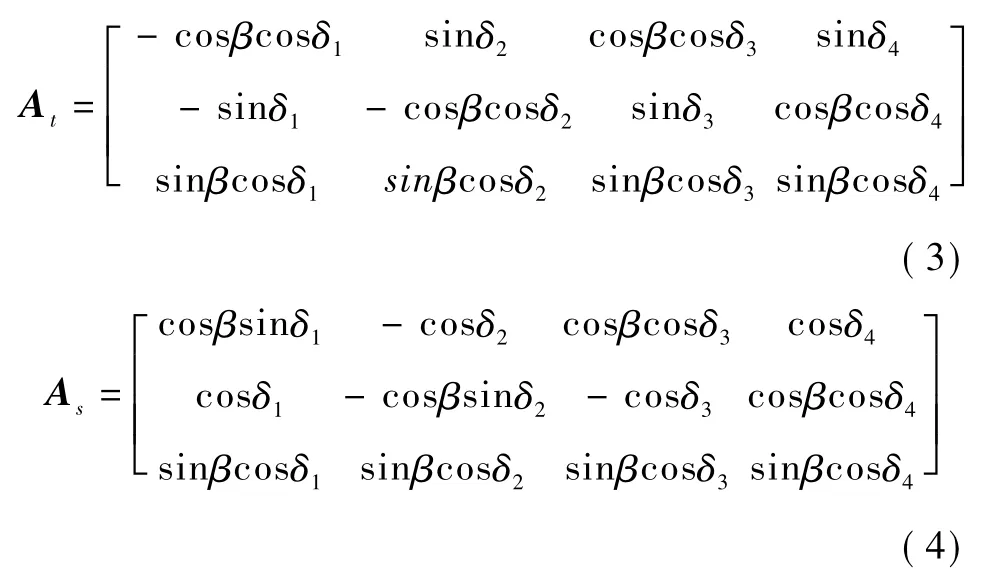
常用的VSCMGs操纵律为加权操纵律，通过分配CMGs和RWs之间权重系数，进行VSCMGs操纵.其加权操纵律为

式(5)中，CMGs权重系数Wgi和RWs权重系数Wsi一经设定好后，CMGs模式的输出力矩与RWs模式输出力矩之比固定，不能根据姿态机动信息进行合理的调节二者之间的比重.因此，需要在上述加权操纵律的基础上，进行改进增益调度的操纵律研究，优化VSCMGs的输出力矩.

1.2 姿态控制基本知识

带n个VSCMGs的刚体卫星动力学方程为

设计的PD控制器为

式中，Kp、Kd为控制器增益为误差四元数的矢量部分，Δω为期望角速度ωr与测量角速度ω之差.

2 改进增益调度操纵律

2.1 增益调度设计

VSCMGs主要的工作模式有3种:CMGs模式，进行大力矩输出;RWs模式，进行精细力矩输出; VSCMGs混合模式，即CMGs模式和RWs模式同时工作.在卫星姿态机动过程中，我们希望采用VSCMGs模式或CMGs模式.卫星进行姿态稳定控制时，应采用RWs模式.此时需要VSCMGs进行框架角锁死或接近锁死状态，避免VSCMGs框架角晃动带来误差干扰力矩.

文献［13］设计了局部梯度增益调度的避奇异，该操纵律中只给框架角添加零运动，没有针对RWs转子转速进行平衡规划.在实际姿态控制中，由于存在转子摩擦力矩，在没有对RWs转子转速进行转速平衡规划的情况下，RWs的转子转速或出现一直下降的趋势，这直接降低了VSCMGs的角动量，对姿态机动造成不利影响.针对这种情况，对式(5)中的权重系数进行增益调度设计

式中，

2.2 零运动避奇异

文献［12-13］在设计VSCMGs操纵律时，只添加了框架角的零运动，没有对RWs转子转速添加零运动，从而实现零运动避奇异和转子转速保持.在文献［14-15］中设计了一种VSCMGs转子零运动避奇异和转子转速平衡算法.该算法采用零运动投影矩阵，进行VSCMGs避奇异和转子转速保持.其VSCMGs零运动操纵律具体表达式为

式中，kN1为设计参数，P=(I8×8－WQT(QWQT)－1)为零运动正交投影矩阵，I8×8为8维单位矩阵，δf为期望框架角，Ωf为期望转子转速.零运动操纵律并不额外输出力矩，但是零运动操纵律通过计算当前框架角和转子转速与期望框架角和期望转子转速之间误差，驱动VSCMGs向着期望值运动，从而使VSCMGs远离奇异点.在零运动避奇异方面采用文献［14］中提出的基于VSCMGs雅克比矩阵奇异值分解的方法进行零运动避奇异

式中，kc为设计参数，K2为雅克比矩阵At条件数倒数.

式(13)中的零运动操纵律存在以下不足:由于投影矩阵P的作用，当VSCMGs接近奇异状态时不能驱动VSCMGs快速脱离奇异状态.由于VSCMGs低速框架和高速转子都可以输出力矩.因此，当VSCMGs接近奇异状态时充分利用=0这一特点进行零运动操纵律设计，使VSCMGs快速远离奇异点.具体的零运动操纵律为

式中:kN2为零运动xN2的权重系数

文献［14］将式(14)中kc设为一固定的值，其合理之处在于限制零运动的幅值，预防VSCMGs的输出力矩饱和.但是，当VSCMGs接近奇异时，由于上式中的kc限制，添加的零运动幅值较小，不能使VSCMGs迅速脱离奇异状态.针对此不足，对零运动的增益调度设计为

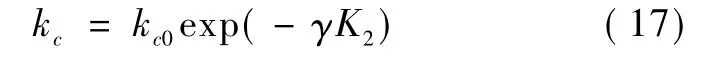
式中，kc0，γ为设计参数.

在增益调度操纵律计算得到的指令框架角速度和转子转速变化率的基础上添加上述零运动操纵律，进行避奇异和转子转速平衡.则文中设计的了的操纵律为

3 仿真校验

在刚体卫星姿态机动过程中，常用的路径规划方法有BCB、五次多项式、抛物线等路径规划方法.本文采用五次多项式路径规划进行卫星大角度机动，分别在初始框架角为最优框架角和奇异状态两种情况下校验所提出的增益调度操纵律.仿真的参数如表1所示.

表1 仿真参数Tab.1Parameter for simulation

Case 1:快速远离奇异点数学仿真验证

按表1中的参数进行卫星姿态机动仿真，设置初始框架角为:δ(0)=［900－900］°，机动过程中VSCMGs的奇异度如图2所示.在机动初始时刻，VSCMGs处于奇异状态，此时零运动操纵律一方面通过提高零运动系数(如图3所示)进行VSCMGs快速远离奇异点;另一方面，VSCMGs直接朝着奇异度最大的框架角组合δf运动，其产生的额外力矩通过VSCMGs的转子进行补偿，从而使VSCMGs快速远离奇异状态.如图4所示在初始时刻，VSCMGs处于接近奇异状态，此时采用RWs模式进行力矩输出，转子以最大力矩输出，当VSCMGs远离奇异状态时，VSCMGs采用CMGs模式和RWs模式共同工作.

图2 VSCMGs奇异度Fig.2VSCMGs singularity

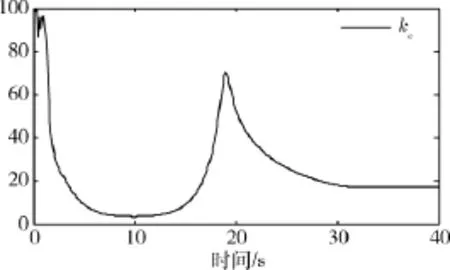
图3 零运动系数Fig.3Coefficient for null motion

图4 RWs输出力矩Fig.4Torque generated by RWs

Case 2:姿态稳定实验

在三轴气浮台上，按表1中的参数进行多次姿态机动物理仿真实验.设置VSCMGs的初始框架角为:δ(0)=［4522545225］°.在机动实验中分别对比VSCMGs力矩分配系数为固定值和采用式(11)进行VSCMGs力矩分配系数增益调度设计两种情况下的姿态稳定度.由于VSCMGs克服摩擦运动以及零运动操纵律驱动框架和转子运动，这些运动往往对星体产生一定的干扰力矩，从而造成星体的姿态波动，直接影响控制精度.图5显示两种分配系数情况下，姿态稳定情况，姿态稳定情况，在2 950～3 050 s设置一组分配进行卫星姿态稳定度观测，在3 050～3 150 s设置另一组分配系数进行卫星姿态稳定度观测，从而证明在稳定控制与姿态机动两种模式下需要设置良好的增益调度系数，提高姿态稳定度.图6为采用增益调度力矩分配系数下姿态控制稳定度.通过图5和图6对比，说明了通过增益规划，在姿态稳定控制时能够降低CMGs模式系数从而减小对星体的扰动力矩，提高姿态稳态度.在姿态机动过程增大CMGs模式系数以满足大力矩输出要求，实现星体的敏捷机动.图7为在多次姿态往返姿态机动试验中VSCMGs奇异度量K1、K2.从而证明所设计的操纵律能够正确驱动VSCMGs朝着远离奇异状态的方向运动，证明设计的操纵律的正确性.

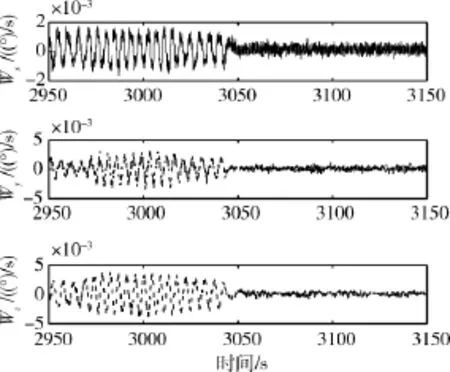
图5 不同力矩分配系数时姿态稳定度Fig.5Attitude stability for different torque coefficient

图6 增益调度力矩分配系数时姿态稳定度Fig.6Attitude stability for gain scheduled torque coefficient

图7 增益调度力矩分配系数时VSCMGs奇异度Fig.7VSCMGs singularity for gain scheduled torque coefficient

4 结论

文中设计改进型增益调度操纵律，所设计的操纵律由指令运动和零运动两部分组成.在指令运动中，进行CMGs模式和RWs模型增益调度.通过判读姿态误差四元数进行合理调节CMGs模式和RWs模式系数，使VSCMGs输出期望力矩.在姿态机动时主要以CMGs模式为主，在姿态稳态控制时，主要以RWs为主.文中分别在两种情况下(一种为奇异值最大，一种为奇异度为0)，进行卫星大角度机动.仿真结果表明，改进增益调度操纵律能够通过VSCMGs的奇异状态，在大角度机动时主要采用CMGs模式进行大力矩输出，在姿态机动结束后能够调节CMGs模式系数趋于0，进行CMGs锁死，以RWs模式为主要输出力矩模式，进行卫星高精度稳态控制.

［1］GURRISI C，SEIDEL R，DICKERSON S.Space station control moment gyroscope lessons learned［C］//Proceedings of the 40thAerospace Mechanisms Symposium.FL:SEE，2010.

［2］ZHANG H J，FANG J C.Robust backstepping control for agile satellite using double-gimbal variable-speed control moment gyroscope［J］.Journal of Guidance Control，and Dynamics，2013，36(5):1356-1363.

［3］WIE B，BAILEY D，HEIBERG C.Rapid multi-target acquisition and pointing control of agile spacecraft［J］.Journal of Guidance Control，and Dynamics，2002，25 (1):96-104.

［4］YOON H，TSIOTRAS P.Singularity analysis of variable-speed control moment gyros［J］.Journal of Guidance Control and Dynamics，2004，27(3):374-386.

［5］LEEGHIM H，BANG H，PARK J O.Singularity avoidance of control moment gyros by one-step ahead Singularity Index［J］.Acta Astronautica，2009，64(9): 935-945.

［6］LEEGHIM H，LEE I H，LEE D H.Sigularity avoidance of control moment gyros by predicted singulairty robustness:ground experiment［J］.IEEE Transactions on Control Systems Technology，2009，17(4):884-891.

［7］LEE H，LEE I H.Optimal steering laws for variable speed control moment gyros［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Washington D.C.:AIAA，2005.

［8］LEE H，BANG H.Singularity avoidance of variable speed control moment gyros by optimization approach［J］.Journal of the Astronautical Sciences，2007，55 (1):67-84.

［9］SCHAUB H，JUNKINS J L.Singularity avoidance using null motion and variable-speed control moment gyros［J］.Journal of Guidance Control and Dynamics，2000，23(1):11-16.

［10］SCHAUB H，VADALI S R，JUNKINS J L.Feedback control law for variable speed control moment gyros［J］.Journal of the Astronautical Science，1998，(46):307-328.

［11］MCMAHON J，SCHAUB H.Simplified singularity avoidance using variable-speed control moment gyroscope null motion［J］.Journal of Guidance，Control，and Dynamic，2009，32(6):1938-1943.

［12］杨雅萍，吴忠.变速控制力矩陀螺模式调度型操纵律设计［J］.空间控制技术与应用，2011，37(3):9-13.YANG Y P，WU Z.Mode-scheduling steering law design for variable speed control moment gyroscope［J］.Aerospace Contrd and Application，2011，37(3):9-13.

［13］SHINYA K，HIROHISA K.Gain-scheduled steering control law for variable speed control moment gyros［C］//AIAA Guidance，Navigation，and Control Conference.Washington D.C.:AIAA，2013.

［14］汤亮.使用控制力矩陀螺的航天器姿态动力学与控制问题研究［D］.北京航空航天大学，2005:1-15.

［15］邢林峰，孙承启，汤亮.高姿态稳定度敏捷卫星的VSCMGs操纵律研究［J］.空间控制技术与应用，2008，34(6):24-28.XING L F，SUN C Q，TANG L.VSCMGs-based steering law design for a high attitude stability agile satellite［J］.Aerospace Contrd and Application，2008，34(6):24-28.

Steering Law for Attitude Control with Variable-Speed Control Moment Gyros Based on Gain-Scheduled

ZHANG Kebei1，WANG Dayi1，2，TANG Liang1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

A modified singular avoidance steering law for variable-speed control moment gyros(VSCMGs)is proposed in this paper.Contrary to the traditional weighted steering law that uses singular measure in reaction wheels(RWs)mode for singularity avoidance，the modified steering law uses both the singular measure and error quaternion for gain schedule and singularity avoidance，the modified steering law decreases the CMGs mode coefficients and increases the RW mode coefficients to generate precise torque.The null motion is added to steer the gimbal angle and rotation speed approaching to the nominal value.Numerical simulations demonstrate the effectiveness of the modified gain scheduled steering law.

gain-scheduled;VSCMGs;steering law; attitude maneuver

V448.2

A

1674-1579(2016)06-0031-06

10.3969/j.issn.1674-1579.2016.06.006

张科备(1985—)，男，博士研究生，研究方向为航天器精确指向和高稳定控制.王大轶(1973—)，男，研究员，研究方向为深空探测航天器自主控制.汤亮(1973—)，男，研究员，研究方向为航天器动力学与控制.

*国家杰出青年科学基金资助项目(61525301).

2016-05-18