双层智能优化算法求解时变网络最短路径问题

2016-04-13卢厚清

装备学院学报 2016年1期

关键词：最短路径

陈　亮，　卢厚清

(1.解放军蚌埠汽车士官学校运输勤务系, 安徽蚌埠 233011；　2.解放军理工大学野战工程学院, 江苏南京 210007 )

双层智能优化算法求解时变网络最短路径问题

陈亮1，卢厚清2

(1.解放军蚌埠汽车士官学校运输勤务系, 安徽蚌埠 233011；2.解放军理工大学野战工程学院, 江苏南京 210007 )

摘要边成本为一般函数的时变网络最短路径问题(TDSP)，已被证明不存在多项式时间算法。同时智能优化算法被广泛地用于求解该类问题，但多数没有考虑节点的可等待约束。提出了求解TDSP问题的双层智能优化算法，内层遗传算法优化每条可行路径的各节点离开时间，外层蚁群算法优化构建的路径，最终搜索到从起始点到终点的最短时间路径。实验结果表明：双层智能优化算法能快速寻优，并且收敛速度和最优路径较同类算法更优秀。

关键词时变网络；最短路径；双层优化；智能优化算法

Time-dependent Shortest Path Problem in Solution to Two-level Intelligent Optimization Algorithm

CHEN Liang1,LU Houqing2

(1. Department of Transportation Service, Bengbu Automobile NCO Academy, Bengbu Anhui 233011, China；2. College of Field Engineering, PLA Univ.of Sci.& Tech.Nanjing Jiangsu 210007, China)

AbstractIt is proven there is no polynomial time algorithm for the time-dependent shortest path (TDSP) occurring when marginal cost is a general function. Also, intelligent optimization algorithms are extensively used in solving such problems, but most of them have not considered the waiting constraint of the nodes. This paper brings out the two-layer intelligent optimization to solve out TDSP problem: at internal layer, optimize the leaving time of each node of each feasible path with genetic algorithm; at external layer, optimize the built path with ant colony algorithm. In this way, the shortest time path from a starting point to an end point is obtained. The experimental result shows, the two-level intelligent optimization algorithm is able to identify the optimization and the convergence speed with optimized path is better than other algorithms.

Keywordstime-dependent networks; shortest path problem; two-layer optimization; intelligent optimization algorithm

在战时配送运输过程中，选择到达时间最短的路径，可以达到快速开进、降低损耗的目的。但是，战时组织军事配送运输，由于战场环境的恶劣、多变、复杂，以及敌人的袭击破坏，使得军事配送运输网络的边权(如配送距离、时间等)具有动态可变性，相对于边权不发生变化的静态网络，这类网络被称为动态网络。动态网络按照边权的特性，又可分为随机网络(Stochastic Network，SN)、模糊网络(Fuzzy network，FN)和时变网络(Time-Dependent Network，TDN)，SN中的边权是随机变量，FN中边权是模糊不定的，而TDN中的边权表现为时间的函数，本文主要研究时变网络最短路径(Time-Dependent Shortest Path，TDSP)问题。

对于TDSP问题，学者做了大量工作。文献[1]首次指出传统的最短路径算法不适用于时变网络最短路径问题，须建立严格的一致性约束条件才能求解。文献[2]将TDN分为FIFO(First-in First-out)网络和非FIFO网络两类，证明可用Dijkstra算法求解FIFO网络的TDSP问题；在假定时间离散状态下，给出了一种利用逆序动态规划思路求解的非FIFO网络的TDSP方法。文献[3]在研究时变网络模型和理论的基础上，给出了最短时间路径的充要条件，提出了一种可同时适合FIFO网络和非FIFO网络的最短路径算法。文献[4]提出了等待时域和最佳出发时间理论，给出了一种求解TDSP问题的改进Dijkstra算法。但这些算法对时间是有要求的，要么是离散的，要么需对时间进行离散化处理。因此，算法的时间效率不高，针对这些问题，文献[5]用基因插入和基因删除对单亲遗传算法进行了改进，并用于求解TDSP问题，取得了不错效果。文献[6]将遗传算法和蚁群算法相结合，对蚁群算法构建的路径进行单点交叉，有效避免算法陷入停滞，提高了算法收敛效率。文献[7]提出了一种改进的蚁群算法，将交通流密度因子引入到信息素更新策略中，并对蚁群算法构建的路径进行交叉处理，新算法能有效解决时间交通系统中的最短路径问题。

但这些算法均未考虑节点的可等待约束，在军事配送运输过程中，由于道路破坏、阻塞，车辆的运输时间是依时间变化的，即路阻函数是时间的函数。运输车辆在某个节点做适当停留是允许的，并且很可能是必要的。因此研究节点可等待约束的TDSP对于战时配送运输具有重要的指导和现实意义。

本文考虑节点等待约束的情况下，分层次优化TDSP问题，内层采用遗传算法优化每条可行路径各节点离开时间，得到某条路径的最短时间路径；外层采用蚁群系统算法优化路径本身，最终得到最优路径方案。

1蚁群系统算法

蚁群系统算法是一种模拟蚂蚁群体智能行为的群智能优化算法，它具有优良的分布式计算机制、鲁棒性等优点，并且易于与其他优化方法相结合。为了说明蚁群系统算法，首先介绍旅行商问题(Traveling Salesman Problem, TSP)。

1.1旅行商问题

一般的，TSP问题可描述如下[8]：G={N,A}是一个带权完全图，其中N={1,2,…n}是n个城市的集合，A={(i,j)|i,j∈N}是所有边的集合。每一条边(i,j)∈A都分配一个权值dij，代表城市i与城市j之间的距离，其中i,j∈N。TSP的目标是寻找图中一条长度最短的哈密尔顿回路，即找出对N={1,2,…n}中n个城市访问且只访问一次的最短的一条封闭路径。TSP问题可分为对称型和非对称型，在对称TSP中，集合A的所有边均满足dij=dji；在非对称TSP中，至少存在一条边(i,j)，使得dij≠dji。

1.2蚁群系统算法

蚁群系统算法(Ant Colony System,ACS)是基于蚂蚁系统(Ant System,AS)的改进算法，其性能比AS有明显的提高。改进部分体现在3个方面：

第一，位于城市i的蚂蚁k，根据伪随机比例规则选择城市j作为下一个访问的城市。该规则由下式给出

(1)

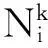
第二，信息素的释放动作只在至今最优路径的边上执行。更新信息素方式如下：

(2)

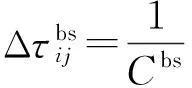
第三，蚂蚁在构建路径时，每一次使用边(i,j)，就会从该边去掉一定量的信息素

(3)

式中，ε满足0<ε<1;τ0是信息素量的初始值。改进后的局部信息素更新方式，使得蚂蚁每经过边(i,j)，该边的信息素量τij将会减少，从而使得后续蚂蚁选择该边的概率降低。也就是说，可以增加蚂蚁探索其余路径的可能性，增强算法开发的广度，使得算法不陷入停滞状态。同时，局部更新方式使得更新后的信息素量将在初始信息素量τ0和旧的信息素量之间，保证了该边在下一次构建路径时仍然可能被选中。

2时变网络数学模型

定义1[9]43G={V,E,F(t)}，其中V={1,2,…n}是有限节点集合，E={(i,j)|i≠j,i,j∈V}是边的集合，F(t)={fij(t)|(i,j)∈E}为边权函数的集合，其中fij(t)是时间t的函数，t∈[a,b],b>a≥0，则称G为时变网络TDN。a是所有结点的最早的允许出发时间，b是所有节点的最晚允许到达时间。

定义2[9]44在TDN中，设PS,D(a)表示从节点vS在a时刻出发到达节点vD的路径，即：

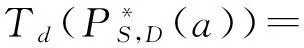
为了方便表述，取起始节点vS为1，目标节点vD为D。定义下列决策变量与符号：xij，0-1变量，取0表示边(i,j)不在vS至vD的路径中，取1表示边(i,j)在vS至vD的路径中；ai,表示当P1,n(a)给定时，到达点i的时刻；bi，表示节点i的允许等待的最大时间；li，表示当P1,n(a)给定时，离开点i的时刻。则TDSP问题的优化数学模型如下：

min(Z(x,t))=

(4)

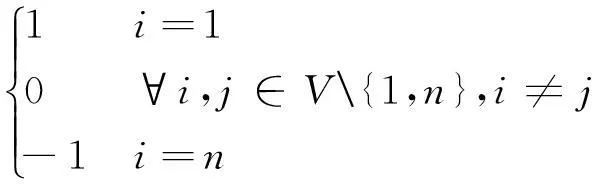
(5)

(6)

(7)

模型中：式(4)为目标函数Z(·)；式(5)为1至n路径合法性约束；式(6)为节点离开时间约束；式(7)为从1至n路径中，节点i的到达时间约束。其中，a为节点1最早允许出发时刻。

3双层智能优化算法

模型中有2组变量xi,j和li需要优化，因此本文采用分层的思想，外层利用蚁群系统算法优化变量xi,j，构建一条从起始节点1到目标节点n的路径；内层利用遗传算法优化路径中每个节点的最佳出发时间li，从而找到最短时路径。

3.1ACS算法构建路径

ACS算法优化路径步骤如下：

1) 按如下公式初始化每条边上的信息素量

式中，n表示为节点规模；Cnn是任意一条从起始点1到终点D的路径的时间长度。同时设置算法迭代次数。

2) 将m只蚂蚁放在起始点1。

3) 根据式(1)选择下一个访问节点j，启发式信息ηij=1/fij(li)，fij(li)为蚂蚁在li时刻由节点i到节点j所经历的时间。按照式(3)更新该边上的信息素。

5) 当m只蚂蚁构建完路径后，按照式(2)更新至今最优路径上的信息素。

6) 达到了给定的迭代次数，则停止；否则转步骤2)。

3.2遗传算法优化内层函数

内层函数需优化节点i的最优离开时刻li，使得对应路径的走行时间最短。依据内层函数的优化目标和约束条件，可建立以下优化模型[10]33：

(8)

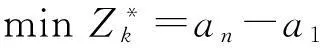
假设已得到一条路径P1,n(a)={1,2,3,…n}，显然，l1∈[a1,a1+b1]，令l1=y1，则必有l2∈[a2,a2+b2]，其中a2=y1+f1,2(y1)。

同理可推得l3∈[a3,a3+b3]，其中,a3=y2+f2,3(y2)……

因此，可设计内层遗传算法[10]33-34：

1) 编码及初始化种群。生产均匀随机变量y1∈[a1,a1+b1]，令l1=y1，得到：a2=y1+f1,2(y1)；生产均匀随机变量y2∈[a2,a2+b2]，令l2=y2，得到：a3=y2+f2,3(y2)……

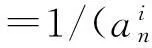
3) 选择操作。根据每条路径的适应度fit(i)，采用轮盘赌的方式从父代染色体中选择nSize个染色体作为子代。

4) 交叉操作。按交叉概率Pc选定要进行交叉操作的染色体，并依适应度大小降序排列，按照首尾对折的方法选择2个染色体进行交叉操作。假定染色体l1和l2被选中，随机均匀生成整数i∈[1,m)，m表示路径P1,n(a)包含的节点数，i表示交叉位置。交换l1和l2中第i个基因位，分别检查l1和l2的可行性，并进行修补操作。

(1) 若li满足：ai≤li≤ai+bi，i∈V，则转步骤(2)；否则转步骤(4)；

(2) 若i=m，则转到步骤(5)，否则i=i+1，计算ai=li-1+fi-1,i(li-1)；

(3) 若li满足：ai≤li≤ai+bi，i∈V，则转步骤(5)；

(4) 生成随机变量y∈[ai,ai+bi]，令li=y，转步骤(2)；

(5) 染色体可行，停止操作。

5) 变异操作。按交叉概率Pm确定出需要进行变异操作的染色体，生成均匀随机整数i∈[1,m]，i表示变异位。

(1) 生成随机变量y∈[ai,ai+bi]，令li=y。

(2) 若i=m，则转步骤(4)；否则检查染色体的可行性，i=i+1，计算：ai=li-1+fi-1,i(li)。

(3) 若li满足：ai≤li≤ai+bi，i∈V，则转步骤(4)；否则转步骤(1)；

(4) 染色体可行，停止操作。

3.3双层智能优化算法

将外层优化路径的蚁群系统算法和内层优化节点离开时间的遗传算法结合起来，可形成求解TDSP的双层智能优化算法。算法主要步骤如下：

1) 初始化每条边上的信息素，同时设置迭代次数。

2) 将m只蚂蚁放在起始点1。

3) 按照式(1)计算蚂蚁转移概率，并选择下一个节点j，更新该边的信息素。

(1) 随机产生nSize个染色体作为初始种群。

(2) 交叉操作。

(3) 变异操作。

(4) 计算染色体评价函数。

(5) 选择操作。

5) 当m只蚂蚁搜索完后，求得m条路径和对应路径时间长度Tk(k=1,2,…,m)，按照式(2)更新信息素。

6) 更新当前的最短时间路径和对应的最短时间。

7) 达到了给定的迭代次数，则算法停止；否则转步骤2)。

4算例分析

设某一地域有27个交通节点(如图1)，各交通节点之间的通行成本为时间的函数(见表1)。某保障分队以摩托化开进方式从驻地1出发，目的地为节点27，最早开进时间为a1=0。求保障分队的最优开进方案(路途中所耗时间最少，含节点等待时间)。

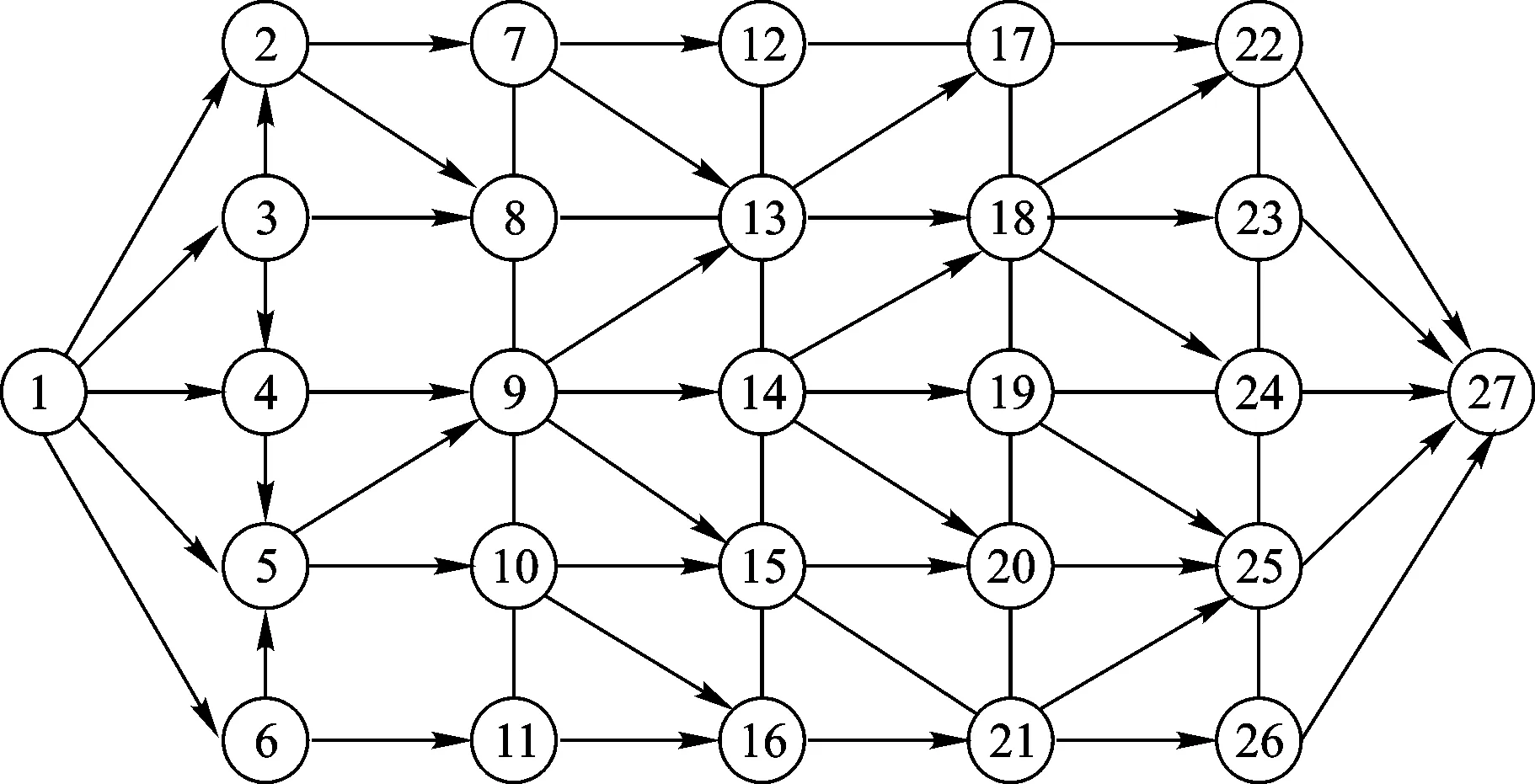
图1　时变网络示意图

顶点ibi弧fij(t)顶点ibi弧fij(t)151,21,31,41,51,63+te-t2t+3e-4t5+2e-t23+2te-3t24+(3-t)2232,72,86+(2-3t)23t+6e-t2323,23,43,82+3e-t254+(1-t/3)2434,54,96-3e-2t24505,95,103+(3-2t)22+2e-12)t2616,56,1166+(5-t)2737,127,132t+2e-t210808,78,98,1346+(7-t)211929,109,139,149,1558-2e-t29-3e-(t-2)26+(10-t)2/810310,1110,1510,163+2e-t24+(12-t)2/10611011,165+3e-2t212112,1312,1745+2e-t213213,1413,1713,1826+3e-2t27+2e-2t214114,1814,1914,203+(14-t)2/1065+3e-t15215,1415,2015,213+2e-(10-t)235-2e-3t216316,1516,218-3e-(7-t)2517117,1817,223+3e-(6-t)24-2e-t218218,2218,2318,246+3e-2t285+(18-t)2/1019219,1819,2419,259-3e-(20-t)212-3e-(16-t)210+2e-t220120,1920,2120,253+5e-2t25+2e-t23+4e-3t221221,2521,263+(20-t)2/54+(18-t)2/822222,2322,276-3e-(2+t)27+2e-t223123,2423,278+(25-t)2/66+(23-t)2/824224,2524,275+(24-t)2/64+(26-t)2/725325,2625,276+2e-3t20.18+4e-(3+t)226226,2710+3e-4(4-t)2

蚁群系统算法相关参数为：蚂蚁数为10，迭代次数为100次，α,β,ρ和ε分别取1，2，0.1和0.1。遗传算法相关参数为：种群大小为30，Pc=0.8，Pm=0.05，迭代次数为100次。实验采用Matlab 2010b编程，运行环境为：Window XP sp2，intel Core i3-2100 CPU 3.10 GHZ，DDR3 1333 MHZ 2 GB PC。

4.1双层智能优化算法优化过程

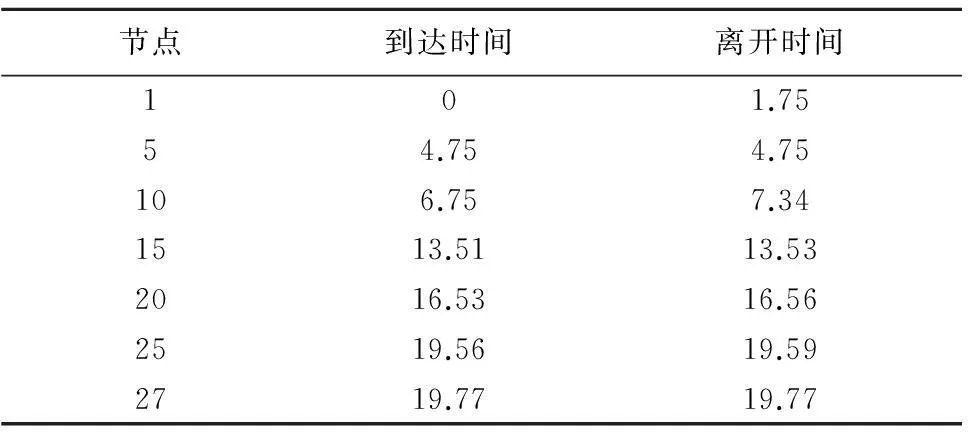
利用双层智能优化算法进行实验，最短路径的进化过程如图2所示，当迭代到87代时，问题收敛于19.77 min。当算法取得最短时路径时，的进化过程如图3所示，当迭代到56代，问题收敛。最短时路径为：1→5→10→15→20→25→27，开进方案如表2所示。

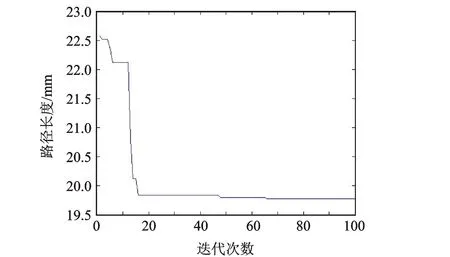
图2　最短路径进化过程

图3　最短路径时间li的进化过程

min

从最优开进方案来看，在起始点1等待1.75 min出发是最佳出发时刻，到达节点5立刻出发，在节点10等待0.59 min，在节点15等待0.02 min，在节点20等待0.03 min，在节点25等待0.03 min，最后到达终点27，总花费时间为19.77 min。与文献[10]的最优开进方案时间25.12 min相比，有较大提高。

4.2与文献[10]中算法比较

选取文献[10]33-35的双层智能优化算法(GA-GA)与本文算法(ACS-GA)做对比测试，算法分别独立运行20次，实验结果如表3所示。其中，LBest是最短时路径长度；LWorst是最长时路径长度；μ和σ分别表示运行20次得到解的平均长度和标准偏差；T为算法的平均收敛时间。

表3中的最短时路径长度、平均长度体现本文算法的收敛精度和寻优能力优于GA-GA算法；最长时路径长度、标准偏差体现了本文算法的鲁棒性和对抗局部极值的能力强于GA-GA算法；结合平均收敛时间，表明本文算法收敛效率优于GA-GA算法。

表3　2种算法总体性能的比较

5结束语

本文针对边成本为一般函数和节点存在可等待约束的TDSP问题，提出了一种双层智能优化算法。选取了包含27个节点的时变网络进行实验，实验结果表明本文算法能够快速找到最短时间路径方案。与同类算法的比较试验表明，本文算法收敛精度和寻优能力更优，鲁棒性和对抗局部极值的能力更强。在配送运输网络中，边权不仅仅是时间的函数，还可能同时是随机变量，也就是说时变网络与随机网络共同存在，求解这类问题，是下一步研究的重点内容。

参考文献(References)

[1]HALL R W.The fastest path through a network with random time dependent travel time[J].Transportation Science，1986，20(3)：182-188.

[2]谭国真，高文.时间依赖的网络中最小时间路径算法[J].计算机学报，2002，25(2)：165-172.

[3]何俊，戴浩，宋自林，等.时间依赖的交通网络模型及最短路径算法[J].解放军理工大学学报(自然科学版)，2005，6(6)：541-544.

[4]韩平阳，罗五明，王志敏，等.动态网络中的最短路径改进算法[J].军事运筹与系统工程，2007，21(1)：46-50.

[5]刘坚强，刘粉明.动态网络最佳路径的遗传算法求解[J].信息工程大学学报，2004，5(3)：14-18.

[6]刘永强，常青，熊华钢.改进蚁群算法求解时变网络中最短路径问题[J].北京航空航天大学学报，2009，35(10)，1245-1248.

[7]薛国新，王岳.一种改进的蚁群算法求解出来的最短路径问题[J].常州大学学报(自然科学版)，2012，24(1)，78-81.

[8]王学超，孔月萍，董丽丽，等.智能优化算法与应用[M].西安：西北大学出版社，2012：164-165.

[9]李引珍．不确定环境下交通运输网络路径求解方法及应用研究[D]．成都：西南交通大学，2005：43-44.

[10]何瑞春，李引珍.时间依赖网络路径模型及双层优化智能算法研究[J].铁道学报，2008，30(1)：32-37.

(编辑：李江涛)