基于载荷谱的结构疲劳寿命预测技术研究及应用

张洋洋，何 丽，刘 琥，吴学雷

（北京航天发射技术研究所，北京，100076）

基于载荷谱的结构疲劳寿命预测技术研究及应用

张洋洋，何 丽，刘 琥，吴学雷

（北京航天发射技术研究所，北京，100076）

机械零件实际受载过程中往往承受复杂的随机载荷，对随机载荷的统计分析是疲劳全寿命设计的重要技术手段。研究了变幅载荷下有限寿命疲劳强度评价和寿命估算方法，结合跑车实测载荷谱，对某特种车辆变速箱输入轴进行了疲劳寿命分析和预测。研究结果表明，这种机械结构的疲劳设计分析方法可为提高地面设备关键零部件的抗疲劳能力研究提供参考。

载荷谱；疲劳；寿命预测；有限元

0 引 言

金属材料在应力或应变的反复作用下所发生的性能退化叫做疲劳破坏[1]。疲劳破坏是工程结构和机械失效的主要原因之一，引起疲劳失效的循环载荷的峰值往往远小于根据静态断裂分析估算出的安全载荷，因此，开展结构疲劳研究有重要意义[2,3]。在汽车工业中，转轴有50%以上是疲劳破坏，而变速器齿轮的疲劳失效高达60%，其他诸如机架、曲轴、齿轮、螺栓和焊接构件等的断裂，疲劳破坏也占很大比例[4]。

近年来，因疲劳产生的结构失效使特种车辆关键部件的安全性和可靠性问题逐渐凸显，但由于分析手段的限制，对该种破坏模式的有效分析和预测工作仍不够系统和完善。由于理论分析难以获得应力集中部位的真实应力，本文在疲劳分析基本原理的基础上对某特种车辆变速箱的传动轴先开展有限元分析，模拟其在最危险工况下的应力分布和载荷历程，再结合具体跑车实测载荷，对其关键部位进行系统的疲劳寿命分析和预测。

1 疲劳寿命预测的有限元方法

传统的结构件疲劳寿命预测方法比较单一，即采用等效载荷方法，通过材料的S-N曲线估算相同载荷下结构的疲劳寿命。此方法方便易行，但对于理论分析难以获得应力集中部位真实应力的问题，该方法并不适用。利用有限元在处理结构静载和动载下响应的巨大优势，本文拟开展基于有限元的结构件疲劳寿命的分析和预测。对理论分析难以获得复杂结构件真实应力的状况，采用基于有限元仿真的疲劳分析方法，获得结构件的实际载荷分布。同时，结合实测的载荷谱，以及材料的S-N曲线，对结构件的关键部位进行系统的疲劳寿命分析和预测，获取结构件的寿命分布云图。该技术路线如图1所示。

图1 有限元法预测结构疲劳寿命技术路线

2 随机载荷及载荷谱统计方法

随机载荷往往是一种不规则的、不能重复的载荷，一般只能使用统计分析方法进行处理。常用的统计分析方法主要有计数法和功率谱法[5]。由于在疲劳强度和可靠性设计中主要关注载荷幅值的变化，因而常用计数法进行分析和处理[1]。雨流计数法是应用较广的计数方法，因为该方法用于累积疲劳寿命估算的结果与试验结果之间有较好的相关性。鉴于雨流法在理论上与疲劳损伤理论密切联系，在应用上具有较高的精确度，并且易于应用计算机进行统计分析，因此国内外对雨流计数法的研究和应用越来越多[6]。在本文的研究中，将采用雨流计数法对实测载荷谱进行统计分析。

雨流计数法与材料的疲劳损伤相结合，是考虑了材料应力-应变行为而提出的一种计数方法。该方法将应力-应变间的非线性关系列入考虑范围，同时计算时考虑了应力统计分析的滞回线和疲劳损伤理论。在雨流计数过程中，应力-时间历程的每一部分都参与计数，且只计数一次[5]。雨流法统计计数原理如图2[5]所示。

由图2b可以看出，2个小循环和1个大循环分别构成2个小的和1个大的滞回线。疲劳损伤由滞回线包围的面积决定，如果认为1个大循环所产生的损伤不受1个小的迟滞回线截断的影响，则可以逐次将构成较小迟滞回线的小循环从整个应变-时间历程中提取出来重新加以组合。这样处理后，图2a的应变-时间历程将简化为图2c的形式，并认为两者对材料引起的疲劳损伤是等效的。图2c中的载荷曲线为规则的交变载荷，可以根据该载荷进行疲劳寿命分析和预测。

图2 雨流计数法原理示意注：图中数字为数据点的标注

3 材料的疲劳特性曲线获取方法

在无材料疲劳寿命曲线的情况下，本研究拟采用FE-SAFE软件中集成的Seeger材料近似算法[7]进行拟合，该估算方法可针对普通碳素钢、低到中合金结构钢、铝以及钛合金等材料进行相对精确的S-N曲线拟合。该拟合方法认为同种类材料的S-N曲线具有相似的疲劳强度系数和疲劳强度指数。例如，对于疲劳特性曲线的Manson-Coffin公式[1]：

式中fσ为疲劳强度系数；b为疲劳强度指数；σΔ为应力范围；fN为疲劳失效寿命。

该方法认为式（1）中的疲劳强度系数和指数对不同种类合金满足表1所示的关系。

为了验证Seeger拟合方法与材料实测S-N曲线的差异，分别选取了FE-SAFE数据库中的AL100-T6铝材和SAE1008铸铁材料[7,8]，并用Seeger方法拟合得到其近似的S-N曲线，如图3所示。

表1 Seeger疲劳特性曲线拟合参数选取方法[7]

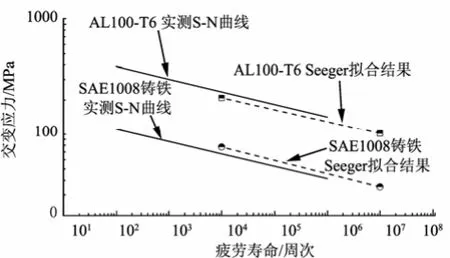
图3 材料实测S-N曲线与Seeger拟合方法对比[7]

由图3可以看出，铝材和铸铁的拟合S-N曲线和实测S-N曲线的差距非常小，而且两者的斜率基本相同。因此经Seeger方法拟合的材料S-N曲线满足计算所需的精度。

4 某特种车辆变速箱输入轴疲劳分析算例

4.1 结构有限元仿真及应力分布

针对某特种车辆底盘变速箱的输入轴开展研究，并以轴肩、环槽等细节为研究对象展开分析。另外，保留了倒角和圆孔等应力集中区域的几何特征。整体采用六面体网格，并采用C3D8R单元类型，以减小计算规模。图4为某特种车辆变速箱输入轴仿真模型及仿真结果。针对轴上的应力集中部位（倒角、圆孔）进行网格细分，保证圆角部位至少有4个网格[9]（见图4a）。为了精确地获取应力集中区域的应力信息，圆角部位采用二次六面体单元C3D20。

有限元模型中边界条件按照输入轴的实际受力情况施加，即在花键处施加1 N·m的单位扭矩，并固定输出端端面的所有自由度。

输入轴结构在1 N·m单位扭矩下的应力云图如图4b所示。由图4b可以看出，该结构在单位扭矩作用下的最大应力约为0.156 4 MPa。

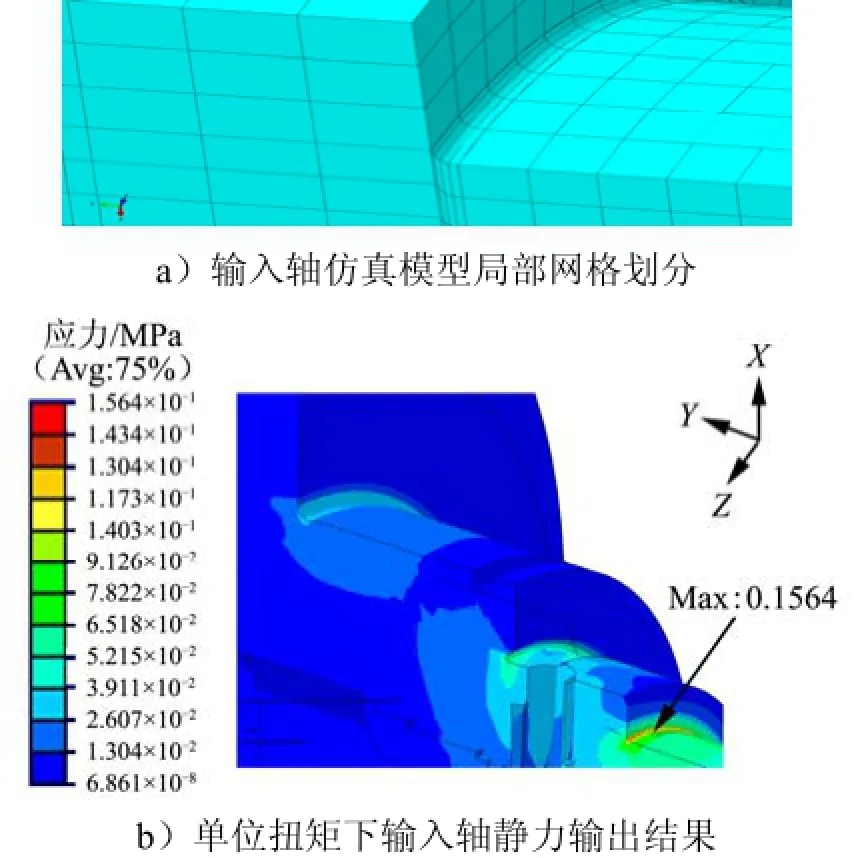
图4 变速箱输入轴仿真模型及仿真结果

4.2 实测跑车扭矩谱及疲劳载荷谱

通过跑车试验得到输入轴的实测转速谱和扭矩谱，采集曲线如图5所示。从图5可以看出，在车辆启动和制动过程中数据波动较大，在正常跑车过程中测试数据相对稳定。因此，为更准确地描述和辨识结构的疲劳特性，需对转速和扭矩测试数据进行截断，并将其截分为启动阶段、运行阶段及制动阶段。

图5 变速箱输入轴实测扭矩谱

采用雨流计数法对实测的随机信号进行统计分析，将其分解为若干条规则的具有恒定均值、幅值、频率的曲线，作为疲劳分析的载荷输入。采用疲劳分析软件FE-SAFE中集成的雨流计数算法开展分析。图6为经雨流计数法处理后的运行阶段交变载荷柱状图。另外，将雨流计数结果转换为FE-SAFE可识别的“.ldf”载荷文件，并导入该软件中作为交变载荷谱。

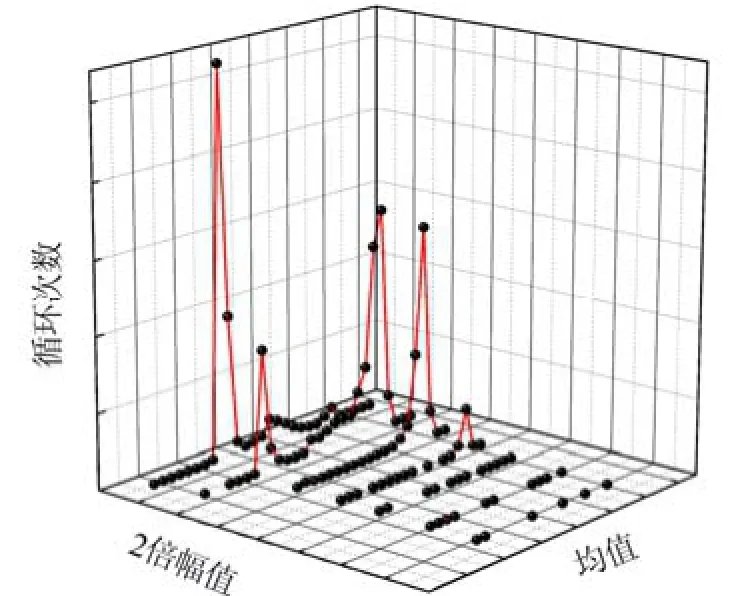
图6 变速箱输入轴在运行阶段交变载荷柱状曲线

4.3 输入轴材料的S-N曲线

使用Seeger方法进行材料性能参数拟合时需要的材料参数包括材料类型、弹性模量及抗拉强度。变速箱轴类零件采用合金材料，材料类型为弹塑性钢材。经Seeger方法拟合得到的材料S-N曲线如图7所示。

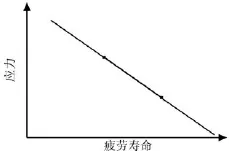
图7 变速箱轴类所用合金材料的拟合S-N曲线

4.4 疲劳分析

材料的疲劳特性曲线是在特定载荷模式下得到的载荷与疲劳寿命的对应关系，在进行结构的疲劳寿命分析与预测时还需要考虑加工精度、理论应力集中、尺寸效应、缺口效应、平均应力等因素的影响。其中理论应力集中、尺寸效应、缺口效应等因素在进行有限元静载分析时已考虑在内，即有限元的静载输出结果已经考虑了局部应力集中效应，因此在疲劳分析软件中仅需对表面加工精度、平均应力的影响进行考虑与设置。FE-SAFE需定义的分析选项如表2所示。

表2 FE-SAFE疲劳分析参数设置

通过FE-SAFE计算输入轴模型的疲劳寿命，并通过Abaqus软件进行后处理分析，轴身疲劳寿命的对数值分布如图8所示。

图8 输入轴局部疲劳寿命云图

由图8可以看出，输入轴的结构安全性能较高，轴身大部分区域的疲劳寿命均达到或超过107次，可认为具有无限寿命。另外，最小疲劳寿命区域出现在圆角根部，为105.59次。由于该结果建立在所有周次的疲劳载荷与图7所示载荷一致的假设基础上，并未考虑花键和齿轮根部的应力集中效应，因此只具有参考价值。后续的研究将针对花键和齿轮等轴上的特征结构开展疲劳寿命分析。

5 疲劳参数灵敏度分析

为了研究不同影响因素对疲劳寿命的影响效应，分别开展输入轴在不同材料性能参数、表面粗糙度及局部结构应力集中系数等条件下相似的疲劳分析，并对比不同测试条件下疲劳寿命的差异，借此提炼设计中应注意的关键影响因素。表3为不同影响因素作用下的最小疲劳寿命对比。

表3 不同影响因素作用下的最小疲劳寿命对比

从表3可以看出，表面粗糙度增大、材料的强度极限降低、结构局部圆角减小（导致应力集中系数增大）等均会造成寿命的降低，且各因素对寿命的影响均为非线性关系。

6 结束语

基于雨流计数法的载荷谱分析方法，对某特种车辆变速箱输入轴的疲劳寿命进行分析和预测，利用该疲劳分析技术，探讨了材料性能、表面粗糙度以及局部应力集中效应对结构疲劳寿命的影响效应。该研究提供了一种机械结构的疲劳设计分析方法。该方法可识别影响结构疲劳寿命的关键设计要素，并建立系统的程序块，提高产品疲劳寿命的快速分析和预测能力。未来可能建立整车全方位的疲劳寿命分布图，从而为特种车辆关键零部件的抗疲劳设计研究提供参考。

[1] Suresh S. 材料的疲劳: 第二版[M]. 王中光等, 译. 北京: 国防工业出版社, 1999.

[2] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2004.

[3] 吴胜君, 徐有良. 轻型汽车变速箱第一轴的疲劳分析[J]. 机械设计与制造, 2008(5): 111-112 .

[4] 朱元佳. 汽车变速箱在线快速故障诊断技术研究[D]. 上海: 同济大学, 2007.

[5] 周家泽, 管昌生. 机械零件随机疲劳载荷的统计分析方法[J]. 襄樊职业技术学院学报, 2003,2(4): 4-7.

[6] 郭小鹏, 沙云东, 柏树生, 等. 基于雨流计数法和功率谱密度法的随机声疲劳应用研究[J]. 航空发动机, 2010(5): 26-31.

[7] Safe Technology Limited. Fatigue Theory Reference Manual[R]. 2001.

[8] 成大先. 机械设计手册: 单行本[M]. 北京: 化学工业出版社, 2004.

Application and Study on Load-spectrum-based Fatigue Life Prediction Technique

Zhang Yang-yang, He Li, Liu Hu, Wu Xue-lei
(Beijing Institute of Space Launch Technology, Beijing, 100076)

The statistical analysis of the load spectrum for engineering component is the basis for design and fatigue life prediction, and also a key foundation for whole-life fatigue design. However, fatigue loads always randomly vary with time, which make the determination of random fatigue load very complicated. This article discusses the fatigue life prediction method for varying load conditions. In association with the tested load spectrum, fatigue analysis has been conducted on a input shaft of a gear box. The method proposed by this article is an effective way for fatigue analysis and design, and can be used as useful guidance in improving the anti-fatigue ability for the key components of land-based equipments.

Load spectrum; Fatigue; Life prediction; Finite element method

V553.1+9

A

1004-7182(2016)04-0078-05

10.7654/j.issn.1004-7182.20160420

2015-09-30；

2016-07-08

张洋洋（1988-），男，工程师，主要从事结构刚强度分析、疲劳及断裂失效研究