勾股与中考

□田全静



勾股与中考

□田全静

考点1：直角三角形的判定

例1（呼和浩特）如图1，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（）.

图1

A. CD、EF、GH

B. AB、EF、GH

C. AB、CD、GH

D. AB、CD、EF

分析：此题先根据网格图计算出AB2、DC2、EF2、GH2，再看哪两条的平方和等于第三条的平方，就可以判断出哪三条线段能构成一个直角三角形的三边.

解：在Rt△ABE中，

BE＝2，AE＝2，

根据勾股定理得AB2＝AE2＋BE2＝22＋22＝8.

同理可得EF2＝12＋22＝5，

CD2＝22＋42＝20，

GH2＝32＋22＝13.

而AB2＋EF2＝GH2，故选B.

考点2：勾股定理的证明

例2（温州）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感.他惊喜地发现：当两个全等的直角三角形如图2或图3摆放时，都可以用“面积法”来证明.下面是小聪利用图2证明勾股定理的过程：将两个全等的直角三角形按图2所示摆放，其中∠DAB＝90°，求证：a2＋b2＝c2.

图2

图3

证明：连结DB，过点D作△DCB 的BC边上的高DF，则DF＝EC＝b-a，

∴a2＋b2＝c2.

请参照上述证法，利用图3完成下面的证明：

将两个全等的直角三角形按图3所示摆放，其中∠DAB＝90°.

求证：a2＋b2＝c2.

证明：连结________

∵SACBED＝________

又∵SACBED＝________

∴________，

∴a2＋b2＝c2.

解答与前面类似，略.

考点3：勾股定理的应用

例3（达州）如图4，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点G、F分别在AB、BC上（含端点），且AB＝6，BC＝10. 设AE＝x，则x的取值范围是______.

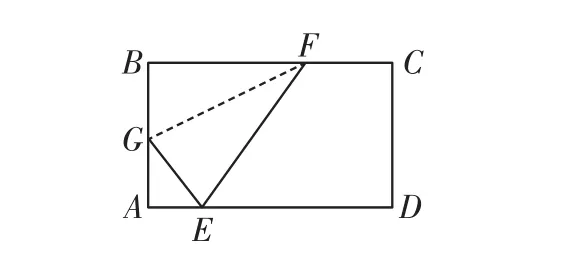
图4

解析：①如图5，当G与A重合时，x取得最大值，AE＝AB＝6，则x≤6.

②如图6，当F与C重合时，x取得最小值，EF＝BC＝10，

AE＝10-8＝2，则x≥2.

因此2≤x≤6.

图5

图6

例4（温州）我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图7）.图8由弦图变化得到，它是由八个全等的直角三角形拼接而成.记图8中正方形ABCD、正方形EFGH，正方形MNKT的面积分别为S1、S2、S3，若S1＋S2＋S3＝10，则S2的值是______.

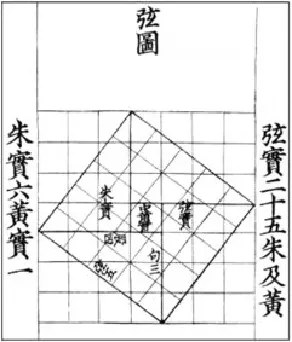
图7

图8

解析：由题意可设：CG＝NF＝b，CF＝DG＝KF＝a，GF＝c，

则S1＝（a＋b）2，S2＝c2，S3＝（ab）2，又S1＋S2＋S3＝10，

∴（a＋b）2＋c2＋（a-b）2＝10，

∴2a2＋2b2＋c2＝10.

根据勾股定理有a2＋b2＝c2，

∴S2的值是