基于区间直觉梯形模糊数的多属性群决策方法

邹　斌

(安徽广播电视大学　公共基础部，合肥　230022)



基于区间直觉梯形模糊数的多属性群决策方法

邹斌

(安徽广播电视大学公共基础部，合肥230022)

摘要：针对专家和属性权重完全未知的区间直觉梯形模糊数的多属性群决策问题，根据定义的区间直觉梯形模糊数的交叉熵求解专家权重，结合灰色关联分析法定义了综合关联系数和综合关联度，依据所有决策方案的综合关联度最大化的思想构建模型得到属性权重公式，并给出基于IITFN-WAA算子的群决策步骤，最后通过实例分析验证决策方法的合理性。

关键词：区间直觉梯形模糊数；交叉熵；多属性群决策；综合关联度

0引言

目前，灰色关联理论应用于多属性决策方面的研究已取得较大进展，文献[1]提出了灰色关联的概念以及灰色关联度的计算公式，为灰色关联思想奠定了理论基础。文献[2]基于矩阵型灰色聚类分析，解决了一种面向对象多属性差异问题，根据属性间的差异进行类别组合，从而获得多元、客观的聚类结果，使对象的分类更贴近实际。文献[3]依据指标白化权函数值离差最大化的思想，构建灰色聚类模型来确定属性权重并给出最优方案的确定方法。

文献[4-5]将直觉模糊隶属度拓展到区间上，建立数学模型对区间数灰色模糊进行综合评判，使决策结果更加直观可信。但基于灰色思想的区间直觉模糊数决策问题的应用相对较少，文献[6]通过定义区间直觉模糊数的距离公式和灰关联系数，对权重信息部分未知的属性权重进行求解，来确定方案的优势度。文献[7]利用区间直觉模糊数的运算法则和性质得到各时间段的正负理想解，并根据与正负理想方案的灰色关联度差异最小化建立优化模型，从而对方案进行评价。

而利用灰色关联思想来解决区间直觉梯形模糊数的决策问题还处于初级阶段。因为区间直觉梯形模糊数综合考虑了属性的各种情况，能更好的体现出决策信息的不确定性和模糊性，可以更为真实地体现决策者的本意。因此，针对区间直觉梯形模糊数环境下的多属性决策问题的研究具有更宽广的前景及现实意义。

1预备知识

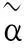
非隶属度为

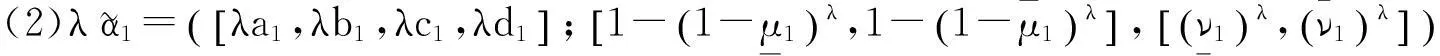
(1)

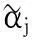
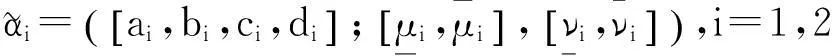
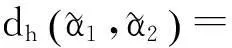
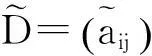
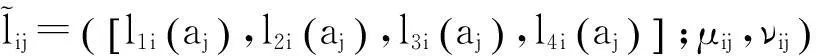
(2)

(3)

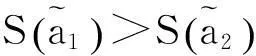
2问题描述

下面针对专家和属性权重均未知且属性值以区间直觉梯形模糊环境下的多属性决策问题，采用灰色关联分析方法，具体决策方法如下：

首先，根据文献[11],对模糊矩阵进行规范化。

其次，考虑到在同一属性下可以用某专家与所有专家的差异度来确定专家权重。在实际问题中，在同一属性下，某专家所给出的方案属性的区间直觉模糊信息与其他专家的差异越大，说明该专家越偏离群体决策者，则该专家的权重就越小。因此，本文采用交叉熵来确定某专家与其他专家的区别程度，从而确定专家权重。

根据文献[12]，将交叉熵推广到区间直觉梯形模糊数，即有下面定义。

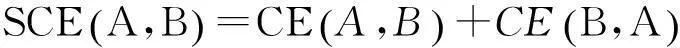
2.1专家权重求解步骤

(2)求得专家dk与群体决策者在方案ai下的交叉熵:

(3)求得专家dk与群体决策者在所有方案下的交叉熵:

(4)

(4)计算专家权重:

(5)

2.2属性权重确定

首先，根据公式(1)得到每位专家集成后的区间直觉梯形模糊决策矩阵。

然后，基于灰色关联分析，方案xi在属性aj下的正相关系数为:

(6)

方案xi在属性aj下的负相关系数为

(7)

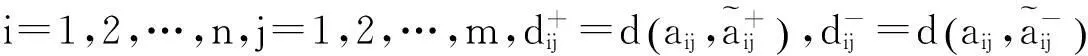
方案xi在所有属性下的综合关联度为:

(8)

对于每个方案xi来说，其综合关联度ri总是越大越好，越大离正理想解距离越近，离负理想解越远。基于此思想建立如下规划模型:

构造Lagrange函数解此最优化模型:

求偏导，并令

计算出最优解：

(9)

2.3决策方法

综上所述，基于区间直觉梯形模糊信息环境下的专家和属性权重均未知的多属性群决策问题的步骤如下，

Step 1：对原始模糊决策矩阵进行规范化；

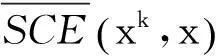
Step 3：由(5)确定专家权重λk，k=1,2,…,t。；

Step 6：由(8)求得各方案的综合关联度ri，并根据ri的大小对决策方案xi择优。

3实例分析

表1　专家1的规范化决策矩阵

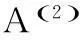
表2　专家2的规范化决策矩阵

表3　专家3的规范化决策矩阵

则专家d1与专家d2在方案a1下的交叉熵为：

根据(4)得专家d1与群体决策者在所有方案下的交叉熵

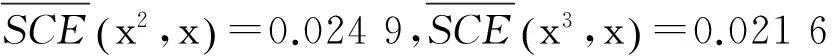
由(5)确定专家权重:

根据(6)和(7)得到综合关联系数矩阵:

ω2=0.268 4，ω3=0.263 0，ω4=0.203 0

由(8)得到每个方案的综合关联度:

r1=0.822 6，r2=0.950 4，r1=0.989 4

对各综合关联度进行排序，则有

x3≻x2≻x1

即x3为最佳方案。

4结语

本章针对专家和属性权重均未知的区间直觉梯形模糊数的多属性群决策问题，定义了区间直觉梯形模糊数的交叉熵来确定专家权重，并依据正、负关联系数给出了综合关联系数和综合关联度的定义，利用所有决策方案的综合关联度最大化建立优化模型来求解属性权重公式，而后根据综合关联度的大小进行择优，并将其应用于多属性决策中，最后通过实例验证决策方法的合理性。

参考文献：

[1]刘思峰，郭天榜，党耀国.灰色系统理论与应用[M].北京:科学出版社， 1999:30.

[2]刘红旗，方志耕，李维东，等.面向对象多属性差异的矩阵型灰色聚类方法及其应用[J].控制与决策， 2015， 30(2): 366-370.

[3]董一哲， 党耀国. 基于离差最大化的灰色聚类方法[J]. 系统工程理论与实践， 2009 (9):141-146.

[4]卜广志，张宇文.基于三参数区间数的灰色模糊综合评判[J].系统工程与电子技术，2001，23 (9):43-46.

[5]朱绍强，孟科，张恒喜.区间数灰色模糊综合评判及儿应用[J].电光与控制，2006，13(3):36-38.

[6]曹薇，牛冲槐，樊燕萍.基于区间直觉梯形模糊数MADM问题的GRA 法[J]. 太原理工大学学报， 2013 (2): 246-250.

[7]刘勇，刘思峰，赵焕焕，等.基于区间直觉模糊的动态多属性灰色关联决策方法[J]. 控制与决策， 2013， 28(9): 1303-1308.

[8]王坚强.模糊多准则决策方法研究综述[J].控制与决策, 2008, 23(6):601-607.

[9]万树平.基于区间直觉梯形模糊数的多属性决策方法[J]. 控制与决策， 2011，26(6):857-860.

[10] 万树平.基于分式规划的区间梯形直觉模糊数多属性决策方法[J].控制与决策，2012，27(3):455-458.

[11] 付亚男,毛军军, 徐丹青. 基于交叉熵的 ITFN 的多属性决策方法[J]. 计算机工程与应用, 2014, 50(20): 218-222.

[12] Ye J. Fuzzy Cross Entropy of Interval-valued Intuitionistic Fuzzy Sets and its Optimal Decision-making Method Based on the Weights of Alternatives[J]. Expert Systems with Applications， 2011， 38(5): 6179-6183.

[责任编辑：张永军]

Multiple Attribute Group Decision Making Method Based on Interval-valued Intuitionistic Trapezoidal Fuzzy Numbers

ZOU Bin

(Department of Basic Courses, Anhui Radio and TV University，Hefei 230022,China)

Abstract:focus on the multi-attribute group decision making problem, in which the attribute values are interval-valued intuitionistic trapezoidal fuzzy number and the expert and attribute weights are complete unknown, according to the definition of cross entropy to solve the expert weights, defining comprehensive correlation coefficient and the degree of comprehensive correlation make use of grey correlation, constructing the model on basis of the maximizing the degree of comprehensive correlation, giving the corresponding group decision method of IITFN-WAA operator. Finally, the expediency of the decision making methods are verified by practical example.

Key words:interval-valued intuitionistic trapezoidal fuzzy numbers;cross entropy;multiple attribute group decision making;comprehensive correlation

中图分类号：O159

文献标识码：A

文章编号：1673-162X(2016)01-0013-07

作者简介：邹斌(1981—)，男，安徽六安人，安徽广播电视大学公共基础部讲师，硕士。

项目基金：2016年高校优秀青年人才支持计划重点项目(gxyqZD2016453)、安徽广播电视大学青年基金项目(qn15-20)资助。

收稿日期：2015-10-15修回日期：2015-12-28