Infrared Small-target Detection Using The Maximum of Second-order Directional Derivative

ZHAO Ai-gang, WANG Hong-li, YANG Xiao-gang, LU Jing-hui, JIANG Wei, QI Nai-xin

(1. Department of Control and Engineering, Rocket Force Engineering University, Xi’an 710025, China;2. School of Sergeancy, Rocket Force Engineering University, Qingzhou 262500, China)*Corresponding Author, E-mail: wanghongli_1965@163.com



Infrared Small-target Detection Using The Maximum of Second-order Directional Derivative

ZHAO Ai-gang1,2, WANG Hong-li1*, YANG Xiao-gang1, LU Jing-hui1, JIANG Wei1, QI Nai-xin1

(1.DepartmentofControlandEngineering,RocketForceEngineeringUniversity,Xi’an710025,China;2.SchoolofSergeancy,RocketForceEngineeringUniversity,Qingzhou262500,China)*CorrespondingAuthor,E-mail:wanghongli_1965@163.com

In order to improve the detection rate of infrared small-target in complex environment, a infrared small-target detection algorithm based on the maximum of second-order directional derivative was proposed. Firstly, the properties of second-order directional derivative were analyzed, meanwhile, the flat component and edge of background were removed by threshold and flip operations of the maximum. Then, the background was predicted based on facet model and further enhanced the small-target by prediction error as weight. The above two steps can be achieved by four convolutions and the detection speed was accelerated. At last, the local contrast of candidate small-targets was calculated to reduce the false alarm rate. The experimental results show that the average signal to clutter ratio gain is 78.413 0 and the average background suppression factor is 35.079 6 in 6 kinds of complex background. The proposed detection algorithm has stronger robustness and higher detection rate.

computer vision; facet model; directional derivative maximum (DDMax); infrared small-target

1 Introduction

Infrared small-target detection is a key technique in large amounts of practical projects such as infrared warning and defense alertness, in which not only accuracy is needed but also speed is required. Owing to atmospheric transmitting and scatter phenomenon, the small-target is usually weak compared with heavy background clutters. According to SPIE (Society of Photo-optical Instrumentation Engineers), the area of small-target is less than 80 pixels in 256×256 image. Obviously, small-target generally occupies only a few pixels[1]in infrared image and has no obvious structure or texture, so the infrared small-target detection is still a challenging issue.

In recent years, numerous infrared small-target detection algorithms have been proposed for different application environment,e.g., cloud-clutter background, sea-wave background and so on, but many of them can’t detect small-target in backgrounds of other type effectively. In a general way, the feature of small-target that many methods based on can be broadly divided into three categories: unsmoothing,i.e. discontinuousness in the region of transition, isotropic gradient and contrast difference of small-target and background. However, the first feature is usually exploited by sparse representation for small-target[2], low-rank character of background[3]and high-pass filter[4],etc., and these methods can get good detection performance in slow-change backgrounds, but their application may be restricted by sharp edge and requirement of high-speed detection. Based on isotropic gradient, Qietal.[4]introduced the second-order directional derivative (SODD) including four directions to distinguish small-target and background; Luetal.[5]designed medial filter using eight directional gradients to highlight isotropic gradient of small-target. The two methods all used facet model to measure directional gradient, but the selection of direction lacks convinced theory. Lately, human visual saliency (HVS) is introduced to infrared small-target detection and acquired many positive achievement[6]. In a sense, HVS is based on contrast difference between salient region,i.e. small-target and background, and if only HVS is used in detection method, it may be affected by the background clutter with similar structure.

Different from traditional infrared small-target detection methods, in this letter, a robust infrared small-target detection algorithm combining three main features[7]of small-target is proposed to seek a better performance in detection rate, false alarm rate, and detection speed simultaneously. It consists of three stages which represent three features,i.e. isotropic gradient, unsmoothing and contrast difference. Isotropic gradient is charactered as maximum of second-order directional derivative derived from the facet model and the unsmoothing is described as predicted error of background. The benefit of aforementioned two features is anti-noise and resistant to background clutter which usually has local orientation. Thus, it can improve robustness and detection ratio of the proposed detection algorithm named robust directional derivative maximum-based (RDDMax) algorithm. Moreover, computational detail of the first two stages mainly contains four convolution operations and firmly believed that it can effectively accelerate detection speed. At last, we introduced minimum local contrast measure (MinLCM) over a few pixels to further reduce false alarm.

2 Design of DDMax Filter

Inspired by the fact that background is continuous and small-target is relatively isolated, we find that the character of different directional derivative can distinguish the small-target and background, but we don’t know which local direction has the best potentiality for detection small-target in advance. In order to solve this problem, DDMax filter is proposed owing to the responses for ramps, stripes and uplifts in infrared images. It can transform background clutter and small-target into almost flat texture and Gaussian-like spots, respectively. For explaining this phenomenon, a compared procedure of processing image using fixed directional derivative filter and the DDMax filter is displayed in Fig.1. The original image (see Fig.1(a) and Fig.1(b)) contains three structures,i.e. ramp, strip and uplift representing slow-change clutter, fast-change clutter and small-target, respectively. Fig.1(c) and Fig.1(d) are horizontal and vertical second-order directional derivative maps of Fig.1(a). From the appearance of orthogonal second-order directional derivative, we can see that the strip is completely different, but the ramp and the small-target are almost the same in two orthogonal directions. Obviously, only these cues are not enough to distinguish small-targets and background clutters. Furthermore, the minimum and maximum maps of second-order derivative in every direction are expressed in Fig.1(e) and Fig.1(g), respectively. Corresponding amended maps are showed in Fig.1(f) and Fig.1(h), in which three components have different responses: the ramp is almost smoothed under two situations; the strip is obviously sharpened in Fig.1(f) and disappeared in Fig.1(h);as for the uplift, observation from the several maps (see Fig.1(c)-Fig.1(h)) shows that the shape of small-target keeps similar especially below the reference plane. Considering the fact that strip and ramp can be filtered away in the amended map of directional derivative maximum, we designed DDMax filter to highlight the isotropic gradient of small-target which is described below in details.

Fig.1 Results of processing image using different directional derivative. (a) Original image. (b) 3D mesh of (a). (c) Horizonal. (d) Vertical. (e) Minimum. (f) Amender of (e). (g) Maximum. (h) Amender of (g).

With the advantage of smoothing and anti-noise, facet model is widely used in detection of gradient edge, super-resolution reconstruction and noise removal,etc., so we also use the facet model to design the DDMax filter. First, we sketch the theory of facet model and derive expression of second-order directional derivative from it. Then, directional derivative maximum can be acquired through maximization of aforementioned expression and has a simple form reduced from four quadrants in image coordinate.

The facet model is actually a bivariate cubic function in which row and column are independent variables and gray-level intensity is dependent variable, that is to say, given a patch of image, building a fitting function with optimized coefficients makes fitting error minimum. For details, defineR={-2,-1,0,1,2},C={-2,-1,0,1,2}, and the 5×5 window for a pixel can be denoted byR×C, in which the center pixel is at (0,0). Then, in a fixed neighborhood window, the gray-level intensity of pixels inR×Cis calculated as follows:

wherePi(r,c)={1,r,c,r2-2,rc,c2-2,r3-(17/5)r,(r2-2)c,r(c2-2),c3-(17/5)c},(r,c)∈R×Cis the set of discrete orthogonal polynomials andKiis the corresponding coefficient. Here, we only use the character of the center pixel and then let the facet model scan the whole image. Given (1), the second-order partial derivatives are evaluated along the row and column at the center pixel (0,0) inR×Cas follows:

(2)

The second-order directional derivative of center pixel along vectorlrepresenting a ray is described as follows:

2K4cos2α+2K5cosαcosβ+2K6cos2β,

(3)

whereαis the angle between the rayland they-axis (row of image) andβis the angle between the rayland thex-axis (column of image). In Fig.2, we divided the image plane into four quadrants and the angle of the raylwas marked.

Based on aforementioned analysis, the maximum of expression (3) is our demanded result and the mathematical language is described as follows:

Fig.2 Sketch of angles (α, β) in image coordinate

(4)

whereGMaxis the maximum of expression (3), angleαandβhave special fixed relationship expressed as below:

(5)

Expression(5)includesallpossiblesituations,andweonlyprovideexplicitcalculationprocessforEq.(4)inquadrantone.Theremainingthreesituationshavesimilarreductionandfinalresultsaregivenlatter.Inquadrantone,cosβ=cos(π/2-α)=sinαis substituted in Eq.(4), and we can get the following form:

(6)

Inordertoseekthemaximum,calculatingthederivativeofGMaxwith respect toα, the maximum condition onαfor Eq.(6) can be obtained as follows:

-2(K4-K6)sin2α+2K5cos2α=0.

(7)

Basedontherelationship:sin22α=1-cos22α,Eq.(7) can be transformed to the following form:

(8)

And then, let Eq.(8) get into Eq.(6) in which sin2α≥0, so Eq.(6) can be turned into the following form:

(9)

In addition to quadrant one, other three quadrants have the similarly results, and finally total results can be expressed as follows:

(10)

In order to get the maximum of four quadrants, make sure the second term of above expression is positive, and then Eq.(10) is transformed to the following form:

(11)

Obviously, Eq.(11) has three relatively separate terms and can be denoted as follows:

(12)

whereK4-6=K4-K6andK4+6=K4+K6. Note that the coefficientKi(i=4,5,6) is related to different pixels (x,y) in the whole image rather than fixed small facet. Similarly,GMaxis also corresponding with every pixel in image and Eq.(12) is turned into the following form:

(13)

Afterwards,wedenotedthecoefficientKi(i=4,5,6) asKi(x,y)(i=4,5,6) to avoid confusion. According to least squares surface fitting and orthogonal property of polynomials, the coefficient can be calculated in the following form:

(14)

whereI(x,y) is the gray-level intensity of the pixel (x,y) in the image. Based on the convolution form of Eq.(14),Ki(x,y) can be computed efficiently with the following convolution kernel:

(15)

And then, Eq.(13) can be obtained by simple arithmetic operation and three convolutions with corresponding convolution kernels described as follows:

(16)

At last, Eq.(13) can be finished by three convolutions and the result is similar to Fig.1(g). However, note that the center of small-target in DDMax map (see Fig.1(g)) obtained by Eq.(13) is less than zero, whereas the neighborhood values are larger than zero. In order to highlight the small-target and depress background clutters, DDMax filter operation needs to amend the DDMax map by subsequent steps:(1) Calculate mean of pixels in DDMax map that gray-level intensity is less than zero and use five times of mean as threshold; (2) In the DDMax map, set pixels that gray-level intensity is larger than designed threshold to be zero; (3) Inverse the whole DDMax map up and down;(4) Normalize the values to a fixed rang [0,1]. After modification, the small-target is above the base plane and other components of background are disappeared.

3 RDDMax for Infrared Small-target Detection

When small-target appears in background, it may bring about unsmoothing owing to different infrared character. However, the facet model can capture this phenomenon using large predicted error, when the center pixel is approximated by the pixels in its neighborhood. Given Eq.(1), the center pixel can be expressed by facet model and the approximation of every pixel in image has the following form:

(17)

EP(x,y)=I(x,y)-K1(x,y)+2×

K4(x,y)+2×K6(x,y),

(18)

inwhichK1(x,y),K4(x,y), andK6(x,y) can be obtained by Eq.(14). while theI(x,y) can be written in the same form with convolution kernel expressed as follows:

(19)

Consequently, Eq.(18) can be achieved by once convolution with a combined convolution kernel:

WE=W-W1+2×W4+2×W6=

(20)

Andthen,wefindthatthepredictederrorofbrightblobsislargerthanzero,whiletheoneofdimblobsislessthanzero.Forthisreason,weonlypreservethevaluesthatarelargerthanzeroandremoveothers.SothemodifiedversionofEq.(18)isexpressedasfollows:

(21)

Inordertogiveconsiderationtoisotropicgradientandunsmoothingsimultaneously,EPM(x,y) is required to be normalized in a fixed range [0,1] before combination operation described as follows:

(22)

After the aforementioned step, there still may be some false small-targets, soGE(x,y) map needs further processi.e. minimum local contrast measure to locate the true small-target. Analysis about MinLCM is shown in Fig.3.

Over a fixed pixel (x,y) that is defined as center point, construct an 3×3 image patch which is surrounded by eight neighborhoods with the same size and define local contrast measure as follows:

Fig.3 Sketch of local contrast measure

(23)

where Max[Ip(x,y)] and Mean[In(x,y)] are maximum and mean operations respectively, andIP(x,y) is center patch, whileIn(x,y) is neighborhood patch shown in Fig.3. The minimum of eight LCMs over background no matter clutter or edge region is usually small. However, whenIP(x,y) is located in the small-target region, everyCn(x,y) must be large and the smallest one is still larger than other locations. So the MinLCM can distinguish small-target and background, and then Eq.(22) can be modified by the following form:

(24)

whereIGEP(x,y) has the same size withIP(x,y) and only scans theGE(x,y) map without any neighborhood. Although Min[Cn(x,y)] has large computation complexity, the amount of pixels that needs this operation is very small,i.e. about 0.2%. It is indisputable that this process can further inhibit the background clutters and amplify the isotropic small-target.

RDDMax method combines three features together to detect infrared small-target target using efficient convolution. Specially, Fig.4 shows a flow diagram of acquiring the small target saliency map by RDDMax method. First, the original infrared image is filtered by DDMax filter containing three parallel convolutions and amending process; Second, predicted error map is finished by one convolution and is fused with the DDMax map; Finally, the combined map needs further process with MinLCM for a few false targets.

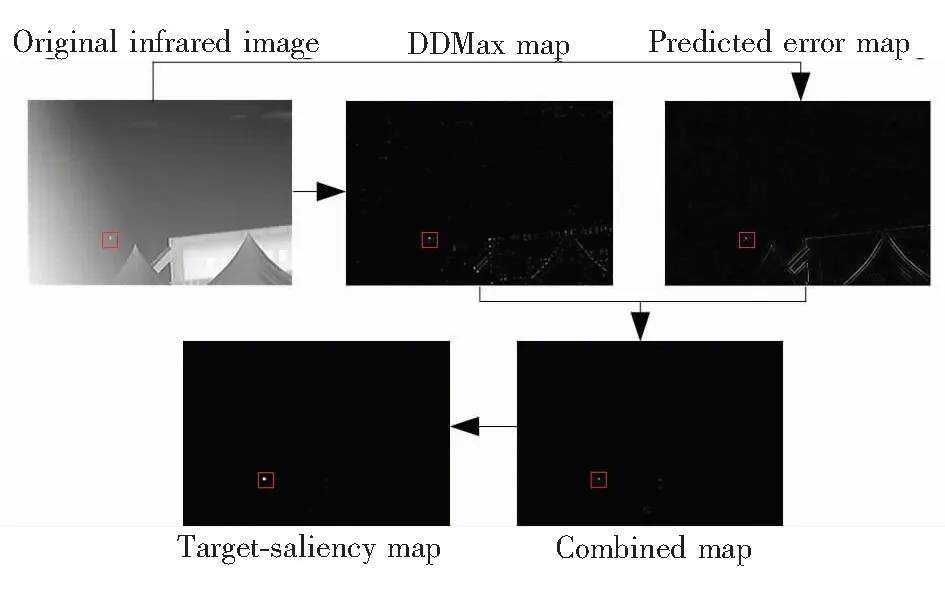
Fig.4 Flow diagram of RDDMax detection algorithm

Detailed steps of RDDMax algorithm for infrared small-target detection are described as follows:

Step 1 Do convolutions between three reduced kernels expressed in Eq.(16) and original infrared image to compute three independent components of Eq.(13) for each pixel.

Step 2 In order to acquire DDMax map, Calculate Eq.(13) and amend the result using guidance described in final part of section Ⅱ(A).

Step 3 Compute predicted error map based on facet model using one convolution and preserve values that are larger than zero, finally, normalize values to a fixed range [0,1].

Step 4 Combine DDMax map and predicted error map by the means of Eq.(22) to fuse the isotropic gradient and unsmoothing.

Step 5 Calculate MinLCM for a few pixels in raw infrared image and multiply the combined map to form the target-saliency map.

Step 6 Choose the segmentation threshold which is twice of the mean (an empirical value from experiments) to extract small-targets from the target-saliency map.

4 Experiments

In order to validate the performance and robustness of the RDDMax algorithm for infrared small-target detection, experiments on six infrared images of different typical backgrounds have been done by VS2012+Opencv software on a PC with 4 GB memory and 3.3 GHz Intel i3 dual processor. In addition, the collecting image device is a cooled HgCdTe IR detector with resolution of 320×240. Part images are obtained from China international general aviation convention in 2015 which include tree-wire (see Fig.5(a)), sky-building (see Fig.4 and Fig.5(b)), heavy cloud (see Fig.5(c)), and other infrared images come from the internet that contain sea-wave (see Fig.5(d)) and tree-fork (see Fig.5(e)). All the small-targets are all less than 9×9 which is corresponding to the definition by the Society of Photo-Optical Instrumentation Engineers (SPIE).

4.1 Results Using the Proposed Algorithm

Raw infrared images are processed by steps described in section Ⅲ to acquire the target saliency maps(see the last column of Fig.5), in which most background clutters no matter how complex are suppressed and small-targets are all highlighted in the images. For different background clutters, the response of DDMax or predicted error is diversified, even existing terrible situations, for example, predicted error map of Fig.5(e) is negative for detection owing to a large amount of noises, and DDMax map of Fig.5(c) has a lot of disordered points in the region of clutters. However, the final target saliency map is easy to extract small-target, because the DDMax map and predicted error map are complementary in most cases and together highlight the small-targets(see Fig.5(e)). Specially, although in Fig.5(b) the small-target is submerged in the heavy cloud, and the DDMax map as well as predicted error map is affected by the clutters of light and shadow, the response of small-target is larger than background clutters and the MinLCM can help to detect the small-target accurately.

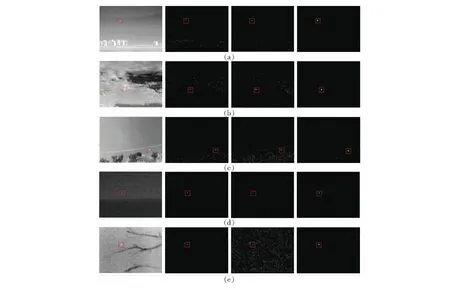
Fig.5 Detection process of RDDMax algorithm for five images, in which from left to right there sequentially are raw infrared images, DDMax map, predicted error map and target saliency map.

4.2 Comparison with Other Detection Algorithms

In order to have a fair comparison, target saliency map of each method without threshold operation takes part in evaluation, and the five compared algorithms are programed on the same software platform, including morphological detection (Tophat) method[8], facet-based (Facet) method[9], least squares support vector machine-based (LSSVM) method[10], seconder order directional derivative filter-based (SODD) method[4], minimum local contrast measure-based (MinLCM) method[11]. Firstly, we draw receiver operation characteristic (ROC) curve for each method to provide a directly visual comparison of detection performance. In general, the ROC curve reflects the varying relationship of detection probabilityPdand false alarm ratePf. Meanwhile, they are defined as follows:

(25)

Fig.6 Comparison of ROC curves with six methods for each test image

In Fig. 6, the results show that RDDMax method has better performance than other five methods, which indicate that the false alarm rate of the proposed method is usually lower under the same detection probability. That is to say, RDDMax method is more accurate and consistent than other methods for detection infrared small-target. Note that the SODD method can also get good ROC curves for some images (see Fig.6(d) and Fig.6 (f)). However, this method is not stable and has high false alarm rate owing to the fixed directional derivative. For other method, detection probability and false alarm rate are all in the dominant position obviously. In a word, the RDDMax method really shows its good performance and robustness for small-target detection under different complex backgrounds.

Furthermore, Tab.1 shows three common evaluation indicator including detection time, signal clutter rate gain (SCR Gain) and background suppression factor (BSF) defined as follows:

(26)

whereSrepresents amplitude difference of signal and clutter, andCis the standard deviation of background clutter. Meanwhile, the subscriptsinandoutexpress the state before and after detection. SCR Gain describes the degree of detection difficulty and BSF measures the suppression ability of detection algorithm. The numerical value is larger, the performance is better. From Tab.1, we can see that RDDMax method has good performance in SCR Gain and BSF. Although the value is not always the highest, the value is higher than other four methods and the mean of six images with difference background is the highest. The reason for a little lower SCR Gain and BSF of Fig.5(a) is that the bright buildings have similar Gaussian-like shape to small-target and can deceive the RDDMax method in some degree. For detection time, the proposed method is the second fastest and can achieve the requirement of real-time treatment.

Tab.1 Evaluation indicators of six detection methods

5 Conclusion

In this article, we have proposed an RDDMax method for infrared small-target detection mainly inspired by isotropic gradient for small-target. Meanwhile, unsmoothing and local contrast measurement are considered to enhance the small-target in the proposed method. In order to evaluate the comprehensive performance and robustness of RDDMax method, real infrared images with different complex backgrounds and five other methods are used in the experiments. Average signal to clutter ratio gain is 78.413 0 and the average background suppression factor is 35.079 6.The evaluation indicators show that the designed method has better performance and robustness than the state-of-the-art methods.

[1] ZHANG F, LI C F, SHI L N. Detecting and tracking dim moving point target in IR image sequence [J].InfraredPhys.Technol., 2005, 46(4):323-328.

[2] GAO C Q, ZHANG T Q, LI Q. Small infrared target detection using sparse ring representation [J].IEEEAerosp.Electron.Syst.Mag., 2012, 27(3):21-30.

[3] WANG C Y, QIN S Y. Adaptive detection method of infrared small target based on target-background separationviarobust principal component analysis [J].InfraredPhys.Technol., 2015, 69:123-135.

[4] QI S X, MA J, TAO C,etal.. A robust directional saliency-based method for infrared small-target detection under various complex backgrounds [J].IEEEGeosci.RemoteSens.Lett., 2013, 10(3):495-499.

[5] 卢瑞涛，黄新生，徐婉莹. 基于Contourlet变换和Facet模型的红外小目标检测方法 [J]. 红外与激光工程， 2013, 42(8):2281-2287. LU R T, HUANG X S, XU W Y. Method of infrared small target detection based on contourlet transform and facet model [J].InfraredLaserEng., 2013, 42(8):2281-2287. (in Chinese)

[6] CHEN C L P, LI H, WEI Y T,etal.. A local contrast method for small infrared target detection [J].IEEETrans.Geosci.RemoteSens., 2014, 52(1):574-581.

[7] WANG X, LV G F, XU L Z. Infrared dim target detection based on visual attention [J].InfraredPhys.Technol., 2012, 55(6):513-521.

[8] BAI X Z, ZHOU F G. Analysis of new top-hat transformation and the application for infrared dim small target detection [J].PatternRecognit., 2010, 43(6):2145-2156.

[9] WANG G D, CHEN C Y, SHEN X B. Facet-based infrared small target detection method [J].Electron.Lett., 2005, 41(22):1244-1246.

[10] WANG P, TIAN J W, GAO C Q. Infrared small target detection using directional highpass filters based on LS-SVM [J].Electron.Lett., 2009, 45(3):156-158.

[11] HAN J H, MA Y, ZHOU B,etal.. A robust infrared small target detection algorithm based on human visual system [J].IEEEGeosci.RemoteSens.Lett., 2014, 11(12):2168-2172.

赵爱罡(1986-)，男，河北衡水人，博士研究生，2012年于燕山大学获得硕士学位，主要从事红外精确制导、目标识别、机器视觉等方面的研究。

E-mail： zhaoaigang1986120@163.com

王宏力(1965-)，男，陕西凤翔人，教授，博士生导师，1999年于火箭军工程大学获得博士学位，主要从事导航制导与控制、复合制导、天文/惯性导航等方面的研究。

Email： wanghongli_1965@163.com

利用二阶方向导数极大值检测红外小目标

赵爱罡1,2， 王宏力1*， 杨小冈1， 陆敬辉1， 姜 伟1， 齐乃心1

(1. 火箭军工程大学 控制工程系， 陕西 西安 710025； 2. 火箭军工程大学 士官学院， 山东 青州 262500)

为提高复杂环境下红外小目标的检测率，提出了基于二阶方向导数极大值的红外小目标检测算法。该算法首先对二阶方向导数的性质进行了分析，对极大值进行阈值翻转操作，将背景中的平坦成分和边缘成分剔除。接着，根据小面模型对背景进行预测，并以预测误差为权值进一步增强小目标区域。以上2个步骤的计算可通过4个卷积实现，加快了检测速度。最后，对少量候选小目标计算局部对比度，降低了虚警率。实验结果表明：该检测算法在6种复杂背景下平均信杂比增益为78.413 0，平均背景抑制因子为35.079 6，具有较强的鲁棒性和较高的检测率。

机器视觉； 小面模型； 方向导数极大值； 红外小目标

2016-04-10；

2016-05-10

国家自然科学基金(61203189,61374054)资助项目

1000-7032(2016)09-1142-10

TP394.1 Document code： A

10.3788/fgxb20163709.1142