各向异性含水层水文地质参数的简化解析法

滕 凯

(黑龙江齐齐哈尔市齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)



各向异性含水层水文地质参数的简化解析法

滕 凯

(黑龙江齐齐哈尔市齐齐哈尔市水务局,黑龙江齐齐哈尔 161006)

摘要:针对各向异性含水层水文地质参数求解涉及多未知数超越方程,常规的解析法无法直接获解而现有的标准曲线比对法、直线图解法及改进直线解析法存在人为误差、适用范围受限或计算过程繁复等问题,采用优化拟合方法,在工程适用参数范围内,采用形式简单的函数替代用级数表示的井函数,并利用降深比值关系,在3个观测孔的水位降深曲线上选取6个点,经整理获得了可直接完成参数求解的简化计算公式,求解过程简捷直观,便于实际工程应用。精度分析表明,在工程适用参数范围内,该公式最大误差小于2%,满足实际工程的计算精度要求。

关键词:含水层;水文地质参数;水位降深;优化拟合;简化解析法

水文地质参数是开展地下水资源评价、制定地下水开采方案、实施地下水防污染计划的主要依据,一直以来备受水文地质工作者关注[1-2]。由于含水层形成条件的不均一性,使得自然界中地下水含水层水文地质参数在平面上往往存在较大的差异,完全均质各向同性的含水层几乎不存在,因此,采用在各向均质同性条件下建立的计算公式获得的水文参数存在误差[3]。为此,许多学者就平面各向异性含水层水文地质参数的求解问题开展了大量研究工作,并获得了有益的研究成果。目前应用的主要方法有曲线比对法[4]、Cooper-Jacob直线图解法[5]、改进直线解析法[6]及智能优化算法[7-10]。由于标准曲线比对法靠手动拟合,实际工作不但受图表束缚,而且求解成果因受标准曲线的密度及比对过程人为因素的影响,求解成果的精度难免存在误差[11],特别是当数据曲线比较平直时,拟合标准曲线的随意性更大;直线图解法仅当泰斯井函数的无量纲时间变量u≤0. 05,误差小于2. 1%时适用,应用范围有限,而且应用中要将适用范围以外的观测点剔除;改进直线解析法虽然适用范围有所扩大(u≤0. 3,误差小于2. 4%),但计算过程略显繁复,且适用范围仍显不足;智能优化算法由于涉及参数设定范围及初值选取、全局优化与局部优化的并行性、计算函数的梯度、收敛速度及迭代次数等复杂计算环境,实际应用尚存在不足。因此,研究提出一种计算方法简单、计算结果精度可靠的各向异性非稳定流情况下水文地质参数的获取方法,对进一步提高该种条件下水文地质参数的求解效率和精度具有重要意义。本文采用优化拟合方法,通过对泰斯井函数标准曲线的线型分析,借助现有表格给出的井函数数值对应关系,通过逐次逼近拟合计算,获得了泰斯井函数的简化替代公式,并利用该公式通过降深比值关系,经数学推导获得了通过选取3个观测孔抽水降深关系曲线上的6个点即可完成相关水文地质参数求解的计算公式,所得计算结果更接近工程实际,计算过程简捷直观,可在实际工程中推广应用。

1 理论分析

在无限延伸各向异性的承压含水层中,如一完整井以定流量Q进行连续抽水,其含水层中任意时刻任意一点的水位变化可用以下公式[12]表示:

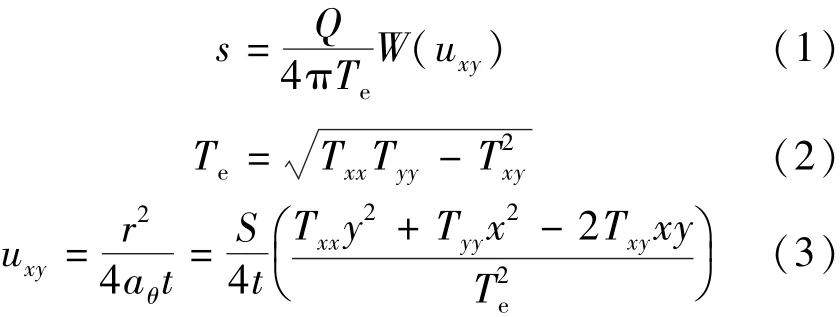
式中:s为任意时间、任意一点的水位降深,m;Q为抽水流量,m3/ h;Te为含水层的等效导水系数,m2/ h; W(uxy)为与泰斯公式形式相同的井函数;Txx、Tyy及Txy分别为导水系数在当地坐标系下的张量分量, m2/ h;x、y分别为当地坐标系的坐标分量,m;uxy为各向异性条件下泰斯井函数在当地坐标系下的无量纲时间;r为观测孔到抽水孔中心的径向距离,m; S为含水层弹性释水系数;aθ为与观测孔射线方向(与x轴夹角为θ)相一致的水压力传导系数,m2/ h; t为从开始抽水至抽水后任意时刻的时间,h。

根据式(3),在当地坐标系中,位置坐标为(xi, yi)的第i(i=1,2,3)个观测孔的无量纲时间可表示为

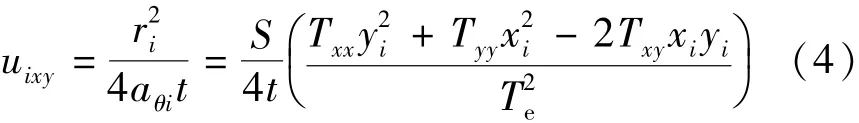
求得当地坐标系下导水系数的张量分量求得后,即可由下式获得在全局坐标系中导水系数的张量分量:

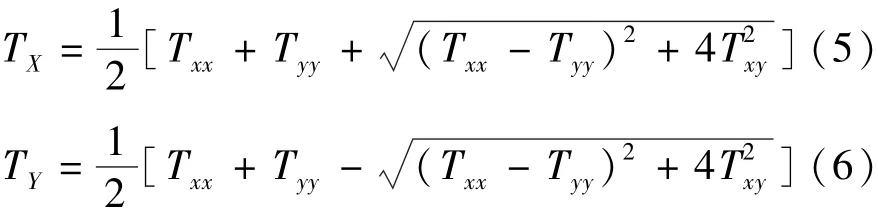
式中:TX、TY分别为导水系数在全局坐标系下的张量分量,m2/ h。

当地坐标系的x轴与全局坐标系的X轴间的夹角为

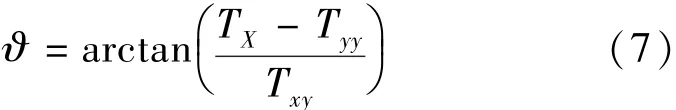
求得TX、TY后,全局坐标系中各向异性条件下的水头降深可表示为

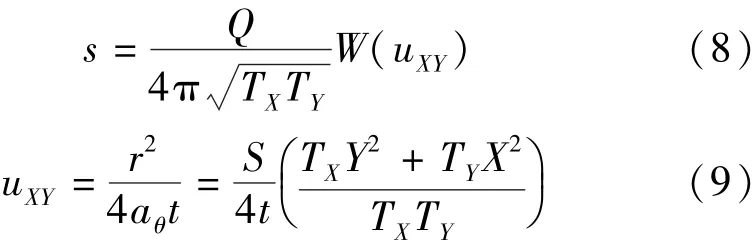
式中:uXY为全局坐标系下的无量纲时间;X、Y分别为全局坐标系下观测孔的位置坐标,m。

2 简化解析求解法

2. 1 井函数的简化

依据泰斯公式,井函数W(uxy)可表示为如下级数形式:

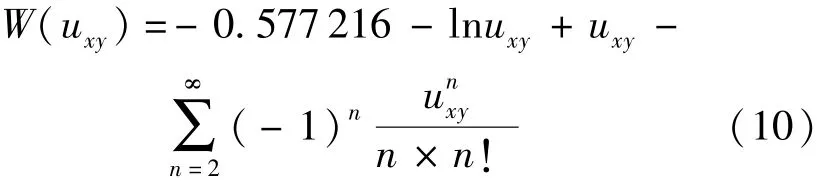
由于式(10)为超越方程,因此,利用式(1)无法直接求解相关参数。当uxy≤0. 05,误差小于2. 1% 时,Cooper-Jacob直线图解法截取了该级数的前2项;当uxy≤0. 3,误差小于2. 4%时,改进直线解析法截取了该级数的前3项。为进一步扩大公式的适用范围,本文采用优化拟合方法,以标准剩余差最小为目标函数[13],寻求一简化替代函数,并且满足:①替代函数中的变量可直接求得;②替代函数的表达形式相对简单;③替代函数具有较好的拟合精度,以保证求解方便且计算结果满足设计要求。在适用参数范围内(即1×10-7＜uxy＜6×10-1),经对多组备用函数的拟合逼近[14],择优确定式(10)的替代函数为

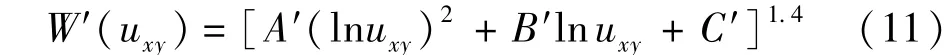
式中: A′= - 0. 009 812, B′= - 0. 572 445, C′= 0. 268954。

在1×10-7＜uxy＜6×10-1范围内,采用式(11)替代式(10)的计算误差见表1。由表1可见,在工程适用参数范围内(1×10-7＜uxy＜6×10-1),利用近似函数式(11)替代式(10)的最大误差小于2%,完全可以满足实际工程的设计精度要求(设计计算精度要求不大于5%)。

2. 2 简化计算公式

假设有一观测孔,其水位降深曲线为s-lgt,在s-lgt曲线上分别选取(t1,s1)和(t2,s2),则由式(1)可得到以下方程组:

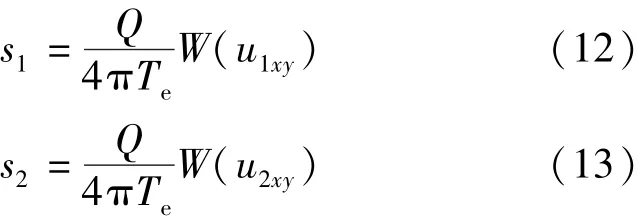
将方程(12)与(13)相比,并将式(11)及式(4)分别代入式(12)及(13),经进一步整理即可求得水压力传导系数aθ:

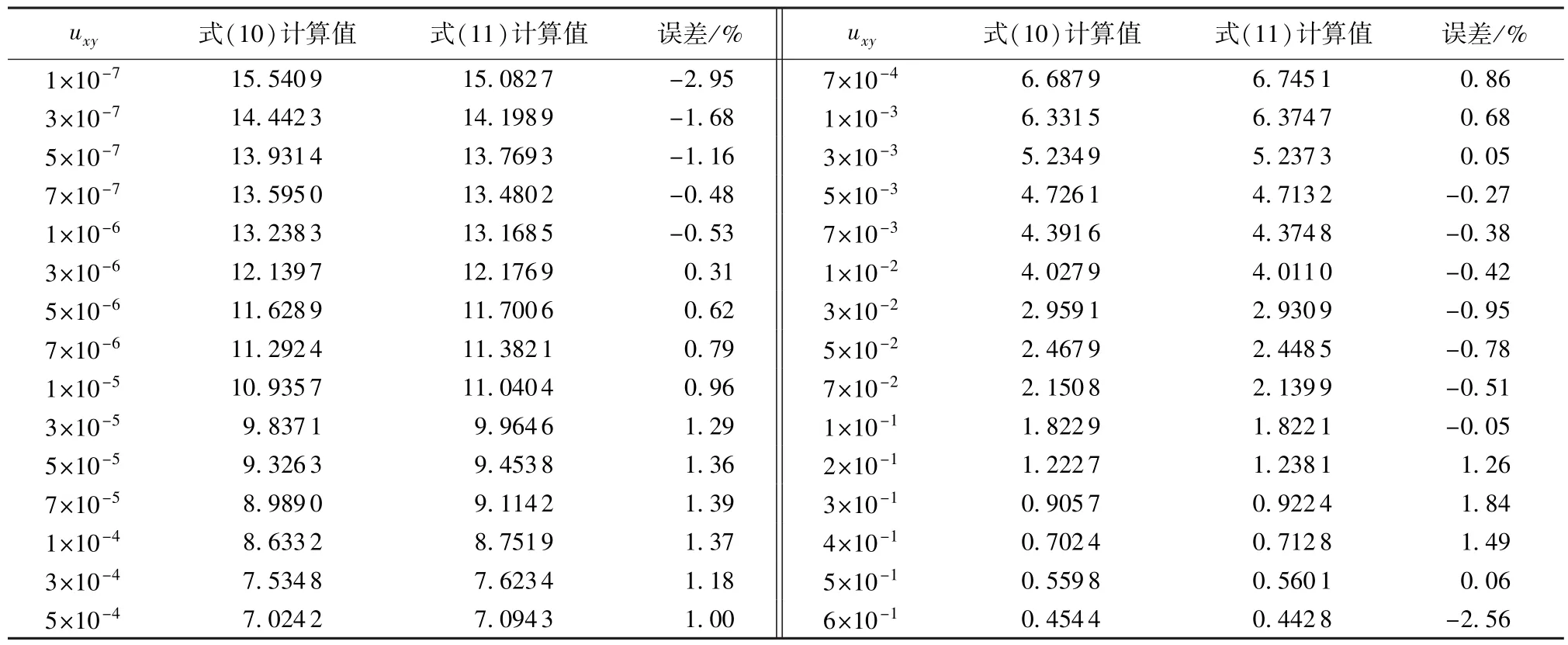
表1 式(11)相比式(10)的计算误差

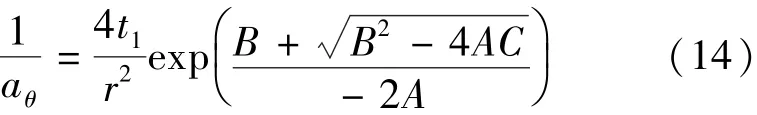
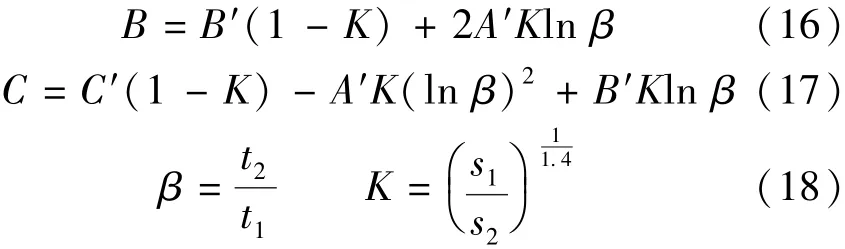
式中A、B、C、β及K均为中间变量。

当已知3个不在一条直线上的观测孔的降深-时间数据时,设第i个观测孔的降深-时间曲线为si-lgti(i为观测孔序号,i=1,2,3),距抽水井的径向距离为ri,(ti1,si1)和(ti2,si2)分别为在si-lgti曲线上选取的两个点,利用公式(18)可求得βi及Ki,再由式(15)(16)(17)分别求出Ai、Bi及Ci,进而可由式(14)求得aθi,则由式(1)(3)(11)可得Te:

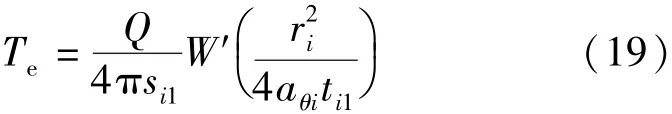
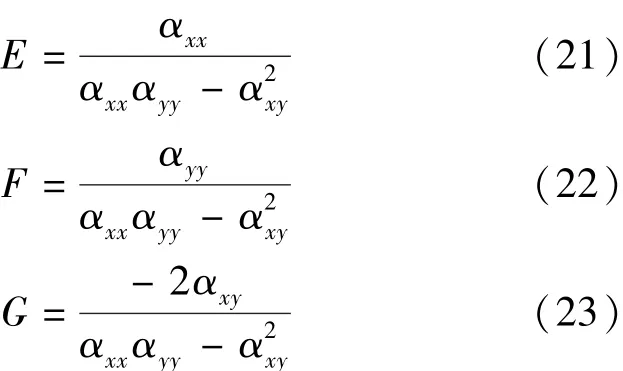
根据式(4)经进一步整理可得如下三元一次方程组:

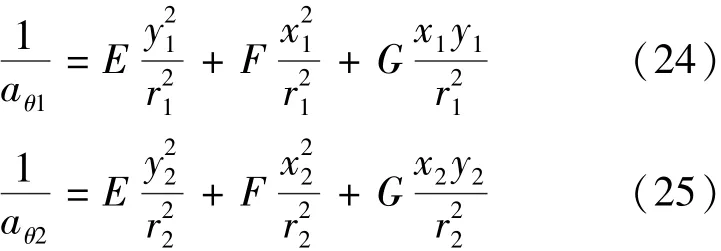
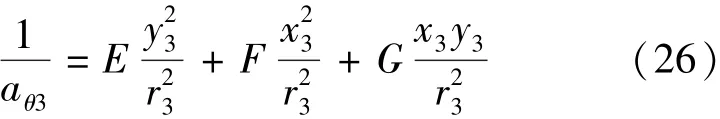
式中:αxx、αyy、αxy分别为水压力传导系数在当地坐标系的张量分量,m2/ h;E、F、G均为中间变量,h/ m2。求解方程组式(24)(25)(26)即可求得E、F及G,进而可得:

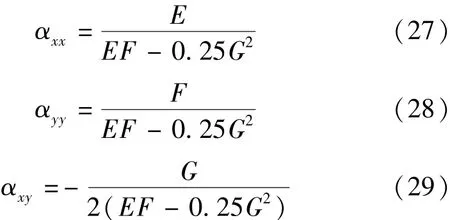
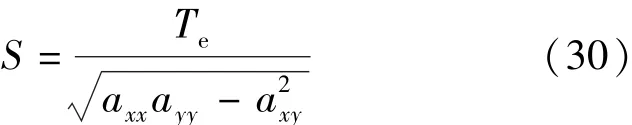
由式(20)(27)(28)(29)可求得Txx、Tyy及Txy,进而利用式(5)(6)(7)求得全局坐标系统下的张量分量TX、TY及夹角ϑ。

3 算例分析

选取文献[1]中算例,以抽水井所在位置为坐标原点,x轴正向为正东方向,y轴正向为正北方向。假定渗流主值与全局坐标不一致,在全局某正交各向异性含水层中,一完整井以定流量Q=1086 m3/ d进行非稳定流抽水试验,坐标系中有3个观测孔W1、W2和W3,其位置坐标分别为(28. 3,0)、(9. 0, 33. 5)和(-19. 3,-5. 2)。当抽水井抽水后,在3个观测孔中观测到的地下水降深随时间变化的实测数据如表2所示,试计算该含水层水文地质参数。

根据表2数据完成3个观测孔的si-lgti(i=1,2, 3)曲线绘制,并对曲线进行修正,剔除个别点因测量

或设备因素产生的误差影响,见图1,分别在各si-lgti关系曲线上选取两个点,即:t11=10 min,s11=1. 653 m; t12=300 min,s12=3. 351 m;t21=10 min,s21=1. 329 m; t22=300 min,s22=2. 998 m;t31=10 min,s31=1. 853 m; t32=300min,s32=3. 565 m。利用本文公式即可完成相关计算,中间变量及参数计算结果见表3,本文方法求解结果与文献[1]计算结果的比较见表4。

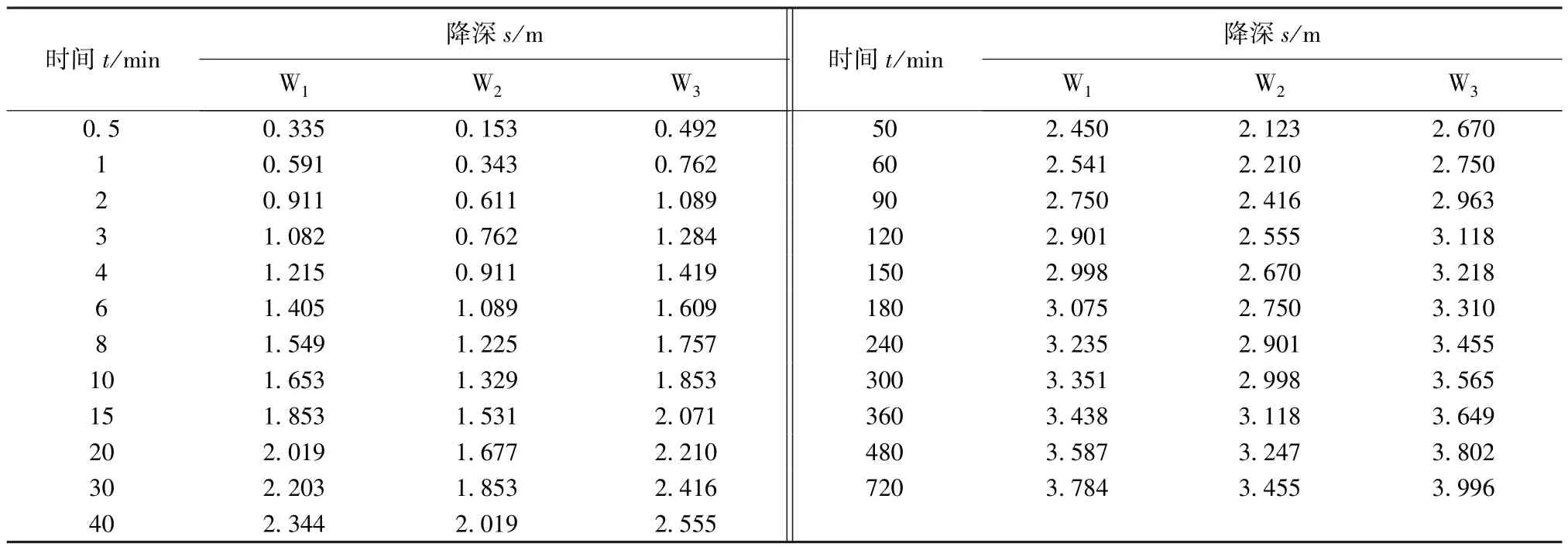
表2 各观测孔地下水降深实测资料

图1 s-lgt关系曲线

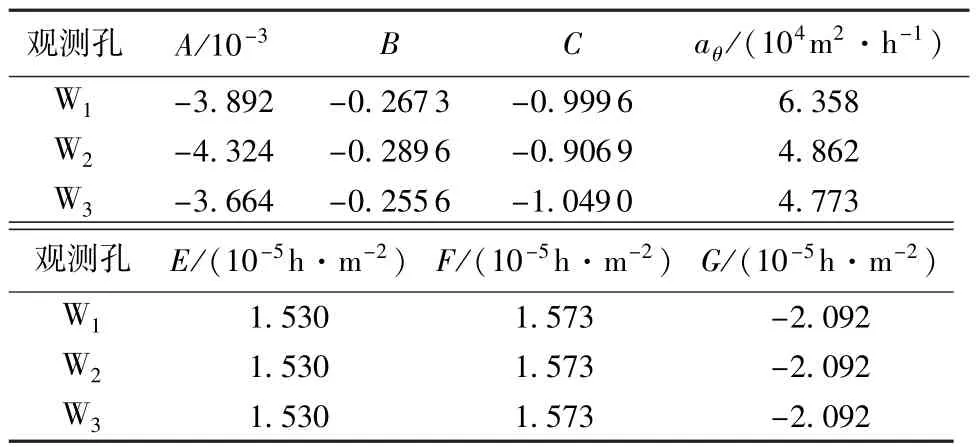
表3 中间变量及参数计算结果

表4 含水层参数计算成果

由表4可见,本文计算方法所求结果与文献[1]结果比较接近,其相对误差在-1. 89%～4. 54%之间(TX、TY、Txx、Tyy、Txy、Te、S的相对误差分别为2. 80%、-0. 44%、4. 54%、-0. 04%、3. 69%、1. 12% 和-1. 89%)。因此,认为本文方法具有较高的计算精度,可以满足实际工程的计算精度要求。

4 结 语

本文依据抽水降深比值关系,通过对各向异性含水层非稳定流井函数的优化拟合替代,方便快捷地完成了该种水文地质条件下参数的求解,与其他方法比较,具有以下特点:①公式形式比较简单,计算过程简捷直观。②求解不受图表束缚及标准曲线簇密度的影响,避免了图表取值的人为误差及反复进行拟合曲线比对的舍取之繁,便于推广应用。为有效提高计算结果的精度,考虑水位降深观测成果可能存在误差,计算前可根据观测孔的降深时间观测数据完成s-lgt曲线的绘制,并对s-lgt曲线进行修正,以便剔除个别点的观测误差影响。算例计算结果表明,本文公式在1×10-7＜uxy＜6×10-1范围内,替代函数与井函数的相对误差小于2%,计算精度较高。与其他方法比较,本文公式具有更好的实用性。

参考文献:

[ 1 ]洪昌红,邱静,黄本胜,等.补给带法在基岩裂隙水可开采量计算中的应用[J].水资源保护,2013,29(2):58-60. (HONG Changhong,QIU Jing,HUANG Bensheng,et al. Application of recharge zone method to calculation of allowable withdrawal of bedrock fissure water[J]. Water Resources Protection,2013,29(2):58-60. (in Chinese))

[ 2 ]孙才志,奚旭.不确定条件下的下辽河平原地下水本质脆弱性评价[J].水利水电科技进展,2014,34(5):1-7. (SUN Caizhi,XI Xu. Assessment of groundwater intrinsic vulnerability in the Lower Reaches of Liaohe River Plain under uncertain conditions[J]. Advances in Science and Technology of Water Resources,2014,34 (5):1-7. (in Chinese))

[ 3 ]刘燕,辛璐君,郭建青,等.抽水试验确定各向异性含水层参数的实例讨论[J].勘察科学技术,2012(6):5-9. (LIU Yan,XIN Lujun,GUO Jianqing,et al. Discussion of determining anisotropic aquifer parameters by pumping tests data[J]. Site Investigation Science and Technology, 2012(6):5-9. (in Chinese))

[ 4 ]《供水水文地质手册》编写组.供水水文地质手册[M].北京:地质出版社,1990.

[ 5 ]陈崇希,林敏.地下水动力学[M].武汉:中国地质大学出版社,1999.

[ 6 ]蒋名亮,韦佳,郭建青,等.改进直线解析法确定各向异性含水层参数的计算[J].中国农村水利水电,2014 (10):56-60. (JIANG Mingliang,WEI Jia,GUO Jianqing, et al. The calculation of anisotropy aquifer parameters by improved linear analytical method[J]. China Rural Water and Hydropower,2014(10):56-60. (in Chinese))

[ 7 ]高瑞忠,朝伦巴根,贾德彬,等.基于非稳定流抽水试验的BP神经网络确定含水层参数研究[J].沈阳农业大学学报,2004,35(6):510-512. (GAO Ruizhong,CHAO Lunbagen, JIA Debin, et al. Determining aquifer parameters with BP neural network based on unsteady flow pumping test [ J ]. Journal of Shenyang Agricultural University,2004,35(6):510-512. (in Chinese))

[ 8 ]魏连伟,邵景力,张建立,等.模拟退火算法反演水文地质参数算例研究[J].吉林大学学报(地球科学版), 2004,34 (4): 612-614. ( WEI Lianwei, SHAO Jingli, ZHANG Jianli,et al. Application of simulated annealing algorithm to hydrogeological parameter inversion [ J]. Journal of Jilin University(Earth Science Edition),2004, 34(4):612-614. (in Chinese))

[ 9 ]周秀秀,常安定,郭建青,等.混沌粒子群优化算法在确定含水层参数中的应用[J].水资源与水工程学报, 2013,24 (1):96-99. (ZHOU Xiuxiu,CHANG Anding, GUO Jianqing,et al. Application of chaos particle swarm optimization algorithms to estimation of aquifer parameters [J]. Journal of Water Resources and Water Engineering, 2013,24(1):96-99. (in Chinese))

[10]王媛英,刘元会,郭建青,等.差分-单纯形算法计算各向异性含水层参数[J].云南农业大学学报,2014,29 (4): 553-557. ( WANG Yuanyin, LIU Yuanhui, GUO Jianqing, et al. The estimation of anisotropic aquifer parameters by differential-simplex algorithm[J]. Journal of Yunnan Agricultural University,2014,29 (4):553-557. (in Chinese))

[11]李伟,赵燕容,朱旭芬,等.自动配线法求水文地质参数的优化路径法研究[J].勘察科学技术,2013(2):6-10. (LI Wei, ZHAO Yanrong, ZHU Xufen, et al. Study on optimization path method of solving hydrogeologic parameters by automatic curve-fitting method [ J]. Site Investigation Science and Technology,2013(2):6-10. (in Chinese))

[12] BATU V. Aquifer hydraulics:a comprehensive guide to hydrogeologic data analysis[M]. New York:John Wiley & Sons,1998:206-223.

[13]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.

[14]阎凤文.测量数据处理方法[M].北京:原子能出版社, 1988.

A simplified analytical method of hydrogeological parameters in anisotropic aquifer

/ / TENG Kai(Water Authority of Tsitsihar in Heilongjiang Proυince, Tsitsihar 161006, China)

Abstract:This study focuses on the transcendental equation with multiple unknowns for determining hydrogeological parameters in an anisotropic aquifer that cannot be directly determined through the conventional analytical methods. The existing methods for solving the equations, including the standard curve comparison method, linear graphic method, and improved linear analytical method, encounter many personal errors, a restricted application scope, and a burdensome and complicated computational process. In this study, adopting the optimum fitting method, a calculation formula for directly determining parameters was constructed using a simple function replacing the well function with a series expansion within the range of engineering adaptive parameters and a drawdown ratio relationship obtained through six selected points on the drawdown curves in three observation holes. The solution of the calculation formula is simple, intuitive, and easy to use. Precision analysis indicates that the maximum error is less than 2% across the range of engineering adaptive parameters, fully meeting the requirements of actual engineering calculation precision.

Key words:aquifer; hydrogeologic parameter; drawdown ratio; optimum fitting; simplified analytical method

(收稿日期:2015 01- 04 编辑:骆超)

作者简介:滕凯(1957—),男,高级工程师,主要从事水利防灾减灾及工程优化设计研究。E-mail:tengkai007@163. com

基金项目:齐齐哈尔市科技攻关项目(NYGG201301)

DOI:10. 3880/ j. issn. 1006- 7647. 2016. 02. 012

中图分类号:TV211. 12

文献标志码:A

文章编号:1006- 7647(2016)02- 0064- 05