完全规格化缔合勒让德函数及其导数的递推算法与适用范围比较

2016-04-11雷伟伟郑红晓

测绘工程 2016年6期

雷伟伟，郑红晓，李　凯

(1.河南理工大学测绘与国土信息工程学院，河南焦作 454000；2.河南省中纬测绘规划信息工程有限公司，河南焦作 454000；3.中国科学院上海天文台，上海 200030)

雷伟伟1，郑红晓2，李凯3

摘要：完全规格化缔合勒让德函数及其导数常用标准向前列递推算法和标准向前行递推算法进行计算。基于第一、第二相对数值精度标准对两种算法的适用范围进行分析比较，计算结果表明,标准向前列递推算法的适用范围大于标准向前行递推算法，说明前者优于后者；结果同时还表明，完全规格化缔合勒让德函数与其导数同一种算法的适用范围也相同，并指出了二者适用范围相同的原因。

关键词：完全规格化缔合勒让德函数；标准向前列递推算法；标准向前行递推算法；相对数值精度；适用范围

完全规格化缔合勒让德函数及其导数的计算是大地测量学、气象学、电子工程等多个学科领域的一个基本问题[1]。根据函数的基本定义公式直接进行展开计算的方法在计算效率和计算精度两个方面均不如递推计算方法，这种不足随着展开阶次的增大将更加明显。应用递推算法进行计算时首先需要考虑算法的适用范围，否则就会得到错误的计算结果。

国内外许多学者在递推算法方面也做了许多卓有成效的工作。文献[2]全面推导出了计算完全规格化缔合勒让德函数及其导数的标准向前列递推算法和标准向前行递推算法，为此后的相关研究奠定了基础；文献[3,4]表明标准向前列递推算法适用范围要大于标准向前行递推算法；而对两种算法适用范围的分析比较则主要由文献[5,6]完成，二者均选取了9个特定的数据对算法进行研究，验算数据不具备普遍的代表性。本文拟在上述研究基础上，从第一、第二相对数值精度两个方面，对递推算法的适用范围进行分析，以进一步详细明确它们的适用范围。

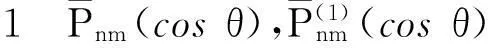
(1)

(2)

(3)

式(1～3)中:θ为球坐标系下的一个坐标量，θ∈[0°,180°]，在大地测量中称为天顶距，cosθ∈[-1,1]；n,m均为0或正整数，分别称为函数的阶、次，且n≥m。

(4)

1.1标准向前列递推算法

标准向前列递推算法计算公式为[2-3]

(5)

(6)

(7)

(8)

其中：式(5)中n≥2且n>m；式(6)中m≥2；式(7)中n>m；式(8)中m≥0。

在式(5～7)中：

递推初值为

(9)

上述递推算法结构设计如图1所示。

图1　标准向前列递推算法示意图

1.2标准向前行递推算法

标准向前行递推算法计算公式为[2-3]

(10)

(11)

式(10)中n≥2且n>m；式(11)中n>m。

在式(10～11)中：

此算法的递推初值也为式(9)。

上述递推算法结构设计如图2所示。

图2　标准向前行递推算法示意图

(12)

(13)

对于第n阶展开结果，记

(14)

(15)

在式(12)、式(14)中，cosθ∈[-1,1]，在式(13)、式(15)中，cosθ∈(-1,1)。

图3　第一相对数值精度与阶数之间的分布关系图(cos θ=0.9)

图4　第一相对数值精度与阶数之间的分布关系图(cos θ=0.999 9)

(16)

(17)

对于第N阶展开结果，记

NAN=

(18)

(19)

在式(16)、式(18)中，cosθ∈[-1,1]，在式(17)、式(19)中，cosθ∈(-1,1)。

图5　各种递推算法的适用范围分布示意图

3结论

参考文献：

[1]刘缵武，刘世晗，黄欧．超高阶次勒让德函数递推计算中的压缩因子和Horner求和技术[J]．测绘学报，2011，40(4)：454-458．

[2]COLOMBO O L.Numerical Methods for Harmonic Analysis on the Sphere[R].Rep 310,the Ohio State University,Columbus,Ohio,1981.

[3]HOLMES S A,FEATHERSTONE W E.A Unified Approach to the Clenshaw Summation and the Recursive Computation of Very High Degree and Order Normalized Associated Legendre Functions[J].Journal of Geodesy,2002,76(5):279-299.

[4]JEKELI C,LEE Jong Ki,KWON Jay H.On the Computation and Approximation of Ultra-high-degree Spherical Harmonic Series[J].Journal of Geodesy,2007,81(9):603-615.

[5]吴星，刘雁雨．多种超高阶次缔合勒让德函数计算方法的比较[J]．测绘科学技术学报，2006，23(3)：188-191．

[6]王建强，赵国强，朱广彬．常用超高阶次缔合勒让德函数计算方法对比分析[J]．大地测量与地球动力学，2009，29(2)：126-130．

[7]HOFMANN-wellenhof B,MORITZ H.Physical Geodesy (Second Corrected Edition)[M].New York：Springer Wien New York,2006.

[8]刘缵武，张敬伟，刘世晗，等．缔合勒让德函数的计算和球谐级数的截断误差分析[J]．海洋测绘，2012，32(3)：1-4．

[9]刘缵武，刘世晗，张敬伟．超高阶球谐级数式的计算方法[J]．数学的实践与认识，2012，42(9)：178-181．

[10] 张传定，许厚泽，吴星．地球重力场调合分析中的“轮胎”问题[C]//孙和平，熊熊，王勇.大地测量与地球动力学进展．武汉：湖北科学技术出版社，2004．

[11] 吴星，张传定．一类球谐函数与三角函数乘积积分的计算[J]．测绘科学，2004，29(6)：54-57.

[责任编辑：刘文霞]

Comparison of recursive algorithm and its applicable interval of fully normalized associated Legendre functions with their derivativeLEI Weiwei1，ZHENG Hongxiao2，LI Kai3

(1.School of Geodesy & Land information,Henan Polytechnic University,Jiaozuo 454000,China； 2.Henan Zhongwei Surveying and Planning Information Engineering Co.,Ltd.,Jiaozuo 454000,China； 3.Shanghai Astronomical Observatory,CAS,Shanghai 200030,China)

Abstract：The recursive algorithms including standard forward column algorithm and standard forward row algorithm are the common methods to calculate fully normalized associated Legendre functions and their derivative.In this paper,the applicable interval of these recursive algorithms is determined based on the first and second numerical accuracy of the algorithm.The results indicate the interval of standard forward column algorithm is bigger than standard forward row algorithm,so the former algorithm is better than the latter.It also indicates the applicable interval of the same algorithm of the fully normalized associated Legendre functions and their derivative are also the same,and the reasons of that are explained.

Key words：fully normalized associated Legendre functions;standard forward column algorithm;standard forward row algorithm;relative numerical accuracy;applicable interval.

中图分类号：P207

文献标识码：A

文章编号：1006-7949(2016)06-0001-05

作者简介：雷伟伟(1982-)，男，讲师，博士.

基金项目：国家自然科学基金资助项目(41172199，41474021)

收稿日期：2014-11-17