Levenberg-Marquardt算法在空间三维测边网中的应用
2016-04-11王罗刚王同合范百兴程志强王伟杰
王罗刚,王同合,范百兴,程志强,王伟杰
(1.信息工程大学,河南 郑州 450001;2.浙江华东建设工程有限公司,浙江 杭州 310000)
Levenberg-Marquardt算法在空间三维测边网中的应用
王罗刚1,王同合1,范百兴1,程志强1,王伟杰2
(1.信息工程大学,河南 郑州 450001;2.浙江华东建设工程有限公司,浙江 杭州 310000)
摘要:高精度三维坐标控制网是进行空间大尺寸精密坐标测量的基础,在对大尺寸机构和大型设备的安装、调试、监测过程中发挥着至关重要的作用。现阶段,激光测距的精度可达微米级,因此,利用激光测距可建立高精度的三维控制网。与边角网中点位精度受测角和测距精度两者的影响不同,三维测边网中点位精度仅受测距误差的影响。为了建立全局的精密三维控制网,文中基于激光测距建立了三维测边网整体平差模型,解算出测站点与定向点坐标,并利用Levenberg-Marquardt(LM)优化算法根据距离前方交会原理对三维网进行优化。经实验验证,优化算法提高了定向点的精度。
关键词:三维控制网;激光测距;Levenberg-Marquardt算法;距离前方交会
在精密工程测量领域,各种大型精密机械和实验设备安装工程的测量都离不开三维坐标控制网,例如大型飞机部件的装配、大型粒子加速器工程磁铁定位、大口径天线的安装、汽车船舶的制造等现代工业方面对测量精度提出了很高的要求[1,2]。激光跟踪仪采用单频激光干涉测距原理,可以获取极高精度的空间距离观测值,按球坐标原理求解出点位精度高达±(15 μm+6 μm/m),是当前精度最高的移动式坐标测量系统。利用激光跟踪仪建立大范围精密控制网已经取得了成功的运用,比如大型粒子加速器工程控制网、高速铁路轨道控制网(CPIII)等[3-6]。为充分发挥激光测距精度高的特点而又避免受到测角误差的影响,利用徕卡新型激光测距仪μ-base建立三维测边网,在自由网整体平差基础上,运用最Levenberg-Marquardt(LM)优化算法,对定向点的坐标进行优化,以提高定向点的精度。
1空间三维测边网
1.1μ-base测距仪
激光测距仪μ-base采用绝对距离测量技术(Absolute Distance Meter,ADM),基于斐索干涉原理(Fizeau’s principle),运用调制和偏振红外光,将周期性脉冲信号通过外部调制器叠加于红外光束,光束经过光电晶体时因为相对于光轴位置的不同(不同折射率) 导致线性偏振光具有不同的传播速度。通过调制频率获取整数级次N以及对应波长λ,即可计算出距离
(1)
测距仪μ-base由主机、电源适配器、接口盒及计算机等单元组成,如图1所示。
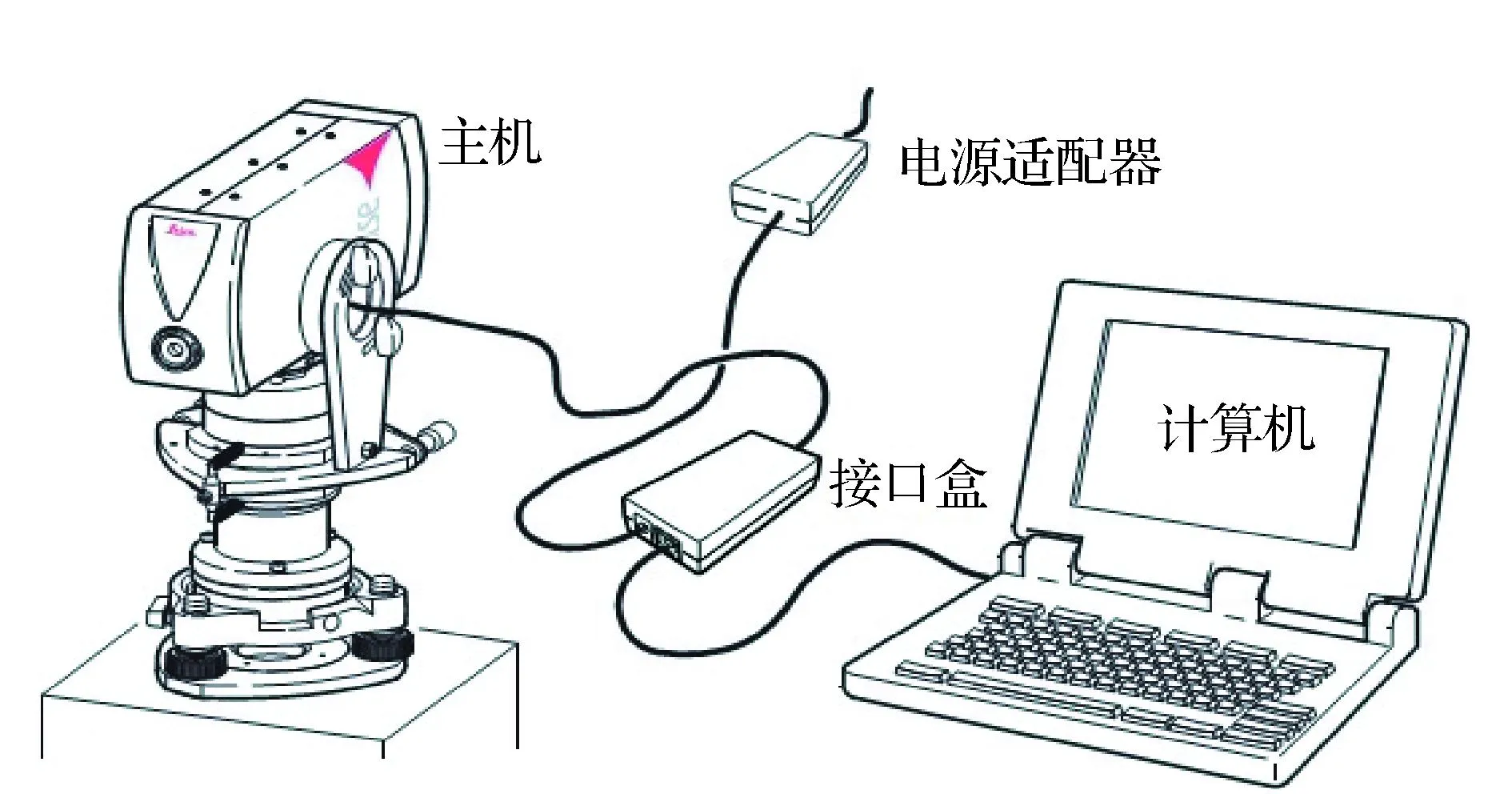
图1 μ-base测距仪
激光跟踪仪与μ-base测距仪的测距技术参数如表1所示。

表1 主要技术参数
徕卡新型激光测距仪μ-base在160 m测量范围内测距精度高达±10 μm,较之徕卡AT901-B型激光跟踪仪80 m量程有很大的优势,意味着可以减少仪器设站次数,减弱系统误差累积的影响。
1.2距离交会原理
在已知m个测站点对未知点P(x,y,z)进行距离测量得到S1,…,Sm,以各测站为中心,观测距离Si为半径,按两点间距离公式列方程组求出未知点P的坐标值,即为距离前方交会(见图2);反之,在未知测站测量已知坐标的定向点求解测站点坐标为距离后方交会[7]。在平面控制网中,至少需要2个测站才可交会求出点位平面坐标;空间三维控制网中,至少需要3个测站交会求出三维坐标值,多数情况下,常设3站以上保证有多余观测量求最优解。

图2 距离前方交会
从第i个测站观测未知点P,可得到该观测边Si的误差方程式
(2)
1.3控制网布设条件
布设独立测边网时,采用自由设站法,因此测站点坐标和定向点坐标都是未知的。在三维网中,无已知坐标、方位角和高度角作为基准则为自由网(无约束网)[8]。m个测站观测n个定向点产生mn个距离误差方程式,整个测边网中未知数只有测站点和定向点的三维坐标,不涉及各测站之间的旋转参数和尺度因子,因此,共有r=3(m+n)个未知数。要解算出整个控制网中全部未知数,测站数与定向点数需满足如下条件:

(3)
式中,m,n均取整数,测站数m与定向点数n进一步满足以下关系:
(4)
由上式可看出,不论测站增加多少,定向点数不能少于4个,两者最小取值对应关系如表2所示。

表2 测站数与定向点数关系
1.4整体平差方法
对式(2)距离观测方程进行线性化后得到误差方程
(5)

(6)
利用式(5)建立误差方程组
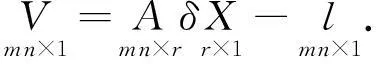
(7)
自由网平差中未知数向量只包括所有点的坐标未知数,没有固定基准引起基准秩亏,则在法方程矩阵N上加约束矩阵G消除奇异性并求出逆矩阵。通常三维网的基准数d=6,其矩阵中G满足NG=0,以重心为基准的约束矩阵G的具体形式有[9,10]
(8)

(9)
距离观测量互相独立且为同一仪器测量得到,权阵P取单位阵。
2Levenberg-Marquardt优化算法
三维网整体平差后可得到全部测站点和定向点的三维坐标,为提高定向点的点位精度,以测站点坐标为基准,按距离前方交会原理解算定向点坐标,列出观测距离残差方程
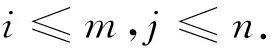
(10)
对于方程个数多于未知数的超定方程没有精确的求根公式,往往是在一定准则下优化逼近一组解作为最优值。
Levenberg Marquardt(列文伯格—马夸尔特法,LM)算法是广泛应用于各项领域的非线性最小二乘算法,可被看做是梯度下降法(gradient descent)和高斯牛顿法(Gauss-Newton)的组合,具备高斯牛顿法的局部收敛性和梯度下降法的全局特性[11,12]。
(11)
LM算法的基础是函数f在p附近的线性逼近,将f(p)进行泰勒一阶展开[13]
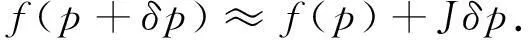
(12)

(13)
其标准最小二乘解为
(14)
当ε很小时,等式中法方程系数阵N=JTJ近似于Hessian矩阵,容易导致矩阵秩亏而无法求取N-1。LM算法对N进行改造,保持矩阵中非对角线元素不变,加入一对角阵μ(μ>0),得到新的法方程矩阵
(15)
在矩阵中加入对角阵的这种方法称为阻尼,μ为阻尼因子。将解算出的p+δp代入函数关系式,判断ε变化情况:若ε减小,则接受此μ并继续进行下一步迭代;若ε增大,则加大μ,直至ε减小。LM算法可自适应调整阻尼因子的大小,当收敛较慢时,增大μ,蜕化为梯度下降法;当收敛至最小值附近时,减小μ,更接近于高斯牛顿法。通过这种方式,得到δp的LM解
(16)
LM算法计算步骤如下:
1)给定初始参数向量p=p0并设定终止精度条件ε,计算εp=x-f(p)。k=0,μ=μ0,v>1。
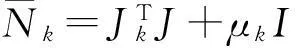

LM优化算法实质是通过采用系数矩阵阻尼的方法改造矩阵JTJ的性态,避免成为病态矩阵以此保证函数模型可解。算法的解算速度和精度主要取决于初始参数设置、算法参数及测量误差。
3实验与分析
3.1实验环境
在某室内实验场约15m×10m空间范围内,均匀布设16个定向点,分别固定于墙壁、地面和观测墩之上,最大高差约为1.5m;在场地中央分别布设4个测站,测距仪近似水平,且最大高差约为0.2m。点位平面分布情况如图3所示。

图3 控制网点位分布示意图
实验过程中,保持室内温度在25°左右,大气压强1 003.2kPa,湿度50%,最大限度减弱环境变化引起的测量误差。
3.2数据分析
采用自由网平差模型解算三维测边网,解算出测站点和定向点坐标的平差结果,分别如表3、表4所示。

表3 测站点坐标 mm
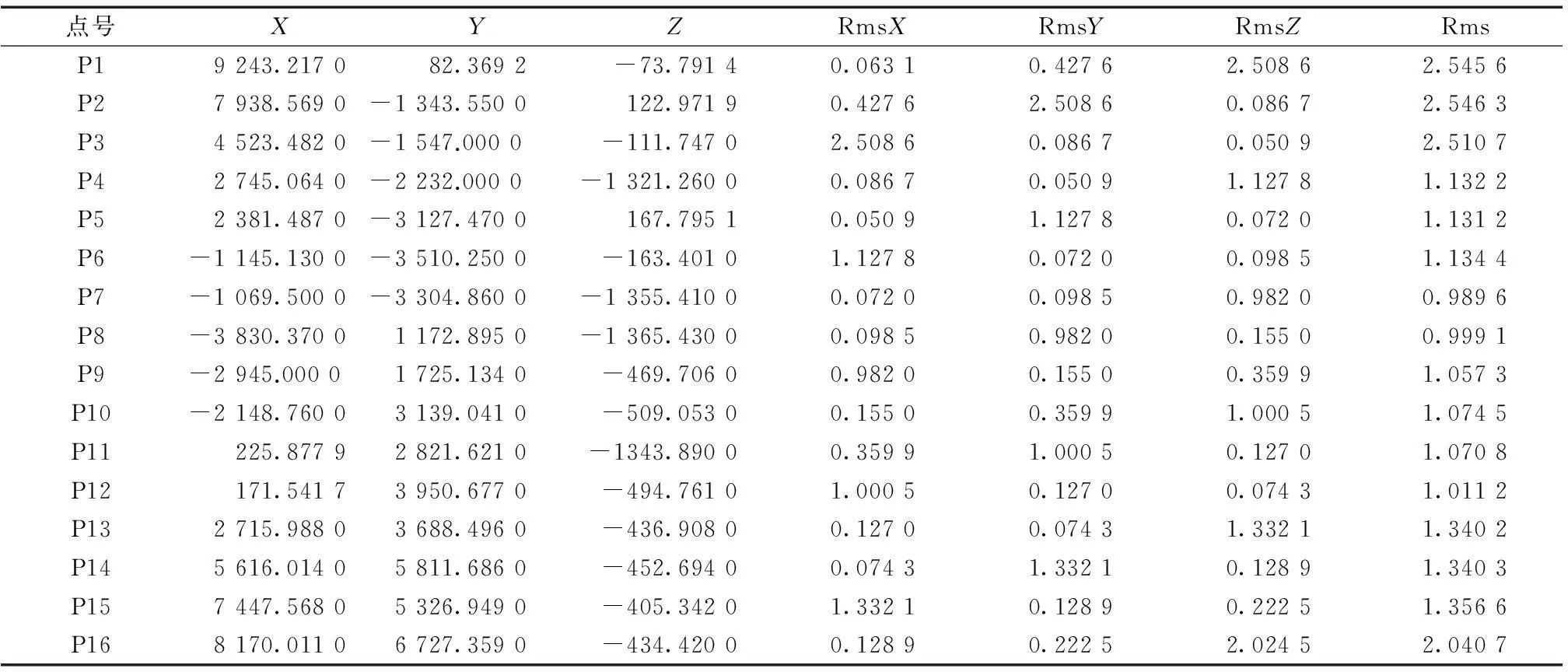
表4 定向点坐标 mm
从整网平差结果看,测站点坐标精度明显优于定向点坐标,但是z轴方向中误差远大于x轴和y轴;用平差结果反算各测站至定向点距离,误差平均值分别为2.8 μm,-2.8 μm,0.6 μm,1.5 μm。
3.3LM算法优化
采用LM优化算法对三维网整体平差后定向点的坐标进行优化,对比各点的平差与优化后坐标值中误差大小。定向点LM优化后效果如图4所示。

图4 定向点LM优化后效果
从图4中可以看出,经LM算法优化后x,y轴方向误差大幅下降且趋于平稳,点位的平面误差平均值由0.97 mm降至0.031 mm,垂直方向由0.65 mm降至0.02 mm。
4结论
1)LM优化算法充分利用激光测距精度高的优势,改善了整体平差结果,大幅提高了定向点的点位精度。
2)受实验场地的限制,点位布设在垂直方向最大相差1.5 m,网型结构较差导致三维网整体平差结果中z轴方向中误差偏大,下一步计划在更大空间范围内合理布置控制点,改善点位垂直方向的分布。
3)根据测站点与优化后的定向点坐标可反算出各个测站到定向点的距离,其与观测距离差值优于±20 μm。
参考文献:
[1]李广云,李宗春.工业测量系统原理与应用[M].北京:测绘出版社,2012.
[2]林嘉睿,邾继贵,郭寅,等.现场大空间测量中精密三维坐标控制网的建立[J].机械工程学报,2012,48(4):6-11.
[3]张三福.基于激光跟踪仪的精密控制网建立及其精度分析研究[D].兰州:兰州交通大学,2014.
[4]杨凡.高能粒子加速器工程精密测量研究[D].郑州:信息工程大学,2011.
[5]于成浩,柯明,赵振堂.激光跟踪仪测量精度的评定[J].测绘工程,2006,15(6):39-42.
[6]马洪磊,刘成龙,宋韬,等.自由测站方法在平面控制网测量中的应用[J].测绘工程,2014,23(5):51-54.
[7]孙乐.三边长后方交会在精密测量工程中的应用[J].西部交通科技,2014(20):155-160.
[8]张正禄.工程测量学[M].武汉:武汉大学出版社,2005.
[9]范百兴,李广云,李佩臻,等.激光干涉测距三维秩亏网的拟稳平差[J].测绘科学技术学报,2014(5):459-462.
[10] 范百兴,李广云,李佩臻,等.利用激光干涉测距三维网的加权秩亏自由网平差[J].武汉大学学报(信息科学版),2015,40(2):222-226.
[11] 张鸿燕,耿征.Levenberg-Marquardt算法的一种新解释[J].计算机工程与应用,2009,45(19):5-8.
[12] RANGANATHAN A.The Levenberg-Marquardt Algorithm[J].Tutoral on Lm Algorithm,2004,11(1):101-110.
[13] LOURAKIS M I A.A Brief Description of the Levenberg-Marquardt Algorithm Implemened by levmar[J].Foundation of Research & Technology,2005.
[责任编辑:刘文霞]
Application of Levenberg-Marquardt algorithm to 3D trilateration network
WANG Luogang1,WANG Tonghe1,FAN Baixing1,CHENG Zhiqiang1,WANG Weijie2
(1.Information Engineering University,Zhengzhou 450001,China;2.Zhejiang Huadong Construction Engineering Co.,Ltd,Hangzhou 310000,China)
Abstract:High precision three-dimensional coordinate control network is the basis of large space precision coordinate measuring,which plays a vital role in large institutions and equipment installation,debugging and monitoring process.At present,laser ranging accuracy can reach micron grade,so it can be used to establish a high precision three-dimensional control network.Different from the traditional triangulateration network,the control network is affected by the measurement accuracy and the accuracy of the distance measurement.The trilateration network is only related to the accuracy of the distance measurement.In order to build a global precision three-dimensional control network,this paper,based on the laser ranging established trilateration network overall adjustment model,consequently calculates the station and orientation points coordinates,and the Levenberg-Marquardt algorithm is used to optimized the network according to the distance forward intersection.The results show that the optimization algorithm can improve the accuracy of the orientation points.
Key words:three-dimensional network;laser ranging;Levenberg-Marquardt algorithm;distance forward intersection
中图分类号:P225
文献标识码:A
文章编号:1006-7949(2016)03-0068-05
作者简介:王罗刚(1991-),男,硕士研究生.
收稿日期:2015-07-21
