利用ARMA模型短期预报北极地区电离层TEC

卢建春，乔书波，冯　炜，祝海峰

(1.信息工程大学，河南 郑州 450001；2.中国科学院 测量与地球物理研究所，湖北 武汉 430077；3.北京卫星导航中心，北京 100094)



利用ARMA模型短期预报北极地区电离层TEC

卢建春1，乔书波1，冯炜2,3，祝海峰1

(1.信息工程大学，河南 郑州 450001；2.中国科学院 测量与地球物理研究所，湖北 武汉 430077；3.北京卫星导航中心，北京 100094)

摘要：北极地区电离层结构分布较为特殊，存在梯度变化。利用时间序列分析中的自回归移动平均模型(Autoregressive Moving Average，ARMA)对欧洲定轨中心(CODE)发布的北纬67.5°~87.5°以及利用反距离加权插值法得到的90°的格网数据逐点进行建模，分别利用7 d、10 d、20 d、30 d、40 d、50 d的电离层TEC值为样本数据采用线性最小方差法进行预报分析。结果表明：90%以上的预报绝对误差小于3 TECU，预报精度随TEC样本序列长度的增加而提高，但样本序列增加到一定值后，相对精度提高不大；相同样本数据的预报精度随预报时间长度的增加而降低，起初不是很明显，超过20 d后精度降低明显且波动幅度较大。尽管北极地区存在梯度变化，ARMA模型在北极地区具有较高的预报精度，是一种比较理想的预报方法。

关键词：ARMA；北极地区；电离层TEC；线性最小方差预报

电离层延迟是影响无线电信号传播的主要误差源之一[1]。电离层总电子含量(Total Electron Content,TEC)随着周日、季节、周年以及太阳活动周期的变化而变化，其变化对导航定位、远程通信、航空航天、天气预报等具有重要影响[2-4]。时间序列模型具有样本数据要求少、建模理论完善、计算过程相对简单、外延性好以及短期预报精度高等优势[5-6]。利用时间序列模型可以有效地对电离层TEC进行预报分析，许多学者做了大量的工作，文献[7-9]利用时间序列方法对IGS发布的电离层格网数据逐点进行建模预报，预报精度5 d内可达到80%左右。文献[10]提出了先用球谐函数模型拟合数据，然后对模型系数采用时间序列方法预报，最后由预报的系数求得相应的电离层预报值，减小了计算工作量。文献[11]利用改进的修正预测法，即用上一周期的预测误差改正修正预测法的结果，减小了极值点处的预测误差。文献[5]采用求和自回归移动平均模型，在充分考虑乘积性季节模型的情况下对电离层TEC时间序列进行了预报分析，达到较高的预报精度。文献[12]实现了基于轮胎调和分析的电离层TEC球谐系数模型并采用ARMA模型对球谐系数的时间序列进行了预报并获得了较高的预报精度等。

虽然很多学者利用时间序列模型预报分析电离层TEC取得了一定成果，但是由于北极地区电离层的特殊形态会导致TEC的显著波动[13]。常用的全球电离层改正模型在此地区的适应性较差，例如适用于单频接收机的Klobuchar模型[14]只能预报出一天内电子含量的50%～60%[15]，电离层活动剧烈的高纬度和低纬度地区，预报效果更差；球谐函数模型在北极地区适应性也较差，预报效果不理想等；而时间序列分析可以对一组有序数据进行观察、研究，找到它的变化发展规律，能够较好地预报其走势。基于此，本文利用CODE提供的电离层TEC数据，采用时间序列模型对北纬67.5°~87.5°以及利用反距离加权插值法得到的90°的电离层TEC进行了预报，同时对影响该方法预报精度的因素进行了分析。试验结果表明：90%以上的预报误差小于3 TECU；预报精度随着TEC样本序列长度的增加而提高，但样本序列增加到一定值后，相对精度提高不大；相同样本数据的预报精度随预报时间长度的增加而降低，起初不是很明显，超过20 d后精度降低明显且波动幅度较大。尽管北极地区存在梯度变化，ARMA模型在北极地区具有较高的预报精度，是一种比较理想的预报方法。

1ARMA模型

ARMA模型[16]是一种综合了自回归模型(Autoregressive,AR)和滑动平均模型(Moving Average,MA)的预报方法[17-18]。ARMA(p，q)模型的结构如下[19]：

(1)

其中:{xt}为时间序列过程；{εt}为白噪声序列；φ1，…，φp为自回归系数；θ1，…，θp为滑动平均系数[20]。

1.1模型识别及参数的确定

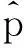
(2)

近似模型为

(3)

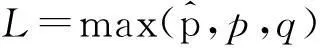
(4)

(5)

(6)

则目标函数可以写成

(7)

极小化目标函数后便可得到参数的最小二乘估计，其解为

(8)

白噪声方差的最小二乘估计为

(9)

然后根据白噪声方差分别计算不同(p,q)条件下的AIC或BIC值，取AIC或BIC达到最小时的(p,q)作为模型的阶数，对应的参数即为模型系数。

1.2时间序列法预报电离层TEC

预报是利用已观测到的样本值估算未来时刻的值，目前最常采用线性最小方差预报的方法预报平稳时间序列

(10)

式中，

(11)

2利用ARMA模型预报试验分析

CODE每2 h发布的电离层格网信息，包括经度方向间隔5°，纬度方向间隔2.5°共5 183个格网点的TEC数据。选取2011年年积日为161~167 d(7 d)、158~167 d(10 d)、148~167(20 d)、138~167(30 d)、128~167(40 d)、118~167 d(50 d)北纬67.5°~90°(其中90°的格网数据采用反距离加权插值法得到)的电离层格网数据逐点建立模型并进行预报分析，预报天数为7 d，用CODE发布的年积日为168~174 d的TEC值(作为真实值)与预报的电离层TEC作比较得到预报精度，为了考察预报结果的精度，笔者采用相对精度

(12)

式中:Ipre为预报的电离层TEC值；Icode为CODE发布的TEC值。

图1为第173号点样本序列的自相关和偏相关图，由图可知，该点样本序列的自相关、偏相关自始至终表现出很强的相关性，即拖尾现象，这与ARMA模型的特性相符合，所以采用ARMA建立预报模型(其它点类同)。

图1　第173号点样本序列的自相关与偏相关图

过高的阶数会使ARMA模型参数较多，降低模型的稳健性，且较多的参数会在很大程度上增加计算量[24]。考虑到模型的预报精度和工作量，作者将自回归阶数p和滑动平均阶数q的上限均取为12，ARMA模型采用使AIC达到最小的作为模型的阶数。

2.1所建ARMA模型性能分析

为了分析所建电离层TEC时间序列模型的整体性能，反演了2011年年积日为118~167 d中7 d、10 d、20 d、30 d、40 d、50 d等不同样本数据的时间序列，观察反演效果。图2是利用30 d的样本数据反演第2天的TEC值与实际观测值的绝对误差图。

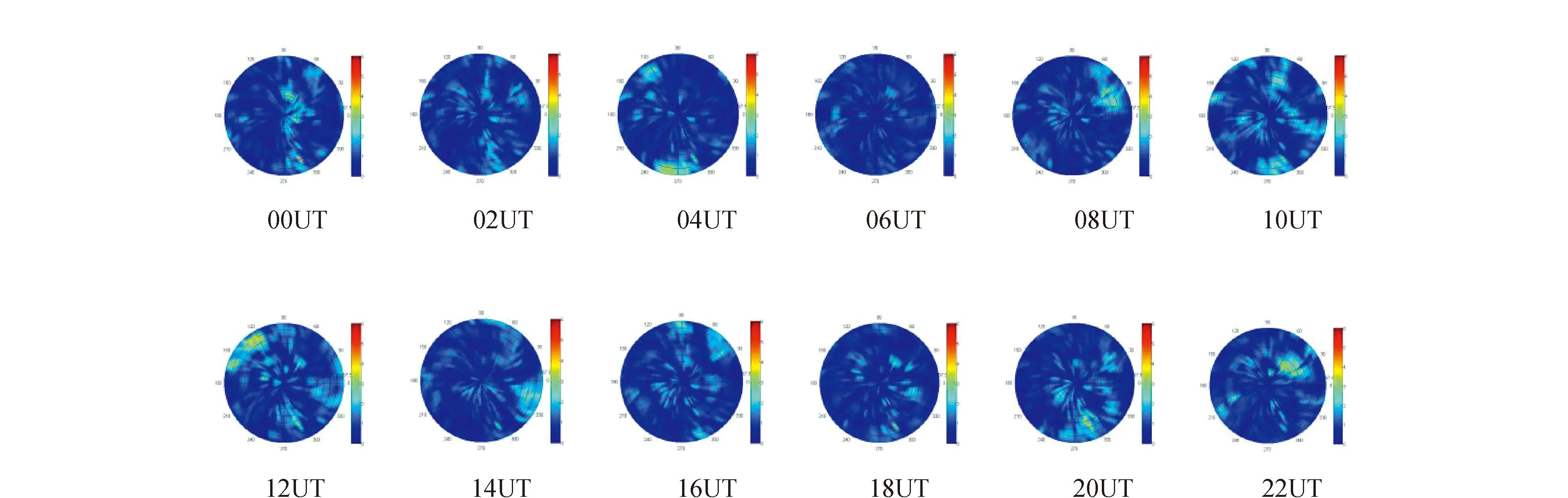
图2　反演电离层TEC的绝对误差值

图2是从北极进行方位投影的电离层TEC的极坐标图，图中以北极点为坐标原点，北极点与零度经线投影的连线构成X轴，坐标原点为90°，向外以2.5°递减直到67.5°，半径以90°为0向外以2.5递增，纬度为67.5°时半径为22.5。从图中可以看出，绝对误差基本都在1TECU以内，极个别点的绝对误差在2TECU左右，这些绝对误差表明构建的时间序列模型反演性能良好。

2.2北极地区电离层TEC预报

取2011年年积日为118~167 d CODE提供的北纬67.5°~87.5°以及采用反距离加权插值法得到的90°的格网TEC数据作为序列样本进行时间序列分析，采用7-7、10-7、20-7、30-7、40-7、50-7 6种模式对168~174 d的电离层TEC进行预报，研究了所采用样本数据的长短对预报结果的影响，同时分析了该方法所能达到的最大预报长度。限于篇幅，仅给出了样本数据长度为30 d的时间序列预报第1天的绝对误差图和实际观测图(见图3)。

图3　预报第1天的绝对误差图和实际观测图

图3中各图的原点、坐标轴、半径与图2相同。由图3分析可知，利用基于ARMA模型的时间序列分析法预报得到的TEC值与实际观测值符合的较好，在大多数情况下，预报绝对误差在3 TECU以内，与CODE本身提供的TEC值精度相当。对比图3(a)和图3(b)可以发现预报绝对误差相对较大的点正好对应于实测值较大的点。

表1为预报7 d预报绝对误差Δ的百分比统计，由统计结果可知，预报7 d时，有超过50%的数据预报绝对误差小于1 TECU；超过30%的数据预报绝对误差落在1~2 TECU区间内，90%以上的预报绝对误差小于3 TECU。尽管北极地区电离层变化迅速且构造特殊造成其存在梯度变化[13]，但从电离层TEC预报绝对误差的百分比统计可以看出，ARMA模型在北极地区具有较强的适应性，预报精度较高，是一种比较理想的预报方法。

表1　预报7 d预报绝对误差Δ(单位：TECU)的百分比统计

图4为采用上述6种预报模式的平均相对精度对比图。由图可知，样本序列长度在一定程度上影响预报精度，在最初阶段，随着样本序列长度的增加，预报精度有较明显的提高；样本序列增加到一定长度后变化不再明显，样本序列超过一定长度后，预报精度随着样本序列的增加开始下降。从图中可以看出，30 d左右的样本序列长度最佳，再增加样本序列长度对平均相对精度不会有明显的提高。

图4　6种预报模式的相对精度对比

图5为笔者取2011年年积日为118~124 d北纬67.5°~90°的电离层TEC作为样本数据向后预报50 d的平均相对精度图，由图可以看出，预报精度随预报时间的增加大致呈下降趋势，预报精度在前20 d左右平均相对精度在75%以上，且前10 d的平均相对精度在80%左右，超过20 d平均相对精度随时间的增加下降明显且波动幅度较大。

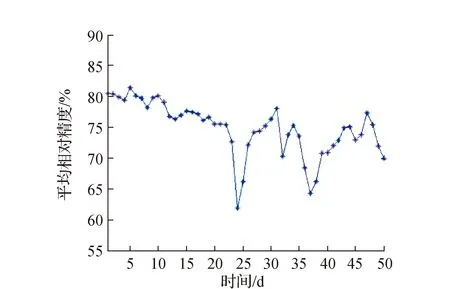
图5　预报50 d每天的平均相对精度统计

3结论

与中纬度地区不同，高纬度地区特别是极区上空的电离层变化规律不明显，存在电离层梯度变化，对其进行预报的难度较大，但是根据CODE发布的电离层格网数据，采用ARMA模型的预报结果较为理想，经大量试验分析，可以得到如下结论：

1)ARMA模型在北极地区预报电离层TEC是可行的，预报绝对误差小于1 TECU和落在1~2 TECU区间内的点占大多数，超过90%的绝对误差在3 TECU以内。

2)对于相同的预报时间长度，采用不同的样本数据长度具有不同的预报精度，规律是：预报所采用的样本数据长度能明显影响预报精度。在一定样本数据长度内，随着样本长度的增加，预报精度有较明显的提高，但样本超过一定长度后(30 d左右)，预报精度提高不大，随着样本数据长度的继续增加预报精度反而有所下降。

3)对于相同的样本数据，一般平均相对精度随预报时间的增加而降低，前20 d左右平均相对精度波动幅度较小，超过20 d后，平均相对精度随时间衰减明显且波动幅度较大。

参考文献：

[1]Acharya R，Roy B，Sivaraman M R，et al.Prediction of ionospheric total electron content using adaptive neural network with in-situ learning algorithm[J].Advances in Space Research，2011，47(1)：115-123.

[2]袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D].武汉：中国科学院测量与地球物理研究所，2002.

[3]孟泱，安家春，王泽民，等.基于GPS的南极电离层电子总含量空间分布特征研究[J].测绘学报，2011，40(1)：37-40.

[4]BHUYAN P K，BORAH R R.TEC Derived from GPS Network in India and Comparison with the IRI[J].Advances in Space Research，2007，39(5)：830-840.

[5]张小红，任晓东，吴风波，等.自回归移动平均模型的电离层总电子含量短期预报[J].测绘学报，2014，43(2)：118-124.

[6]ERDOGAN H，ARSLAN N.Identification of Vertical Total Electron Content by Time Series Analysis[J].Digital Signal Processing，2009，19(4)：740-749.

[7]武文俊，李志刚，杨旭海，等.利用时间序列模型预报电离层 TEC[J].时间频率学报，2008，31(2)：141-146.

[8]李志刚，程宗颐，冯初刚，等.电离层预报模型研究[J].地球物理学报，2007，50(2)：327-337.

[9]武文俊.电离层TEC预报模型研究[D].北京：中国科学院研究生院，2008.

[10] 李志刚，李伟超，程宗颐，等.电离层TEC预报的直接法和间接法及其比较[J].天文学报，2008，49(1)：29-44.

[11] 刘军，柴洪洲，常宜峰.改进的修正预测法预报电离层[J].测绘科学技术学报，2011，28(1)：19-22.

[12] 冯炜.电离层TEC的球谐函数分析与预报[D].郑州：信息工程大学，2014.

[13] 安家春，章迪，杜玉军，等.极区电离层梯度的特性分析[J].武汉大学学报(信息科学版)，2014，39(1)：75-79.

[14] KLOBUCHAR J A.Ionospheric time-delay algorithm for single-frequency GPS users[C].IEEE Transactions on Aerospace and electronics System AES，1986，23(3)：231-325.

[15] 阮仁桂，吴显平，冯来平，等．同时估计电离层延迟的单频精密单点定位方法[J]．测绘学报，2012，41(4)：490-495.

[16] BOX G E P,JENKINS G M.Time series analysis:Forecasting and control(revised edition)[M].Holden-Day，San Francisco，1976.

[17] 傅德印，刘晓梅.预测方法与应用[M].武汉：武汉大学出版社，2003.

[18] 陈军，李建文，李作虎.ARIMA模型在电离层TEC预报中的应用[J].测绘工程，2010，19(1):39-41.

[19] 王燕.应用时间序列分析[M].北京：中国人民大学出版社，2008.

[20] JAMES D H.Time Series Analysis[M].New Jersey：Princeton University Press，1994.

[21] 何书元.应用时间序列分析[M].北京：北京大学出版社，2007.

[22] AKAIKE H.Information theory and extension of the maximum likelihood principle[A].Eds B N Petroc and Caski F.In Second International Symposium in Information Theory[C].Budapest，Akademiai Kiado，1973，276-281.

[23] KAIKE H.On entropy maximization principle[A].Ed PR Krishnaiah.Applications of statistic[C].North Hollard，Amsterdam，1977，27-41.

[24] 刘军，柴洪洲，刘先东，等.基于ARIMA(p,1,1)的电离层预报模型[J].大地测量与地球动力学，2010，30(3)：79-82.

[责任编辑：刘文霞]

Short-term TEC prediction of the arctic ionosphere based on ARMA mode

lLU Jianchun1，QIAO Shubo1，FENG Wei2,3，ZHU Haifeng1

(1.Information Engineer University,Zhengzhou 450001，China；2.Institute of Geodesy and Geophysics,Chinese Academy of Sciences,Wuhan 430077，China；3.Beijing Application and Development Center of Round-the-World Information，Beijing 100094，China)

Abstract：The Arctic ionosphere structure distribution is special，which embraces the changes of gradient.The autoregressive moving average (ARMA) model is used from the time analysis theory to model the grid data of latitude 67.5°~87.5°provided by Center for Orbit Determination in Europe (CODE) and latitude 90° is obtained using Inverse Distance to a Power point by point.The ionosphere TEC of 7 days，10 days，20 days，30 days，40 days，50 days as sample data are adopted plus the linear minimum variance method for prediction.The results show that more than 90% of predicted absolute error is less than 3 TECU.The predicted accuracy will be improve with the increase of TEC sample sequences length，but it will gradually reduce if the length exceeds the optimal length about 40 days.On the other hand，with the same TEC sample，and the predicted days increase，the predicted accuracy decreases.Though it is not very obvious in the beginning，it will be reduced distinctly and the fluctuation will be larger over 20 days.Despite the existence of change of gradient in the Arctic，the ARMA model has good predicted accuracy,which will be a kind of ideal predicted model.

Key words：ARMA；Arctic；ionosphere TEC；linear minimum variance prediction

中图分类号：P228

文献标识码：A

文章编号：1006-7949(2016)03-0030-05

作者简介：卢建春(1989-)，男，硕士研究生.

基金项目：国家自然科学基金资助项目(U1431115；41374042)；大地测量与地球动力学国家实验室开放式基金资助项目(SKLGED 2014-3-5-E)

收稿日期：2015-06-15