一种快速二维Delaunay三角网点定位算法

王　雯，吴　蔚，苏天赟

(1.中国海洋大学 信息科学与工程学院，山东 青岛 266100；2.国家海洋局第一海洋研究所，山东 青岛 266061)



一种快速二维Delaunay三角网点定位算法

王雯1，吴蔚1，苏天赟2

(1.中国海洋大学 信息科学与工程学院，山东 青岛 266100；2.国家海洋局第一海洋研究所，山东 青岛 266061)

摘要：在构建二维Delaunay三角网的逐点插入法中，定位待插点所在三角形的快慢是影响整个算法构网速度的关键因素。针对目前已有算法存在的搜索路径长、搜索路径求解计算量大等问题，结合三角形重心的几何性质，对点定位算法进行改进，避免求三角形重心和相交边的过程。实验结果表明，文中算法较目前其他点定位算法能够有效地缩短搜索路径，减少点定位的计算时间，提高Delaunay三角网构网过程中点定位的效率。

关键词：Delaunay三角网；逐点插入法；点定位算法；三角形重心

三角剖分是计算几何领域的重要研究内容之一，而其中Delaunay三角剖分由于具有许多优良性质，在地理信息系统、数字高程插值、有限元分析、几何重构等领域有着广泛的应用[1-2]。目前构建Delaunay三角网应用最多的方法是逐点插入法，而确定包含待插点的三角形(目标三角形)是逐点插入法中的一个重要步骤，一般将其称为点定位问题。通过改进点定位算法，可以有效提高Delaunay三角网构建效率。刘学军等提出了一种基于面积坐标的点定位算法，利用建立的三角形间的拓扑关系和三角形面积坐标判断定位，这种方法的计算效率高，但是由于搜索路径不唯一，造成了搜索路径中很多不必要的“绕弯”现象，增加了判断三角形的个数[3]。刘少华等利用点和有向线段的正负划分来定位,该方法的本质与面积坐标法相同，计算效率高,但搜索路径同样不唯一[4]。宋占峰等提出最速方向定位法，通过将第一个要搜索的三角形重心指向待插点的连线作为方向线，如果点不在三角形内，则与方向线相交的边相邻的三角形就为下一搜索三角形，该方法计算效率较低，但搜索路径唯一[5]。蒲浩等提出重心方向搜索法，通过判断当前三角形的重心点和待插点相对于三角形三条边的关系来定位，虽然搜索路径是目前几种算法中最短的，但计算效率也最低[6]。张咏等提出点定位融和算法，将文献[3]与文献[6]的方法相结合，先用面积坐标法判断搜索路径，当遇到结果不唯一的情况时，将当前判断的三角形重心与待插点相连，连线经过的与当前判断三角形相邻的三角形即为下一个要判断的三角形[7]。这种方法的搜索路径与文献[6]相同，但用面积坐标法判断结果不唯一时，还是要计算三角形重心和判断连线经过的三角形，计算效率仍有待提升。

本文针对以上算法的不足，对点定位算法进行了改进，当遇到不确定的情形时，利用三角形重心的性质和点与三角形三边位置关系的计算结果，可以快速判断出重心与待插点连线经过的相邻三角形，计算效率得到了提高，搜索路径与文献[6-7]相同且为目前方法中的最短路径。

1算法概述

在构建Delaunay三角网的3种主要方法中，与分治算法、三角网生长法相比，逐点插入法具有算法简单、占用空间小、便于动态更新等优点。其主要流程如下：

1)先构建包围所有点集的初始矩形凸壳并连接一条对角线形成初始三角网；

2)将点集中的点按照一定的规律进行排序，依次插入到三角网中；

3)对于每一个待插点，首先要找到待插点所在的三角形，然后从这个三角形开始对其每一条边的邻接三角形进行外接圆检测，进而得到包含当前待插点所有影响域的空腔，再将待插点与空腔顶点相连并更新三角形的邻接关系即完成了一个待插点的插入；

4)将所有点插入完毕后，删除与初始矩形凸壳4个顶点相连的辅助三角形，即完成了Delaunay三角网的构建。

逐点插入法的流程如图1所示。

图1　逐点插入法流程

在逐点插入法的Delaunay构网过程中，对于每一个待插点都首先要进行点定位过程，即定位该点所在三角形，只有正确找到待插点所在三角形才能进行建立空腔和三角网更新。点定位算法的主要思想是先确定第一个要搜索的三角形(首三角形)，然后利用数学方法判断点是否在三角形中。如果不在，则利用待插点和这个三角形的位置关系，找到下一个要判断的三角形。在这个过程中，要判断的三角形会逐渐与待插点靠近，直到找到目标三角形。这些判断过的三角形会形成一条路径，称为搜索路径。点定位算法的效率主要受以下3个因素影响：

Factor1：首三角形与待插点所在三角形的距离；

Factor2：搜索路径中三角形的数量；

Factor3：判断点与三角形位置关系时的计算公式的复杂度。

对于Factor1可以采用分块建立局部三角形区域索引，或者把前一个待插点最后一个更新的三角形作为首三角形的方法。由于选取首三角形的方法主要取决于逐点插入法中点的插入顺序，本文对此不作重点阐述。对于Factor2，如果选择的搜索路径中三角形数量较多会增加点与三角形关系的判断次数；对于Factor3，如果判断点和三角形位置关系时采用复杂的计算方法，会使待插点与每个三角形的判断的时间增加。这些都会对逐点插入法的整体效率产生很大影响。因此，简化点定位过程，减少点定位过程中对点和边关系的判断次数和计算复杂度，对提高整体Delaunay的构网效率有着重要作用。本文重点针对Factor2和Factor3两个因子，对点定位算法进行改进，以提高Delaunay构网效率。

2算法改进

2.1分区原则

从定位角度考虑，可以把三角形所在平面分成三大区域。Ⅰ区为三角形所在区域；Ⅱ区为三角形任意一边和另两边延长线组成区域；Ⅲ区为任意两条边的延长线交叉组成区域。待插点与当前判断三角形的位置关系可以通过待插点与三角形任意两顶点形成新三角形的面积正负来确定[8]。如图2所示，设平面任意△ABC，其3个顶点按照逆时针顺序编号，坐标分别为A(xa,ya)，B(xb,yb)，C(xc,yc)；对任意点P(xp,yp)，P与三角形三边AB，BC，CA构成的三角形面积分别为SA，SB，SC，称边AB，BC，CA分别为SA，SB，SC的对应边，则

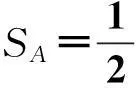
(1)

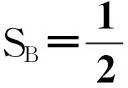
(2)

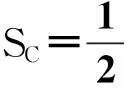
(3)

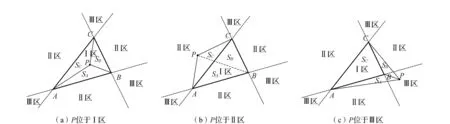
图2　点P位于不同区域的示意图

当SA，SB，SC均大于等于0时，P位于△ABC内或其边上，即为Ⅰ区，如图2(a)所示；当SA，SB，SC有一个小于0时，P位于相应的小于0的S对应边的外侧，即为Ⅱ区，如图2(b)所示；当SA，SB，SC有两个小于0时，P点位于相应的小于0的S对应的两条边的外侧，即为Ⅲ区，如图2(c)所示。其中将点在三角形边上的情况归于Ⅰ区是为了避免在三角形边上的点无法属于任何三角形的情况；将待插点在三角形三边延长线的情况归于Ⅱ区是因为点在Ⅲ区的处理方式比Ⅱ区复杂，这样可以简化计算。

2.2路径判断

2.2.1判断方法

对于待插点位于Ⅰ区和Ⅱ区的情况，面积坐标法可以很快找到最短路径中下一个判断的三角形。而对于待插点位于Ⅲ区的情况，目前的点定位算法文献[3-7]的判断处理方法各有不同，这些算法有些会增加Factor2中的三角形数量，有些需要求三角形重心坐标和相交边，从而增加Factor3中的计算公式复杂度。本文通过对点定位算法的影响因素的分析，对点位于Ⅲ区时的处理过程进行了优化。

针对Factor2，文献[7]已证明其算法的搜索路径是目前已有算法中的最短路径。根据文献[7]中所述，当待插点位于当前判断三角形的Ⅲ区时，将当前判断三角形的重心与待插点相连，判断与连线相交的是三角形的哪条边，则下一个要判断的三角形就是该边的临边三角形。本文算法采用与文献[7]相同的搜索路径，即目前算法中的最短路径。

针对Factor3，当待插点位于Ⅲ区时，文献[5-7]都无法避免求三角形重心坐标和相交边的过程，每判断一个三角形就要进行重心坐标计算和多次直线方程求交计算，影响点定位算法的计算效率。本文提出了一种简化的判别准则，即：

当待插点位于Ⅲ区时，SA，SB，SC中，最小的S所对应的边即为当前判断三角形的重心与待插点连线穿过的边。

采用这种判别准则，可以有效避免求三角形重心和相交边的过程，从而可以提高待插点位于Ⅲ区时定位三角形的计算效率。

2.2.2方法证明

算法示意图如图3所示。

图3(a)所示，设△ABC为当前判断的三角形，P′是位于Ⅲ区的待插点。分别将△ABC的3个顶点C，A，B与对边中点M1，M2，M3相连，由三角形重心定义可知CM1，AM2，BM3相交于一点即为重心G。将线GB沿GB方向延长，延长线将边AB，CB延长线交叉形成的Ⅲ区分成a，b两个区域。首先假设P′位于a区，过P′分别向AB和CB延长线做垂线，垂足分别为D和E′。将直线DP′沿DP′方向延长交GB延长线于P。过P向CB延长线作垂线，垂足为E。过G分别向AB和BC作垂线，垂足分别为F和H。则由三角形中线的性质可知,△ABC和△APC被各自中线BM3和PM3分得的三角形面积相等，进而可以得到S△ABP=S△CBP，即

图3　算法示意图

(4)

由于点P′位于a区，DP′长度一定小于DP。将图3(a)中的四边形BDPE放大，放大后如图3(b)所示，过P′作P′D′平行PB交BD与D′，过D′向P′E′作垂线，垂足为I。可知△BEP∽△D′IP′，△BDP∽△D′DP′，进而得到

由图中可知P′I长度一定小于P′E′，则

(5)

(6)

由于待插点在由AB，CB延长线组成的Ⅲ区时必有SA<0，SB<0，SC>0，最小值一定在SA，SB中。进而可以由式(6)得到SB为最小值。所以当待插点位于a区时，下一个要判断的三角形为最小值SB对应的BC边的临边三角形，此时GP′一定与边BC相交。

同理可证，当待插点位于b区时最小值SA，则下一个要判断的三角形为SA对应的AB边的临边三角形，此时GP′一定与边AB相交，与求重心坐标和求相交边的方法得到的结果一致。

因此，本文提出的判别准则可以取代求重心坐标和相交边的过程，用于待插点位于Ⅲ区时定位三角形的计算。这样，本文算法既满足了最短搜索路径，又简化了定位三角形的计算和判断过程，使得整个点定位算法的计算效率得到了有效的提升。

2.3实现步骤

设待插点为P(xp,yp)，*pTri为当前判断的三角形指针，*pTri当前指向△ABC，三顶点ABC逆时针排列，坐标分别为A(xa,ya)，B(xb,yb)，C(xc,yc)，则算法的具体步骤如下：

Step1：将首三角形作为当前判断三角形，即将*pTri指向首三角形；

Step2：创建双精度型数组s[3]、整型变量negativenum并赋值为0；

Step3：用式(1)、(2)、(3)求出s[0]=SA，s[1]=SB,s[2]=SC的值，且每当s[i]<0时(i=0,1,2)，negativenum自加1；

Step4：若negativenum=0，则当前判断的三角形即为点P所在三角形，算法结束，否则进行Step5；

Step5：若negativenum=1，则将相应小于0的s[i]所对应的边(s[0]对应AB边，s[1]对应BC边，s[2]对应CA边)的临边三角形作为下一个要判断的三角形，并将*pTri指向该三角形，negativenum清零，执行Step3，否则执行Step6；

Step6：若negativenum=2，则比较s[0]、s[1]、s[2]的大小，将其中最小的s[i]所对应的边的临边三角形作为下一个要判断的三角形，并将*pTri指向该三角形，negativenum清零，执行Step3。

3实验结果及分析

为了测试本文算法的效率，基于点插入顺序为随机排列的逐点插入构网方法对面积坐标法[3]、重心方向搜索法[5]、最速方向定位法[6]、点定位融和法[7]以及本文算法进行了测试，测试环境为Intel(R) Core(TM)2 Duo CPU T6670 @ 2.20GHz，4GB内存，win7，64位操作系统，测试点集为点数为1 000万的均匀分布的点集。经测试，这5种算法的时间复杂度均为O(N)。为使测试结果更加直观，引入平均每个待插点搜索路径中的三角形个数(NP)，NP值越小搜索路径越短。各种方法中每个待插点的首三角形都是相同的，选取规则都是把前一个插入点最后一个更新的三角形作为首三角形。测试结果如表1所示。

表1　不同算法效率对比

从表中可以看出，对于搜索路径，重心方向搜索法、点定位融和法和本文算法的NP值相同且为最小，因为这3种方法的搜索路径相同且是这几种方法中最短的；相比这3种算法，最速方向定位法的搜索路径略长，所以NP值也略高；面积坐标法由于搜索路径中很多绕弯现象的存在，NP值最高。对于算法效率，面积坐标法由于无需求重心坐标和相交边，虽然判断的三角形最多(NP值最大)但算法效率依旧很高；而重心方向搜索法对于每个判断三角形都要求重心坐标和相交边，虽然搜索路径最短但算法效率最低，搜索时间约为面积坐标法的2倍；最速方向定位法将重心方向搜索法中对每个三角形重心坐标的计算简化为只求首三角形的重心坐标，所以搜索时间比重心方向搜索法略少，但依旧比面积坐标法多出约60%的搜索时间；点定位融和法将面积坐标法和重心方向搜索法结合，搜索时间比重心方向搜索法降低了约10%；而本文算法由于搜索路径最短，计算效率与面积坐标法相当，所以最终算法效率是5种方法中最高的。

4结束语

本文在现有点定位算法基础上，结合三角形重心的几何性质，提出了一种新的点定位算法，对点定位算法中待插点位于三角形两条边外侧时的计算效率进行了优化，避免了求三角形重心和相交边的过程。测试结果表明，本文算法不仅搜索路径短，而且算法效率高，可以有效地提升Delaunay构网算法的效率，具有一定的应用价值。

参考文献：

[1]谢增广.平面点集Delaunay三角剖分的分治算法[J].计算机工程与设计，2012，33(1)：2652-2658.

[2]李小秋，许民献，尹志永.Delaunay三角网关键技术探讨[J].测绘工程，2011，20(6)：61-67.

[3]刘学军，符锌砂，赵建三.三角网数字地面模型快速构建算法研究[J].中国公路学报，2000，13(2)：31-36.

[4]刘少华，吴东胜，罗小龙，等.Delaunay三角网中点目标快速定位算法研究[J].测绘科学，2007，32(2)：69-71.

[5]宋占峰，蒲浩，詹振炎.基于三角网数字地面模型快速定位算法的研究[J].中国铁道科学，2002，23(1)：63-66.

[6]蒲浩，宋占峰，詹振炎.快速构建三角网数字地面模型方法的研究[J].中国铁道科学，2001，22(6)：100-105.

[7]张咏，刘长星，杨瑜华，等.基于融合算法的二维Delaunay三角网任意点定位研究[J].测绘科学，2010，35(2)：84-87.

[8]JOHN B M.Transformation of trilinear and quadriplanar coordinates to and from cartesian coordinates[J].American Mineralogist,1964,49(7,8)：926-936.

[责任编辑：刘文霞]

A rapid algorithm for point positioning in 2D delaunay triangulation

WANG Wen1,WU Wei1,SU Tianyun2

(1.School of Information Science and Engineering,Ocean University of China,Qingdao 266100,China；2.State Oceanic Administration,First Institute of Oceanography,Qingdao 266061,China)

Abstract：In incremental insertion algorithms of 2D Delaunay triangulation,seeking out the triangle which the inserting point locates in is the key factor influencing the efficiency.In this paper,point positioning algorithm is improved by avoiding the calculation of gravity center and intersecting edge,which makes the use of geometric properties for triangle barycenter to solve the problem that searching path is too long and complicated to calculate in present algorithms.The experimental results show the algorithm in this paper can shorten the searching path and reduce the time of point positioning process,ultimately improve the efficiency of delaunay triangulation compared with other present point positioning algorithms.

Key words：delaunay triangulation；incremental insertion algorithm；point positioning algorithm；triangle barycenter

中图分类号：TP391

文献标识码：A

文章编号：1006-7949(2016)03-0025-05

作者简介：王雯(1989-)，女，硕士研究生.

基金项目：国家科技重大专项资助项目(2011ZX05056-001-01);海洋公益性行业科研专项资助项目(201205001)

收稿日期：2014-11-24；修回日期:2014-12-06