同塔四回输电线路双端故障测距实用算法

邹 浩，于仲安，吴 彪，邰能灵



同塔四回输电线路双端故障测距实用算法

邹 浩1，于仲安1，吴 彪1，邰能灵2

(1.江西理工大学电气工程与自动化学院，江西 赣州 341000； 2.上海交通大学电子信息与电气工程学院，上海 200240)

基于输电线路的分布式参数模型，提出了一种适用于同塔四回输电线路差动保护装置的故障测距新算法。该算法首先对输电线路参数进行相模变换，选取相互独立的双端同向正序故障分量，依据输电线路双端口理论建立故障测距方程，从而得出精确的故障距离。该算法原理简单，计算量小，避免了一般测距算法需要计算双曲函数、超越方程、牛顿迭代法和搜索法的复杂过程。PSCAD/EMTDC仿真结果表明，该算法测距精度较高，且不受故障距离、过渡电阻、故障类型和两侧电源功角差的影响，有很强的工程实用价值。

继电保护；同塔四回线；分布式参数模型；差动保护装置；故障测距

0 引言

同塔四回输电线路具有输送容量大，占地少，出线走廊窄，投资成本低等一系列优点[1-3]。同塔四回输电线路增加了线间的耦合，且故障类型繁多，增大了输电线路故障分析和计算的难度，对输电线路的继电保护提出了更高的要求，快速准确地测定故障点有利于及时修复线路和保障可靠用电，因此故障测距算法一直是国内外学者研究的热点[4-6]。

目前同塔四回输电线路故障测距算法根据线路测距保护装置所需信息来源分为单端故障测距法和双端故障测距法。双端故障测距法根据利用线路参数的不同分为集中参数模型和分布参数模型，根据两端电气量采样的同步性又分为同步采样和不同步采样。

基于单端电气量的故障测距算法已在电力系统继电保护中得到了广泛的应用[7-8]。文献[7]利用六序分量法对双回线线路进行参数解耦，利用单端电气量构造故障距离函数，通过简单的方程求解就可以得到故障距离。文献[8]提出了一种采用单端工频量进行一回线内及两回线间跨线故障的测距算法。虽然利用线路单端测距算法原理简单，易于实现，但算法只采用线路一端的电气量进行故障定位，在理论上无法避免过渡电阻和分布电容以及系统运行方式的影响。

近年来，由于现代通信技术的发展，使得线路差动保护应用于输电线路故障测距成为可能，输电线路双端故障测距的应用也越来越广泛[4,9]。文献[4]基于双端环流模分量构造同杆四回线故障测距频域观测方程，实现了精确故障定位。文献[9]选取双端环流分量，根据其在故障点电压相等的原理进行故障测距。双端测距算法利用线路两端的电气量基本可以消除过渡电阻对测距的影响，而且保证两端采样数据的同步以消除电源功角差的影响。

文献[4, 7]计算时涉及双曲函数的计算，最后利用迭代法求解故障距离，计算量大。文献[10]通过引入蚁群算法完成对测距函数的优化求解，最后得到故障距离。文献[11-13]虽然避免了迭代法求解，但是需要计算复杂的双曲函数及其反函数，计算复杂。以上算法都为了得到较高故障测距精度而进行了大量的计算。

本文提出的算法利用同塔四回输电线路分布参数模型，选取同向正序故障分量，在基于输电线路双端口型等值电路的基础上，建立故障测距方程。本文算法可运用到同塔四回输电线路差动保护装置中，利用通信通道即可获得对端电流和电压数据，实现同塔四回线路双端故障测距。

1 同塔四回输电线路模型

同塔四回输电线路的结构如图1所示。其中四回线线路从上至下依次为I，II，III，IV。线路采用双侧电源供电，左端和右端电动势分别为m和n，线路全长为。

图1 同塔四回线系统结构

图2为参数对称(即输电线路采用三相循环换位以减少三相参数不平衡)的同塔四回输电线路阻抗模型，图中同塔四回线路I，II，III，IV回线的自阻抗相等均为，每一回线的相间阻抗为，四回线的线间阻抗均为。

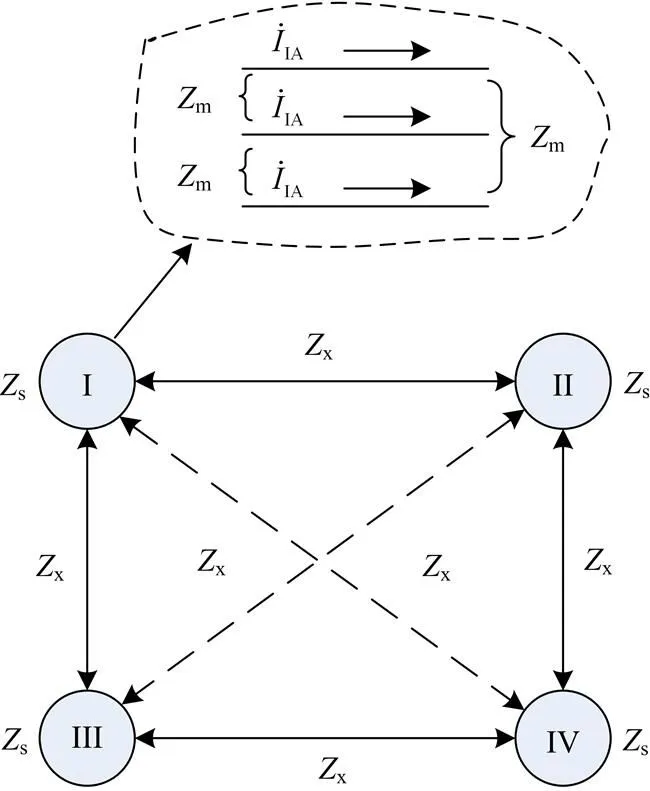
图2 参数对称同塔四回线阻抗模型

2 故障测距算法原理

2.1 分布参数的线路等值模型

对于长线路的同塔四回输电线路，由于充电电流不可忽略，因此需要考虑分布电容，在中长线路中，1/2的集中电容分别连接在线路的两端，形成标准的模型，如图3所示。

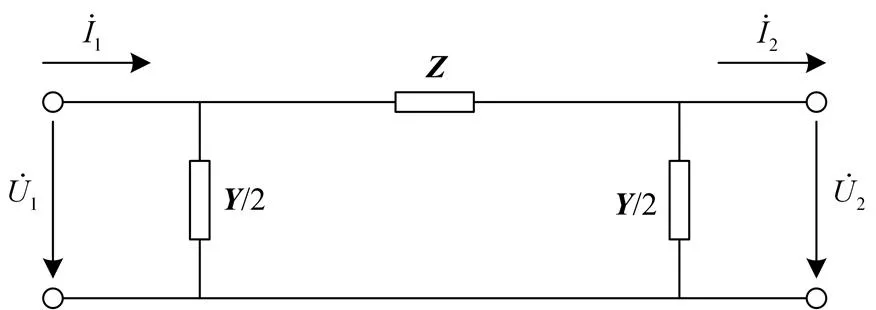
图3 输电线路的双端口型等值电路

当采用图3所示的电流极性规定时，可得到输电线路双端口分布参数型等值电路送端和受端的电压和电流矩阵表达式如式(1)[14]。

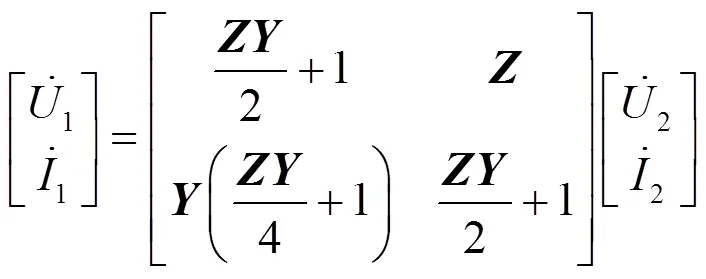
2.2 12序故障序分量分析

在同塔四回输电线路中，电压与电流、系统阻抗之间的关系如式(2)所示。

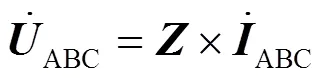
其中

分别为保护安装处I，II，III，IV的电压向量和电流向量。

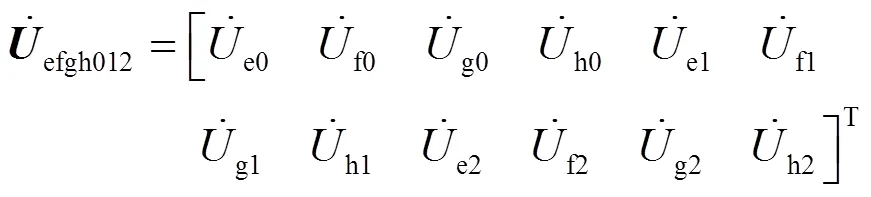
输电线路两端电气量经12序分量变换后得到同向正序分量(e1)、同向负序分量(e2)、同向零序分量(e0)、反向正序分量(f1、g1、h1)、反向负序分量(f2、g2、h2)、反向零序分量(f0、g0、h0)。

12序电压向量和电流向量中只有同向正序e1分量包含同塔四回输电线路各个故障类型的信息，适用于各类故障分析，而且避免了线路零序参数对测距的影响，因此本文选用同向正序分量来进行故障测距计算。

2.3 测距方程建立

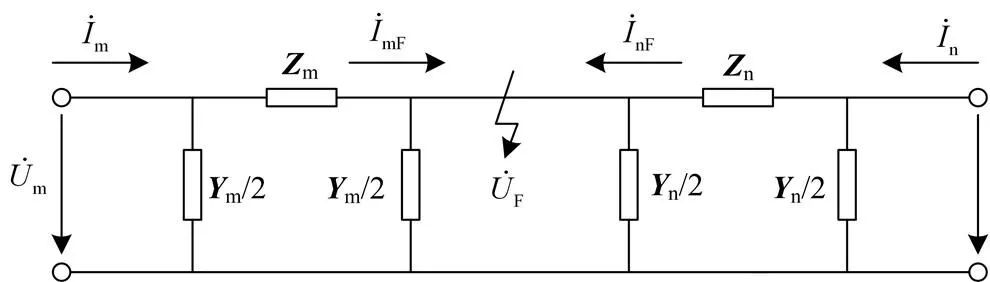
图4 输电线路故障时的双端口型等值电路

由式(1)利用线路两侧电气量可得表达式(3)和(4)。

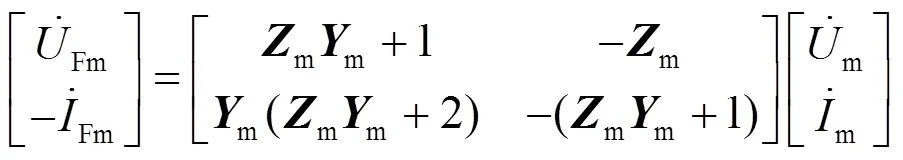
(4)

(6)

通过化简式(6)得到带复数运算的一元二次方程(7)。

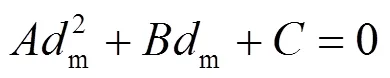
式(7)为复系数方程，实际求解复系数方程时需将其转化为实部方程和虚部方程，只有当这两个方程都有解时，对应的复系数方程才有解。为求解式(7)，令其实部和虚部分别等于0建立一元二次方程为

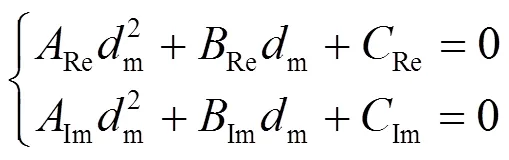
计算上述实系数方程(8)后得到4个解，其中实部和虚部方程分别只有一个满足实际工程测量要求的解。假设满足要求的解分别为、，因此实际求得四回线故障距离为

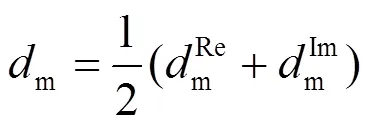
2.4 提高测距精度的办法

考虑到使用双端电气工频量测距，测距精度将受负荷电流的影响，本文为消除负荷电流对测距精度的影响采用系统两端电气工频故障分量进行测距。同塔四回输电线路正常运行时的同向正序电压电流序分量分别为、、、；故障后的同向正序电压电流序分量分别为、、、。由此可得同向正序电压电流故障分量为

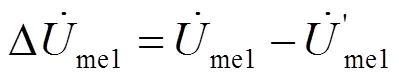
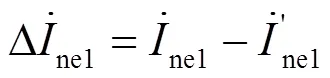
3 仿真验证

为了验证本文新算法的有效性及可行性，利用PSCAD/EMTDC建立相应的仿真模型，仿真模型如图1所示。模型为550 kV双端电源系统，线路全长200 km。m端系统和n端系统正序阻抗为j25 Ω，系统零序阻抗为j40 Ω。线路参数经过解耦后各序网阻抗参数、导纳参数如表1所示。

两侧数据采用故障后150 ms以内的采样数据，基波相量提取采用全波傅式算法。

表2列出了同塔四回输电线路发生各类故障时本文测距方法的测距结果(本文测距方法适用于各类型故障，由于篇幅限制，仅给出典型故障测距结果)，接地过渡电阻和相间过渡电阻假设为10。由表2可知，本文所提测距算法测距精度不受故障位置影响，测距精度较高，最大测距误差不超过0.5%。

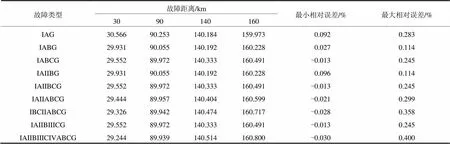
表2 不同位置发生各类故障测距结果

表3列出了同塔四回输电线路故障时过渡电阻对测距精度的影响，假设故障分别为40 km、100 km处不同过渡电阻的IAG故障和IIBIIICG故障。由表3可知，本文算法不受过渡电阻影响，在不同的过渡电阻下，均能达到较高的测距精度，表3中最大误差不超过1%。

为了验证负荷电流对测距精度的影响，表4列出了距离母线m端70 km处，系统两端电源功角差不同时经10W过渡电阻发生单相接地IIBG故障和跨线接地IIBIIICG故障的测距结果。由表4可知，输电线路故障测距结果不受负荷电流的影响，故障测距精度较高。

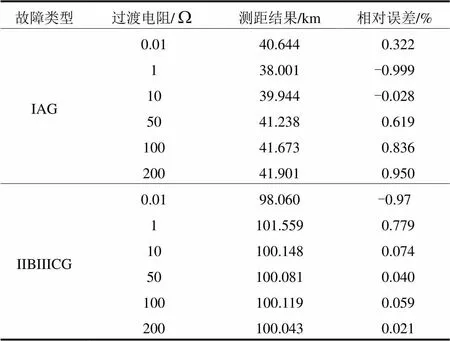
表3 不同故障电阻对测距精度的影响

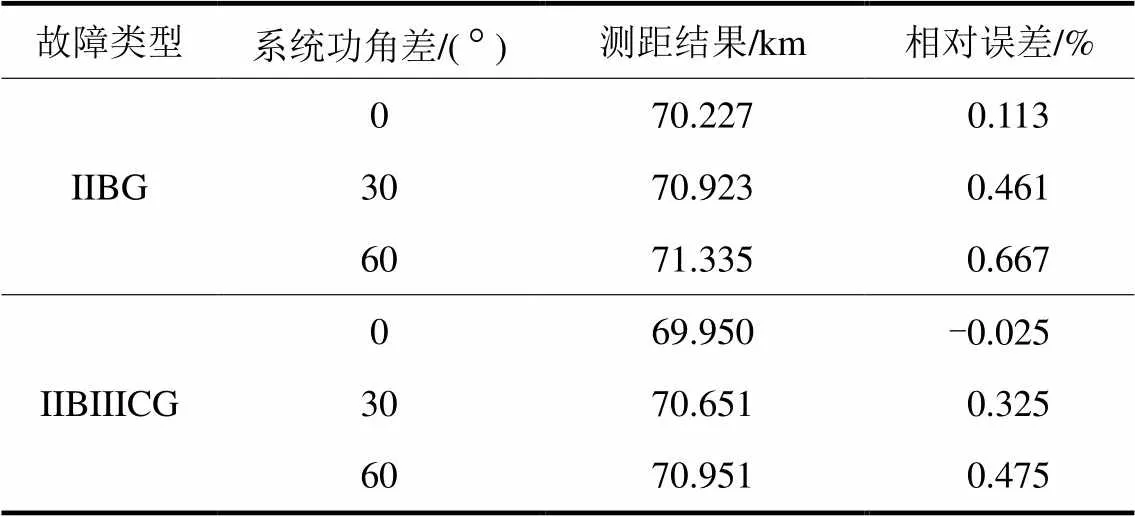
表4 不同电源功角差对测距结果的影响

4 结语

本文针对同塔四回输电线路故障测距问题，提出了一种适用于同塔四回输电线路故障测距的实用新算法。该算法不受四回线线间和相间耦合的影响，采用输电线路分布参数模型，基于双端口网络理论，提取输电线路同向正序故障分量，可消除负荷电流对测距精度的影响，并适用于输电线路各类型故障测距。本算法从工程应用实际出发，原理简单，计算量小，可应用到输电线路差动保护中，利用通道交换得到两侧采样数据，实现双端故障测距。

大量PSCAD/EMTDC实验数据验证结果表明，该算法测距精度较高，且不受故障线路位置、故障类型、过渡电阻及系统两侧电源功角差的影响，具有很强的工程应用价值。

[1] 张颖, 邰能灵. 同塔四回线接地距离保护的分析[J]. 电力系统保护与控制, 2010, 38(12): 1-6.

ZHANG Ying, TAI Nengling. Analysis of ground distance protection for quadruple-circuit transmission lines on the same tower[J].Power System Protection and Control, 2010, 38(12): 1-6.

[2] 张嘉, 葛荣良. 同塔多回输电技术特点及其应用分析[J]. 华东电力, 2005, 33(7): 23-26.

ZHANG Jia, GE Rongliang. Features and application of power transmission technology of multi-circuit lines on the same tower[J]. East China Electric Power, 2005, 33(7): 23-26.

[3] 邰能灵, 郭培育, 于仲安, 等. Π模型电容电流补偿的同塔四回线电流差动保护[J]. 电力系统保护与控制, 2015, 43(12): 34-42.

TAI Nengling, GUO Peiyu, YU Zhongan, et al. Current differential protection using capacitive current compensating algorithm on Pi-model for four-parallel lines on same towers[J]. Power System Protection and Control, 2015, 43(12): 34-42.

[4] 徐鹏, 梁远升, 王钢.同杆四回线参数自适应双端故障测距频域算法[J].电力系统自动化,2010, 34(9): 59-64.

XU Peng, LIANG Yuansheng, WANG Gang. A parameter adaptive fault location with two-terminal data for four- parallel transmission lines on the same tower[J]. Automation of Electric Power Systems, 2010, 34(9): 59-64.

[5] 王海军, 周全, 梁远升, 等. 基于电压突变量的同塔双回直流输电线路故障选线方法[J]. 电力系统保护与控制, 2015, 43(7): 23-29.

WANG Haijun, ZHOU Quan, LIANG Yuansheng, et al. Fault line selection of double-circuit HVDC transmission line based on voltage variation[J]. Power System Protection and Control, 2015, 43(7): 23-29.

[6] 任琴, 舒勤, 刘勇. 基于对称注入法反射波特征提取的配电网故障测距算法[J]. 电力系统保护与控制, 2015, 43(24): 19-25.

REN Qin, SHU Qin, LIU Yong. A fault location algorithm for distribution network based on extracting features from the reflected wave of symmetrical injection method[J]. Power System Protection and Control, 2015, 43(24): 19-25.

[7] 范春菊, 蔡华嵘, 郁惟镛. 基于六序分量法的同杆双回线精确故障测距[J]. 上海交通大学学报, 2004, 38(8): 1279-1282.

FAN Chunju, CAI Huarong, YU Weiyong. Accurate fault location for parallel transmission line based on six-sequence fault components[J]. Journal of Shanghai Jiao Tong University, 2004, 38(8): 1279-1282.

[8] 李博通, 李永丽, 张朝乾. 基于双回反向序网的同杆四回线单端故障测距算法[J]. 天津大学学报, 2014, 47(5): 433-440.

LI Botong, LI Yongli, ZHANG Zhaoqian. A new fault location algorithm with one end-data for four-circuit transmission line based on double differential network[J]. Journal of Tianjin University, 2014, 38(8): 433-440.

[9] 龚震东, 范春菊, 田羽. 一种适合于同杆4回线的故障测距方法[J].电力系统自动化, 2007, 31(23): 70-73.

GONG Zhendong, FAN Chunju, TIAN Yu. A fault location algorithm suitable for jointed four transmission lines[J]. Automation of Electric Power Systems, 2007, 31(23): 70-73.

[10] 刘迅, 黄纯. 蚁群算法在超高压输电线路故障测距的应用[J]. 电力系统及其自动化学报, 2012, 24(5): 132-137.

LIU Xun, HUANG Chun. Fault location for EHV transmission line based on ant colony algorithm[J]. Proceedings of the CSU-EPSA, 2012, 24(5): 132-137.

[11] 吴瑞春, 焦彦军, 张新国. 双端测距以及同步算法的实现[J]. 继电器, 2008, 36(5): 7-9.

WU Ruichun, JIAO Yanjun, ZHANG Xinguo. Realization of two-terminal fault location and synchronization algorithm[J]. Relay, 2008, 36(5): 7-9.

[12] 张晓明, 徐岩, 王瑜, 等.一种基于参数检测的双端故障测距算法[J].电力系统保护与控制, 2011, 39(12): 106-111.

ZHANG Xiaoming, XU Yan, WANG Yu, et al. A fault location algorithm for two-terminal transmission lines based on parameter detection[J]. Power System Protection and Control, 2011, 39(12): 106-111.

[13] 林富洪, 王增平, 李金龙, 等. 基于双曲正弦函数相位特性高压故障线路相位测距法[J]. 电力系统保护与控制, 2010, 38(14): 28-33, 97.

LIN Fuhong, WANG Zengping, LI Jinlong, et al. Fault location algorithm for HV transmission line based on phase characteristics of hyperbolic sine function[J]. Power System Protection and Control, 2010, 38(14): 28-33, 97.

[14] 刘振亚.特高压电网[M].北京: 中国经济出版社,2005.

[15] 田羽, 范春菊, 龚振东.同杆4回线12序分量法[J].电力系统自动化, 2007, 31(21): 35-39.

TIAN Yu, FAN Chunju, GONG Zhendong. A study on twelve-sequence component method of four-parallel lines on the same towers[J]. Automation of Electric Power Systems, 2007, 31(21): 35-39.

(编辑 魏小丽)

A new method of fault location with two-terminal data for four-parallel transmission lines on the same tower

ZOU Hao1, YU Zhongan1, WU Biao1, TAI Nengling2

(1. School of Electrical Engineering and Automation, Jiangxi University of Science and Technology, Ganzhou 341000, China; 2. School of Electronic, Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Based on distributed parameter model of transmission lines, this paper proposes a new fault locating practical algorithm suitable for the four-circuit transmission line on the same tower differential protection device. Firstly, the transmission line parameters are carried out phase-mode transformation, independent double-ended with the positive sequence fault components are selected, and according to the theory of establishing a dual-port transmission line fault location equation, the accurate fault location is obtained. The method is simple and has less calculation amount, which avoids the complex process of a general ranging method, such as calculating the hyperbolic functions, transcendental equations, Newton iterative method and search methods. PSCAD/EMTDC simulation results show that the algorithm has high fault accuracy, and is immune to fault distance, transition resistance, fault type and power angle difference of double sides power sources, so it has practical value of engineering. This work is supported by National Natural Science Foundation of China (No. 51177066).

protective relaying; four-parallel lines on the same tower; distributed parameter model; differential protection device; fault location

10.7667/PSPC151954

国家自然科学基金资助项目(51177066)

2015-11-07；

2016-01-02

邹 浩(1991-)，男，硕士研究生，主要研究方向为电力系统继电保护与控制；于仲安(1973-)，男，硕士，副教授，硕士生导师，主要从事电力系统分析、计算机监控技术及应用的研究工作；吴 彪(1990-)，男，硕士研究生，主要研究方向为电力系统继电保护与控制。E-mail: 1249428143@qq.com