多因素扰动情景下应急数量弹性契约的供应链协调
2016-04-11史文强冯良清
刘 浪,史文强,冯良清
(1.华东交通大学经济管理学院,江西 南昌 330013; 2.航空经济发展河南省协同创新中心,河南 郑州 450046;3.南昌航空大学经济管理学院,江西 南昌 330063)
多因素扰动情景下应急数量弹性契约的供应链协调
刘 浪1,2,史文强3,冯良清3
(1.华东交通大学经济管理学院,江西 南昌 330013; 2.航空经济发展河南省协同创新中心,河南 郑州 450046;3.南昌航空大学经济管理学院,江西 南昌 330063)
研究突发事件发生导致多种因素干扰的情景下,数量弹性契约是否能实现二级供应链协调,并寻找供应链协调时最优订货与定价策略。针对市场价格稳定和随机两种情况,设定契约弹性系数为常量,分别建立市场价格稳定不变与随机波动两种情况下的应急数量弹性契约模型,寻找它们实现协调的内在约束条件,并与基准模型下的结论进行比较。然后将契约弹性系数由常量拓展为变量,判断是否同时存在最优的弹性系数和订货量,分析弹性系数的变化对于生产、订货决策及供应链整体收益的影响。研究结果证明:当弹性系数为常量时,只要对基准契约的批发价进行适当调整,供应链就能协调应对两种情景下的突发事件,此时,可以找到唯一的最优订货决策。当弹性系数为变量时,两种情景下的供应链均不存在唯一的最优订货决策,但存在唯一的最优供货决策,并且契约弹性系数的改变不会影响供应链期望收益。最后通过算例验证了上述结论的正确性。
稳定价格;随机价格;应急数量弹性契约;供应链协调
1 引言
近年来,突发事件频频发生,如2003年的SARS事件,2005年的“苏丹红”事件,2008 年初我国南方雨雪冰冻灾害,2008 年 5 月 12 日的“汶川大地震”,2010 年8月7 日甘肃舟曲特大泥石流,2011年日本核泄漏,2013年的禽流感事件,突发事件的暴发会给原本协调的供应链带来冲击,破坏供应链的平衡。突发事件破坏力的大小直接影响供应链契约中相关参数的变化,若暴发普通的突发事件,只会造成市场需求小幅波动;若暴发破坏力特别大的突发事件,则会造成社会恐慌以及其他连锁反应,引起市场需求波动加大,引得市场价格大幅涨跌,致使供应链从协调转为失调。当突发事件造成市场价格随机波动后,如何使供应链从失调重新恢复到协调,已成为应急供应链管理研究的热点问题之一。本文主要研究突发事件引起市场价格随机变化后,数量弹性契约下供应链是否还能实现协调,并将其与价格稳定不变的情况进行对比,探讨它们应对突发事件规律的异同。
数量弹性(柔性)契约(Quantity Flexibility Contract)指生产商按照高于最初订购的产量组织生产,且允许零售商在市场需求变化后可以改变最初订货量,并规定了最大的订货波动比例(弹性系数)的协议。当前,理论界对于此类问题的研究正在逐步深入。早期学者从订货周期的角度来构建契约,如Lariviere[1]最早建立了外界环境确定的单周期数量弹性契约模型。后来Tsay[2]建立了多周期数量弹性契约模型。Tsay和Lovejoy[3],Sethi等[4]分析了数量弹性契约模型中多级、多周期的运营模式对供应链的影响。之后,学者们广泛研究供应链上成员数量不同的单周期二级供应链,如Karakaya和Bakal[5]研究了供应商提供异质产品时,单供应商、单零售商组成的二级供应链的数量弹性契约模型。Kim等[6]则研究了多供应商和单零售商组成的二级供应链的数量弹性契约。也有学者从其他角度研究数量弹性契约下的供应链运作模式,如Lian Zhaotong和Deshmukh[7]研究了FOP和FOPII两种启发式方法,并制定了供应商及零售商的生产订货决策。Chan等[8]建立了分布式约束的数量弹性契约,并证明该机制能够消除不确定性因素的影响。Subramanian等[9]运用模拟和优化技术,研究了需求不平稳的数量弹性契约对供应链的影响。朱海波和胡文[10]通过有限情境表述客户需求不确定性,并运用期权、数量柔性契约的混合契约研究了多周期两级供应链的协调问题,给出了供应链中各决策主体的最优决策。后来有许多学者研究数量弹性契约与其他契约融合,如Chung等[11]将价格折扣激励契约与数量弹性契约混合,Lumsakul和 Luong[12]将收益共享契约与数量弹性契约混合,胡本勇等[13-15]比较了单向看涨期权及双向期权两种期权类型下的数量弹性模型,并进一步分析资金约束对期权与数量弹性混合契约的影响。杨建华等[16]则运用回购契约构建了买方市场时效性产品的数量弹性契约模型,研究表明优化的模型能够促使分销商按实际预测量订货。覃艳华[17]构建了零售商的需求及退货量受其努力程度和退货价格影响的数量弹性契约模型,证明引入回馈与惩罚契约策略的数量弹性契约就能够实现供应链协调。刘臣等[18]建立了数量弹性契约下选择供应商数量的整数规划模型,对比分析了不同数量的供应商面临的风险程度。刘咏梅等[19]研究了数量弹性契约条件下,零售商风险规避的问题,指出在一定条件下调整弹性系数及批发价都可以使供应链协调。上述文献大多都是针对稳定的外界环境,运用数量弹性契约来协调供应链,寻找最优的订货与定价策略。少数学者研究了外界环境不确定即发生突发事件的情况,但研究的对象仅仅是造成需求波动的突发事件,并没研究造成供应链契约中其他参数发生变化的突发事件。本文将主要讨论在突发事件引起市场需求大幅波动,市场价格并随市场需求随机变化的情形下,寻找运用数量弹性契约再次实现二级供应链协调的内在约束条件。同时将其与不会使价格波动的突发事件情景下进行对比,并考察契约弹性系统变化对供应链协调的影响。
2 基准二级供应链的数量弹性契约模型
以最简单的二级供应链为研究对象,考虑供应链上下游企业按照数量弹性契约组织生产订货,并计算供应链上各级节点企业的最优期望收益及订货量,通过调整商品批发价来实现供应链协调。
假设1:供应链上的商品均为易逝品及短周期产品,产品的市场需求随机,市场价格稳定;零售商为了满足商品的持续供给,需要根据历史数据及对市场的观察,提前预测市场需求量。
假设2:供、售双方最终商品单位残值相等。
假设3:供应链上成员之间信息对称,即供应商和零售商相互之间不隐瞒成本等相关信息,并针对市场需求共同协商制定契约条款。
假设4:供应商及零售商的风险偏好为风险中性。
设单位产品市场价格为p0,在基准模型中是一个常量。上游企业以批发价格w给下游企业提供产品;gs和gr分别为供应商和零售商的缺货单位商誉惩罚成本,供应链缺货单位商誉惩罚成本记作g=gr+gs;零售商的单位边际成本为cr,供应商单位边际生产成本为cs,整体供应链的单位边际成本记作c=cr+cs;在季节末未销售出去的商品单位边际残值为v。

供应链以下面方式运行:首先由供应链上下游企业联合对市场随机需求x进行预测,并获得其分布函数,然后双方协商, 确定订货量可上下波动比例(即弹性系数)的范围,下游企业开始根据预测提出初始商品订货量q,并告知上游企业;上游企业根据下游企业提供的订货量q依照契约组织生产,实际生产数量为Q=(1+α)q,且最多提供这么多的商品。进入实际销售阶段,零售商在[(1-β)q,(1+α)q]之间的范围内从供应商处灵活购买。



根据上述各种假设及数量弹性契约的运作过程,可得零售商的期望收益函数为:
(1)
供应商的期望收益函数为:
(2)
整体供应链的期望收益函数为:
(3)
根据供应链协调的判断依据:在各节点企业最优订货量与整体供应链最优订货量相等的同时,零售商(或供应商)期望收益与整体供应链期望收益成仿射关系(见刘臣等[18])。
据此,对公式(3)分别求q的一阶、二阶导数,可得:
(4)
(5)

令(4)式等于零,可得最优订货量q*为(6)式的解:
(p0-v+g-cr)(1+α)(1-F(q(1+α)))-cr(1-β)F(q(1-β))-(cS-v)(1+α)=0
(6)
命题1如果没有发生突发事件,需求函数维持不变,当:

(7)
其中:参数满足1>η>0,η,为供应链的利润分配系数,由零售商与供应商的谈判能力决定,在数量弹性契约下能实现供应链协调。
证明:将(7)式代入式(1)可以得到:
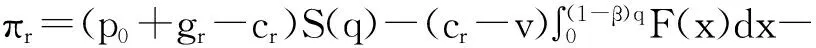
(8)
这时零售商与整体供应链的期望收益函数成仿射关系,即零售商的期望收益可以用供应链的期望收益来线性表示,零售商与供应链系统二者具有相同的最优订货量q*。说明此时在数量弹性契约下可以实现二级供应链协调。
上面研究的是无突事件下的情形,下面将研究在突发事件下的两种情形,第一种是普通的突发事件仅造成市场需求小幅扰动,但市场价格稳定不变的;第二种是破坏性大的突发事件造成市场需求大幅震荡且市场价格随机波动,分析这两种情形下的供应链上相关参数变化对最优决策的影响。
3 价格稳定条件下应急数量弹性契约的供应链协调
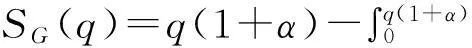
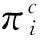
零售商的期望收益函数为:
(9)
供应商的期望收益函数为:
(10)
供应链的期望收益函数为:
(11)
命题2 价格稳定的突发事件发生后,需求规模出现波动,若仍采用基准数量弹性契约的调整值,数量弹性契约不能实现供应链协调。
证明:将(7)式代入(9)式,可以得到:
又根据供应链的收益(11)式,上式可简化为:
λ2(Q*-NG(q))+]
由此可知,当不引起市场价格波动的突发事件暴发后,供应链最优订货量比基准契约情况下的要大,零售商与整体供应链的期望收益函数不成仿射关系,若继续采用基准数量弹性契约下的订货量,供应链失调。
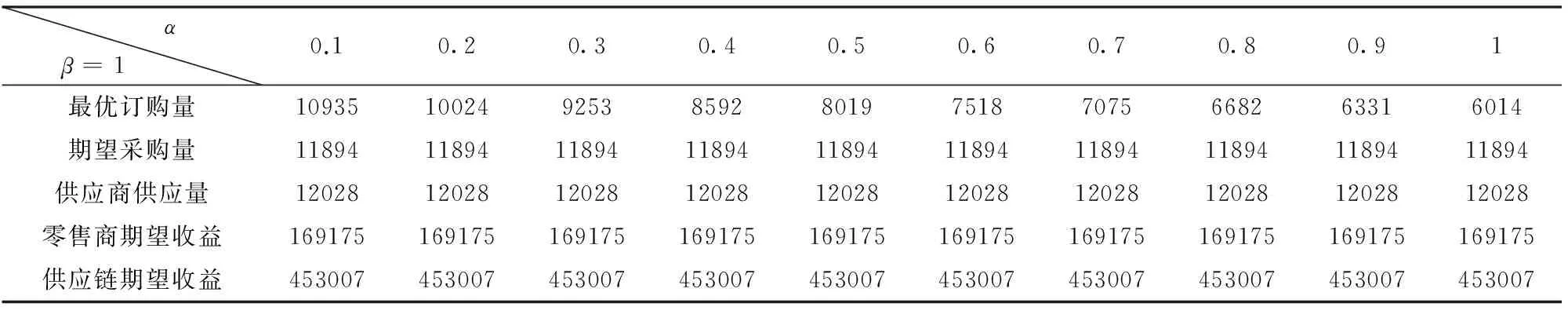
命题3 当不影响市场价格稳定的突发事件发生后,市场规模发生变化,在期望订货量分别超过或低于基准模型的最优生产量时,即NG(q)>Q*或者NG(q) (12) 此时数量弹性契约能够实现供应链协调。 依照供应链系统的收益函数,上式可变形为: (13) 3.1 价格稳定下契约参数α,β为常量时最优订货决策 本节假设契约上下行弹性系数α,β皆为常量,它们的大小由供应链上节点企业谈判能力决定。令p0-v+g-cr-λ1>0,且突发事件造成市场需求增大,但市场价格不发生变化。即当NG(q)>Q*时,由(11)式可得此时供应链期望收益的表达式: (14) 对式(14)求q的一阶及二阶导数,得: (15) (16) (p0-v+g-cr-λ1)(1+α)(1-G(q(1+α)))-(cr+λ1)(1-β)G(q(1-β))-(cs-v)(1+α)=0 (17) 同理可得,满足p0-v+g-cr-λ2>0时,当NG(q) (18) (p0-v+g-cr+λ2)(1+α)(1-G(q(1+α)))-(cr-λ2)(1-β)G(q(1-β))-(cs-v)(1+α)=0 (19) 3.2 价格稳定下契约参数α,β为变量时最优订货决策 当市场需求增大时,对供应链收益表达式(14)分别求q,α,β的一阶及二阶导数。 前文已经对(14)式求了q的一阶和二阶导数,得(15)式和(16)式,从(15)、(16)式可知收益函数是一个凹函数,存在唯一的最优订货量,能使收益达到最大值。最优的订货量可以通过(17)式求得。 其次,对(14)式求α的一阶和二阶导数得: (20) (21) 若存在最优的上行弹性系数α*,(20)式必为零,则存在唯一的α*,其解可通过(22)式求得: [(p0-v+g-cr-λ1)(1-G(Q))-cs+v]q=0 (22) 再次对(14)式求β的一阶及二段导数得: (23) (24) 若供应链系统中存在最优的下行弹性系统β*,则式(23)必等于零,并且式(24)小于零。但是,由于cr+λ1>0,若式(23)等于零,则必有β=1。此时式(24)结果也将为零。因此,无法判断β是否存在最优解。若存在最优解,则必有β=1。此时,将β=1代入(15)和(16)式,可化简为: (25) (26) 令公式(25)等于零,可得: [(p0-v+g-cr-λ1)(1-G(Q))-cs+v](1+α)=0 (27) 因为(1+α)与q都不等于零,因此(22)与(27)式简化为一个共式: (p0-v+g-cr-λ1)(1-G(Q))-cs+v=0 (28) [(p0-v+g-cr+λ2)(1-G(Q))-cs+v]q=0 (29) [(p0-v+g-cr+λ2)(1-G(Q))-cs+v]cs+v](1+α)=0 (30) (29)与(30)式也可简化为一个共式: (p0-v+g-cr+λ2)(1-G(Q))-cs+v=0 (31) 据此,可得到价格随机的突发事件发生后零售商的期望收益函数为: (32) 为了简化表达,令: 供应商的期望收益函数为: (33) 为了简化表达,同时设: B=λ1(NH(q)-Q*)++λ2(Q*-NH(q))+]。 供应链的期望收益函数为: (34) 命题4 当暴发破坏力大的突发事件发生后,引起市场需求大幅度变动,市场价格也随机波动,如果依旧采用基准数量弹性契约,则不能实现供应链协调。 证明:将基准契约下的批发价(7)式代入价格随机条件下零售商期望收益函数(32)式,可得到: (35) 此时零售商的收益函数不再是供应链系统收益的仿射函数。 由此可见,当暴发破坏力大的突发事件发生后,引起市场需求大幅度变动(NH(q)>Q*或NH(q) 命题5当破坏力大的突发事件暴发后,市场需求大幅变动,市场价格也随机波动,在订货量分别超过或低于基准模型的订货量时,即NH(q)>Q*或NH(q) (36) 调整后的数量弹性契约下能够实现二级供应链协调。 证明:将(36)式代入(32)式,可以得到: 用供应链的收益函数将零售商的期望收益表达出来,即将(34)式代入上式,可得: (37) 4.1 随机价格下契约参数α,β为常量时最优订货决策 本节假设契约上下行弹性系数α,β为固定常数,不随供应链的市场规模大小进行相应的调整,仍由供应链上下节点企业谈判能力决定。令p0+α(μH-Q)+g-v-cr-λ1>0,当市场需求扩大,即NH(q)>Q*时,整体供应链的期望收益函数可表示为: (38) 对(38)式求q的一阶及二阶导数: (39) (40) -(1+α)[(αSH(q)-v+cs)-(cr+λ1)(1-β)H(q(1-β))-(p0+α(μH-Q)+g-v-cr-λ1)(1-H(Q))]=0 (41) -(1+α)[(αSH(q)-v+cs)-(cr+λ2)(1-β)H(q(1-β))-(p0+α(μH-Q)+g-v-cr+λ2)(1-H(Q))]=0 (42) 4.2 随机价格下契约参数α,β为变量时最优订货决策 当NH(q)>Q*时,收益表达式为(38)式,对(38)式分别求q,α,β的一阶及二阶导数。 其次,对(38)式求α的一阶和二阶导数得: (43) (44) 若存在最优的上行弹性系数α*,(43)式必为零,则存在唯一的α*,且为(45)式的解: -q[(αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr+λ1)(1-H(Q))]=0 (45) 再次求β的一阶及二阶导数: (46) (47) 若供应链系统中存在最优的下行弹性系统β*,则式(46)必等于零,并且式(47)小于零。但是,由于cr+λ1>0,若式(46)等于零,则必有β=1。此时式(47)也等于零。因此,无法判断β是否存在最优解。若存在最优解,则必有β=1。此时,不妨将β=1代入(39)和(40)式,可化简为: (48) (49) -(1+α)[(αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr-λ1)(1-H(Q))]=0 (50) -q[(αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr-λ1)(1-H(Q))]=0 (51) 因为(1+α)不等于零,q也不等于零,因此(50)与(51)式可简化为一个共式: (αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr-λ1)(1-H(Q))=0 (52) -(1+α)[(αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr-λ1)(1-H(Q))]=0 (53) -q[(αSH(q)-v+cs)+(p0+α(μH-Q)+g-v-cr+λ2)(1-H(Q))=0 (54) (41)与(42)式也可简化为一个共式: (αSH(q)-v+cs)-(p0+α(μH-Q)+g-v-cr+λ2)(1-H(Q))]=0 (55) 假设某种应急药品,在正常情况下每箱药品的销售价格p0=120元,供应商的生产成本cs=50元,零售商边际单位成本cr=30元,供、售双方的缺货单位商誉损失成本分别为gs=2元与gr=3元,单位产品残值ν=20元,设η=0.4。当发生突发事件后,额外增加的单位生产成本λ1=10元,处理费用λ2=20元,市场规模系数α=0.004。实际销售时,可能有以下几种情形: (1)在正常的情况下,市场需求服从 X~ N(10000,3002) 的正态分布; (2)当突发事件不影响市场价格,但造成市场需求扩大(NG(q)>Q*),市场需求X~N(12000,3002)的正态分布; (3)当突发事件不影响市场价格,但造成市场需求缩小(NG(q)>Q*),市场需求X~N(8000,3002) 的正态分布; (4)当突发事件造成市场价格随机波动,且造成市场需求扩大(NG(q)>Q*),市场需求服从 X~ N(20000,3002) 的正态分布; (5)当突发事件造成市场价格随机波动,且造成市场需求缩小(NG(q)>Q*)时,市场需求服从 X~ N(6000,3002)的正态分布。 5.1 弹性系数α,β为常量时供应链协调算例分析 假设事先约定契约的弹性系数为常量,令α=0.3,β=0.2。下面以Worfram Mathematic为工具,分别针对无突发事件在基准契约下,引起价格稳定与价格随机的突发事件分别在基准契约与调整后的契约下,考虑市场规模扩大与缩小两种情形,分别计算各种情况下的最优订货量、批发价,以及供、销双方和整体供应链的期望收益。并分析不同情景下供应链协调的情况,相关数据计算结果见表1。 表1 9种情况下的数据对比表 案例数据分析: (1)在同种状态下,批发价的调整不会造成最优订货量的改变,并且不会造成供应链整体收益的变化,批发价的改变仅会影响供应链整体收益在各节点企业之间的分配。 (3)当引起价格稳定的突发事件造成市场需求增大时,若仍采用基准契约,零售商期望收益的增幅将大于供应商期望收益的增幅,分别为19.97%、13.25%,而供应链期望收益增长15.77%;当引起随机价格的突发事件造成市场需求增大后,若仍延用基准契约,各节点期望收益均会增长,但增长极不均衡。零售商期望收益将增长254.41%,供应商期望收益仅增长25.78%,供应链期望收益增长111.42%。可见在市场需求增加时,依旧采取基准契约,不管理价格稳定还是价格随机的背景下,供应链上成员期望收益的增幅与整体供应链的不一致,尤其是引起价格随机的突发事件更是使得零售商的收益波动巨大,供应链无法达到协调。 (4)当引起价格稳定的突发事件造成市场需求减小时,仍然采取基准契约协调,零售商、供应商和供应链的期望收益都将出现小幅减少,减幅分别为19.91% 、38.30%、和31.41%;当引起随机价格的突发事件造成市场需求减少时,供应链上各节点企业期望收益减幅较大,其中零售商减少40.37%,供应商则减少75.53%,供应链整体收益减少62.36%。市场规模减小时,不管是价格稳定还是价格随机的背景下,供应链上成员期望收益与整体供应链期望收益的减幅不一致,此时供应链无法协调。 (5)当引起价格稳定的突发事件发生使市场需求增加时,若采用调整后的契约,零售商、供应商和供应链的期望收益分别增长15.42%,15.97%,15.46%;当引起随机价格的突发事件使市场需求增加时,采用调整后的契约,零售商、供应商和供应链的期望收益分别上涨112.12%,110.01%,111.42%。可见,不管是价格稳定还是价格随机的背景下,突发事件造成市场需求增加时,采用调整后的契约,各节点期望收益增幅保持一致,供应链能够实现协调。 (6)当引起价格稳定的突发事件使得市场需求规模缩小时,采取调整后的契约,零售商、供应商和供应链的期望收益分别减少32.20%,30.94%,31.41%;当引起随机价格的突发事件造成的市场需求减少时,采取调整后的契约,零售商、供应商和供应链的期望收益分别减少63.90%,61.44%,62.36%。可见,不管是价格稳定还是价格随机的背景下,供应链上成员期望收益的减幅与整体供应链的减幅基本一致,此时供应链协调。 5.2 弹性系数α,β为变量时对供应链相关要素的影响 下面分别在引起市场价格稳定和随机的突发事件背景下,考虑造成市场需求扩大或缩小两种情形,研究弹性系数变化对零售商订购量、零售商期望采购量、供销商供货量、零售商期望利润与供应链期望利润的影响。为了不失一般性,本文只研究在β=1,α在[0.1,1]区间变化、β=0.2,α在[0.1,1]区间变化和α=0.3,β在[0.1,1]区间变化三种情况。利用Worfram Mathematic为工具,通过计算,可列出上述12种计算结果见附表2-13。 表2 价格稳定背景下,市场需求扩大,β=1和α在[0.1,1]区间变化的仿真结果 表3 价格稳定背景下,市场需求扩大,β=0.2和α在[0.1,1]区间变化的仿真结果 表4 价格稳定背景下,市场需求扩大,α=0.3和β在[0.1,1]区间变化的仿真结果 表5 价格稳定背景下,市场需求缩小,β=1和α在[0.1,1]区间变化的仿真结果 表6 价格稳定背景下,市场需求缩小,β=0.2和α在[0.1,1]区间变化的仿真结果 表7 价格稳定背景下,市场需求缩小,α=0.3和β在[0.1,1]区间变化的仿真结果 表8 价格随机背景下,市场需求扩大,β=1和α在[0.1,1]区间变化的仿真结果 表9 价格随机背景下,市场需求扩大,β=0.2和α在[0.1,1]区间变化的仿真结果 表10 价格随机背景下,市场需求扩大,α=0.3和β在[0.1,1]区间变化的仿真结果 表11 价格随机背景下,市场需求缩小,β=1和α在[0.1,1]区间变化的仿真结果 表12 价格随机背景下,市场需求缩小,β=1和α在[0.1,1]区间变化的仿真结果 表13 价格随机定背景下,市场需求缩小时,α=0.3和β在[0.1,1]区间变化的仿真结果 案例分析: (1)从表4、表7、表10和表13可以看出,如果上行弹性系数α为常量,每种突发事件状态下,存在唯一的最优订货和供货决策。从其他的8个表中可以看,如果上行弹性系数α为变量,每种突发事件状态下,不存在唯一的最优订货决策,但存在唯一的供货决策。 (2)从表2和表3可以看出,市场价格稳定时,当市场需求增大时,上行弹性系数α变化,对零售商的期望采购量(N(q)*)、供应商的最优供应量(Q*)、零售商的期望收益πr和供应链的期望收益πh均无影响,只会影响零售商的最优订购量(q*)。下行弹性系数β变化,对上述5个要素均没有影响。且知,供应商最优供应量大于零售商的期望采购量(即Q*>N(q)*)。 (3)从表5和表6可以看出,市场价格稳定时,当市场需求势缩小时,与市场需求增大时得出的结论完全一样。 (4)从表4和表7可以看出,市场价格稳定时,不管是市场需求增大还是缩小,下行弹性系数β的变化,对期望采购量、最优供应量、零售商期望收益和供应链期望收益没有影响 (5)从表8和表9可以看出,当市场价格随机、市场需求增大时,上行弹性系数α的变化,对零售商的期望采购量(N(q)*)、供应商的最优供应量(Q*)、零售商的期望收益πr和供应链的期望收益πh均无影响,只会影响零售商的最优订购量(q*)。从表10可以看出,下行弹性系数β的变化,对上述5个要素均没有影响。但供应商的最优供应量等于零售商的期望采购量(即Q*=N(q)*)。 (6)从表11、表12和表13可以看出,当市场价格随机、市场需求势缩小时,与当市场价格稳定,市场需求缩小时的结论完全一样。除了表10,其他11个表格中,供应商的最优供应量均大于零售商的期望采购量(即Q*>N(q)*)。 通过对上述问题的研究,可以得出以下结论: (1)不管突发事件造成市场价格稳定不变还是随机变化,基准数量弹性契约下,二级供应链均不能实现协调,若分别对批发价做出适当的调整,二级供应链均能恢复协调。 (2)不管市场价格稳定不变还是随机变化,不管是市场需求增大还是缩小,上行弹性系数α变化,在聚中决策下,对零售商的期望采购量(N(q)*)、供应商的最优供应量(Q*)、零售商的期望收益πr和供应链的期望收益πh均无影响,只会影响零售商的最优订购量(Q*)。下行弹性系数β变化,对上述5个要素均没有影响。但只有在市场价格随机变化、市场需求增大的情况下,供应商的最优供应量等于零售商的期望采购量(即Q*=N(q)*);其他情况下的供应商最优供应量均大于零售商的期望订购量(即Q*>N(q)*),说明在这些情况下的供应商会出现剩余库存。对上述所有情况而言,供应商的剩余库存会大于或等于零,也就是说供应商是不会出现缺货的现象。这对缺货损失有风险规避的供应商而言,在现实生活中,采用数量弹性契约是上上之策。 (3)无论是从理论证明,还是从算例仿真来看,下行弹性系数β对整体供应链的绩效、供应链上成员的绩效、零售商的期望采购量N(q)*、供应商的最优供应量Q*均无影响,它只会影响批发价的调整。因为批发价只是个中间变量,这也说明下行弹性系数β也是个中间变量。它只有在分散决策时影响供应链整体收益在供应链上成员之间分配,在集中决策时对整体供应链及供应链上成员的绩效没有影响。 (4)从结论(2)和(3)还可归纳出,如果上行弹性系数α为常量,每种突发事件状态下,存在唯一的最优订货与供货决策;如果上行弹性系数α为变量,则不存在唯一的最优订货决策,但存在唯一的最优供货决策。下行弹性系数β对订货与供货决策没有影响。 本文研究的前提假设是信息对称、供应链参与者为风险中性。进一步可研究信息不对称,供应链参与者有风险规避的应急数量弹性契约下的供应链协调。 [1] Lariviere M A. Supply chain contracting and coordination with stochastic demand, quantitative models for supply chain management [M].Boston:Kluwer Academic Publishers, 1999. [2] Tsay A A. The quantity flexibility contract and supplier-customer incentives [J]. Management Science, 1999, 45(10): 1339-1358. [3] Tsay A A, Lovejoy W S.Quantity flexibility contracts and supply chain performance [J]. Manufacturing and Service Operations Management, 1999, 1(2):89-111. [4] Sethi S P, Yan Houmin, Zhang Hanqin. Quantity flexibility contracts: Optimal decisions with information updates [J]. Decision Sciences, 2004, 35(4): 691-712. [5] Karakaya S, BakalS S. Joint quantity flexibility for multiple products in a decentralized supply chain [J]. Computers & Industrial Engineering, 2013, 64(2): 696-707. [6] Kim J S, Park S I, Shin K Y. A quantity flexibility contract model for a system with heterogeneous suppliers [J]. Computers & Operations Research, 2014, 41: 98-108. [7] Lian Zhaotong, Deshmukh A. Analysis of supply contracts with quantity flexibility [J]. European Journal of Operational Research, 2009, 196(2): 526-533. [8] Chan F T S, Chan H K. A simulation study with quantity flexibility in a supply chain subjected to uncertainties [J]. International Journal of Computer Integrated Manufacturing, 2006, 19(2): 148-160. [9] Subramanian V, Pekny J F, Reklaitis G V. Decentralized supply chain dynamics and the quantity flexibility contract [J]. Computer Aided Chemical Engineering, 2006, 21: 2153-2158. [10] 朱海波,胡文. 基于期权的供应链数量柔性契约决策模型[J]. 控制与决策,2014,29(5):860-866. [11] Chung W M, Talluri S, Narasimhan R. Quantity flexibility contract in the presence of discount incentive [J]. Decision Sciences, 2014, 45(1): 49-79. [12] Lumsakul P, Luong H T. Development of a composite revenue sharing-quantity flexibility contract [J]. Industrial Engineeering & Management Systems, 2013, 12(3): 224-233. [13] 胡本勇,王性玉,彭其渊. 供应链单向及双向期权柔性契约比较分析[J]. 中国管理科学,2007,15(6):92-97. [14] 胡本勇,王性玉,彭其渊. 供应链柔性契约与单向及双向期权模式选择[J]. 系统管理学报,2009,18(2):165-171. [15] 胡本勇,彭其渊,王性玉. 考虑采购资金约束的供应链期权柔性契约[J]. 管理科学学报,2009,12(6):62-71. [16] 杨建华,牛坤,于本海,等. 买方市场时效性产品的供应链弹性契约优化模型[J]. 中国管理科学,2013,29(5):80-85. [17] 覃艳华. 考虑努力及退货价格因素的易逝品供应链弹性数量契约模型[J]. 华中师范大学学报(自然科学版),2012,46(4): 477-482,487. [18] 刘臣,张庆普,单伟. 基于数量弹性契约的供应商数量选择问题研究[J]. 运筹与管理,2010,19(4):1-7. [19] 刘咏梅,成尚汶,谢虎.具有损失厌恶偏好零售商的供应链弹性数量契约[J]. 控制与决策,2012,27(7):975-982,990. Supply Chain Coordination with Quantity Flexibility Contract under the Scene of Multi-factor Disturbance LIU Lang1,2, SHI Wen-qiang3, FENG Liang-qing3 (1. School of Economic and Management, East China Jiaotong University,Nanchang 330013,China;2. Collaborative Innovation Center for Aviation Economy Development of Henan Province,Zhengzhou 450046, China;3.School of Economy and Management,Nanchang Hangkong University,Nanchang 330063,China) In this paper,inherent laws of two level supply chains being coordinated to deal with emergencies under multi-factor disturbance are explored. With regard to two situations of the market’s price,fixed and stochastic, the emergency quantity flexibility contract is used to find the optimal ordering and pricing strategy to realize the supply chain coordination. First, it is assumed that the elastic coefficients are constants and analyze the coordination problem under three scenes——when there is no emergency, there are emergencies making the price fluctuate and there are emergencies not making the price fluctuate;Second, the elastic coefficients are turned to variables to find the inherent constraints of achieving supply chain coordination; At last, examples are used to verify the emergency quantity flexibility contract with stochastic price above by simulation and analyze the influence of elastic coefficients’ change on related elements of the supply chain. The results indicate that: (1) the basic laws of realizing supply chain coordination under quantity flexibility contract are the same whenever the market price is fixed or stochastic. If only the wholesale price is adjusted appropriately, the uncoordinated supply chain can restore coordination; (2) when the contract elastic coefficientsαandβarefixed,thereexiststheexclusiveorderingandpricingstrategy;(3)Ifelasticcoefficientschange,theonlyorderingstrategyofthesupplychaindoesn’texist,buttheexclusivepurchasingstrategycanbeobtained.Thechangeofelasticcoefficientsatthetimeofcentralizeddecisionmakingexertnoinfluenceontheoptimalpurchasingquantity,supplyingquantity,theretailer’sexpectedgains,theexpectedgainsofthewholesupplychain,apartfromtheuplinkelasticitycoefficientαhavingeffectontheretailer’soptimalorderingquantity.Explanationoftheexampledata: (1)table1indicatesthatwhetherthemarketpriceisfixedorstochasticaswellasthedemandexpandsorshrinks,whenfelicitousamendmentismadetothewholesaleprice,theuncoordinatedsupplychaincanrestorecoordination; (2)table2-7illustratesthatwhenthemarketpriceisfixed,thechangeofupsideelasticcoefficientswillonlyaffecttheoptimalorderquantity(q*), having no effect on the retailer’s expected purchasesN(q)*, the supplier’s optimal supply ,the retailer’s expected profits and the proceeds of the whole supply chain regardless of the demand expanding or shrinking. Besides, the downside elastic coefficients’ change exerts no influence on the five elements referred above, and the optimal supply of the supplier is greater than the retailer’s expected purchasing quantities (i.e.Q*>N(q)*); (3)table 11-13 shows that the results obtained under stochastic price and shrunken demand is just the same as the results when the market price is fixed; (4) table 8-10 reveals elastic coefficientsαandβwillchangewhenthemarketpriceisstochasticandthedemandshrinks,andtheresultsareconsistentwithpreviousthreecasesexcepttheoptimalsupplybeingequaltotheretailer’sexpectedpurchasingquantity(i.e.Q*=N(q)*). Theoretical results are verified by case data. Inspiration is provided for the research that adopts other contracts to respond to price-stochastic or price-fixed emergencies, and foundation is laid for the further use of quantity flexibility contract to study more sophisticated emergency supply chain coordination problems under the condition of asymmetric information, different risk preferences of the participants and so on. stable price; random price; emergency quantity flexibility contract; supply chain coordination 1003-207(2016)07-0163-14 10.16381/j.cnki.issn1003-207x.2016.07.020 2014-07-31; 2015-02-18 国家自然科学基金资助项目(71562013,71162024,71362019);江西省教育厅科技项目(GJ14354) 刘浪(1973-),男(汉族),江西南昌人,华东交通大学经济管理学院教授,航空经济发展河南省协同创新中心研究员,硕士生导师,博士后,研究方向:应急供应链管理、应急物流,E-mail:liulang@ecjtu.edu.cn. F406.7 A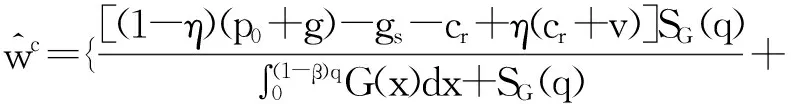
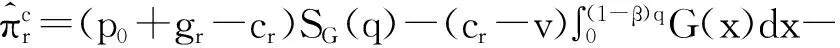



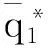
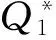
4 价格随机条件下应急数量弹性契约的供应链协调


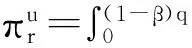



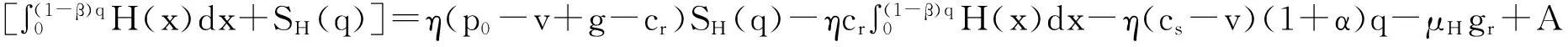
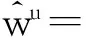

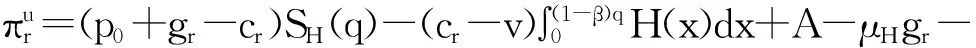
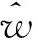

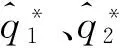
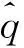
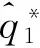



5 算例分析

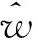











4 结语
